山区机场高填方边坡稳定性分析1)

冯 兴 姚仰平 张 健 张献民 黄 信

*(中国民航大学交通科学与工程学院，天津 300300)

†(北京航空航天大学交通科学与工程学院，北京 100191)

随着国民经济的发展，国家加大了机场建设投入，西部山区机场建设也发展迅速。由于山区地形复杂，为满足场地和净空条件，山区机场修建需要进行深挖高填，多为高填方工程，高填方填筑材料也多就地取材，多为土石混填材料。该类高填方机场相比于中东部平原机场，由于填方高，材料是力学特性复杂的土石混合填料，因此面临较多问题，其中高填方边坡稳定性问题是突出问题之一。如果能够解决高填方边坡稳定性问题，对整个机场实现绿色、低碳、高效和可持续发展的建设具有重要意义。许多学者对高填方边坡稳定性进行了研究，例如：陈涛等[1]对山区高填方机场地基变形和稳定性进行了研究，分析了路堤的沉降变形、侧向位移、塑性分布和路堤的稳定系数；臧亚君等[2]利用FLAC-3D 数值模拟对高填方地基的失稳模式进行了研究，并结合二维平衡计算对高填方体的稳定性进行了评价；陈金锋等[3]利用强度折减有限元法对昆明新机场高填方边坡稳定性进行了分析，并与简化Bishop方法的计算结果进行了对比；张新连等[4]研究了块碎石强度非线性对山区高填方边坡稳定性的影响，讨论了线性强度和非线性强度指标计算结果的差异。

目前边坡稳定性分析的方法主要分为极限平衡法和有限元（或有限差分）法两大类。极限平衡法[5-6]是原理最简单和基础的稳定性评价方法，但是对于复杂边坡工程，计算较困难，滑移面很难得到。随着数值计算技术的发展，有限元强度折减法由于保持了有限元在模拟复杂问题上的优点，而且概念明确、结果直观，不仅能较容易得到安全稳定系数，而且易得到边坡滑移面、应力、应变和位移场，因此，有限元强度折减法在工程中得到了越来越多的应用[7-9]。应用有限元强度折减法对高填方边坡稳定性能否进行合理的分析，一个关键的问题就是所采用的本构模型是否合理地反映了土体的力学特性[10-11]。文献[12-13]提出的统一硬化模型（unified hardening，UH）模型能够合理考虑土的复杂应力路径和应力历史对土体变形和强度的影响，它不仅能够描述正常固结土的特性，而且能够描述超固结土的硬化、软化、剪缩和剪胀等应力应变特性。笔者已经在UH 模型的基础上考虑了含石量，开发了考虑含石量的UH 土石混合料模型[14]，该模型可以合理反映土石混合料的应力应变特性，并且已经编制出了考虑含石量的UH 模型的材料子程序并进行了验证，实现了该模型在有限元中的应用。

本文主要是基于考虑含石量的UH 土石混合料模型，推导考虑含石量的UH 模型的强度折减参数，确定安全稳定系数的判断准则和计算流程，确定有限元分析时初始地应力平衡的方法；并采用有限元强度折减法，应用Mohr-Coulomb 模型和考虑含石量的UH 模型针对山区机场高填方边坡工程稳定性分别进行有限元分析，比较分析用两种模型计算的土体水平位移随边坡折减系数的变化曲线和不同填土高度的边坡安全稳定系数、边坡极限状态下土体水平位移、竖向位移和等效塑性应变云图，并分析不同含石量下的机场高填方边坡安全稳定系数，从而得到山区机场高填方边坡稳定性规律。

1 考虑含石量的UH 模型

1.1 屈服函数

在三维化的变换应力空间[15-17]中，考虑含石量的UH 模型的屈服函数[14]可表示为

1.2 弹塑性刚度矩阵

考虑含石量的UH 模型的弹塑性矩阵为

参照切线刚度矩阵对称化方法[18]对式（4）的弹塑性矩阵进行对称化处理，得到对称的弹塑性矩阵为

式中，Dep为弹塑性矩阵，De为弹性矩阵，σˆ为扩展空间滑动面（spatially mobilized plane，SMP）上的正应力，为变换应力空间扩展SMP 面上的正应力，为变换应力空间扩展SMP 面上的平均法向应力，ε为应变，r为对称转换系数，Ω为超固结系数。

2 考虑含石量的UH 模型的有限元强度折减方法

2.1 强度折减参数的确定

强度折减法可直接通过有限元分析获得安全系数，其概念明确，结果直观，工程上得到了广泛应用。建立在强度折减法基础上的边坡稳定分析的基本原理是将边坡强度参数黏聚力c和内摩擦角φ进行折减，得到新的强度参数ct和φt，其表达式[19]为

式中，Ft为折减系数，初始的Ft设置得足够小，但为大于1 的数，保证边坡的稳定性，然后慢慢加大Ft，当边坡达到极限平衡状态时，对应的Ft即为边坡的安全稳定系数。

式（8）计算用的土体本构模型是Mohr-Colomb 模型，对于考虑含石量的UH 模型，由于该模型中的参数[20]，所以可以通过折减c和M得到边坡的安全稳定系数。

将其代入式（8）得

因此，考虑含石量的UH 模型的强度折减参数可以表示为

其中，黏聚力c的公式[14]为

式中，cc为纯土的黏聚力，g(PR)公式为

内摩擦角φ的公式[14]为

以上，φc为纯土的内摩擦角，PR为含石量。

2.2 安全稳定系数的确定

有限元强度折减法一般采用3 种方式判定坡体是否达到极限破坏状态[21]：

（1）以塑性应变从边坡坡脚到坡顶是否贯通作为依据；

（2）数值计算不收敛作为边坡失稳的判断依据；

（3）绘制某一特征部位位移-折减系数曲线，曲线的拐点作为边坡失稳破坏的位置。

由于UH 模型是能够反映应变软化的弹塑性模型，所计算的土体单元均存在着塑性应变，所以判据（1）对UH 模型不适用，因此对于考虑含石量的UH 模型的强度折减法，主要结合判据（2）和判据（3）进行极限破坏状态的判断，即在数值计算不收敛的情况下，观测水平位移-折减系数曲线是否出现拐点，拐点所对应的折减系数即为安全稳定系数。安全稳定系数的计算流程如图1 所示。

图1 安全稳定系数的计算流程Fig.1 Calculation process of safety and stability factor

2.3 初始地应力平衡方法

在应用ABAQUS 软件，采用有限元强度折减法进行边坡稳定分析时，初始地应力场是影响边坡稳定性分析的重要因素之一，在稳定性计算中必须保持初始地应力的平衡，如果给定的初始应力场与自重载荷没有获得平衡，将可能导致非线性分析迭代的不收敛，得不到正确的结果，并且在ABAQUS 软件中应用考虑含石量的UH 模型材料子程序时，必须先给出整个土层所有单元高斯点初始应力σ0，形成弹塑性矩阵D0，从而形成初始刚度矩阵K0，然后才能再进行进一步的迭代计算。因此在应用考虑含石量的UH 模型对高填方边坡稳定性进行有限元分析时，首先要给定初始应力场，进行初始地应力的平衡。采取的方法如下。

（1）对整个土层材料模型采用弹性模型进行计算，然后将计算完成后的应力导出；

在命令行输入：

在后处理中，生成初始应力文件elastic.rpt，并通过Excel 将文件处理为elatic.csv 文件。

（2）将导出的初始应力导入到整个土层材料模型采用考虑含石量的UH 模型的有限元模型里，使内力和外力平衡，来获得较精确的未受干扰的原始状态。

在关键字文件中，添加：

3 山区机场高填方边坡稳定性分析

3.1 有限元计算模型及参数

参照康定机场AS5—AS5’剖面[22]建立山区机场高填方边坡的有限元模型，计算尺寸如图2 所示，路堤顶部宽度为15 m，坡度为1∶1.5，以每层填土高为10 m 向上填筑，共填筑三层，每层填土都建有一条宽度为2 m 的马道，地基土分为两层，下层地基为4.5 m，上层地基为5.5 m，地基土共10 m。边界条件为侧面采用法向约束，底边边界对其水平与垂直方向进行约束，地基顶面与路堤坡面为自由面。单元类型采用1 阶8 节点的三维实体单元(C3D8)，网格划分如图2 所示。整个土层的材料模型采用Mohr-Coulomb 模型和考虑含石量的UH 模型分别进行计算，各层土的计算参数参考相关文献假定[12]，如表1 和表2 所示，表中c为黏聚力，φ为内摩擦角，М为特征状态和临界状态下的应力比，λ 为等向压缩线的斜率，κ 为等向回弹线的斜率，e0为初始孔隙比，PR为含石量，E为弹性模量，ν为泊松比，γ 为重度。

表1 Mohr-Coulomb 模型材料参数Table 1 Soil parameters of Mohr-Coulomb model

表2 考虑含石量UH 模型材料参数Table 2 Soil parameters of UH model considering stone content

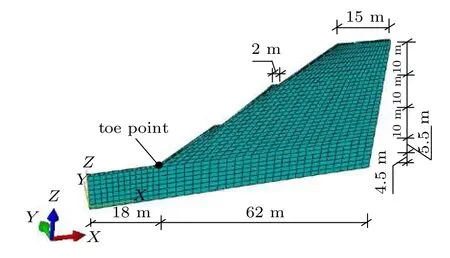
图2 有限元网格Fig.2 Meshes for finite element

3.2 结果分析

3.2.1 边坡安全稳定系数

图3 是应用Mohr-Coulomb 模型和考虑含石量的UH 模型对山区机场高填方边坡进行稳定性分析所得到的不同填土高度下坡脚点土体水平位移随边坡折减系数的变化曲线。Ft为折减系数，U1为水平位移。

图3 不同填土高度的坡脚点土体水平位移随折减系数的变化曲线Fig.3 Variation curves of soil horizontal displacement at slope toe point with reduction coefficient under different filling heights

由图3(a)可知，应用Mohr-Coulomb 模型进行计算所得到的位移曲线的变化趋势是：随着折减系数的增大，位移逐渐增大，当折减系数超过某一值（拐点）时，位移急剧增大，土体破坏。因此以位移曲线的拐点作为判定边坡失稳破坏的准则，则可以得到应用Mohr-Coulomb 模型计算所得到的安全稳定系数为：填土高度10 m 时位移曲线拐点为a点，对应的安全稳定系数为1.9；填土高度20 m 时位移曲线拐点为b点，对应的安全稳定系数为1.8；填土高度30 m 时位移曲线拐点为c，对应的安全稳定系数为1.6。

由图3(b)可知，应用考虑含石量的UH 模型进行计算所得到的位移曲线的变化趋势是：随着折减系数的增大，位移逐渐增大，当折减系数超过某一值（拐点）时，随折减系数增大而降低，土体破坏。因此，以位移曲线的拐点作为判定边坡失稳破坏的准则，可以得到不同填土高度时的边坡安全稳定系数：填土高度为10 m 时位移曲线拐点为a点，所对应的安全稳定系数为1.8；填土高度为20 m 时位移曲线拐点为b点，对应的安全稳定系数为1.6；填土高度为30 m 时位移曲线拐点为c，对应的安全稳定系数为1.1。

由图3 中考虑含石量的UH 模型计算曲线和Mohr-Coulomb 模型计算曲线比较可知，在拐点之前，二者计算趋势一致，都是随着折减系数增大，位移增大，但在拐点之后，考虑含石量的UH 模型计算的位移出现减小的趋势，而Mohr-Coulomb 模型计算的位移是急剧增大的趋势，那是由于考虑含石量的UH 模型能够反映土体在临界状态时的应变软化和土的剪胀作用，边坡在极限破坏状态时坡脚点土体出现了较强的应变软化，应变呈现剪胀；并且发现应用考虑含石量的UH模型计算的水平位移要比Mohr-Coulomb 模型计算的水平位移大，是由于考虑含石量的UH 模型考虑了含石量的影响，计算得到的上层较软地基上承受的应力要比Mohr-Coulomb 模型所计算的大，从而出现较大的水平位移；而且发现，对于Mohr-Coulomb 模型计算的位移曲线，随着填土高度的增大，边坡极限状态时所对应的水平位移也略微增大，变化不明显，而对于考虑含石量的UH 模型计算的位移曲线，可以清晰地看到填土高度20 m 的边坡极限状态时所对应的水平位移比填土高度为10 m 时所对应的水平位移大，但是填土高度30 m 的边坡极限状态时所对应的水平位移反而小，说明了考虑含石量的UH 模型在计算填方较高边坡时在坡脚土体水平位移较小时就出现了边坡的失稳。

图4 是应用Mohr-Coulomb 模型和考虑含石量的UH 模型计算的机场高填方边坡安全稳定系数随填方高度的变化曲线。由图4 可知，应用两种模型计算的安全稳定系数都是随着填方高度的增加呈减小趋势，并且发现应用考虑含石量的UH 模型所得到的安全稳定系数要比应用Mohr-Coulomb 模型计算所得到的安全稳定系数要小，而且填方高度越大，应用UH 模型所计算的安全稳定系数比Mohr-Coulomb 模型计算的越小，可见，在高填方边坡分析中，应用考虑含石量的UH 模型计算的安全稳定系数相比Mohr-Coulomb模型更加安全可靠。

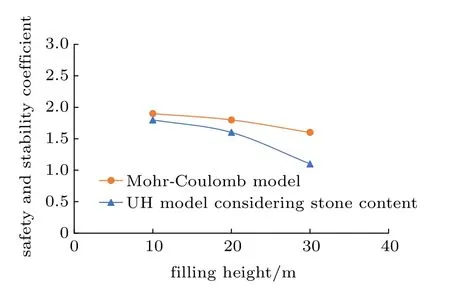
图4 不同填土高度的机场高填方边坡安全稳定系数Fig.4 Safety and stability coefficients of airport high fill slope with different filling heights

对考虑含石量的UH 模型中的参数含石量PR进行敏感性分析，针对填土高度为30 m 的机场高填方边坡进行有限元分析，以表2 中的材料参数作为模型参数标准，变化3 个填土层和下层地基的参数含石量PR，分别为PR=40%，PR=50%，PR=60%，采用强度折减法计算参数含石量PR变化后的安全稳定系数，研究参数变化对安全稳定系数影响程度的大小，来确定参数的敏感程度。图5 是所得到的不同含石量下高填方边坡坡脚点土体水平位移随边坡折减系数的变化曲线。由图5可知，含石量PR=40%的位移曲线拐点为a点，对应的安全稳定系数为1.1，含石量PR=50%的位移曲线拐点为b点，对应的安全稳定系数为1.3，含石量PR=60%的位移曲线拐点为c点，对应的安全稳定系数为1.6。可见，含石量PR不同，安全稳定系数也不同，含石量PR对高填方边坡的安全稳定系数有着较大的影响。图6 是机场高填方边坡含石量和安全稳定系数的关系曲线，由图6 可知，随着含石量的增大，安全稳定系数呈现增大趋势，在含石量为40%～60%这个范围内，基本呈等比例的增长趋势。

图5 不同含石量的高填方边坡坡脚点土体水平位移随折减系数的变化曲线Fig.5 Variation curves of soil horizontal displacement at high fill slope toe point with reduction coefficient under different stone content

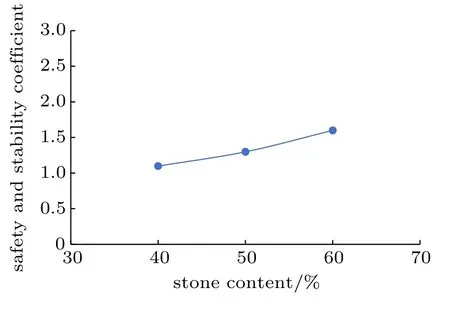
图6 机场高填方边坡含石量和安全稳定系数的关系曲线Fig.6 Relationship curve between stone content and safety stability coefficient of airport high fill slope

3.2.2 位移分析

图7 为应用Mohr-Coulomb 模型和考虑含石量的UH 模型计算的不同填土高度的边坡极限状态下土体水平位移云图，图中U1为水平位移。由图7 可知，应用两种模型计算的土体水平位移云图都表明在不同填土高度下，边坡在极限失稳状态下，近似的圆弧滑动破坏为高填方边坡的主要破坏形式，并且发现随着填土高度的增加，滑动破坏的区域范围也逐渐增大，最大可能滑裂面向边坡内部逐渐扩展。不同的是，Mohr-Coulomb模型计算的水平位移云图中，在坡脚处的水平位移最大，其范围由坡脚向边坡中部延伸，而考虑含石量的UH 模型计算的水平位移云图中，同样是在靠向坡脚处的水平位移最大，但其范围是由坡脚向坡面延伸。

图7 不同填土高度的边坡极限状态下土体水平位移云图Fig.7 Cloud charts of horizontal displacement of soil under limit state of slope with different filling heights

图8 为应用Mohr-Coulomb 模型和考虑含石量的UH 模型计算的不同填土高度下边坡极限状态下土体竖向位移云图，图中U3为竖向位移。由图8可知，考虑含石量的UH 模型计算的竖向位移云图中，填土高度在10 m，20 m 和30 m 时，边坡在极限失稳状态下，坡顶的竖向位移最大，远离坡顶，竖向位移逐渐减小，在坡脚处，产生了正向的竖向位移，土体出现了隆起现象。这是由于在高填方工程中填方量高，填方载荷大，作用于较软弱地基上，导致坡底土体出现了隆起现象，在施工中要注意在坡底采取有效措施来防治灾害的发生。而应用Mohr-Coulomb 模型计算的竖向位移云图中，基本和考虑含石量的UH 模型计算的规律相同，但是填土高度为10 m 时，坡脚的土体没有出现正向位移。

图8 不同填土高度的边坡极限状态下土体竖向位移云图Fig.8 Cloud charts of vertical displacement of soil under limit state of slope with different fill heights

3.2.3 边坡应变分析

图9 为应用Mohr-Coulomb 模型和考虑含石量的UH 模型计算的不同填土高度的边坡极限状态下土体等效塑性应变云图，图中PEMAG 和SDV17 均为等效塑性应变。由图9 可知，在填土高度为10 m 时，考虑含石量的UH 模型计算的土体等效塑性应变云图中，边坡在极限失稳状态下，边坡的塑性区域由坡脚开始，逐渐向坡顶延伸，形成了一圆弧滑动带。而Mohr-Coulomb模型计算的土体等效塑性应变云图中，塑性区也是由坡脚向坡顶延伸，但是在坡脚靠向边坡中部的软土地基区也出现了较大的塑性区。同样，在填土高度为20 m 时，两种模型计算的等效塑性应变云图规律和填土高度10 m 时类似。在填土高度为30 m 时，Mohr-Coulomb 模型计算的土体等效塑性应变云图中，仍然是塑性区由坡脚向坡顶延伸，但是滑动带偏于狭窄，而考虑含石量的UH 模型计算的土体等效塑性应变云图中，塑性区也是由坡脚向坡顶延伸，但是滑动带变宽，滑动破坏的范围变大。

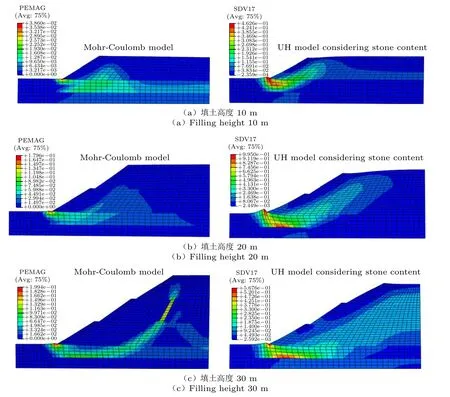
图9 不同填土高度的边坡极限状态下土体等效塑性应变云图Fig.9 Cloud charts of equivalent plastic strain of soil under limit state of slope with different fill heights

4 结论

(1)确定了考虑含石量的UH 土石混合料本构模型的折减参数M，c的公式，通过对M和c进行折减，且通过判断水平位移-折减系数曲线是否出现拐点作为应用考虑含石量的UH 模型进行边坡失稳分析的判断准则，并设置合适的初始应力场，可以方便地应用有限元强度折减法对山区机场高填方边坡稳定性进行分析。

(2)通过应用Mohr-Coulomb 模型和考虑含石量的UH 模型对山区机场高填方边坡工程进行有限元分析，得出随着填土高度的增大，安全稳定系数呈现减小趋势，随着含石量的增大，安全稳定系数呈现增大趋势；并且通过两种模型计算结果的比较可知，应用考虑含石量的UH 模型能够反映边坡土体在临界状态时的应变软化和剪胀现象，并且所计算的安全稳定系数比Mohr-Coulomb模型计算的小，而且随着填土高度的增大，这种情况更加明显，说明了应用考虑含石量的UH 模型分析高填方边坡稳定性相比Mohr-Coulomb 模型更加安全可靠。

(3)通过对应用Mohr-Coulomb 模型和考虑含石量的UH 模型计算的山区机场高填方边坡在极限破坏状态下的位移和应变分析，得出近似的圆弧滑动破坏为高填方边坡的主要破坏形式，并且由考虑含石量的UH 模型计算的塑性应变云图中得出随着填土高度的增大，滑动破坏的范围也越大，而且坡脚处为正向的竖向位移，土体出现了隆起现象。