钢制管片二次衬砌加固效果数值分析

2024-03-16郭泽宇

科学技术创新 2024年6期

唐懿，郭泽宇

（中交第二公路勘察设计研究院有限公司，湖北武汉）

引言

日本自昭和二十八年“电信电话扩充的第一个五年计划”，进行了大规模的电气通讯隧道建设。如今，NTT 和东电的通讯隧道大多数已经使用超过40 年，逼近50 年的设计年限了[1]。伴随着长期使用，隧道老旧化和损坏的问题不断发生。然而，以东京为例，浅层地下空间的利用已经饱和了，要建设新的隧道只能在大深度的地层实施，这需要高额的建设费用[2]。再者，地下建筑相较地上建筑，拆除难度大。因此，对于加固和修补既有隧道以延长其使用寿命的研究很有必要。

现存的铺设了二次衬砌的盾构隧道以钢制管片隧道为主，二次衬砌在设计时仅作为防水防腐蚀的非结构构造。合理设计二次衬砌并考虑其加固效果可以有效提高结构的使用寿命。但现存的关于钢制管片二次衬砌加固效果的论文和研究较少。本文以某钢制管片隧道为例，评价了二次衬砌对于盾构隧道的加固效果，可为相关工程提供参考。

1 数值模型与计算参数

1.1 研究方法

对于钢制管片的数值解析，一般采用梁-弹簧模型或者均值圆环法的线性解析方法或非线性解析方法[3-4]。本文通过建立二维梁-弹簧模型验证了三维非线性FEM 模型的合理性并对其进行优化，之后使用非线性FEM 模型求解了“仅设置一次衬砌”和“设置一次衬砌+二次衬砌”工况下盾构隧道结构的承载能力极限状态。

1.2 模型介绍

仅设置一次衬砌条件下，二维模型采用Moleman软件计算，模型为梁-弹簧模型，块间弹簧采用回转弹簧，环间弹簧采用拉压弹簧。共建立三环模型，前后环为半环，中间环为完整圆环。三维模型采用Diana 有限元软件计算，模型采用实体，建立六个完整圆环进行计算。

在考虑二次衬砌的条件下，二维模型一次衬砌与二次衬砌的连接采用拉压弹簧，二次衬砌同样等效为梁单元进行建模，一次衬砌模型不变。三维模型的二次衬砌采用实体进行模拟，二次衬砌与一次衬砌的连接采用界面进行模拟，一次衬砌模型不变，如图1 所示。

图1 “设置一次衬砌+二次衬砌”结构计算模型

1.3 计算参数

本次采用的模型外径3 150 mm，内径2 892 mm，二次衬砌厚度175 mm，单节管片长900 mm，错缝角度为49.655°。

混凝土材料采用总应变裂缝模型。混凝土抗拉本构采用hordijk 抗拉本构[5]，抗压本构采用抛物线抗压本构[6]。钢材采用Von Mises 屈服准则。在非线性FEM数值解析模型中，通过界面模型来模拟环间接头、块间接头及地基弹簧。环间接头采用线弹性三维界面。块间接头，采用非线弹性界面。地基弹簧则采用仅受压的非线弹性界面。

二次衬砌与一次衬砌间的连接，本研究采用coulomb 摩擦模型的面界面模拟。最初的黏着强度为6.00 N/mm2[7]。

1.4 加载方式

为求得三维非线性FEM 模型的结构极限承载力能力，在荷载达到设计荷载之前，水平方向和垂直方向的分布荷载为0.1 倍的设计荷载逐步递增；到达设计荷载之后，考虑到荷载最不利情况，只有垂直方向荷载逐步递增，直至达到材料的极限状态。

2 解析结果

2.1 三维非线性FEM 模型可靠性验证

为了更好地研究钢制管片的截面力，为了保证模型的准确性，首先使用梁-弹簧模型进行分析，然后通过非线性有限元分析再次计算截面力。在比较了弹簧-弹簧模型与三维模型的截面力差异后，分析原因并进一步对三维模型进行修改。

2.1.1 “仅设置一次衬砌”模型

如图2 所示为“仅设置一次衬砌”工况下的计算结果，由此可知：

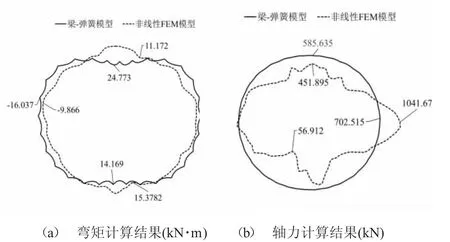
图2 “仅设置一次衬砌”二维模型与三维模型计算结果比较

两个模型的最大正弯矩和最大负弯矩发生的位置相同，但是三维模型的弯矩值要比二维模型的小，这是两个模型的材料模型不一样以及接头部位的模拟手段不一样导致的；相应的，轴力的不同是接头部分的模型不一样导致。三维模型在块间接头部位有应力集中现象发生。此外，由于三维非线性有限元模型对承重作用相对较弱的外壳板进行建模，因此在分析过程中对纵向横截面方向占据较大面积的外壳板施加了不可忽视的载荷。

总而言之，两者整体趋势为几乎一致。因此，非线性有限元模型不存在重大的结构问题，可以继续分析其极限承载能力。

2.1.2 “设置一次衬砌+二次衬砌”模型

如图3 所示为“设置一次衬砌+二次衬砌”工况下的计算结果，由此可知：

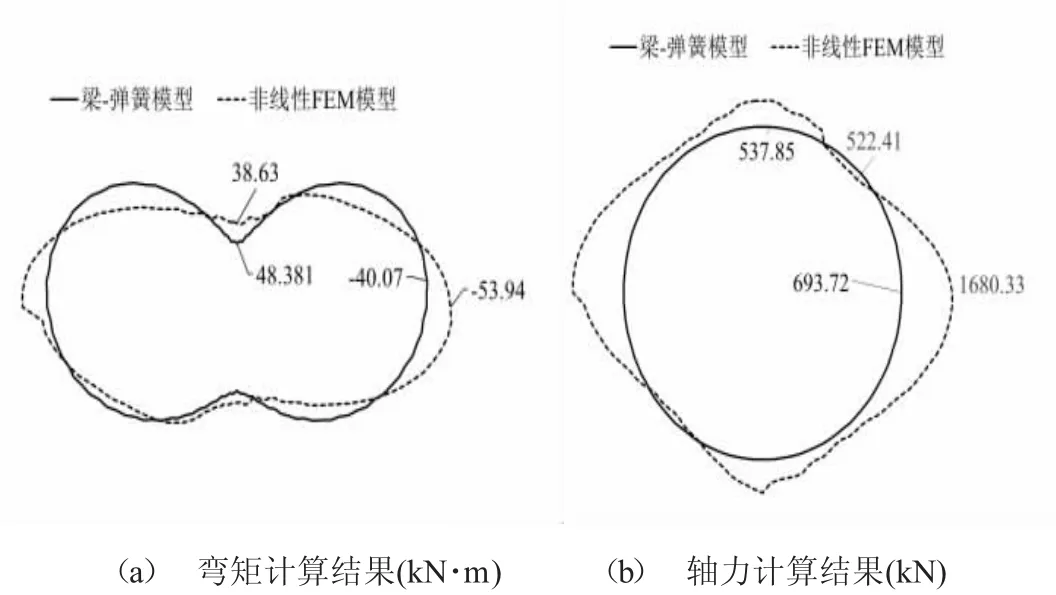
图3 “一次衬砌+二次衬砌”二维模型与三维模型计算结果比较

从弯矩结果来看，两个模型中，三维模型和二维模型在一次衬砌的结果上有较大差别，该原因与“仅设置一次衬砌”工况类似，缘于对于接头的计算模型的差异，总体的弯矩结果来看没有太大的差异。从轴力结果来看，差异产生的是二维模型没有考虑纵肋分担荷载的能力，而在三维模型中不仅考虑了纵肋的载荷能力还考虑了纵肋与二衬之间的相互作用。

因此，三维模型在构造上没有问题，可以继续进行承载能力的解析。

轴力及弯矩比较见表1。

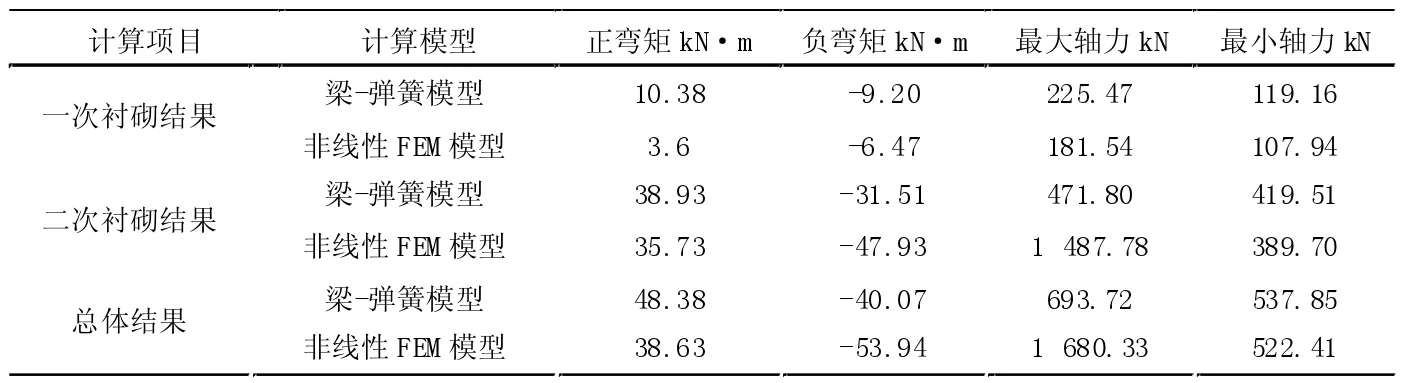
表1 轴力及弯矩比较

2.2 结构极限承载能力分析

由2.1 节中模型结果可知：盾构隧道在水平以及竖直方向上的变形、轴力、弯矩值都是极大值。因此在对模型进行承载能力监测时：（1）对于变形的监测选择内空的上下左右四个点。（2）对于应力的监测选用上一章节设计荷载下模型弯矩最大值发生位置。

2.2.1 隧道净空变形分析

如图4 所示为“仅设置一次衬砌”工况与“设置一次衬砌+二次衬砌”工况下隧道竖直净空变形与所受荷载的关系，图5 为隧道水平净空变形与所受荷载的关系。

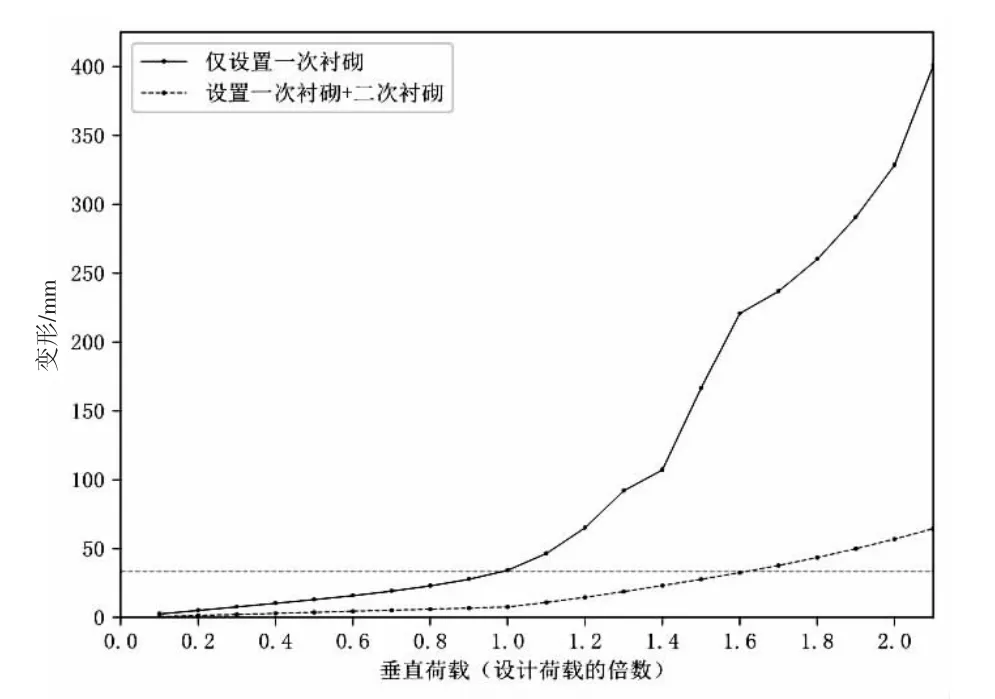
图4 隧道竖直变形与荷载关系

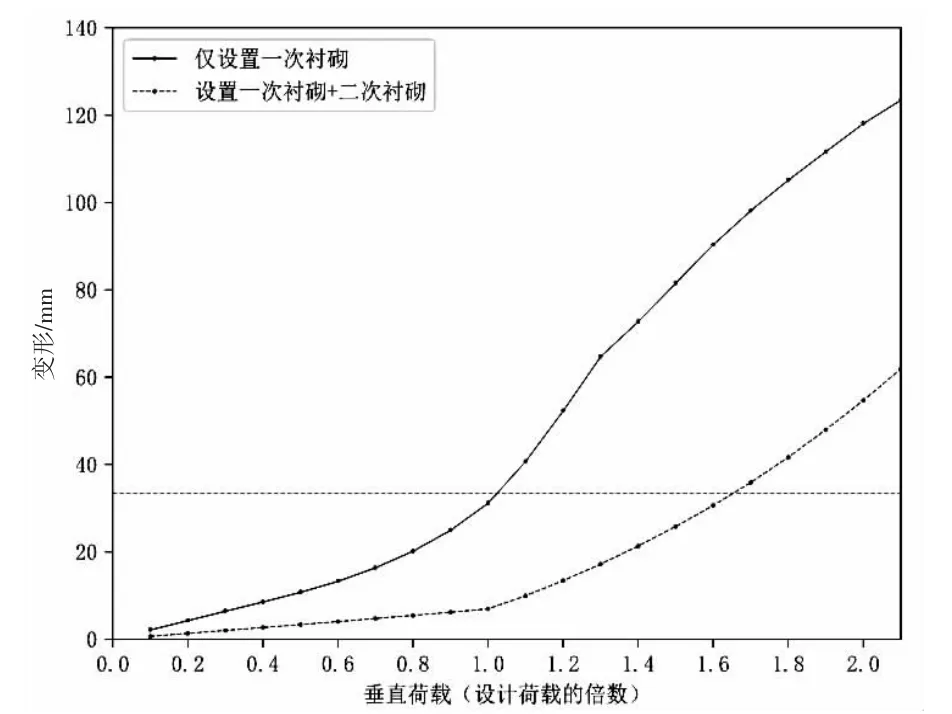
图5 隧道水平变形与荷载关系

根据日本规范标准以及以前的案例，输电管道这种小直径隧道的正常使用极限值为隧道直径的1/100～1/150 倍左右[3]，对于本次研究对象为33.5 mm。

由图4、图5 可知，当仅设置一次衬砌时，在设计荷载即1.0 倍垂直荷载作用下，结构的竖直和水平净空变形接近于虚线的正常使用状态的极限变形值。当设置了一次衬砌+二次衬砌时，在设计荷载下，结构的竖向净空变形为6.94 mm，水平净空变形为7.69 mm，远小于极限变形值。竖向变形和横向变形达到结构极限变形值时，结构承受的荷载约为1.62 倍的设计荷载。

隧道净空的变形在达到设计荷载之前，水平向与竖直向较为相同，这是因为此时的结构尚在其弹性变形范围内，而后在结构塑性范围内，隧道净空的变形急剧上升，且由于竖向应力差值大于水平应力差值，因此垂直净空变形变化幅度大于水平净空变化幅度。

2.2.2 隧道衬砌应力分析

如图6 所示为“仅设置一次衬砌”工况与“设置一次衬砌+二次衬砌”工况下隧道衬砌应力与结构所受荷载的关系曲线。

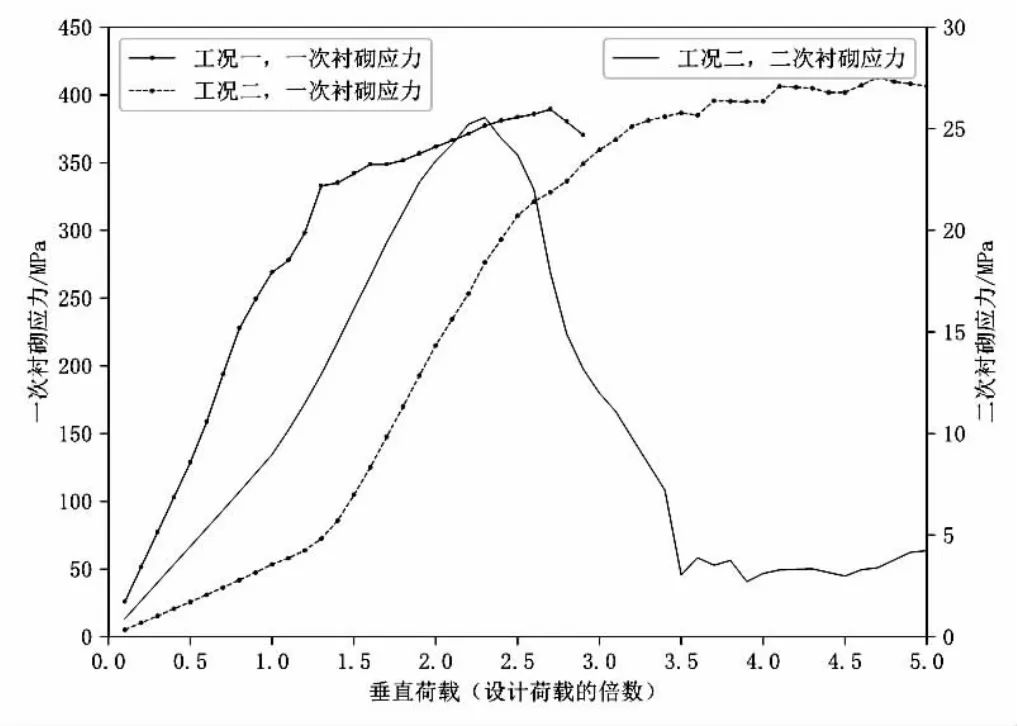
图6 隧道衬砌应力与荷载关系

由图6 可知，一次衬砌的应力曲线与钢材的本构模型相符，二次衬砌的应力曲线与混凝土的本构模型相符，验证了试验加载的有效性。

当仅设置一次衬砌时，结构在1.0 倍设计荷载下，材料应力约为269 MPa，结构在1.2 倍的设计荷载下，材料趋于屈服状态，应力约为297 MPa。

当设置一次衬砌+二次衬砌时，结构在1.0 倍设计荷载下，一次衬砌应力仅为53 MPa，二次衬砌应力约9 MPa，二次衬砌为一次衬砌分担了大部分的荷载。在超过设计荷载后，二次衬砌逐步失去承载能力，转而由一次衬砌承担荷载，垂直荷载提升至1.3 倍设计荷载后，一次衬砌应力急剧增大。垂直荷载为2.1 倍设计荷载时，混凝土应力接近其抗压强度。垂直荷载为2.4倍设计荷载时，一次衬砌材料趋于屈服。因此可以认为考虑二衬的情况下，2.1 倍的荷载设计值是该结构的承载能力极限值。