平行共轴圆线圈互感系数的测量与计算

张克生

（江苏安全技术职业学院，江苏 徐州）

引言

互感系数简称互感，其单位与自感相同，为亨利，简称亨。它的大小取决于两个线圈的几何形状、大小、相对位置、各自的匝数以及他们周围介质的磁导率。互感系数的计算一般都比较复杂，常通过实验方法测定。目前已有不少学者对不同几何形状线圈的互感系数进行理论计算和实验测量，其中吴德会等[1]给出了任意两个平面多边形螺线线圈间互感系数的解析模型，隗群梅[2]采用LCR 数字电桥测量出同轴等大圆线圈互感系数，邝向军等[3]根据诺依曼公式计算两共轴矩形载流线圈间的互感系数，龚禔[4]给出两共轴圆线圈间互感系数的简便计算方法，岑敏锐[5]给出两个同轴等大方形线圈的互感系数的近似解析式，张星辉等[6]给出了任意两共轴圆线圈间的互感系数及磁感线的分布。本文在前期研究[7]的基础上，通过理论模型与数值模拟，计算出两平行共轴矩形截面圆线圈的互感系数。利用常见的普通物理实验器材，采用三种实验方法测量互感系数，可加深对互感系数、感抗、阻抗等概念的理解，再将实验值与理论计算值进行比较，并进一步分析两平行共轴圆线圈耦合系数随距离的变化关系，对设计互感线圈能提供理论参考。

1 两平行共轴圆线圈的互感系数

如图1 所示，两平行共轴圆线圈L1和L2的半径为r1、r2，两圆线圈之间的距离为d，根据诺依曼公式，两平行同轴圆线圈的互感系数为

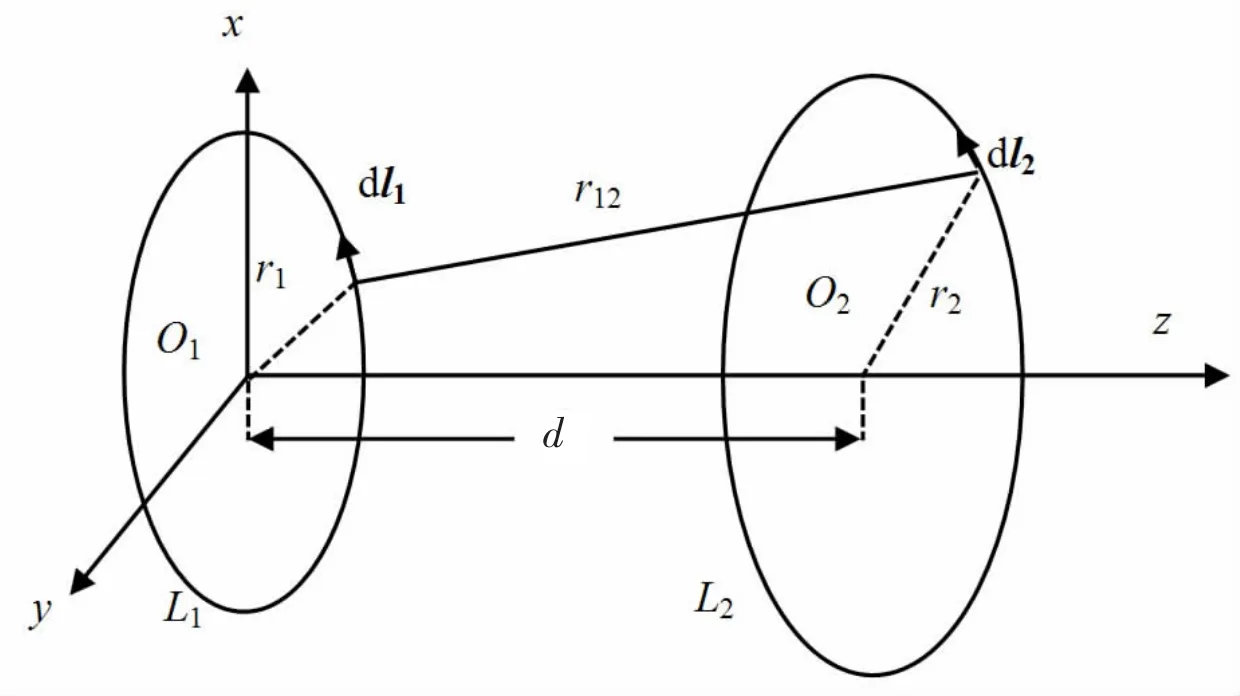
图1 两平行共轴圆线圈

式中:r12为圆线圈上两微元 dl与 dl之间的距离，利用坐标变换，式(1)可化简为[8]

2 线圈模型与数值计算

如图2 所示的两平行共轴矩形截面圆线圈，其实物原型为杭州精科Fb516 型磁场描绘仪中的亥姆霍兹线圈。根据实际线圈的几何尺寸及绕制方式，将左右两个圆线圈分别看成独立的单匝线圈密绕而成。线圈平均半径R 为10 cm，线圈导线的半径a 为0.3 mm，每层10 匝，共10 层密绕，总匝数为100 匝。每个圆线圈可以看成是100 个独立的单匝圆线圈平行共轴紧密排列，整个线圈绕组的截面为0.6 cm×0.6 cm的正方形。以两圆线圈的中心轴线为坐标轴，几何中心位置为坐标原点，两组线圈之间的距离为d。利用诺依曼公式和数值积分软件，由式(2)可以计算左右两侧任意两个单匝线圈之间的互感系数，然后对所有的互感系数累加求和，即可得到两平行共轴矩形截面圆线圈的互感系数M。

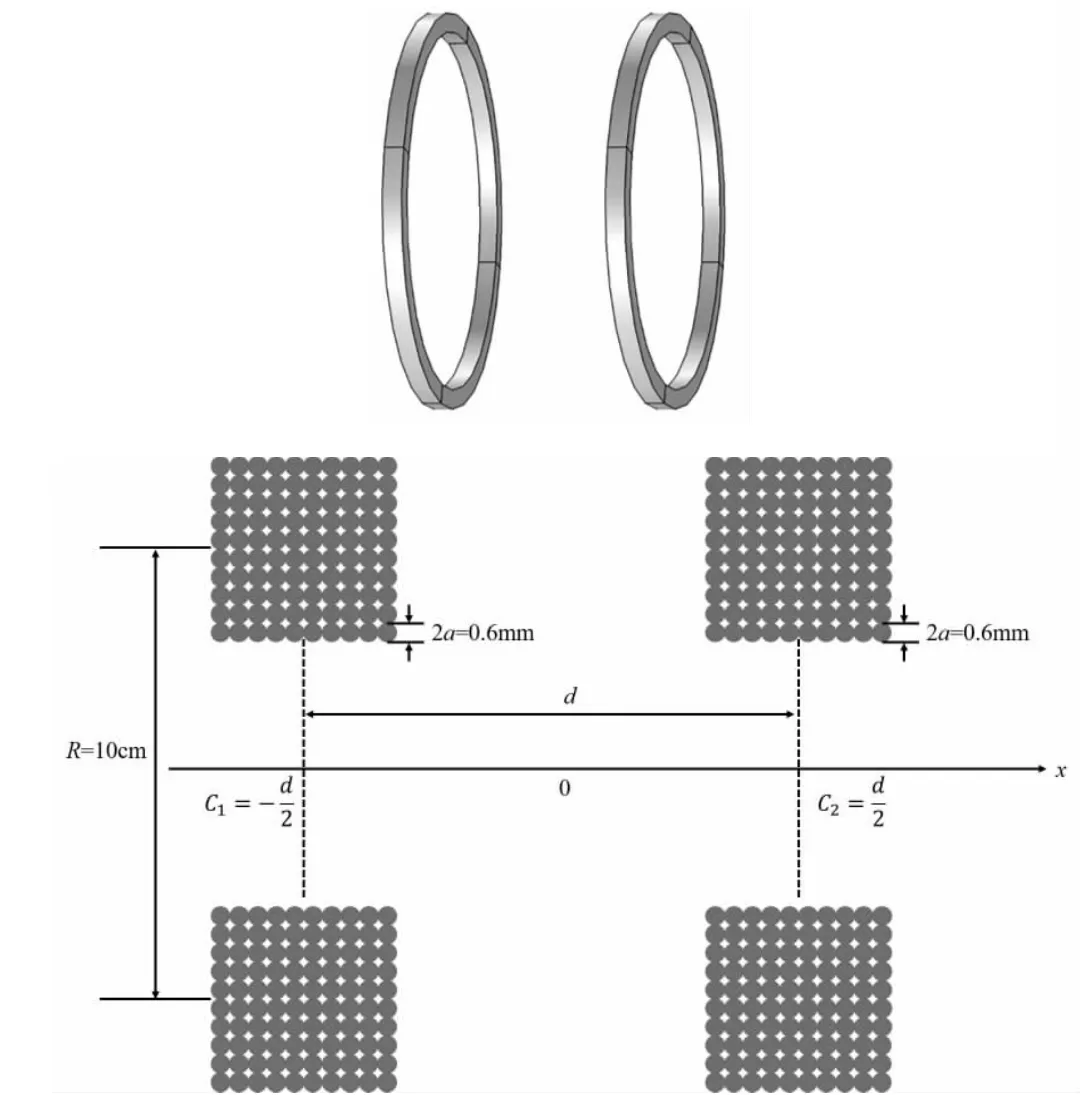
图2 两平行共轴矩形截面圆线圈及其截面示意

3 实验测量

3.1 电感表测量互感系数

两组线圈自身的电感分别为L1和L2，互感为M12。如图3 所示，当两组线圈顺接时，总电感为L顺，两组线圈逆接，总电感为L逆。

图3 两线圈顺接和逆接示意

其中：L顺=L1+L2+ 2M，L=L1+L2-2M，可得

如图4 所示，将两组平行共轴圆线圈顺接或逆接，利用电感表测量不同距离的总自感系数L，利用式(3)可计算出互感系数M。

图4 电感表测量线圈电感系数实物

3.2 伏安法测量互感系数

由于实际线圈自身具有一定的直流电阻，同时在交流电路中具有感抗，在测量其电感系数前，需要精确测量两圆线圈串联时直流电阻R。对于实际使用的线圈，为了测量准确起见，可以采用常用的电桥法进行测量，经过测量得到串联时两线圈的总电阻R 为8.92 Ω。如图5 所示，将两线圈顺接或逆接后两端接入信号源，信号选择正弦交流信号，频率f 设置为400 Hz，利用数字万用表交流电压档测量电压有效值U，交流电流档测量回路中的电流有效值I，当整个RL 电路达到稳态时，根据U、I 以及信号源的频率f，可按式(4)计算两线圈顺接或逆接后电感系数L。

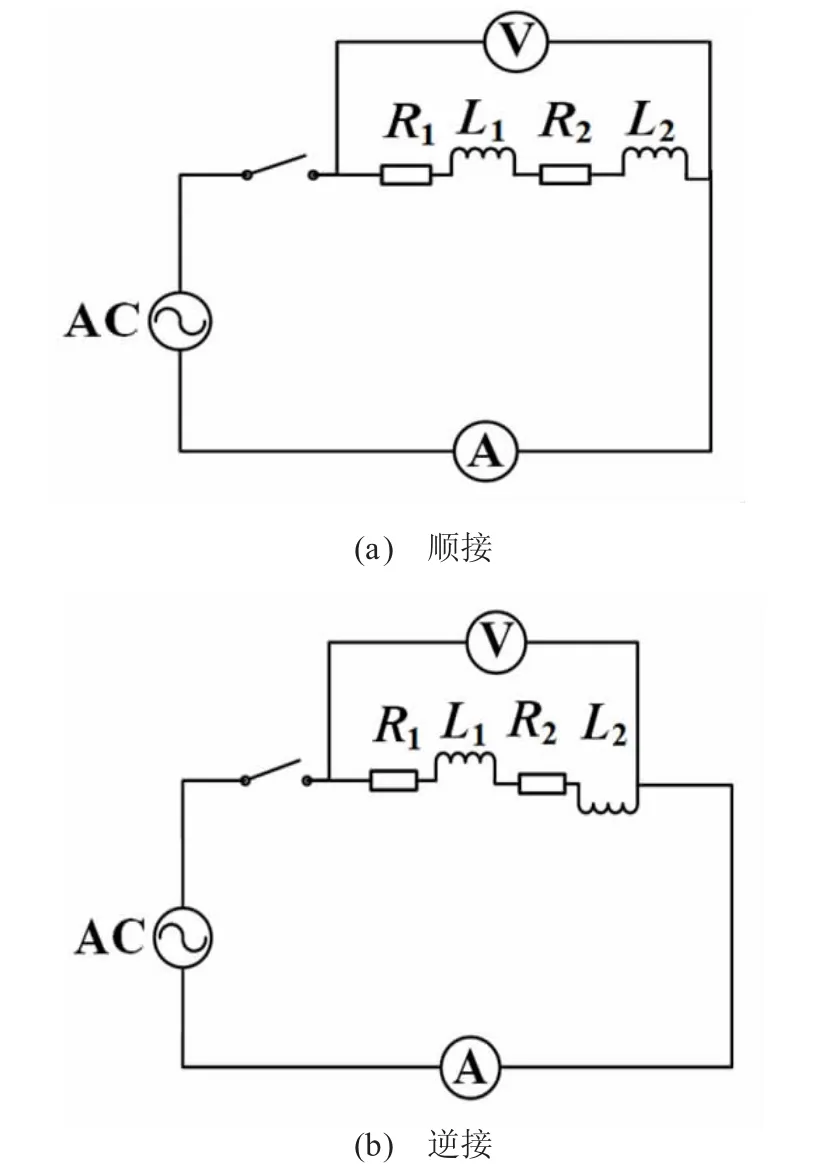
图5 伏安法测互感系数电路

再根据式(3)计算出互感系数M。

3.3 电磁感应法测量互感系数

如图6 所示，将两圆线圈平行共轴放置，距离为d，其中线圈1 接入信号源，输出信号选择正弦交流信号，频率f 设置为400 Hz，串联一台数字万用表，用交流电流档测电流有效值I，另一台数字万用表交流电压档测量线圈2 两端电压有效值U。当整个电路稳定时，左侧回路的正弦交流电流在右侧线圈两端感应出正弦交流电压，根据电磁感应定律，可得

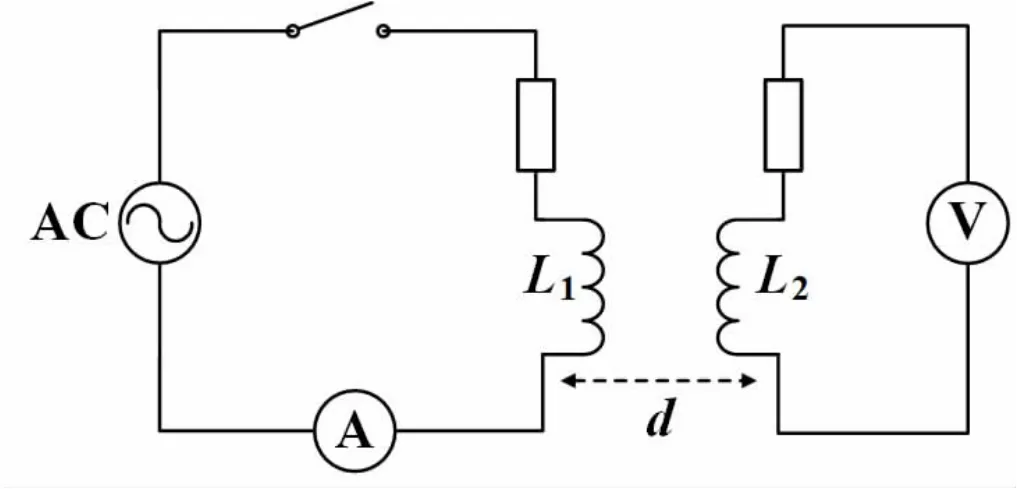
图6 感应法测互感系数电路

将两万用表测量出的U、I 以及信号源的频率f 带入式(5)，即可计算出两平行共轴圆线圈在距离d 处的互感系数M。

4 结果分析与总结

将理论计算与实验测量结果进行比较，数据如表1 所示。实验的误差主要来自于仪器仪表(数字万用表、电感表、信号源等)自身的误差，连接导线的电阻以及接线柱的接触电阻等。实验值与计算值之间的相对误差均低于5%，两者十分吻合，彼此相互验证。

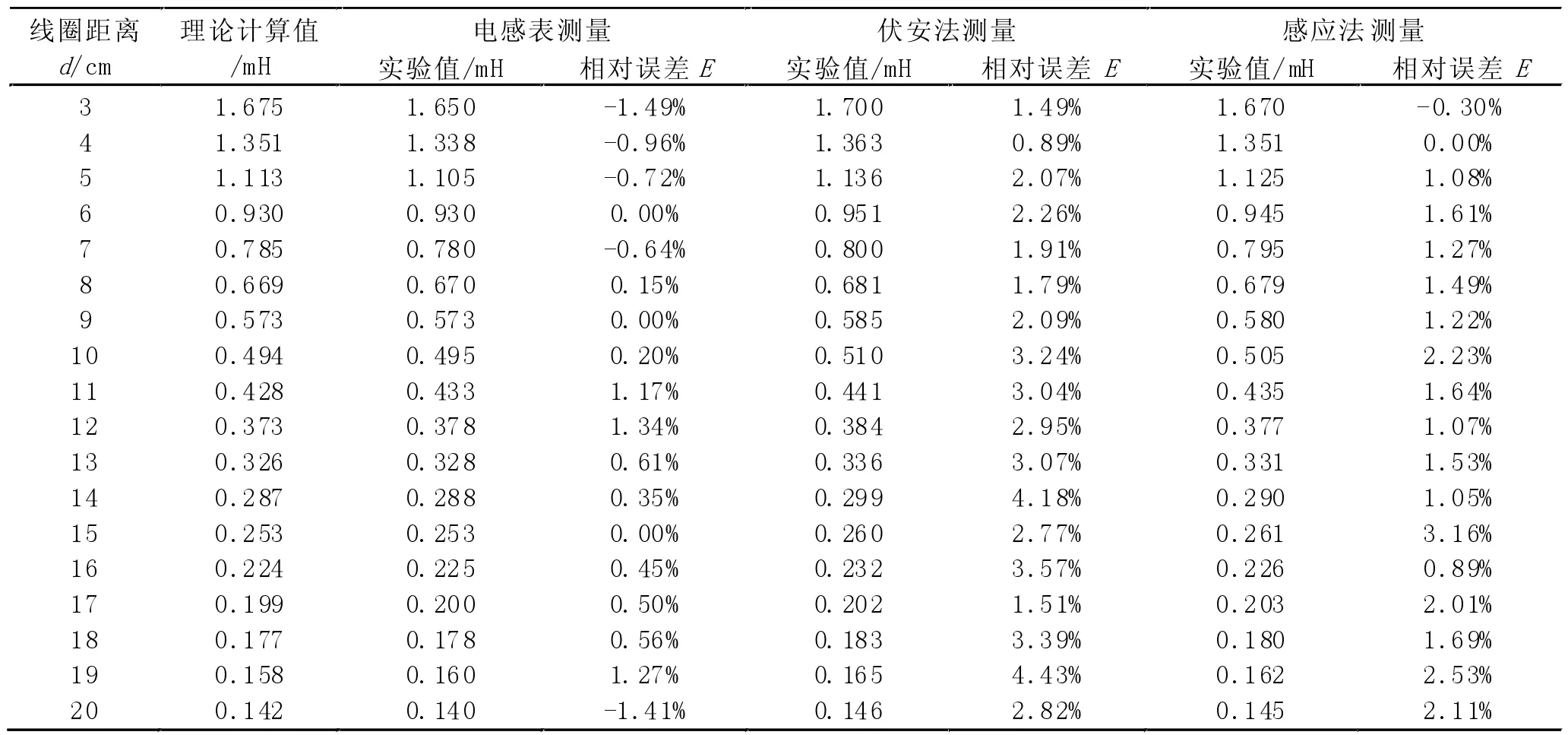
表1 理论计算与实验测量结果对比

根据互感耦合系数K 的定义

利用电感表直接测得单个圆线圈的自感系数L1=L2=4.66 mH，根据(6)式即可得到两平行共轴圆线圈的耦合系数M。互感系数M 与耦合系数K 随两线圈之间距离d 的变化曲线如图7 所示，由图可知实验曲线与理论计算曲线几乎重合。当d=R=10 cm，即两线圈之间的距离刚好等于线圈时，两线圈组成亥姆赫兹线圈，由计算数据可知此处两线圈的互感耦合系数约为0.1。

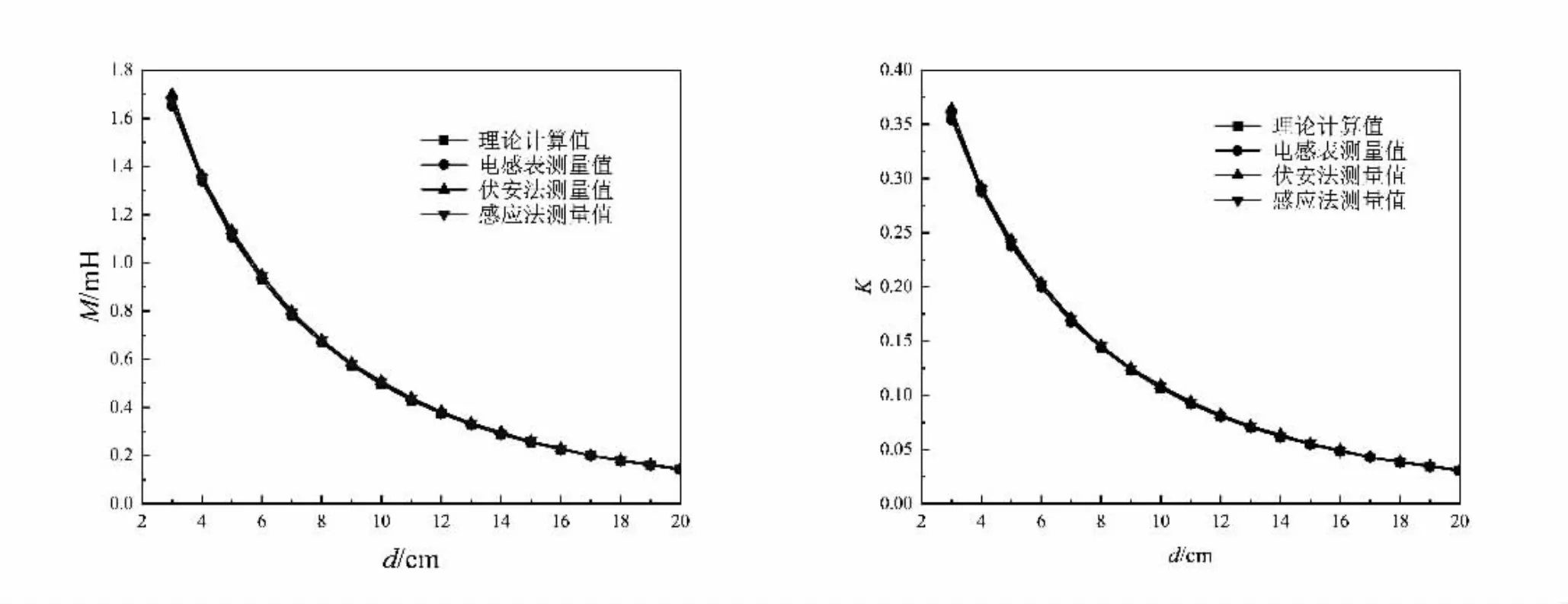
图7 互感系数与耦合系数随两线圈之间距离的变化曲线

本文利用大学物理实验常用的实验器材，采用三种实验方法测量了平行共轴圆线圈的互感系数，实验过程中可以加深相关物理概念的理解，通过实验测量结果与理论计算值进行比较，实验与理论计算模型相互验证，并进一步分析耦合系数随距离的变化关系，对设计互感线圈能提供理论参考。