黄渤海海区风速推算方法及效果评估*
2024-03-15曲巧娜
曲巧娜 吴 炜
1 山东省气象防灾减灾重点实验室,济南 250031
2 山东省气象科学研究所,济南 250031
提 要:为了弥补海上风场监测数据不足,提高对黄渤海海上风场监测能力,针对不同大气环流形势,基于较为稳定的74个沿海和海岛站等陆基站2017—2020年风场观测资料,以及同时段具有一定连续性的21个浮标站和船舶站等海基站观测数据,采用多元线性回归方法,建立由陆基站推算海区风速的模型。利用2021年实况资料对推算结果进行检验评估。结果表明:分别针对全部风力等级和6级及以上大风建立的风速推算模型(以下分别简称CM模型和HM模型)均具有较高的可靠性,其中HM模型对大风推算的准确率更高;8种天气类型中共5种类型发生大风的概率高于60%,其中对西北高东南低类型的推算效果最好,对西高东低型、西南高东北低型和西北低东南高型的6~7级大风推算效果较好,对8级及以上大风的推算效果略差;不同海区大风的推算结果中,对黄渤海大部分海区推算的风速略偏小,仅对渤海西南部海区的部分站点推算的风速略偏大;对黄海北部海区风速推算的平均绝对误差最小(0.95 m·s-1),对其他海区风速推算的平均绝对误差在1.32~1.70 m·s-1;在海区观测不连续、不稳定的情况下,推算的风速能够对海上风场资料进行有效的补充。该推算方法易于业务化应用,可随不同海区观测资料的增加而进一步优化,对海洋观测布局设计也有一定的参考作用。
引 言
黄渤海海区属于温带海洋性气候,是恶劣的海洋天气及衍生的海洋灾害频发的海区(解以扬等,2014),其中海上大风是引发海难事故最活跃的风险因子,同时黄渤海海区是中国对外贸易往来的重要通道之一,海上经济活动活跃,精细化大风预报服务是海洋经济安全高效发展的重要保障,海洋防灾减灾和气象预报预警业务对实况资料的需求十分迫切。然而,广阔的海面上气象观测资料稀少。少量的浮标站、船舶站可直接获取海面风场资料,但保障较差;借助卫星可获得大范围风场反演资料,但时间不连续且易受天气影响,提高监测能力一直是研究的目标之一。实际业务中,沿海和海岛等陆基站资料的连续性好、质量较高,是海上大风的重要参考,在忽略海陆差异的前提下,常被作为邻近海区的“指标站”;另外,数值预报产品及再分析资料也是一个重要的参考,但是模式对于海区风的预报误差较大,再分析资料(ERA、CFSR等)的大风风速往往比实况偏小(敖雪等,2018;范苏丹等,2017;孟宪贵等,2018;陈君芝等,2023)。渤海和黄海北部海岸线较长,尤其是渤海为我国内海,面积较小且被海岸环绕,沿海自动气象站较多。如何利用沿海、海岛等陆基站实况资料和数值预报产品,对海区的风场实况资料进行估算一直是科研和业务工作关心的重要课题。
以往的研究通过多种方法对海上大风风速进行订正,以海陆差异的定量分析及对模式产品的释用为主。赵强等(2008)、李燕等(2013)和曲巧娜等(2016)通过将一段时间内不同影响系统或不同风向下的沿海站资料分别与大中型客货轮站、浮标站、救助船站等资料进行对比,得出了渤海、黄海北部等部分海域与陆地大风差异的定量分析;赵金霞等(2014)对塘沽站和A平台站分别建立了极大风速和日最大风速之间的回归方程。另外,何群英等(2007)采用动力推算和热力订正的方法对MM5模式模拟结果进行订正;吴曼丽等(2013)应用卡尔曼滤波原理对中尺度数值预报产品进行释用,制作环渤海风的客观化定量预报产品;王亚男等(2019)使用递减平均法和渤海28个石油平台站、浮标站资料,对ROAD模式渤海区域10 m风速预报进行误差订正;杨晓君等(2019)采用欧洲中期天气预报中心(ECMWF)数值预报等模式产品,建立渤海BP神经网络海风预报模型;申华羽等(2020)利用浙江沿海观测站资料与ECMWF细网格10 m风预报进行不同风向下大风误差对比,进而推测海上大风;刘彬贤等(2018)基于A平台资料,运用集合最优百分位法对ECMWF集合预报的大风进行了订正;胡海川和周军(2019)基于集合平均、第75%分位值等统计量及不同量级风速发生的频率建立了渤海极大风预报客观订正方法。以上研究中,有的使用沿海站资料与浮标站、救助船站等资料对比分析了在不同影响系统或风向下海陆大风的差异性,但以定量分析为主;有些通过订正模式产品以获取海区风场信息,较少考虑影响系统及不同环流下数值预报的误差特征;有些研究采用的海基站点较少,没有充分利用海区周边的实况信息,因此应用范围有限。本文利用多年的浮标站、船舶站、石油平台站等海基观测资料,以连续、可靠的沿海和海岛等陆基站与数值预报产品等资料为基础,针对不同的大气环流类型,建立由沿海和海岛站风速实况推算海区风速实况的计算模型,从而实时获取黄渤海大范围、较为连续可靠的海区风场信息,作为海上监测的补充手段,更好地满足气象监测预警需求。
1 资料与检验指标
1.1 资料来源
使用的资料包括黄渤海沿海自动站、海岛站等陆基站以及海上浮标站、石油平台站、船舶站等海基站实况资料和ECMWF第五代全球再分析资料(以下简称ERA5)。使用2017—2021年逐时观测资料进行陆基站推算海区风速模型的建立和检验,其中,2017年1月至2020年12月的资料用于建立推算模型,2021年1—12月的资料进行检验。ERA5再分析资料用于天气分型和观测资料质量控制,选取2017年1月至2021年12月海平面气压场和10 m风场资料,空间范围为30°~42°N、117°~128°E,资料时间分辨率为1 h,空间分辨率为0.25°×0.25°。
1.2 站点资料特征分析
1.2.1 站点观测资料的时空分布特征
沿海自动站和大部分海岛站因维护较好,资料连续性好,较为可靠,将其作为“预报因子”推算海区风速;浮标站、石油平台站、船舶站等海基站位于不同海区,是海上大风监测数据的主要来源,将其作为“预报量”,针对此类站点所在海区建立推算模型。海基站具有较好的海区代表性,但由于建设和运行成本高、保障难度大,因此站点数量少,资料连续性较差。如为避免海冰导致设备毁坏,部分浮标站冬季将返回厂家维护而停止观测,而冬季正是大风最为频繁的季节;船舶站为北海救助局的救助船观测资料,在一定时期内锚定在固定位置,经常根据需要进行调整。
本文初选了黄渤海地区共109个自动站资料,考虑到陆基站的数量相对较多,剔除了缺测率达20%以上的站点,入选的陆基站(沿海站48个、海岛站26个)共74个;由于海基站点稀缺,仅剔除1个缺测率达90%的站点。其余的20个海基站中,17个站的位置稳定(图1a中绿色圆点);2个站的位置变动分别为0.16个经度和0.19个经度(图1a中蓝色方形),由于变动较小,忽略其影响;1个站的位置变动较大(图1a中红色三角形),将其作为2个站点处理,因此选取的海基站共计21个。最终共选取了95个自动站,具体位置如图1b所示。

图1 黄渤海地区自动站分布示意图Fig.1 Distribution of automatic stations around Yellow Sea and Bohai Sea Area
1.2.2 海基站观测资料的质量控制
由于海陆分布、站点地理环境较为复杂,海上站点密度较小,观测资料质量控制的难度较大。而海基站观测系统维护保障较差,异常的风速和风向常被作为判断故障的依据。本文将以下显著不合理的数据认定为疑误数据予以剔除:一是风速过大并超过一定阈值,或风速持续为零;二是风速不太小的情况下,风向却与环境风场差异较大,与环流形势不匹配。本文对ERA5 2020—2021年再分析资料检验表明,ERA5风向具有较高的可靠性,在不区分风力的情况下,与海基站相比,59%样本风向差在30°以内,78%的样本风向差小于60°;在6级及以上大风条件下,风向差在30°以内的占71%,60°以内的样本达85%,未有超过120°的站点。判断海基站风向异常的具体做法是将ERA5风场资料采用双线性方法插值到观测站点,当ERA5风力≥6级时,若观测风向与ERA5风向的夹角大于120°,则认为该观测资料是错误资料予以剔除。另外,本研究主要针对系统性大风进行推算,当有局地对流天气发生时,对流大风的风向可能与环境风场存在较大的差异,因此也可通过风向数据予以部分剔除。
1.3 检验指标
本文使用决定系数(R2)、均方根误差(RMSE)、偏差(Bias)等指标进行检验和对比,R2定义如下:
(1)
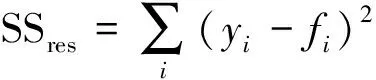
2 推算方法
2.1 环流分型方法
黄渤海海岸线复杂,受海陆分布和地形影响,不同海区风场差异较大,在不同的大气环流下呈现不同的特征,因此需要将天气形势进行分型,对不同类型的环流分别建立推算模型。采用ERA5的海平面气压场进行环流分型,时间为2017年1月1日至2020年12月31日,时间间隔为1 h,共35 064个样本。在计算天气形势分类之前对数据进行处理,为了部分消除中小尺度对天气形势分类的影响,降低了资料的空间分辨率,运用双线性插值方法将资料插值到0.5°×0.5°的规则格点上;另外,考虑不同季节海平面气压平均值存在一定差异,而风场主要与气压梯度有关,因此,将每个样本减去其空间平均值。天气形势分类的目的是找出气象要素场的若干分布模型类型,同一类的气象要素场分布特征相似,而不同类型的气象要素场分布有显著的差别(Huth et al,2008)。在欧洲国家科技领域合作研究(COST733)中,针对不同的天气形势分类方法开展了若干对比研究,结果表明,没有唯一最优的方法,其中k-means及相关方法得分较高(Huth,2010;Beck and Philipp,2010;Cahynová and Huth,2010)。k-means方法是一种非层级聚类算法,将一定数量的样本分为相互独立、互不包含的类别。使用k-means方法计算得到的距离,既可以用于分类,也可以用于计算类型归属。本文的计算方法和符号表达主要参考了文献Hoffmann and Schlünzen(2013)。
在k-means方法中,两个样本的相似性由欧拉距离平方SED来表示:
SED=‖x1-x2‖2
(2)
式中:x1和x2为两个气象要素场。样本簇内距离平方和记为WSS:
(3)
式中:x为簇Ci中的所有样本,zi为第i个簇的中心点(CC),k为簇的数量。
k-means方法在分类过程中,采用迭代方式,确定最小的WSS。首先是初始划分,选择k个中心点,计算每个样本和中心点的距离SED,所有的样本被指定属于离其最近的中心点;然后将属于同一簇的样本计算平均值,得到该簇新的中心点坐标;重复上述步骤,以新的中心点重新计算距离分配样本,并重新确定新的中心点坐标。如此迭代计算,直到各簇样本不再发生变化。

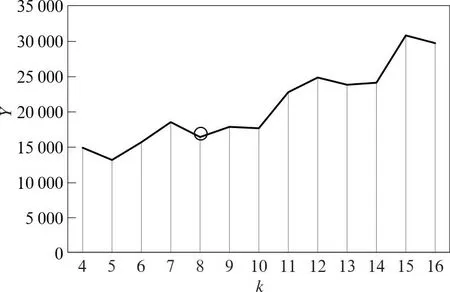
图2 Y-天气类型数曲线图Fig.2 Graph of Y-weather type number
8种天气类型的海平面气压距平分别呈现以下特征:Ⅰ型(图3a)为西南低东北高;Ⅱ型(图3b)为西高东低;Ⅲ型(图3c)和Ⅵ型(图3f)均为西北低东南高,Ⅲ型的气压梯度显著大于Ⅵ型;Ⅳ型(图3d)为均压场;Ⅴ型(图3e)和Ⅷ型(图3h)均为西北高东南低,Ⅷ型的气压梯度大于Ⅴ型,对应强冷空气;Ⅶ型(图3g)为西南高东北低。
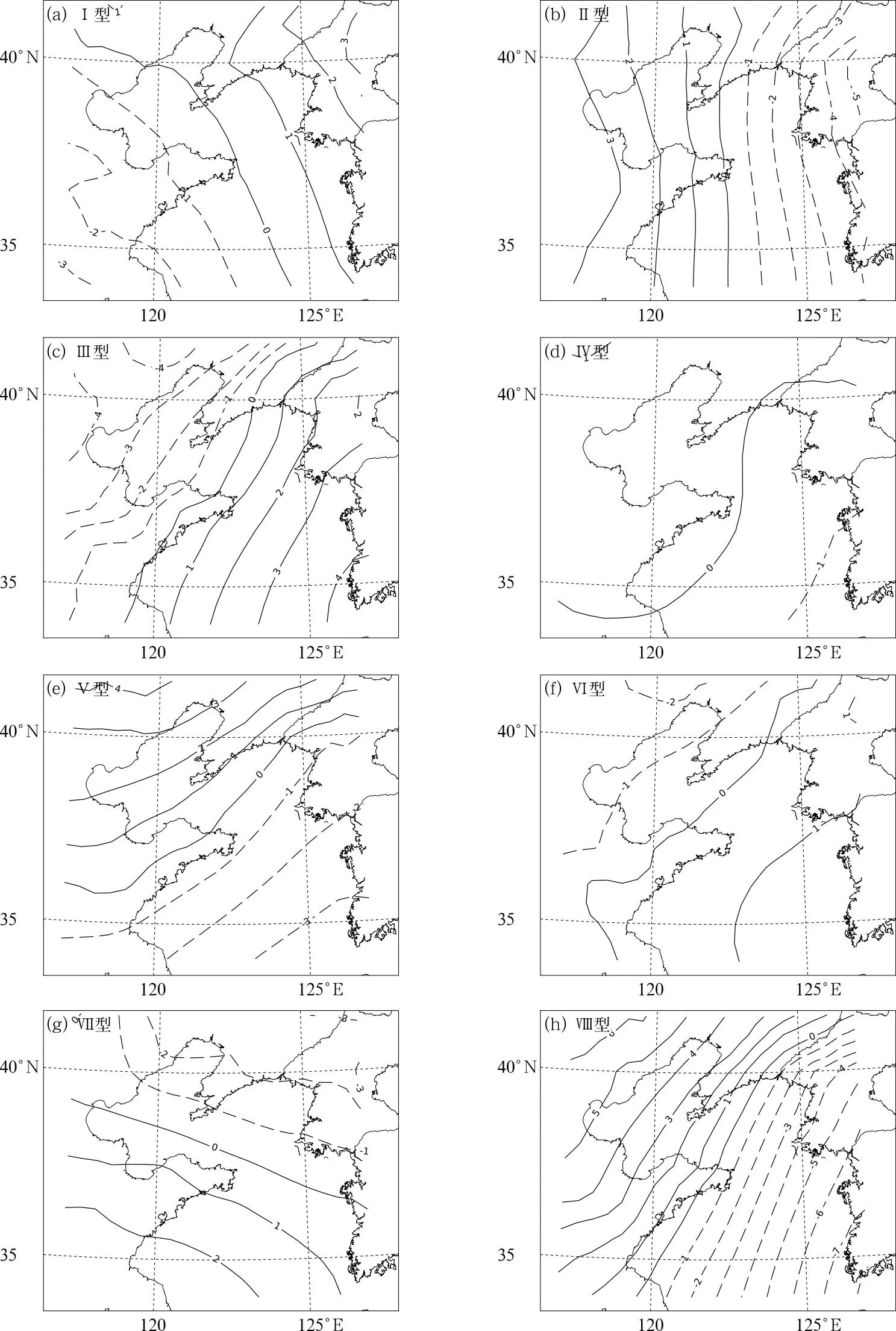
注:黑线为海平面气压距平(单位: hPa)。
8种天气类型中(全部样本),出现次数最多的天气类型是Ⅳ型,其次是Ⅵ型,占比最低的是Ⅱ型和Ⅷ型。以海基站中最大风力作为该时次的海上风力,统计得出不同风力下8种天气类型的占比(表1)。风力≥6、7级时,均为Ⅲ型占比最高,其次分别是Ⅵ型(≥6级,13.3%)和Ⅴ型(≥7级,15.9%),偏南大风的占比较高;风力≥8、9级则是Ⅴ型占比最高,其次是Ⅷ型,偏北大风尤其是偏东北大风占比最高。此外,分别统计8种天气类型下发生6级及以上大风的概率可知,Ⅷ型发生大风的概率最高,达94.7%,其次是Ⅲ型和Ⅱ型为70%以上,Ⅴ型和Ⅶ型为60%~70%,最少的是Ⅳ型(17.2%)。因此基于不同天气形势进行海区大风的推算是非常必要的。
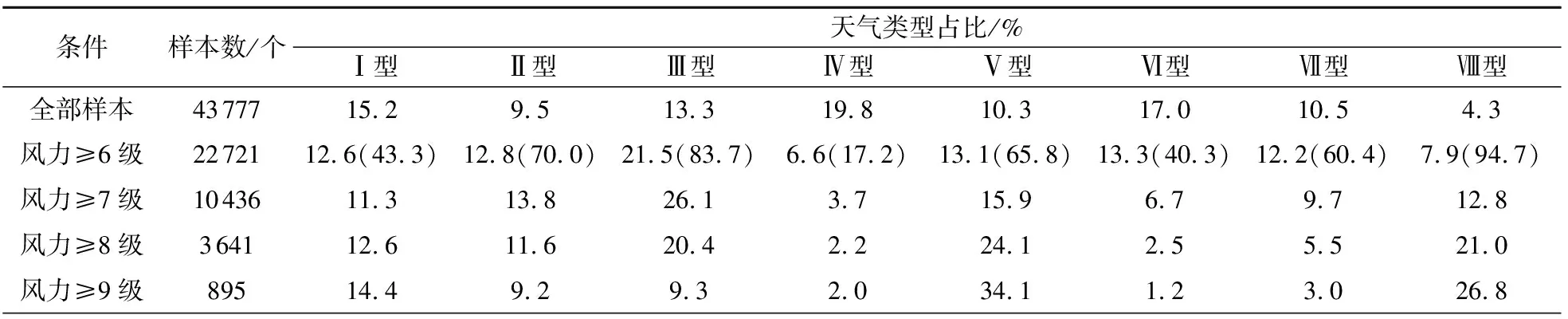
表1 2017—2021年不同风力等级对应的8种天气类型占比Table 1 Proportion of eight weather types at different wind force scales in 2017-2021
2.2 风速模型
使用2017—2020年的观测资料,针对海基站,逐站、逐环流类型建立沿岸风场向海区风场转化推算的模型,并使用2021年资料对推算模型的质量进行检验。本文尝试了多元线性回归、逐步回归等方法,经过试验对比,发现多元线性回归预报的误差最小,因此使用多元线性回归方法建立推算模型。由于在不同风速环境下,海基和陆基站风速的线性关系可能存在一定的差异,因此建立两种模型,并分别进行检验和分析:一是对全部风力等级建立模型(以下简称CM模型);二是针对海区大风的服务需求,将6级及以上的大风建立模型(以下简称HM模型)。推算模型的回归因子是74个陆基站风速,预报因子是21个海基站风速。线性拟合对资料样本长度有一定的要求,如果样本数太小,模型质量可能不高,但如果要求样本数过高,建模则会存在困难。本文设定了最低样本数,若某海基站、某天气形势下样本数小于该值,则放弃建立推算方程。最小样本数是通过批量试验来确定的,从100~800以10为间隔逐一进行建模和预报试验。其中,当最低样本数为400个时,HM模型的预报均方根误差最小;而对于CM模型,最小样本数为540个时,预报均方根误差为次小值,该样本数也较为合理。因此,将540个和400个分别作为CM和HM模型的最小样本值。CM模型共建立了161个方程,由于大风仅出现在部分环流形势下,发生次数和样本数量少,方程数量大幅减少,HM模型仅包含31个方程。以上方程均通过了F显著性检验(P<0.01)。需要说明的是,受样本数量的限制,本文建立的模型数量有限,尚不能覆盖全部21个海基站和8种天气类型。以CM模型2021年应用试验为例,全年获取的21个海基站逐1 h 观测资料数量为132 721个,缺测率约为27.9%,而风速推算的数据量为181 531个(推算率为98.7%),推算数据对实际观测数据有显著的补充作用。
3 结果分析
3.1 不同天气类型下的风速推算效果对比检验
利用2021年1—12月海基站逐1 h实况资料对推算风速进行了检验,采用散点分布、决定系数(R2)、均方根误差(RMSE)、偏差(Bias)等指标分别对8种天气类型下的风速推算结果进行分析。由CM和HM模型的检验指标对比分析(表2)可知,CM模型对全部样本推算的风速的R2为0.67,RMSE为2.05 m·s-1,Bias为0.01 m·s-1,整体比实况略偏小。对6级及以上大风推算,HM模型的RMSE和Bias分别为2.11 m·s-1和-0.34 m·s-1,均比CM模型推算的RMSE和Bias(分别为3.25 m·s-1和-2.03 m·s-1)偏小,可见,HM模型对大风天气的预报质量明显高于CM模型。
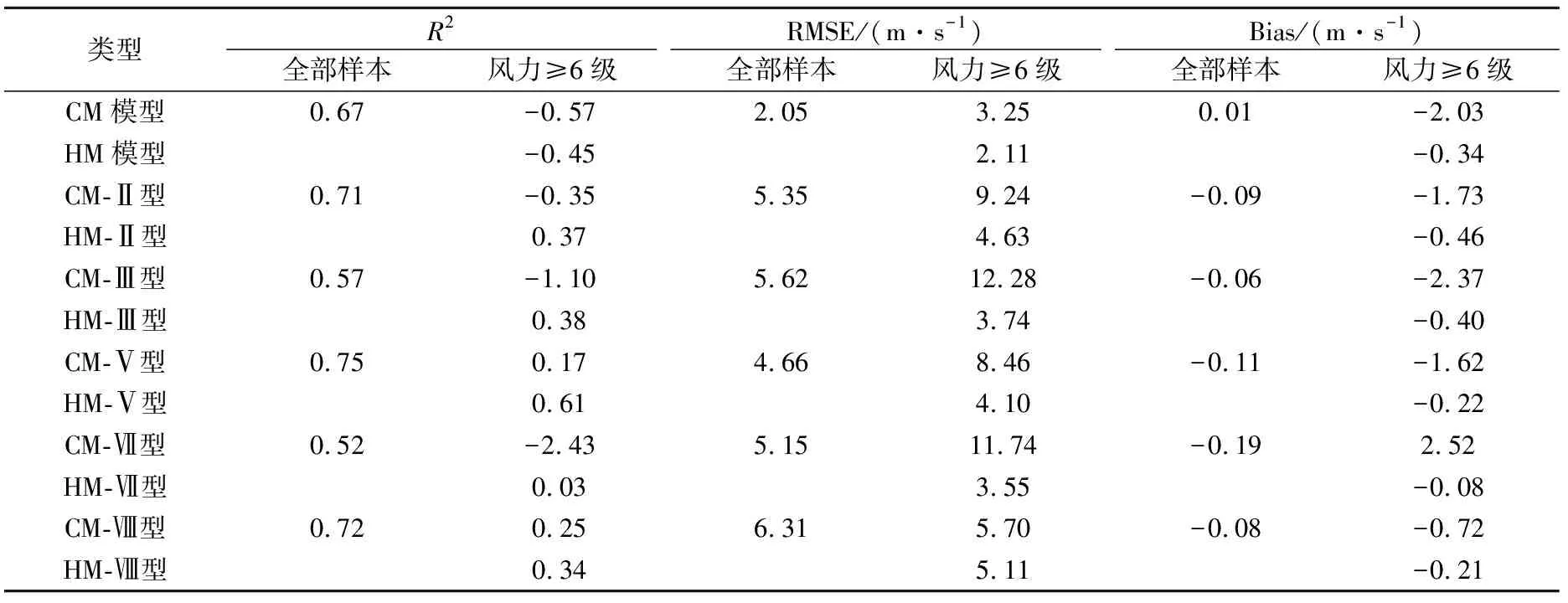
表2 CM、HM模型以及大风发生概率较高的5种天气类型风速推算结果检验指标Table 2 Test index of wind speed calculation results by CM and HM models and five weather types with high probability of strong wind
由推算结果与实况风速的散点分布(图4)可知,CM模式对4级以下风速推算,在对角线上方的散点略多于下方,即推算比实况偏大的站次略偏多;对4~6级风速的推算,对角线下方的散点略多于上方,即推算风速比实况偏小的站次略偏多;对于7级及以上风速的推算,推算风速比实况偏小的站次大于偏大站次。HM模型对于6~7级风速的推算偏大和偏小的数量较为接近,且集中在对角线附近,对于8级风速推算的偏小散点大于偏大散点,对于9~10级的风速推算与CM模型相似,以偏小为主。
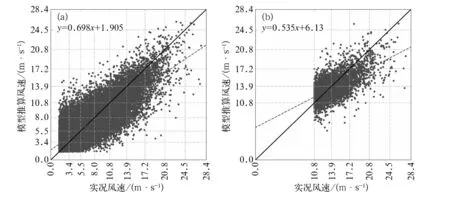
注:实线为对角线,虚线为拟合线。
将8种天气类型的CM模型推算结果进行对比(图5)可看出,Ⅴ型(图5e)和Ⅷ型(图5h)推算结果最接近对角线位置,效果最好;其次是Ⅱ型(图5b)对3~6级风速的推算接近对角线,效果非常好,对7~8级风速推算的偏小散点数量大于偏大散点,对9级风速的推算基本以偏小为主;Ⅰ型(图5a)、Ⅲ型(图5c)和Ⅶ型(图5g)的推算效果为:对3~5级风速的推算接近对角线位置,对6~7级风速推算的偏小散点数量大于偏大散点,对8级及以上风速的推算基本偏小;推算效果较差的是Ⅳ型(图5d)和Ⅵ型(弱)(图5f),此两种类型出现6级以上大风的概率较小(分别为17.2%和40.3%,表1),对6级以下风速的推算效果较好,对6级及以上的推算基本以偏小为主。由表2可知,以上天气类型中R2最大的为CM-Ⅴ型(0.75),其次是CM-Ⅷ型(0.72)和CM-Ⅱ型(0.71);RMSE最小的为CM-Ⅴ型(4.66 m·s-1)、CM-Ⅶ型(5.15 m·s-1)和CM-Ⅱ型(5.35 m·s-1)较小;Bias仅CM-Ⅶ型较大(-0.19 m·s-1),其他类型均小于0.11,且推算值均比实况偏小。

注:实线为对角线,虚线为拟合线。
通过以上分析可得出,CM-Ⅴ型和CM-Ⅷ型对全部样本的风速推算效果最好,其次是CM-Ⅱ型,CM-Ⅰ型、CM-Ⅲ型和CM-Ⅶ型相差不大,最差的是CM-Ⅳ型和CM-Ⅵ型。
对比5种发生6级及以上大风概率较高天气类型(大于60%)的HM模型推算结果可知,同样为对Ⅷ型(图6e)和Ⅴ型(图6c)的推算效果最好,推算的6~8级风速散点接近对角线位置,9~10级风速以偏小为主;对Ⅱ型(图6a)、Ⅶ型(图6d)和Ⅲ型(图6b)6~7级风速的推算效果相差不大,均接近对角线位置,Ⅱ型推算的8~9级风速以偏小为主,Ⅶ型的8级及以上大风较少且推算的风速偏小,Ⅲ型的8~10级大风在3种类型中最多且推算的风速基本偏小。

注:实线为对角线,虚线为拟合线。
表2给出了CM模型中对6级及以上大风推算的RMSE和Bias检验最小的是CM-Ⅷ型(5.70 m·s-1、-0.72 m·s-1),其次是CM-Ⅴ型(8.46 m·s-1、-1.62 m·s-1)、CM-Ⅱ型(9.24 m·s-1、-1.73 m·s-1),其他类型RMSE大于10.00 m·s-1,Bias大于2.00 m·s-1,推算的风速均比实况偏小。HM模型中推算的R2较大的是HM-Ⅴ型(0.61),RMSE较小的是HM-Ⅶ型(3.55 m·s-1)、HM-Ⅲ型(3.74 m·s-1)和HM-Ⅴ型(4.10 m·s-1),Bias较小的是HM-Ⅶ型(-0.08 m·s-1)、HM-Ⅷ型(-0.21 m·s-1)和HM-Ⅴ型(-0.22 m·s-1)。2个模型均存在风速估计偏小的问题,HM模型偏小的幅度显著小于CM模型。因此,对于海上大风使用6级及以上大风资料建立HM模型,可以得到更加准确的推算结果。
3.2 不同海区大风推算效果对比检验
为分析推算模型在不同海区大风过程中的应用效果,选取2021年海基站6级及以上大风观测数据,对推算结果进行检验。为保证统计的有效性,剔除缺测严重的站点,选取了样本数在41~1090的14个海基站点数据。从平均误差(图7a)和平均绝对误差(图7b)的分布可以看出,对渤海北部海区风速推算偏小,3个海基站的平均绝对误差为1.32、1.67、1.70 m·s-1;位于渤海西南部的5个海基站的推算中2个偏小、3个偏大,平均绝对误差分别为1.37、1.78、1.36、1.48、1.67 m·s-1;对渤海东部海区接近渤海海峡区域推算的风速偏小,2个海基站的平均绝对误差分别为1.54 m·s-1和1.61 m·s-1;对黄海北部海区的推算偏小,平均绝对误差为0.95 m·s-1;对黄海中部海区的推算偏小,3个海基站的平均绝对误差为1.41、1.58、1.67 m·s-1。由海基站的海区分布推算效果检验能够得出,对黄渤海大部分区域推算的风速偏小,仅对渤海西南部海区部分站点推算的风速偏大;推算的黄海北部海区风速平均绝对误差最小,对其他海区风速推算的平均绝对误差相差不大,在1.32~1.70 m·s-1。
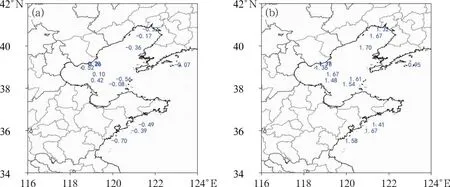
图7 海基站推算风速的(a)平均误差(单位:m·s-1)和(b)平均绝对误差(单位:m·s-1)Fig.7 (a) Average error (unit: m·s-1 ) and (b) mean absolute error (unit: m·s-1 ) of calculated wind speed at the sea-based station
3.3 大风过程推算结果个例分析
在以上研究中,采用数值预报产品中的海平面气压场判断环流的类型,运用已建立的方程根据实时的沿海和海岛自动站风速推算海区风速,由此建立海区风速的实时推算模型,以下将推算的海区风速与数值预报产品中的风向结合,绘制海区的实时风场分布图。通过对比2021年5次大风过程,对推算的效果进行评估。
原题呈现 (2018年荆门)如图1,等腰Rt△ABC中,斜边AB的长为2,O为AB的中点,P为AC边上的动点,OQ⊥OP交BC于点Q,M为PQ的中点,当点P从点A运动到点C时,点M所经过的路线长为( ).
图8是推算的6级及以上大风发生概率较高的5种类型海区风场与实况对比。2021年1月28日13时(北京时,下同)Ⅱ型(图8a)个例中,推算多个站平均风速为15.8 m·s-1,实况风速为16.2 m·s-1,平均绝对误差为1.6 m·s-1;2021年4月15日18时Ⅲ型(图8b)推算的多个站平均风速为14.6 m·s-1,实况风速为14.4 m·s-1,平均绝对误差为1.1 m·s-1; 2021年10月4日18时Ⅴ型(图8c)推算的多个站平均风速为15.2 m·s-1,实况风速为15.9 m·s-1,平均绝对误差为1.1 m·s-1;2021年5月7日04时Ⅶ型(图8d)个例中,推算的多个站平均风速为13.7 m·s-1,实况风速为12.8 m·s-1,平均绝对误差为1.6 m·s-1;2021年10月16日09时Ⅷ型(图8e)推算的多个站平均风速为15.7 m·s-1,实况风速为15.9 m·s-1,平均绝对误差为0.9 m·s-1。可以看出,5次过程中3次推算的风速比实况偏小,2次偏大,平均绝对误差较小,在0.9~1.6 m·s-1,推算风速与实况风速基本一致。从推算的海区风场中能够直观地看出渤海、黄海北部和中部的海上大风分布,为海洋气象服务提供支持。
海区风速推算方法,除推算结果较为准确外,还具有以下优势:一是适应能力强,易于业务应用,由于采用的是多元拟合方法建立方程,建模耗时非常小,当某陆基站资料出现缺测等异常情况时,可以剔除后重新快速建立计算方程并完成海区风速推算,不影响业务实时应用;二是可扩展性强,对于尚未建立预报方程的海区,随着资料的积累,可不断补充和完善,对于已经有足够资料积累的海区,可以考虑适当调整船舶、浮标等观测系统的部设,如移动到资料缺乏的海区,以更好地发挥作用。在有条件的情况下,也可对部分海区开展一段时期的试验观测以积累数据集。
4 结论与讨论
针对渤海和黄海海区海上大风观测资料稀缺问题,为有效补充海区风场实况获取能力,本文采用较为可靠的沿海和海岛等陆基站风速资料以及具有一定连续性的浮标站、船舶等海基站风场资料,建立了由陆基风场向海区风场的推算模型,并将推算结果进行检验,主要结论如下。
(1)在渤海和黄海北部被岸线环绕的海区,沿海气象站点较为密集的情况下,使用陆基站实况风速资料推算海区的风速是可行的。在海区观测不连续、不稳定的情况下,推算结果能够对海上风场资料进行有效的补充。以2021年21个海基站为例,使用CM模型可使海区数据获取率由72.1%提高到98.7%。
(2)根据海平面气压场对渤海、黄海北部区域的环流形势进行分类,并针对每一类环流,使用74个陆基站采用多元线性回归方法建立了21个海区站点的风速推算模型。检验表明,CM模型和HM模型均具有较高的可靠性,推算得到的风速均方根误差较小;在大风条件下,HM模型可得到更加准确的结果。
本文提出的海区大风推算方法具有较好的业务应用能力,但需要指出的是,本文对天气类型的划分主要针对天气尺度环流,推算模型对系统性大风天气具有很好的推算效果,但是对于局地对流性大风不具备推算能力。随着海上观测资料不断增加,观测模型可进一步细化和完善,准确率进一步提高;随着观测站点部设范围不断扩大,可以为更多海区建立推算模型,增强海上风场数据获取能力。
