基于改进Autogram的滚动轴承故障诊断

刘尚坤,张伟,孙宇浩,孔德刚,赵晓顺

(河北农业大学 机电工程学院,河北 保定 071001)

滚动轴承作为旋转机械中关键支撑部件,对保障设备的正常运行起着十分重要的作用,一旦其发生故障,将会造成生产事故甚至安全事故,因此对滚动轴承进行早期故障诊断意义重大[1].由于轴承的工作环境通常较为复杂,传感器拾取的轴承振动信号含有大量噪声及其他零部件的振动干扰成分[2],如何从非线性、非平稳、非高斯信号中提取出轴承早期故障特征并诊断其故障类型是重要的研究课题[3].

Moshrefzadeh等[4]提出了Autogram方法,该方法利用信号的无偏自相关峭度选择最佳解调频带识别故障,但峭度易受噪声及干扰成分的影响[5],导致所选最佳解调频带不准确、故障特征不明显、诊断可靠性低等问题.郑近德等[6]以改进的经验小波变换为基础,提出了一种能够自适应划分频带的自适应自相关谱峭度图方法.郑直等[7]将辛几何模态分解与Autogram方法结合,成功应用于液压泵故障的诊断.王慧滨等[8]利用变分模态分解(variational mode decomposition, VMD)对原始信号进行降噪处理,提出一种综合指标Z选出有效分量,再通过Autogram对所选取有效分量进一步处理,结合1.5维谱识别故障特征.王兴龙等[9]将最小熵解卷积(minimum entropy deconvolution, MED)与Autogram方法相结合,利用MED良好的降噪能力提高了选取解调频带的准确性.杨雨竹等[10]利用负熵构建了M指标,运用到经验模态分解(empirical mode decomposition, EMD)中筛选并重构本征模态函数(intrinsic mode functions, IMF)分量,再使用Autogram处理重构分量,提高了故障诊断准确率.上述关于Autogram的改进均利用到其他方法对信号进行前处理,再利用Autogram进行分析,虽提高了故障诊断效果,但增加了方法的复杂度和计算量.

胥永刚等[11]利用经验小波变换分解及重构信号对Autogram频带划分方式进行改进,有效提取了轴承故障特征,但是仍无法避免无偏自相关峭度指标受干扰影响较大的特点,容易产生解调频带选取不准确、故障特征频率不明显的问题.而平方包络负熵具有受噪声干扰小并能检测信号中周期性瞬变的特性[12],因此本文将平方包络负熵引入Autogram中,代替无偏自相关峭度指标,克服了峭度易受噪声及非周期异常脉冲影响的缺点,提出了一种利用平方包络负熵(spectral envelope negentropy,SEN)的改进Autogram方法,通过轴承内圈和外圈故障实验分析结果验证了所提方法的有效性.

1 理论基础

1.1 Autogram方法

Autogram方法是一种利用无偏自相关函数增强信号峰值、消除噪声干扰、筛选最优解调频带并通过平方包络谱识别故障频率的诊断方法,其步骤如下:

1)划分频带.最大重叠离散小波包变换(maximal overlap discrete wavelet packet transform,MODWPT)是基于小波变换理论的一种算法,能较好地处理非线性非平稳信号.利用其将时域信号按照二进树结构进行划分,分解系数可用wj,n,t表示,其中j为分解层数,共分解2j个不同频带,n为随分解层数j变化的索引,则分解系数可以表示为

(1)

2)计算频带的无偏自相关.无偏自相关可以去除信号中的无关成分,每个频带经无偏自相关计算后,信噪比得到提高,周期性成分得到增强.频带的无偏自相关计算如式(2)所示.

(2)

其中,x为经步骤1)划分频带的平方包络信号;τ=q/fs,为延迟因子且q=0,1,2,…,N-1;fs为采样频率.随着延迟因子τ的增加,用于计算无偏自相关的数据样本将减少,因此只保留部分无偏自相关值进一步计算.

3)计算频带峭度.峭度作为一种测量数据峰值的统计指标,可用于检测信号的故障冲击性,其定义可表示为

(3)

其中,x(ti)为时域信号,μx和N分别是数据集的平均值和长度.Autogram方法对步骤2)中频带的平方包络无偏自相关进行峭度值的计算,即

(4)

由式(4)计算得出各频带峭度值并构建信息图,选取峭度值最大的频带作为最优解调频带.

4)故障识别.计算步骤3)中最优解调频带的平方包络谱,分析其中的故障特征频率,对滚动轴承进行故障诊断.

1.2 平方包络负熵

轴承作为旋转机械中的关键部件,发生故障时会产生典型的周期重复瞬变信号,其特征是脉冲和循环平稳,检测重复瞬变的工具有谱峭度[13]、熵[14]和包络谱[15]等.Antoni[16]受热力学领域中熵的启发,将上述几种方法联系起来并进行了扩展,提出了平方包络负熵,用于衡量信号的冲击特征,其计算如下:

对于一个离散的时间序列X={x1,x2,…,xn},信息熵可表示为

(5)

其在频带[f-Δf/2;f+Δf/2]的复包络可表示为εx(n;f,Δf),序列xn(t)的平方包络表示为

εx(n;f,Δf)=|x(n;f,Δf)|2,

(6)

则平方包络负熵定义为

(7)

1.3 基于改进Autogram的滚动轴承故障诊断方法

为克服Autogram中峭度选取最优解调频带的不足,本文提出一种改进Autogram方法,利用了平方包络负熵受噪声干扰小且能够衡量信号中周期冲击成分的优点,以各频带的平方包络负熵代替峭度指标选择最优解调频带,再对最优解调频带进行平方包络谱分析,进而诊断轴承故障类型,流程见图1.

图1 改进Autogram方法故障诊断流程Fig.1 Fault diagnosis flow for improved Autogram method

2 实验研究

2.1 内圈故障实验

为了检验本文方法的有效性,对实验轴承故障信号进行分析,滚动轴承振动信号来自美国Case Western Reserve大学实验台[17],如图2所示.电动机转速为1 797 r/min,采样频率fs为12 kHz,实验轴承为驱动端轴承,型号为6205-2RS JEM SKF,表1为该轴承结构参数.内圈故障直径为0.177 8 mm,深度为0.279 4 mm,其振动信号的时域波形和包络谱如图3所示,包络谱中只有1倍故障频率谱峰较为突出,而由轴承局部损伤碰撞引发的多倍故障频率并不明显,不能准确判断轴承故障类型.

图2 滚动轴承实验台Fig.2 Rolling bearing test bench

a.时域波形;b.包络谱

表1 内圈故障轴承结构参数

采用Autogram方法对实验信号进行分析,Autogram信息如图4所示,选择的最优解调频带中心频率为4 593.75 Hz,带宽为187.5 Hz,最优频带的平方包络谱如图5所示,平方包络谱虽然有故障频率fi=162 Hz和转频fr=29.95 Hz,但是谱线成分较多不易区分,容易造成漏诊,且无法辨别其多倍故障频率,因此Autogram方法选择的解调频带滤波后的故障特征频率不够明显,无法准确进行故障诊断.

图4 内圈故障的AutogramFig.4 Autogram of inner ring fault

图5 Autogram最优频带的平方包络谱Fig.5 Square envelope spectrum of Autogram optimal frequency band

采用改进Autogram方法进行分析,各频带的SEN值如图6所示,中心频率为4 125 Hz,带宽为750 Hz的SEN值最大为0.9,将其选定为最优解调频带,该频带信号的平方包络谱如图7所示.与图5相比,经改进的Autogram方法处理的信号故障特征更明显,谱中能清晰地观察到故障频率fi的1～4倍频,且非故障频率成分被有效抑制,可以确定该轴承内圈出现故障.上述结果与Autogram方法相比,表明本文方法选取的解调频带更合理,SEN指标选取的最优频带有效地降低了干扰,所选频带更准确,其中蕴含的有效故障冲击成分更明显,诊断效果更好.

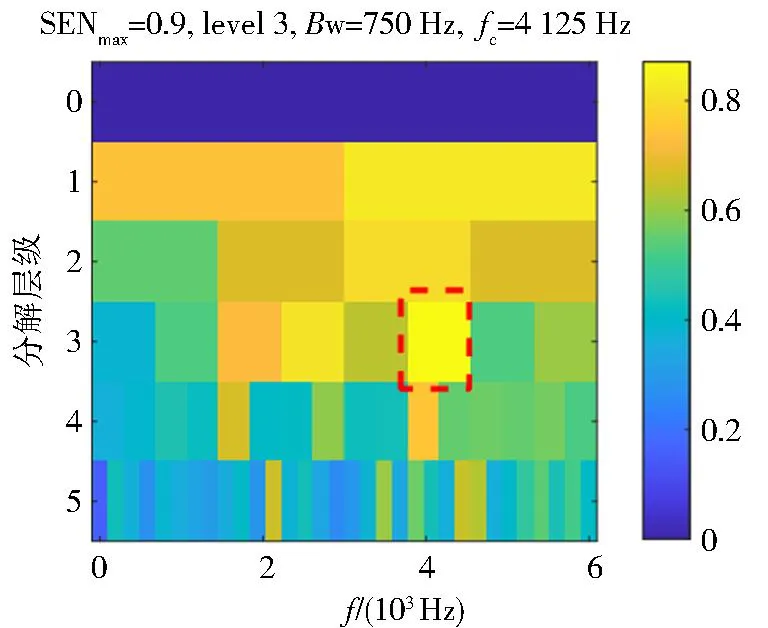
图6 内圈故障的改进AutogramFig.6 Improved Autogram of inner ring fault

图7 改进Autogram最优频带的平方包络谱Fig.7 Square envelope spectrum of improved Autogram optimal frequency band

采用快速谱峭度方法进行对比分析,图8为内圈故障的快速谱峭图.从图8可知,所选频带分解层级为0时谱峭度最大,其中心频率为3 000 Hz,带宽为6 000 Hz.因快速谱峭度方法选择原始轴承振动信号作为最优解调频带,其滤波后的平方包络谱与图3b相同,说明快速谱峭度方法无法准确诊断故障类别,较本文方法效果差.

图8 内圈故障的快速谱峭度Fig.8 Fast kurtogram of inner ring fault

2.2 外圈故障实验

外圈故障实验信号取自美国辛辛那提智能维护中心的滚动轴承全寿命实验[18],实验台结构如图9所示.传感器每隔10 min采样1次,采样频率为20 000 Hz,采样点数为10 000,滚动轴承型号为ZA-2115,其结构参数如表2所示,转速为2 000 r/min.实验结束后发现轴承1外圈发生损坏,其故障频率经计算为fo=230 Hz.

图9 外圈故障实验台结构Fig.9 Structure of outer ring fault test bench

表2 外圈故障轴承结构参数

选取第5 450 min时采集的数据进行分析,图10为此时信号的时域图及包络谱,图10中时域波形无法观察到明显的幅值脉冲,包络谱中虽有1倍故障频率成分出现,但其幅值不突出且无明显的倍频成分,不能准确地诊断轴承外圈发生故障.

a.信号时域波形;b.信号的包络谱

对采集的上述轴承信号,首先使用Autogram方法进行分析,图11为信号的Autogram图.由图11可知选取的最优频带分解层级为5,中心频率为7 343.75 Hz,带宽为312.5 Hz,该频带平方包络谱如图12所示,谱中仅能观察到故障频率fo的1倍频,并且干扰频率成分较多,难以准确判定轴承外圈故障,原因是峭度指标选取的解调频带不准确、不合理.

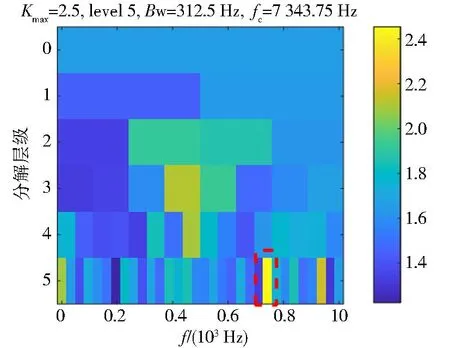
图11 外圈故障的AutogramFig.11 Autogram of outer ring fault

图12 Autogram最优频带的平方包络谱Fig.12 Square envelope spectrum of Autogram optimal frequency band

采用改进Autogram方法对此信号进行分析,计算各频带的平方包络负熵并构建信息图,如图13所示,选取的最优频带的SEN值为0.5,中心频率为3 750 Hz,带宽为2 500 Hz.图14为该频带的平方包络谱,谱中可以观察到故障频率fo的1～3倍频,且较清晰明显,通过此最优频带的平方包络谱可以准确诊断出该轴承外圈发生了故障.

图13 外圈故障的改进Autogram图Fig.13 Improved Autogram of outer ring fault

图14 改进Autogram最优频带的平方包络谱Fig.14 Square envelope spectrum of improved Autogram optimal frequency band

采用快速谱峭度方法进行对比分析,图15为该实验信号的快速谱峭图.由图15可知,选取的最优频带中心频率为7 500 Hz,带宽为1 666.6 Hz,该频带的平方包络谱如图16所示,谱中也仅能观察到外圈故障频率fo的1倍频,干扰频率成分多且复杂,难以准确判断轴承外圈故障,效果较改进Autogram差.

图15 外圈故障的快速谱峭Fig.15 Fast kurtogram diagram of outer ring fault

图16 快速谱峭度最优频带的平方包络谱Fig.16 Square envelope spectrum of fast kurtogram optimal frequency band

3 结论

针对滚动轴承早期故障诊断问题,提出了一种改进Autogram方法,将受噪声干扰小、能衡量信号周期冲击性的平方包络负熵指标引入到Autogram中,代替无偏自相关峭度指标,实验信号分析表明,该方法较Autogram方法、快速谱峭度方法选取的最优解调频带更合理,更能有效且准确地诊断出轴承内圈及外圈的故障,为滚动轴承的早期故障诊断提供了一条思路.