基于CNN集成和非均匀量化的家庭负荷预测*

徐 虎，刘新润，周 宣，薛 雷，苏永新

(1.威胜集团有限公司，湖南 长沙 410013；2. 湘潭大学 自动化与电子信息学院，湖南 湘潭 411105)

0 引言

家庭电力消耗占社会总能耗的30%以上，随着智能电网的发展和节能减排政策的推行，家庭负荷参与电力市场和需求响应备受关注[1].通过家庭负荷短期预测 ( HLSTF)获取未来几分钟到几小时的单个家庭的用电负荷，是家庭参与电力市场和需求响应的重要信息基础.准确的家庭负荷预测，能使用户更好地了解自己的能源使用情况，从而减少电能浪费，提高能源使用效率.同时，HLSTF对电力系统经济调度、电力系统安全维护和控制等方面具有重要价值[2].家庭负荷是电网供需平衡中需求侧的重要成分，家庭负荷短期预测能帮助电力系统提升电网应对风险的能力、降低电能生成成本及减少环境污染.

家庭负荷具有如下特性：1)受多种因素影响，具有多源不确定性.家庭电力消耗受气象、居民心理、节假日等因素的影响[3]，负荷的特征与规律复杂.单个家庭负荷缺乏空间上的统计和平滑作用，功率曲线不平滑、不平稳，不确定性强.2)大小功率分布不均衡，功率落差大.家庭中电灯、电视、传感器等中小功率电器运行时间长，而热水器、厨具、洗衣机、烘烤机等高功率设备运行时间短.

上述特点决定了HLSTF具有较高的难度，已有的预测方法主要是统计方法和人工智能方法[4].统计方法主要包括贝叶斯模型[5]、线性回归[6]、自回归综合移动平均[7]等.这类方法使用数学分析和统计工具来找出负荷的规律.面对复杂规律和多源不确定性，负荷规律的挖掘、表达、定参都面临着挑战，统计方法在HLSTF方面精度受限.

早期的人工智能方法包括前馈神经网络(FFNN)[8]、BP神经网络[9]及支持向量机回归 (SVR)[10]等方法，其预测精确性，显著优于统计方法.但由于经典神经网络的层数有限、支持向量回归强调用少量的参数表达数据规律，这些方法在抽取和描述复杂特征、规律方面存在原理性制约，制约了HLSTF精度.

近年来，深度学习飞速发展，主流网络包括递归神经网络(RNN)[11]和卷积神经网络(CNN)[12].HLSTF可视为时间序列预测问题，RNN类网络在HLSTF中最常用，RNN[11]、长短期记忆 ( LSTM)[13]网络、门控循环单元网络[14]等已广泛用于HLSTF.一些研究者注意到，家庭负荷受多种因素影响，但RNN侧重于时序间的规律，在提取多种因素的组合特征方面并不擅长，而CNN的最大优势在于特征提取，于是提出了CNN与RNN组合的方法[15].但这类方法普遍将CNN和RNN割裂开，将CNN某些层的输出作为RNN的输入[15]，特征缺乏指向性，导致预测结果可能受伪特征、无关特征的影响，从而影响预测精度.全连接网络具有很强的可塑性，能实现时序预测、特征融合等方面的功能，CNN与全连接网络能实现一体化学习，有望实现高质量的预测.如Binkowski等[16]用CNN与全连接网络组合对电力和金融进行预测，Koprinska等[17]应用CNN和全连接网络组合预测第二天的电力负荷和光伏太阳能，均取得优秀的预测成果.但家庭负荷影响因素众多，用单一CNN整体实现HLSTF，要求CNN具有较大规模，超参数的优化较为困难.集成学习利用不同的基础学习器处理不同难度、不同特性的问题，然后对其进行有机组合，形成强学习器，能获得优异的效果，尤其是其中的Boosting方法效果得到了普遍验证[18].家庭负荷的多源不确定性，可视为不同难度、不同特性的不确定问题的组合，与集成学习在模式上匹配，有望借助集成学习实现高精度预测.因此，本文将研究CNN与全连接网络构成多个学习器，通过Boosting集成，形成HLSTF模型.

CNN十分擅长处理图像，Imani[12]通过构建负荷图、负荷温度关系图，基于CNN实现家庭负荷关系的提取与表征，提升了HLSTF精度.但家庭与温度、湿度、风速等气象因素、是否节假日等有关，这些因素应与负荷组织成合适的形式，便于CNN从中提取规律与特征.

由于家庭负荷大小功率分布不均衡，且功率落差大.传统的负荷预测方案通常对家庭负荷进行均匀量化，造成中低功率段编码分辨率不足，高功率段占用的码元使用率不高，全局综合量化误差较大；高功率数据量少且其大小远离平均值，成为“异常”数据，这两方面均严重影响HLSTF精度.非均匀量化是解决这一问题的重要思路，Shepero等[19]将原始负荷数据转化为其自然对数后对家庭负荷进行概率预测，取得了较好的效果.但自然对数会将较低功率映射为极大的数值，不适用于机器学习.μ律非均匀量化能综合优化数据均匀性与数据范围，已被大量用于通信、信号处理领域[20].用μ律非均匀量化来改善HLSTF精度值得深入研究.

综上，为提高HLSTF精度，本文提出了一种基于CNN集成学习和非均匀量化的家庭负荷短期预测方法.本文贡献总结如下：第一，对家庭负荷数据进行μ律非均匀量化，缓解大小功率分布不平衡、功率落差大的问题；第二，将负荷数据、气象数据和节假日信息重塑为特征关系灰度图，便于CNN处理；第三，基于Boosting集成学习方法，集成多个CNN，适配家庭负荷的多源不确定性，实现高精度的HLSTF.该方法能为供电系统的用电管理部门和电力营销部门提供服务，制定更为灵活、动态的节能计划和营销策略，提高能源利用率，减少电力资源浪费.此外，还可以改善需求响应，并辅助家庭能源管理系统.

1 LSTF框架设计

本文以CNN集成学习为核心，设计HLSTF框架如图1所示.各模块的功能及其关联如下：

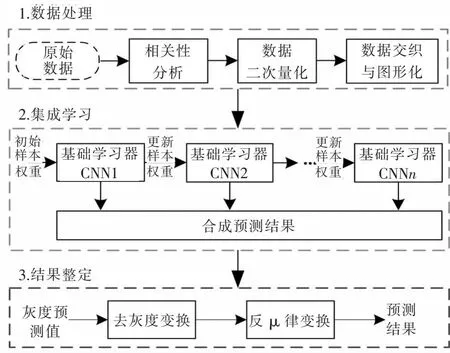
图1 家庭负荷短期预测框架Fig.1 Household load short-term forecasting framework

1)数据处理模块

该模块的核心功能是通过相关性分析找出对负荷影响较大的因素，之后对家庭负荷非均匀量化，并将HLSTF相关的数据转化为与CNN机制匹配的图像，为高精度预测提供信息基础.

现代家庭一般具有数字化仪表，通过对信号的均匀量化，得到各种原始数据.如“引言”所述，家庭负荷具有大小功率分布不均衡且功率落差大的特点，将严重影响HLSTF精度.因此要对原始数据进行二次量化，其目的在于根据原始数据的分布，对数据分布密集区，增加其分辨率，而数据分布稀疏区，降低其分辨率，并降低高低功率映射的数值落差，适配后续CNN学习的需要.

CNN处理图像的基本原理可视为，卷积核在待处理的张量上进行小步长、多步数的移动，每移动一次便计算卷积核与它所覆盖的张量之间的卷积值，通过监督学习机制，调整卷积核，实现指定的处理目标.不难看出，待处理图像自身的质量、规律，对CNN达成任务的质量、难度、计算量均有重要影响.家庭负荷与风速、温度、湿度、节假日等要素均有个体关系，同时又存在群体关系，因此，需要将功率数据与这些数据进行交织，然后再灰度图化，使CNN卷积核每次移动都能提取到与负荷相关的特征或规律，以提升预测精度、降低预测的计算量.

2)集成学习模块

该模块的核心功能是对二次量化后的负荷进行预测.其基本方案是基于Boosting的CNN集成学习.

该模块采用的基本原理是，首先基于CNN构建复杂程度低的基础学习器，各基础学习器通过Boosting方法协同，每个后置的基础学习器重点学习其前置学习器未能有效处理的样本，然后再将多个学习器的处理结果进行有机组合，形成预测结果.由于家庭负荷受多种不确定源及其耦合关系的影响，每种不确定源规律的提取、表达难度不同，这种集成学习的方式，本质上是前置学习器发现更简单的规律，而后置学习器和前置学习器一道发现更复杂的规律，用于HLSTF时，有望有效避免过拟合，为实现高精度预测提供学习模型基础.

3)预测结果整定模块

该模块的核心功能是将“集成学习”模块输出的灰度化等效负荷预测值，经过去灰度，反μ律变换转换为常规数据.

2 数据处理

2.1 负荷相关的因素分析

在影响家庭负荷的各类特征变量中，气象因素和节假日因素影响力最大[5].节假日信息可以被简单标记为工作日和非工作日，因此，无须进行分析和简化.然而，气象因素的种类较多，如温度、湿度、风速、露点和降雨量等.其中有的信息与负荷相关性强，而有的相关性弱.为了避免相关度较弱的信息对预测模型的影响，必须对其进行相关性分析，选出相关度较高的几类关键因素作为模型的输入变量.

本文采用互信息(Im)计算气象因素和家庭负荷之间的相关程度.Im的定义如下：

(1)

式中：I(X；Y)是气象因素X和家庭负荷Y之间的互信息值；p(x，y)是气象因素X和家庭负荷Y的联合概率密度函数；p(x)和p(y)分别是气象因素X和家庭负荷Y的边缘概率密度函数.

从UMASS数据集[21]中选取的实际家庭负荷数据和气象数据进行计算和分析，结果展示在表1中.

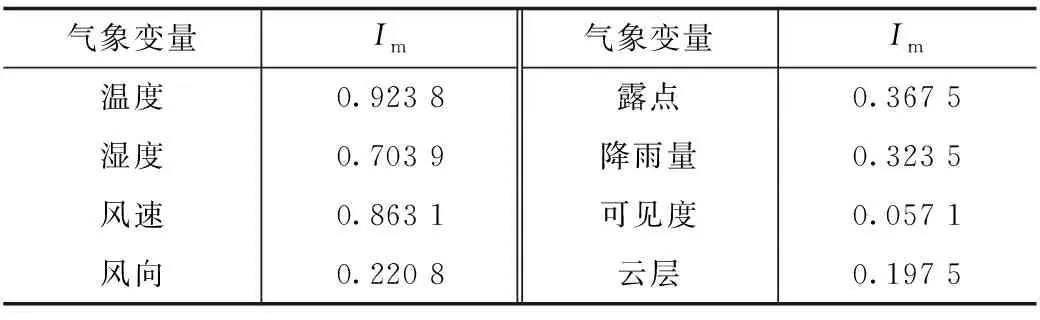
表1 家庭负荷与各类气象变量的Im

通过数据分析，除了前面选定的是否节假日信息和历史负荷信息外，本文另选取的气象变量为：温度、湿度和风速.此外，露点等变量相关性较弱，在本文中暂不考虑.

2.2 负荷数据的统计特性及分布重构

2.2.1 负荷数据的统计特性

从UMASS数据集[21]和REFIT数据集中收集到的204个家庭12个月的负荷数据，这些数据来自各个不同地区的单个家庭，对其进行统计分析，如图2所示.对功率Y出现的频次进行拟合，发现家庭负荷呈现近似于对数正态分布[22]，即：

图2 家庭小时级负荷概率分布Fig.2 Household hourly load probability distribution

lnY：N(μ，δ2)，

(2)

式中，N(μ，δ2)表示均值为μ、方差为δ2的正态分布.

通过观察家庭负荷分布发现，原始负荷的均值严重偏左，右侧有较长的拖尾.CNN等神经网络拟合数据的本质是挖掘出其统计规律，协调拟合的均值、方差.这样的偏态分布，将增加神经网络的学习难度.与此同时，这种偏态分布，将造成数据归一化时分辨率不合理、数据样本严重不均衡等问题.

2.2.2 基于非均匀量化的负荷数据分布重构

(3)

式中，μ为压缩系数.研究表明，μ取255综合量化误差较小且便于编码[20].

基于式(3)将原始负荷映射为正态分布的等效负荷，后续预测相关的处理中，用等效负荷取代原始负荷.

等效负荷、温度、湿度、风速数据均匀量化转化为256灰阶数据.其转换公式为：

(4)

式中：v代表待转换数据的原始值；vmin、vmax分别是待转换数据的最小值 、最大值；vcode是转换后的灰度值.

“是否节假日”信息也转化为灰阶表示，处于工作日，对应灰阶为0，处于节假日转为灰阶128.

2.3 数据交织与图形化

由于家庭负荷受历史负荷、温度、湿度、风速、节假日等影响，挖掘未来负荷与这些要素的关系是HLSTF的本质任务.考虑到数据的时间序列特性，预测系统设计为基于时段[t-23，t]的各要素数据，预测t+1时段的家庭负荷，其中，t代表时段t，时间步长为1 h.为保证后续CNN学习中，卷积核每一步移动都能包含负荷信息，都能抽取到负荷与它的影响要素之间的关系，将负荷和它的影响要素交织，形成图3，其中负荷已用等效负荷置换.

图3 负荷及其影响因素交织图Fig.3 Interlace diagram of load and influencing factors

图3为7×24的二维平面.显然，当卷积核的横向覆盖不低于2、竖直覆盖范围不低于2时，CNN的第一个卷积层就能方便地提取如下关系：1)负荷自身时序关系；2)负荷分别与温度、湿度、风速、节假日的关系.后续卷积层的卷积核只要规模大于2×2，都能有效提取负荷与温度、湿度、风速、节假日的关系，这种数据组织方式能为CNN学习带来高效性和灵活性.

3 负荷预测

3.1 CNN基础学习器

设计基础学习器CNN的结构如图4所示.基础学习器输入图3所示的数据时，给出第25时段的家庭等效负荷预测值.

输入层负责接收数据，本文中CNN模型的输入是尺寸为7×24包含5种特征的24 h相关值的二维灰度图.

本文为了避免提取到的重要特征被丢弃，在设计的结构中没有使用池化层.在设计卷积核尺寸大小时，考虑到应用更多的卷积核能得到更多的特征映射，但随着卷积核数量的增加，CNN的可学习参数也随之增加，可能会导致过拟合问题.最终通过实验优选，CNN层的参数设置为：

第1个卷积层：卷积核大小为2×5，卷积步长为1×3，通道数为32；该层用于提取负荷及其影响因素之间的显性特征，采用32个通道共提取出32种特征.

第2个卷积层：卷积核大小为2×5，卷积步长为1×3，通道数为64；该层用于提取负荷及其影响因素之间的隐性特征，采用64个通道共提取出64种特征.

其中，两个CNN层共同的设置为：为了防止边缘信息计算程度不够，提取不充分，padding设置“same”边缘填充像素.激活层用于提供非线性，以便从输入数据学习非线性关系，激活函数选用ReLU.

输入数据通过两层CNN的特征提取后，将数据展平为一维数据，由于数据尺寸较大，先经过一层神经元个数为128的全连接层，激活层采用ReLU.此外，为了防止模型的过拟合，使用了系数为0.3的dropout层.最后经过一层神经元个数为1的全连接层用于输出提前一步的等效负荷预测值.

对于单个CNN的训练，根据标准的梯度反向传播算法来实现CNN参数的更新.其损失函数定义如下：

(5)

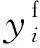
3.2 集成策略

考虑到家庭负荷关联因素多，不确定性强，规律复杂，采用Boosting算法中的Adaboost集成学习方法，来协调多个CNN，提高预测的准确性和鲁棒性.在本文实验中，基础学习器设置为3个，基础学习器的训练轮数设置为100轮，学习率取0.000 1.该集成策略的核心有2个：①根据各个样本在各基础学习器处理后得到的相对误差来调整各样本的权值，相对误差越大的样本，后续权值越高；②根据各个基础学习器对各样本的误差，定量调节其在最后结果中的重要程度.

4 预测结果整定

基于训练好的强学习器，得到等效负荷预测结果，应对其进行去灰度，反μ律变换，得到常规负荷预测数据：

(6)

(7)

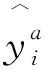
5 测试与分析

5.1 数据集、度量与设置

来自多个不同地区的不同用电模式的家庭负荷数据集用于验证本文所提方法的有效性和可靠性[21]，下面将详细展示与分析其中两个有着明显差异的家庭的预测结果，分别记为家庭A和家庭B.其中，家庭A位于美国东部，属于亚热带湿润气候[21].家庭B位于英国，属于温带海洋性气候.利用家庭A[21]、家庭B的公开数据集进行相关实验.将一整年的家庭负荷数据集进行重复交叉试验，共计8 760个小时家庭负荷数据，20次重复试验.将家庭A 2014年6月1日至6月8日的负荷数据用作测试集展示预测结果，家庭B 2014年12月1日至12月8日的负荷数据用作测试集展示预测结果.

实验中，为了利用多个时间步长的时间序列信息，使用了滑动窗口方法.选择前24 h的历史数据作为输入，预测后1 h的负荷数据.以1 h为步长，依次完成家庭负荷预测.

本研究选取平均绝对百分比误差(MAPE)、均方误差(MSE)、均方根误差(RMSE)、平均绝对误差(MAE)作为评价指标.

5.2 实验算例设计

为了验证本文所提模型的有效性，针对A、B家庭均设计了以下几个实验算例.为了进行公平比较，所有算例都采用相同的训练集和测试集.

算例1：采用本文所提方案，即包括本文第1节到第3节所设计的内容.以下称为“本文方案”.

算例2：学习模型及其参数设置与本文方案相同，但输入数据不通过二次量化和数据交织与图形化处理，而是最大-最小归一化后按时序输入模型.以下称为“无二次量化与数据交织”方案.

算例3：学习模型及其参数设置与本文方案相同，但负荷数据不采用本文所提的二次量化方法，而对原始负荷归一化处理后，再进行数据交织与图形化处理.以下称为“无二次量化”方案.

算例4：CNN结构及其超参数设置与本文方案相同，但采用单个CNN进行预测，不使用集成策略.以下称为“无集成策略”方案.

算例5：采用SVR模型预测[10].核函数选用径向基，核系数和惩罚参数设置与文献[10]一致.

算例6：采用FFNN[8]预测.FFNN结构采用文献[8]方案，采用4层神经网络，每层神经元个数分别为8、1 500、800和1，输入为每日时间、每周时间、每月时间、假日信息和温度，激活函数为sigmoid，使用“Adam”优化器，学习率为0.000 5，训练轮数为200.

算例7：采用LSTM模型预测[13].本算例LSTM网络结构为3层，神经元个数都为25，后面接两层全连接网络，神经元个数分别为25和1，使用“Adam”优化器，学习率为0.000 5，训练轮数为400.

测试中，硬件环境为：1080Ti 双显卡、32GB 内存、i7-8700CPU的计算机，软件环境为：Tensorflow1.14.0、Keras2.3.1.

5.3 实验结果分析

家庭A和家庭B分别使用算例1与算例2～算例7的预测误差及精度对比如表2和表3所示.

表2 家庭A不同算例的预测误差及精度对比

表3 家庭B不同算例的预测误差及精度对比

从表2和表3中可以看出：

1)本文方案的预测误差最小，家庭A的MAPE、MSE、RMSE和MAE分别低至0.326 3、0.414 5、0.643 8和0.343 9，家庭B的对应指标分别低至0.2654、0.0343、0.1853、0.1289.与算例2～算例7所给出的6个算例相比，家庭A的MAPE降低了6.8%～57.8%、MSE降低了21.8%～41.1%、RMSE降低了11.5%～23.3%、MAE降低了14.6%～39.2%，家庭B的对应指标分别降低了4.0%～50.0%、14.5%～72.5%、7.5%～47.5%、8.0%～47.9%，说明本文提出的二次量化方法、数据交织与图形化方法、CNN、集成学习算法等综合作用时，预测精度优于LSTM、SVR、FFNN、单个CNN等方法.此外，在20次重复实验的情况下，本文方法仍获得了最优预测结果，证明了本文方法的稳定性和可靠性.

2)在算例2～算例7中，无二次量化方案和无集成策略方案的预测误差较其他算例小.无二次量化方案和无集成策略方案均采用了本文涉及的CNN，两者误差较小，说明本文CNN设计的合理性，其预测效果已能超过LSTM.

3)无二次量化与数据交织方案、SVR和FFNN的预测误差较大.无二次量化与数据交织方案误差大，而无二次量化方案、无集成策略方案误差小，综合说明设计的方法不适合数据不图形化的方案，究其原因是，不能充分发挥CNN在图像处理方面的优势.

家庭A和家庭B使用本文方案的算例1预测曲线分别如图5和图6所示，家庭A和家庭B使用算例2～算例7的预测曲线分别如图7和图8所示.对比图5、图6、图7和图8可以看出，本文方案的预测结果能最紧密地跟随实际数据的变化趋势.

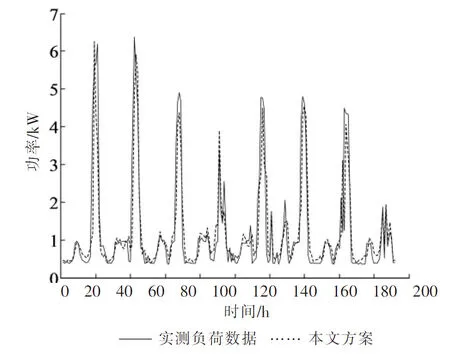
图5 家庭A中算例1的预测曲线Fig.5 The prediction curve of example 1 in home A

图6 家庭B中算例1的预测曲线Fig.6 The prediction curve of example 1 in home B

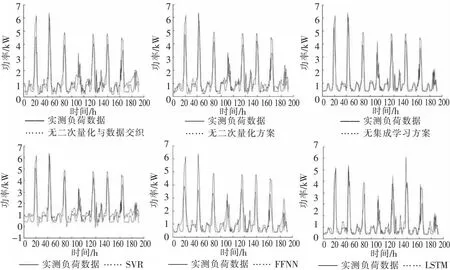
图7 家庭A中算例2～算例7的预测曲线Fig.7 The prediction curve of example 2-example 7 in home A

图8 家庭B中算例2～算例7的预测曲线Fig.8 the prediction curve of example 2～example 7 in home B

将本文方案与无二次量化方案进行比较，从图7、图8中可以看出，无二次量化方案在低功率区域的预测结果存在明显的偏差，在高功率区域也无法进行准确的跟踪.这是因为家庭负荷分布不均衡，功率落差大，而无二次量化方案缺少二次量化过程对负荷数据的调节，导致中小功率部分分辨率不足、高功率部分分辨率冗余，从而使模型学习不足，小功率和高功率预测准确率较低，预测精度受限.

将无二次量化与数据交织方案和无二次量化方案进行对比，从图7、图8中可以看出，无二次量化与数据交织方案在小功率区域的预测结果更差，高功率区域同样无法进行准确的跟踪，这是因为无二次量化方案比无二次量化与数据交织方案多了数据交织与图形化过程.从表2和表3中得出，“无二次量化”方案与“无二次量化+数据交织”方案相比，家庭A预测结果的MAPE、MSE、RMSE和MAE分别降低了14.1%、16.8%、8.8%，11.2%，家庭B的对应指标分别下降了28.7%、29.0%、15.7%和22.2%，证明了将HLSTF预测问题转化为图像处理问题是有效的，通过数据交织与图形化可以充分利用CNN在图像处理方面的突出优势.同时，这种二维灰度图包含负荷及其影响因素之间丰富的非线性关系，为高精度预测提供信息基础.此外，将本文方案与无二次量化与数据交织方案进行对比，再次验证了本文所提出的数据处理过程的必要性，非均匀量化能很好地处理家庭负荷分布不均衡的问题，将输入数据进行数据交织与图形化便于CNN高效处理，同时更加充分地挖掘输入特征之间的非线性关系.

将本文方案与无集成策略方案进行比较，从图7、图8中可以看出，无集成策略方案在小功率区域跟踪得比较好，在高功率区域有跟不上或者超出真实值的情况，这是因为无集成策略方案没有采用集成策略，只使用单一的CNN模型进行预测，由于家庭负荷受多种不确定源影响表现出复杂特性，单个模型难以学习到所有特性，导致模型在小功率和大功率之间难以取得平衡，往往只能兼顾一个方面.而本文方案采用集成策略，以CNN为基础学习器，多个学习器协同工作，将学习到不同特性的CNN集成起来形成强学习器，能有效实现高精度预测.本文方案具体使用3个CNN模型进行集成，第2个CNN可以对第1个CNN学习不到的区域进行加权再学习，第3个CNN又可以对第2个CNN学习较差的区域进行加权再学习，通过3个CNN的接连学习后，最终得到的集成预测器即可对家庭负荷进行准确预测.

将本文方案与SVR、FFNN和LSTM进行比较，SVR在小功率区域预测结果最差，导致MAPE值最大.这是因为，虽然SVR擅长用少量的参数表达数据规律，避免过拟合问题，但是，面对特征复杂的家庭负荷领域，该特点使其在表达复杂特性方面差于神经网络模型.FFNN在小功率区域的预测结果较好于SVR，但是在高功率区域跟不上实际负荷趋势.这是因为FFNN可调参数多于SVR，在表达非线性关系上优于SVR.但FFNN在功能上不如深度神经网络具有针对性，面对复杂的输入数据既不能提取时间特性，也不能提取组合特性，致使模型难以学习复杂输入数据的规律，在面对分布不均衡的家庭负荷时，预测结果差于LSTM.相较于SVR和FFNN，LSTM的预测结果最好，特别是在小功率区域能较为准确地跟踪真实负荷趋势.这是因为LSTM具有记忆功能，能够处理时间序列中隐含的长期依赖关系，应用在具有时序特征的负荷预测中有着明显的优势.但预测结果还是差于本文方案和无集成策略方案.将LSTM与无集成策略方案进行对比，从表2和表3中得出，无集成策略方案相比“LSTM”方法，家庭A预测结果的MAPE、MSE、RMSE和MAE分别降低了9.8%、6.8%、3.4%和3.7%，家庭B对应指标分别下降了5.5%、53.6%、31.9%和15.4%，验证了LSTM在提取负荷及其影响因素的组合特征方面不如CNN，难以挖掘其中隐含的非线性关系，而CNN利用其在图像处理上的优势，将负荷及其影响因素转化为具有数据交织的二维灰度图，使模型能获得更高的预测精度.此外，SVR、FFNN和LSTM都是对家庭负荷进行均匀量化，由于短期家庭负荷服从对数正态分布，致使模型的输入是偏心的分布，这增大了机器学习的难度，制约学习模型的预测性能.

将无集成策略方案与SVR、FFNN和LSTM进行比较，从图7和图8中可以看出，无论是小功率区域还是大功率区域，无集成策略方案的预测结果均优于SVR、FFNN和LSTM.验证了将输入数据重塑为特征关系灰度图，搭配CNN强大的特征提取能力作为预测模型的方案是可行的，所提出模型的预测性能优于SVR、FFNN和LSTM模型，说明了CNN在时序预测问题上的巨大潜力.

6 结语

电力系统的稳定运行和经济调度都离不开电力负荷预测，高精度的家庭负荷短期预测不仅为公共部门制定灵活的电价制度提供便利，还为用户自身参与需求响应提供重要信息基础.为实现高精度HLSTF，提出了一种基于CNN集成与非均匀量化的家庭负荷短期预测模型.首先，将HLSTF负荷数据进行μ律非均匀量化，再将负荷与它的影响因素进行交织，构成灰度图.然后，以CNN为基础学习器，基于Adaboost集成学习实现提前一步的等效负荷预测.继而，将预测的负荷等效表达转换为常规表达.最后，基于某家庭一年实测数据，进行实测与分析.有以下结论：

1)负荷非均匀量化处理能有效解决家庭大小功率分布不均衡的问题，提高模型预测精度.

2)将与负荷具有内在联系的数据进行交织，转换为二维灰度图，能充分发挥CNN的图像处理优势，获得高精度预测.

3)CNN可以学习不同尺度上数据点之间的非线性关系，集成策略能解决单一模型无法兼顾低功率和高功率预测的问题，提高模型的准确性和鲁棒性.

本文提出的家庭负荷超短期精准预测方法可用于家庭能源管理、家庭参与电力市场交易、为能源管理和优化提供预测信息等场合，助力电力系统安全稳定经济运行以及家庭和社会节能减排.

本文方法能应对预测对象的多源不确定性和幅值分布不均衡，可推广应用到车流量预测、网络流量预测、风速预测等场合.下一步将探索将本文中的CNN改成循环神经网络，进一步拓展其应用领域.