基于逐步多元线性回归和随机森林模型预测黄河流域极端气温事件
2024-03-14陈俊清杨雪宁刘峰贵
陈俊清,李 毅,王 斌,杨雪宁,刘峰贵
(1. 西北农林科技大学 水利与建筑工程学院,教育部旱区农业水土工程重点实验室,陕西 杨凌 712100;2. 水利部黄河流域水治理与水安全重点实验室(筹),河南 郑州 450003; 3. 澳大利亚新南威尔士州初级产业部,澳大利亚 新南威尔士州 NSW 2650; 4. 青海师范大学 地理科学学院,青海 西宁 810016)
0 引言
联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change, IPCC)第六次报告指出,2001—2020年全球平均地表温度较1850—1900年升高约0.99 ℃[1]。全球变暖背景下,干旱、暴雨和热浪等极端事件呈增加态势,不仅加剧了旱涝灾害、造成农作物减产,而且严重危害了人体健康[2]。极端气候事件是指天气变量观测值超过某一阈值时的小概率事件[3]。气候变化检测和指数专家组(Expert Team on Climate Change Detection and Indices, ETCCDI)定义了27个具有代表性的极端气候指数[4],包括极端气温和极端降水两大类指数,已被广泛应用于全球或区域尺度极端气候研究[5]。其中ETCCDI定义了16个极端气温指数(extreme temperature index, ETI),可从不同角度评估极端气温事件,例如强度指数有最高气温(TXx)和最低气温(TNn),相对阈值指数有暖昼天数(TX90p)和冷夜天数(TN10p),以及绝对阈值指数霜冻天数(FD0)等[6-7],而酷热天数(TD30)作为表征极端气温事件的绝对阈值暖指数,在极端气温事件评估中具有很好的适用性[8]。
大量研究人员对极端气温指数进行分析预测,为缓解气候变化可能造成的不利影响提供了参考。研究者们采用多种方法对ETI与其关键影响因子进行建模,并预报极端气温事件。如逐步多元线性回归模型(stepwise multiple linear regression, SMLR)可较好地描述极端气温指数与多个影响因子之间的定量关系,如CHEN等[9]利用SMLR模型量化分析了湖北省植被对极端气候指数的敏感性。随着大数据时代的到来,各种机器学习模型被广泛应用,其中随机森林(random forest, RF)模型是BREIMAN[10]建立的一种组合式机器学习方法,具有准确性高、不易过拟合的优点,能有效处理大数据集并判定变量的重要性。LI等[11]利用机器学习方法对北京地区网格温度进行了预报。ZHOU等[12]对比了多元线性回归(multiple linear regression, MLR)、梯度提升决策树、k-最近邻法、随机森林、极端梯度提升(extreme gradient boosting, XGB)和深度神经网络(deep neural network, DNN)等6种机器学习方法对近地面气温的预报。
此外,极端气温事件与大气环流变化的密切联系为极端气温事件的预报提供了新的研究方向。大气环流会促进高低纬度之间及海陆之间的水热交换,是影响气候的重要因素。大气环流异常往往会导致极端气温事件的发生,因此,常用环流指数来定量表征大气环流的变化,而大气环流通常分为大气类、海温类和其他三类。目前,已有诸多学者开展了大量针对极端气温事件影响因素的研究,发现大气环流对极端气候事件的发生具有重要影响[13-14]。梁苏洁等[15]分析并采用了北极涛动、北大西洋涛动、太平洋—北美型和平流层极涡4种大气遥相关型指数构建了多元回归统计方程对华北地区冬季极端低温事件进行了预测。戴声佩等[13]对华南地区极端气温事件进行大尺度环流影响分析,指出厄尔尼诺—南方涛动(El Nio-Southern Oscillation, ENSO)异常与华南地区极端气温事件关系密切,南海副高强度指数和西太平洋副高强度指数也对极端气温事件有明显贡献。
黄河发源于青藏高原,是我国第二大河,流经内蒙古高原、黄土高原和黄淮海平原,最终汇入太平洋。黄河流域位于32°N~42°N,96°E~119°E,面积约7.95×105km2,主要是干旱半干旱地区,其年平均降水量为123~1021 mm,年平均气温为-4~14 ℃[16]。全球变暖背景下,黄河流域极端气温事件频发,苗书玲等[17]发现黄河流域极端气温指数在流域西北部有明显的下降趋势,东部则上升趋势明显。张克新等[18]也发现黄河流域极端气温事件和厄尔尼诺—南方涛动(ENSO)指数存在多尺度的显著相关性。尽管目前国内对极端气温事件的时空变化及其成因分析已有相关研究,但研究大多采用主成分分析[19]、基于SPSS软件的因子分析[13]等统计分析方法,对于RF等机器学习模型的应用还较少。此外,诸多学者在单个大气环流因子如ENSO对极端气温事件的影响方面取得了成果[20],但极端气温事件的成因复杂,受到诸多因素的共同作用,综合考虑多种大气环流因子对黄河流域极端气温事件的预测研究还不够深入。黄河流域是气候变化的敏感区,长期以来,频发的极端气温事件对该区域生态系统和人类生活造成严重影响。探究黄河流域极端气温事件的气候驱动要素及其预测,能够为适应气候变化、流域生态环境保护和防震减灾提供重要的科学依据。
本文在收集1961年1月—2022年10月环流指数数据和1961年1月1日—2020年12月31日黄河流域80个站点气温数据的基础上,分析黄河流域极端气温事件的时空分布特征及其对环流的响应规律,运用SMLR和RF模型模拟极端气温指数,并利用环流指数对未来极端气温指数进行预测,以期揭示黄河流域极端气候事件的变化规律及成因,为极端气温的预报提供科学依据。
1 材料和方法
1.1 数据收集
黄河流域80个气象站点1961年1月1日—2020年12月31日的逐日气温数据来源于中国气象科学数据中心(http://data.cma.cn),经检查该数据具有一致性和完整性,数据缺失率<1%,如图1所示。
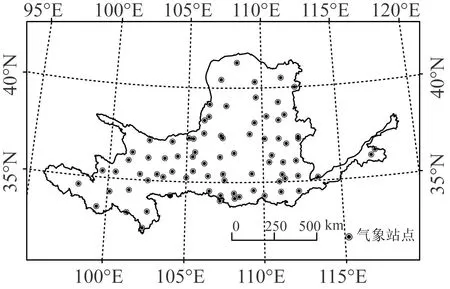
图1 黄河流域气象站点空间分布Fig.1 Spatial distribution of weather stations in the Yellow River Basin
研究选取1961年1月—2022年10月130个环流指数的逐月数据,该数据来源于国家气候中心(http://cmdp.ncc-cma.net/cn/download.htm),为保证数据的连续性,将连续缺失3个月及以上的环流指数剔除后保留了100个环流指数。
1.2 极端气温事件关键驱动环流指数筛选
1.2.1 极端气温指数的选取和计算
选用描述频率和强度的6个极端气温指数,其中5个是ETCCDI定义的(http://etccdi.pacificclimate.org/list_27_indices.shtml),包括TXx、TX90p、TNn、TN10p和FD0。另一个选用的极端气温指数TD30具有生物学重要性且被广泛应用于极端气温事件研究[8]。TXx、TX90p和TD30是极端气温暖指数,而TNn、TN10p和FD0属于冷指数。6个ETI的详细说明如表1所示。

表1 极端气温指数说明Table 1 Description of extreme temperature indexes
根据逐日气象数据提取了各站点的逐月TXx、TX90p、TNn、TN10p、FD0和TD30。
1.2.2 环流指数的多重共线性分析
选留的100个环流指数之间可能有较高的相关性,因此在建模前需排除相互不独立的环流指数。利用方差膨胀系数(variance inflation factor, VIF)对环流指数进行多重共线性诊断[21]。VIF的计算式为
(1)
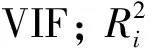
重复多次共线性诊断,逐步剔除VIF>10的具有显著共线性[22]的环流指数。经分析,最终保留了57个环流指数。
1.2.3 关键环流指数的筛选
单站点6个ETI对应的关键环流指数具有差异,但相邻站点关键环流指数较相似,故对各站点进行关键环流指数的筛选,以便用于建模。用Pearson相关系数r表征每个ETI与各环流指数之间的相关程度[23]。初步分析两者关系发现ETI和环流指数之间的相关性基本具有12个月的周期,因此,分别计算滞后0~12个月情况下、各ETI与经过多重共线性分析筛选的57个环流指数之间的r值。r的取值范围是-1~1,r>0(<0)表示正(负)相关,|r|越大相关性越高。根据r的临界值表[24],当显著性水平P<0.01、样本数为720时,r的临界值为0.097,即具有99%显著性水平的关键环流指数的筛选条件为r>0.097。
1.3 ETI模型的建立及模拟
1.3.1 逐步多元线性回归模型(SMLR)
由于ETI与各关键环流指数的相关系数r随滞后时间(月份)变化,因此,取r最大(rmax)时的滞后时间对应的多个关键环流指数进行建模。TX90p、TN10p、FD0和TD30表征极端气温事件发生的频率,单位为d、且只能为正值。SMLR模型采用原始数据得到的模拟值存在负值,因此将各站点TX90p、TN10p、FD0和TD30的序列进行对数转换。以1961—2010年的数据作为率定集,2011—2020年的数据为验证集,建立各对数转换后的ETI序列和特定滞后时间下关键环流指数之间的SMLR模型[25],该模型表示为
y=a1x1,j+a2x2,j+aixi,j+…+anxn,j+b
(2)
式中:y为ETI,其中TXx和TNn采用原始数据,而TX90p、TN10p、FD0和TD30为对数转换后的序列;xi,j为对应rmax的滞后时间为j个月的第i个环流指数;ai为偏回归系数;b为截距。
1.3.2 随机森林RF模型
随机森林模型是通过Bootstrap重抽样构建决策树的组合分类器模型[10],具有良好的分类筛选与预测性能。利用与SMLR模型数量及滞后时间一致的环流指数,对各ETI采用RF建模,以1961—2010年的数据作为率定集,2011—2020年的数据为验证集,并与SMLR模型的建模效果进行比较。
在RF模型训练中需确定2个参数:决策树数量(ntree)和每个树节点上随机变量的数量(mtry)。对于回归问题,ntree一般取500;mtry设置为回归模型所有预测变量数的1/3[26]。RF模型通过均方误差增量(increase in mean squared error, IncMSE)评估变量的重要性,对每棵决策树的输入变量xi进行随机扰动后,检验袋外数据(out of band, OOB)的均方误差,IncMSE值越大表示变量越重要[27],计算公式为
(3)
式中:IncMSEi为第i个变量的IncMSE(%);MSEi1,OOB为未受到扰动的袋外数据的均方误差;MSEi2,OOB为随机扰动后袋外数据的均方误差。
由于模型实际包含的环流指数数量及其重要性在黄河流域80个站点存在差异,因此,提出新的重要性评估指数RankYR(%),以表征各环流指数在整个黄河流域上对极端气温指数的影响程度,表达式为
(4)
式中:Ranki,YR为第i个环流指数的黄河流域总体重要性(%);SIii为站点ii模型实际包含的环流指数的数量;Ranki,ii为第i个环流指数在站点ii中的变量重要性名次;Impi,ii为第i个环流指数在站点ii的变量重要性IncMSE(%);SImax为黄河流域实际包含环流指数最多的站点的环流指数数量。
RankYR值越大,说明该环流指数对整个黄河流域ETI的影响越大,反之亦然。
1.4 模型效果评价
用决定系数(R-square,R2)、林氏一致性相关系数[28](Lin’s concordance correlation coefficient, LCCC)、平均绝对误差(mean absolute error, MAE)以及均方根误差(root mean square error, RMSE)来评估SMLR和RF模型率定和验证的效果。评价指标的计算式为
(5)
(6)
(7)
(8)
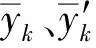
2 结果与分析
2.1 极端气温指数ETI的时空变化
黄河流域1961—2020年6个ETI的年际变化曲线及年极端气温事件的多年平均情况如图2所示。从时间变化来看,极端气温暖指数TXx,TX90p和TD30呈现出波动上升的趋势,说明黄河流域极端高温事件的强度和频率均呈增加趋势,对全球变暖呈正响应。极端气温冷指数FD0、TN10p呈下降趋势,TNn则呈上升趋势,表征黄河流域极端低温事件的发生频率在减小,强度也有所降低。
在空间分布上,由图2可知,TXx、TX90p和TD30的值在黄河流域下游低海拔地区均较高;同时该区域的TNn较大,TN10p和FD0的值则较低,表明该地区极端高温事件的强度和频率均较大,而极端低温事件的强度较弱且频率较低,这可能是受到纬度和地形的影响。总的来说,黄河流域极端高温事件强度和频率的空间分布情况与极端低温事件大致相反。
2.2 关键环流指数及其滞后时间
分析在滞后0~48个月的情况下,ETI与经过多重共线性分析的57个环流指数的Pearson相关系数r的变化,发现其具有明显的周期性,周期为12个月。因此对滞后时间为0~12个月的情况进行具体分析。57个环流指数中大气环流指数共35个,分别是北非副高面积指数(North African Subtropical High Area Index, NAHAI)、西太平洋副高强度指数(Western Pacific Subtropical High Intensity Index, WPSH)、东太平洋副高强度指数(Eastern Pacific Subtropical High Intensity Index, EPSH)、太平洋区极涡强度指数(Pacific Polar Vortex Intensity Index, PPVI)、北大西洋—欧洲区极涡强度指数(Atlantic-European Polar Vortex Intensity Index, AEPVI)、北半球极涡中心经向位置指数(Northern Hemisphere Polar Vortex Central Longitude Index, NVCL)、北半球极涡中心纬向位置指数(Northern Hemisphere Polar Vortex Central Latitude Index, NVCLI)、欧亚经向环流指数(Eurasian Meridional Circulation Index, EMC)、亚洲纬向环流指数(Asian Zonal Circulation Index, AZC)、亚洲经向环流指数(Asian Meridional Circulation Index, AMC)、东亚槽位置指数(East Asian Trough Position Index, EATP)、印缅槽强度指数(India-Burma Trough Intensity Index, IBTI)、北极涛动(Arctic Oscillation, AO)、南极涛动指数(Antarctic Oscillation, AAO)、北大西洋涛动(North Atlantic Oscillation, NAO)、北非—北大西洋—北美副高脊线位置指数(North African-North Atlantic-North American Subtropical High Ridge Position Index, NANRP)、东太平洋副高脊线位置指数(Eastern Pacific Subtropical High Ridge Position Index, EPRP)、南海副高脊线位置指数(South China Sea Subtropical High Ridge Position Index, SSRP)、西太平洋副高西伸脊点指数(Western Pacific Sub Tropical High Western Ridge Point Index, WHWRP)、亚洲区极涡面积指数(Asia Polar Vortex Area Index, APVA)、太平洋区极涡面积指数(Pacific Polar Vortex Area Index, PPVA)、北美区极涡面积指数(North American Polar Vortex Area Index, NAPVA)、大西洋欧洲区极涡面积指数(Atlantic-European Polar Vortex Area Index, AEPVA)、太平洋—北美遥相关型指数(Pacific—North American Pattern, PNA)、东大西洋遥相关型指数(East Atlantic Pattern, EA)、西太平洋遥相关型指数(West Pacific Pattern, WP)、东大西洋—西俄罗斯遥相关型指数(East Atlantic-West Russia Pattern, EAWR)、极地—欧亚遥相关型指数(Polar-Eurasia Pattern, POL)、斯堪的纳维亚遥相关型指数(Scandinavia Pattern, SCA)、50 hPa纬向风指数(50 hPa zonal wind Index, X50ZW)、赤道中东太平洋200 hPa纬向风指数(Mid-Eastern Pacific 200 hPa Zonal Wind Index, MPZW)、850 hPa西太平洋信风指数(West Pacific 850 hPa Trade Wind Index, WPTW)、850 hPa中太平洋信风指数(Central Pacific 850 hPa Trade Wind Index, CPTW)、850 hPa东太平洋信风指数(East Pacific 850 hPa Trade Wind Index, EPTA)和北大西洋—欧洲环流型C型指数(Atlantic-European Circulation C Pattern Index, ACCP)。15个海温指数分别为NINO 1+2区海表温度距平指数(NINO 1+2 SSTA Index, NINO1+2)、NINO W区海表温度距平指数(NINO W SSTA Index, NINOW)、NINO A区海表温度距平指数(NINO A SSTA Index, NINOA)、西太平洋暖池面积指数(Western Pacific Warm Pool Area Index, WPWPA)、大西洋多年代际振荡指数(Atlantic Multi-decadal Oscillation Index, AMO)、亲潮区海温指数(Oyashio Current SST Index, OC)、西风漂流区海温指数(West Wind Drift Current SST Index, WWDC)、NINO B区海表温度距平指数(NINO B SSTA Index, NINOB)、热带南大西洋海温指数(Tropical Southern Atlantic SST Index, TSA)、西半球暖池指数(Western Hemisphere Warm Pool Index, WHWP)、印度洋暖池面积指数(Indian Ocean Warm Pool Area Index, IOWPA)、类ENSO指数(ENSO Modoki Index, EM)、东部型ENSO指数(Nino Eastern Pacific index, NE)、热带印度洋海温偶极子指数(Tropic Indian Ocean Dipole Index, TIOD)和副热带南印度洋偶极子指数(South Indian Ocean Dipole Index, SIOD)。其他指数共7个,分别为西太平洋编号台风数(Western North Pacific Typhoon Number, WNPTN)、登陆中国台风数(Number of Landing Typhoon on China, NLTC)、太阳黑子指数(Total Sunspot Number Index, TSN)、南方涛动指数(Southern Oscillation Index, SOI)、大西洋经向模海温指数(Atlantic Meridional Mode SST Index, AMM)、准两年振荡指数(Quasi-Biennial Oscillation Index, QBO)、大西洋海温三极子指数(North Atlantic Triple index, NAT)。
图3以靖远站TXx为例,对比了在滞后0~12个月的情况下,TXx与经过多重共线性分析的57个环流指数的Pearson相关系数r的变化,其中图3(a)、(b)区分了对TXx具有较大(|rmax|>0.097)和较小(|rmax|<0.097)影响的环流指数组。由图3可知:TXx受到多种环流指数的综合影响,不同环流指数rmax对应的滞后时间不同,大致都在0~12个月的范围内。说明环流指数对TXx的影响存在滞后性,且该滞后效应存在明显的周期性。通过这种方式,在建模过程中可直接剔除图3(b)中的15个环流指数。其他站点的r值各有不同,不再赘述。
进一步对环流指数与TXx在不同滞后时间的Pearson相关关系进行显著性检验,并选择rmax对应的滞后时间,筛选出|r|>0.097且P<0.01的关键环流指数,如图4所示。关键环流指数与TXx在不同滞后时间的|r|的峰值介于0.098~0.893之间,平均为0.441,说明大部分关键环流指数对TXx具有较为显著的影响,rmax对应的滞后时间分别为5、6、11、12个月。其他站点的环流指数滞后时间各有不同,不再赘述。
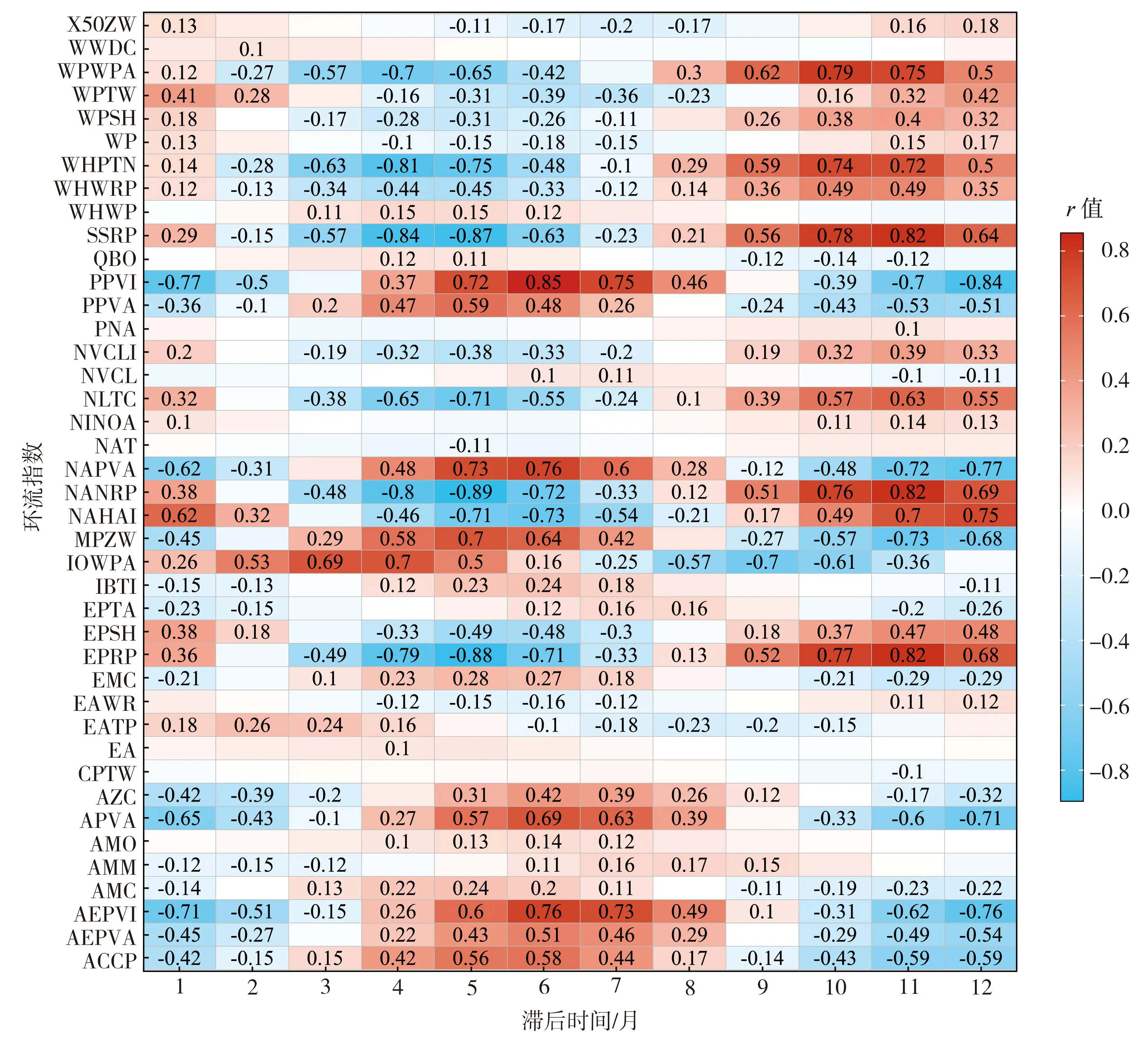
图4 靖远站TXx与关键环流指数在不同滞后时间下的相关系数热图Fig.4 Heat map of correlations between TXx and key circulation indexes at Jingyuan station under different lag times
2.3 模型性能和变量重要性
2.3.1 ETI的对数转换及描述性统计特征
因站点较多,此处以靖远站为例说明4个以d为单位且只能为正值的ETI的原始值及其自然对数转换值的描述性统计特征,如表2所示。TX90p、TD30、TN10p和FD0原始值的偏度系数分别为1.87、1.75、2.25和0.47,峰度系数分别为2.51、1.91、4.09、-1.60,呈现高度正偏态分布且在峰度上偏离正态分布。对原始值进行对数转换后,偏度系数分别为1.09、1.01、1.48、0.09,而峰度系数分别为-0.45、-0.65、0.51、-1.81,说明对数转换值总体上更接近正态分布。其他站点的ETI对数转换序列统计特征有各自的特点,此处不再赘述。

表2 靖远站TX90p、TD30、TN10p和FD0的原始值及其自然对数转换值的描述性统计Table 2 Descriptive statistics of original values and natural logarithmic values for TX90p, TD30, TN10p and FD0 at Jingyuan station
2.3.2 建立的SMLR模型参数特征
基于筛选的关键环流指数进行SMLR模型建模,并对黄河流域各站点的ETI进行了模拟,得到具体方程,以靖远站为例展示了SMLR模型中对应关键环流指数的偏回归系数以及ETI与环流指数之间的相关性为rmax时对应的滞后月数,如表3所示。TX90p和TD30与各环流指数的rmax对应的滞后时间完全相同。TXx和TNn及FD0和TN10p与环流指数的rmax对应的滞后时间也较为接近,与TX90p和TD30的rmax对应的滞后时间接近或间隔6个月。其他站SMLR模型的参数特征也已经获得,不再赘述。
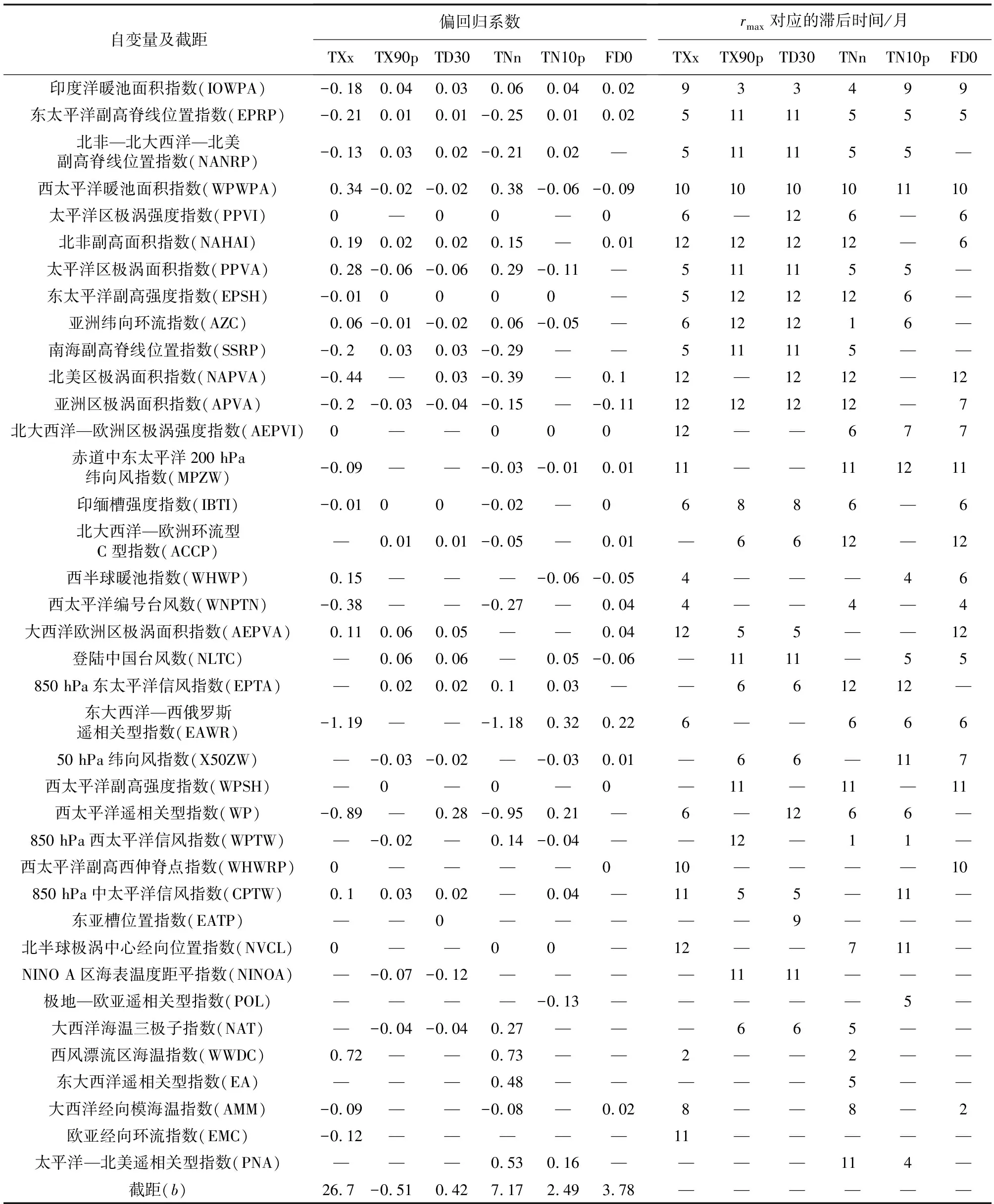
表3 靖远站逐步多元线性回归模型方程的偏回归系数、截距及rmax对应的滞后时间Table 3 Partial regression coefficient, intercept and the lag time for obtaining the maximum value of r in SMLR model equation at Jingyuan station
2.3.3 基于RF的环流指数重要性排序
以靖远站为例,基于RF模型获得的环流指数的重要性IncMSE排序如图5所示。环流指数对6个ETI的影响程度均不同,其中太平洋区极涡强度指数(PPVI)是影响TNn和FD0的最重要指数,印度洋暖池面积指数(IOWPA)则是影响TX90p和TD30的最重要指数,北大西洋—欧洲区极涡强度指数(AEPVI)和北非—北大西洋—北美副高脊线位置指数(NANRP)分别是影响TXx和TN10p的最重要指数。太平洋区极涡强度指数(PPVI)、北非—北大西洋—北美副高脊线位置指数(NANRP)、南海副高脊线位置指数(SSRP)、东太平洋副高脊线位置指数(EPRP)和北非副高面积指数(NAHAI)对ETI的重要性排序最靠前。其他站的重要性排序结果也已获得(数据略)。
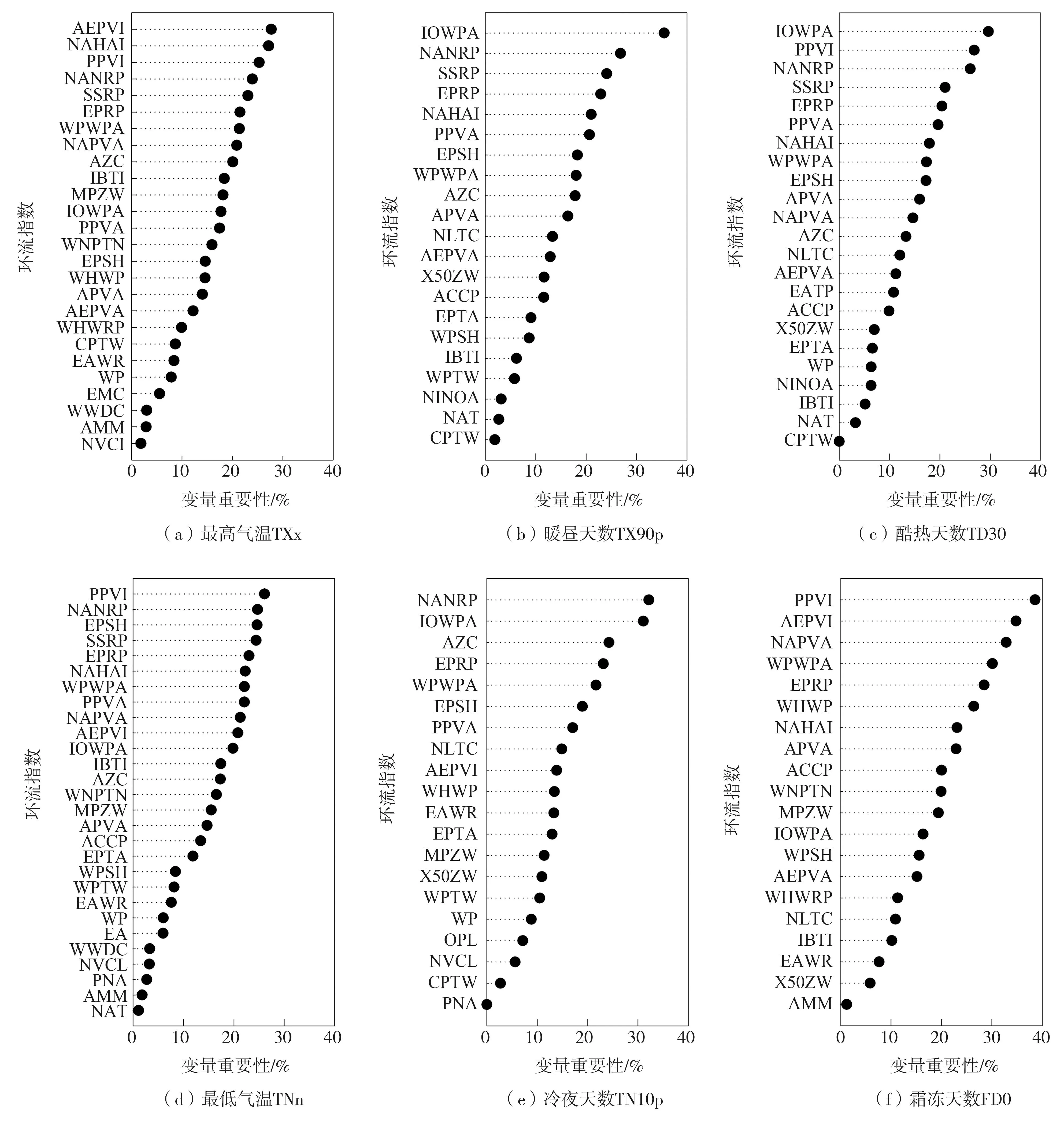
图5 靖远站影响极端气温指数的环流指数的重要性排序Fig.5 Rank of importance of circulation indexes influencing extreme temperature indexes at Jingyuan station
IncMSE仅体现环流指数在单站点的重要性,RankYR考虑了黄河流域全部80个站点上选取的关键环流指数对ETI的重要性。黄河流域RankYR>5%的环流指数如表4所示。PPVI是影响黄河流域TXx、TNn、TX90p和FD0的最重要的环流因子;NANRP对黄河流域TN10p和TD30的影响最大。

表4 影响黄河流域各极端气温指数的环流指数重要性RankYRTable 4 RankYR of circulation indexes affecting extreme temperature indexes in the Yellow River Basin %
2.3.4 模型性能评价
SMLR模型和RF模型模拟的黄河流域80个站点的ETI值的率定和验证结果如图6所示。由图可知:①在率定期,SMLR和RF模型R2的中位数变化范围是74.7%~95.4%和74.4%~95.9%;LCCC中位数的变化范围是0.83~0.98和0.78~0.98。SMLR模型MAE中位数的变化范围是1.6~1.8 ℃和1.3~2.3 d,而RF的是1.6~1.8 ℃和1.3~2.2 d。SMLR模型RMSE的中位数变化范围是2.1~2.3 ℃和2.7~4.0 d,RF模型的是2.0~2.3 ℃和2.8~3.5 d。②在验证期,SMLR和RF模型分别解释了ETI变化的53.4%~94.6%和64.3%~95.4%;而LCCC中位数的变化范围是0.71~0.97和0.69~0.97。SMLR模型的MAE中位数的变化范围是1.7~1.8 ℃和1.5~2.9 d,而RF模型的是1.7~1.9 ℃和1.5~3 d。SMLR模型RMSE的中位数变化范围是2.2~2.3 ℃和3.3~4.7 d,而RF模型的是2.1~2.3 ℃和2.8~4.4 d。2种模型对ETI的预测能力都比较好,其中RF模型模拟TNn的R2、LCCC、MAE和RMSE均优于SMLR模型。RF模型模拟TX90p、TD30和TN10p时仅LCCC稍差,其他情况下RF模型均优于SMLR模型。而RF模型模拟FD0的R2明显优于SMLR模型,LCCC、MAE、RMSE则略微差于SMLR模型。SMLR模型仅模拟6个ETI中TXx的效果优于RF模型。③总的来说,RF模型的模拟效果优于SMLR模型。验证期2个模型模拟ETI的R2,LCCC,MAE和RMSE的表现整体上略低于率定期,但未出现明显的模拟性能下降,且RF模型模拟TN10p的MAE和RMSE在验证期的表现略优于率定期。
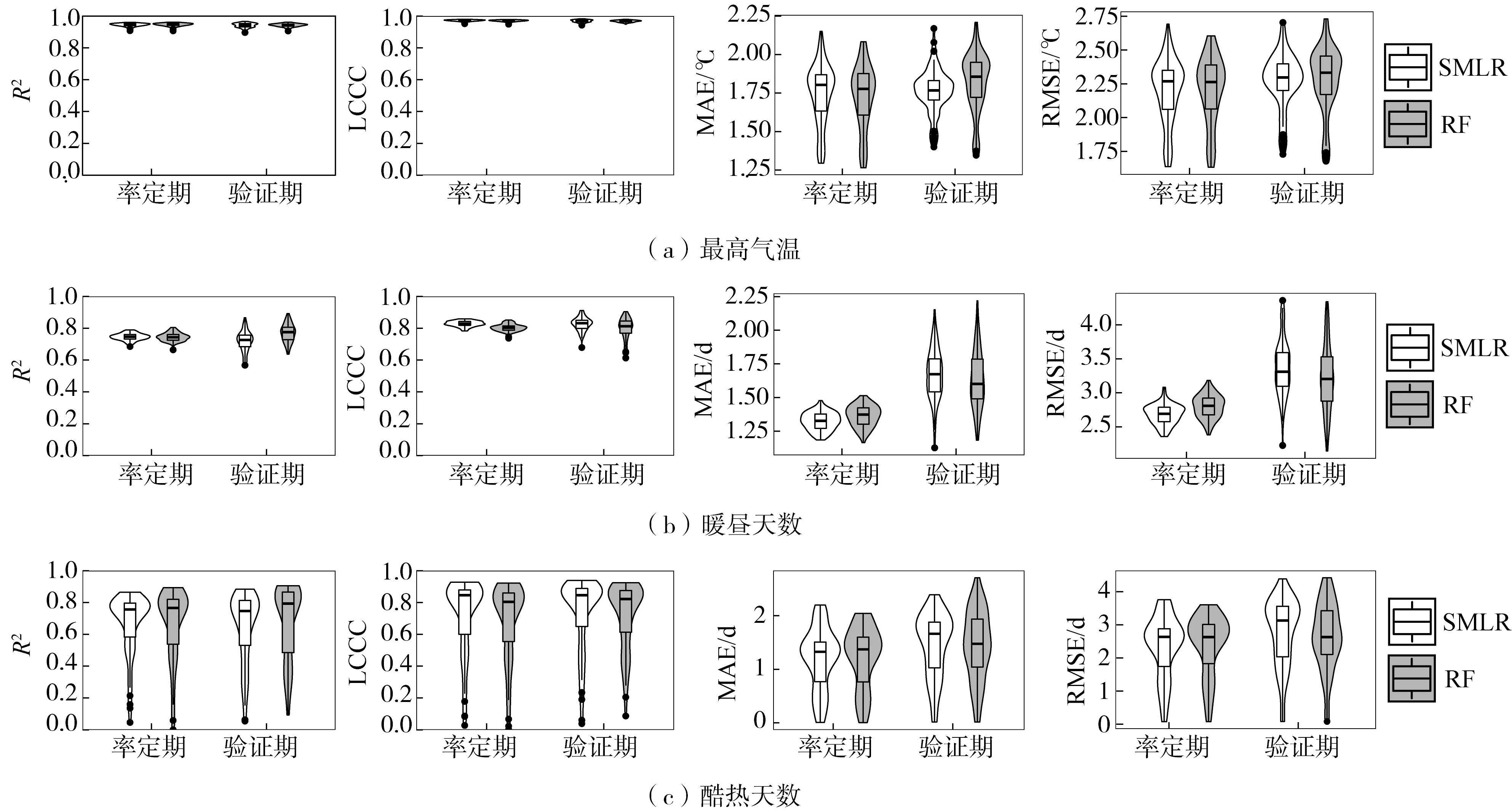
图6 逐步多元线性回归和随机森林模型在黄河流域80个站点模拟极端气温指数的率定和验证结果Fig.6 Calibrated and validated results of each extreme temperature index simulated by the SMLR and RF models at 80 sites in the Yellow River Basin
2.4 极端气温指数的预测
由于RF模型模拟ETI的性能总体优于SMLR模型,且各环流指数对黄河流域极端气温指数的影响具有0~12个月的时滞特征,故基于RF模型利用2021年10月—2022年10月的环流指数数据预测了2022年11月黄河流域80个站点的ETI,其空间分布如图7所示。由图可知:2022年11月,极端高温事件的强度(TXx)和发生频率(TX90p和TD30)较高的站点主要集中在流域下游的低海拔地区和局部河谷地带。极端低温事件的频率指数(TN10p、FD0)与极端高温事件的频率指数(TX90p、TD30)空间分布规律基本相反;TNn和TXx的空间分布特征基本相同,最低气温(TNn)越小,表征极端低温事件的强度越大,即极端高温事件与极端低温事件的强度具有相反的空间分布规律。总体上,预测的2022年11月黄河流域各ETI的空间分布情况与多年平均情况相似。待新的环流指数更新后,可采用类似方法对黄河流域多站点的ETI进行实时动态预测,从而对流域未来极端气温事件进行预警。
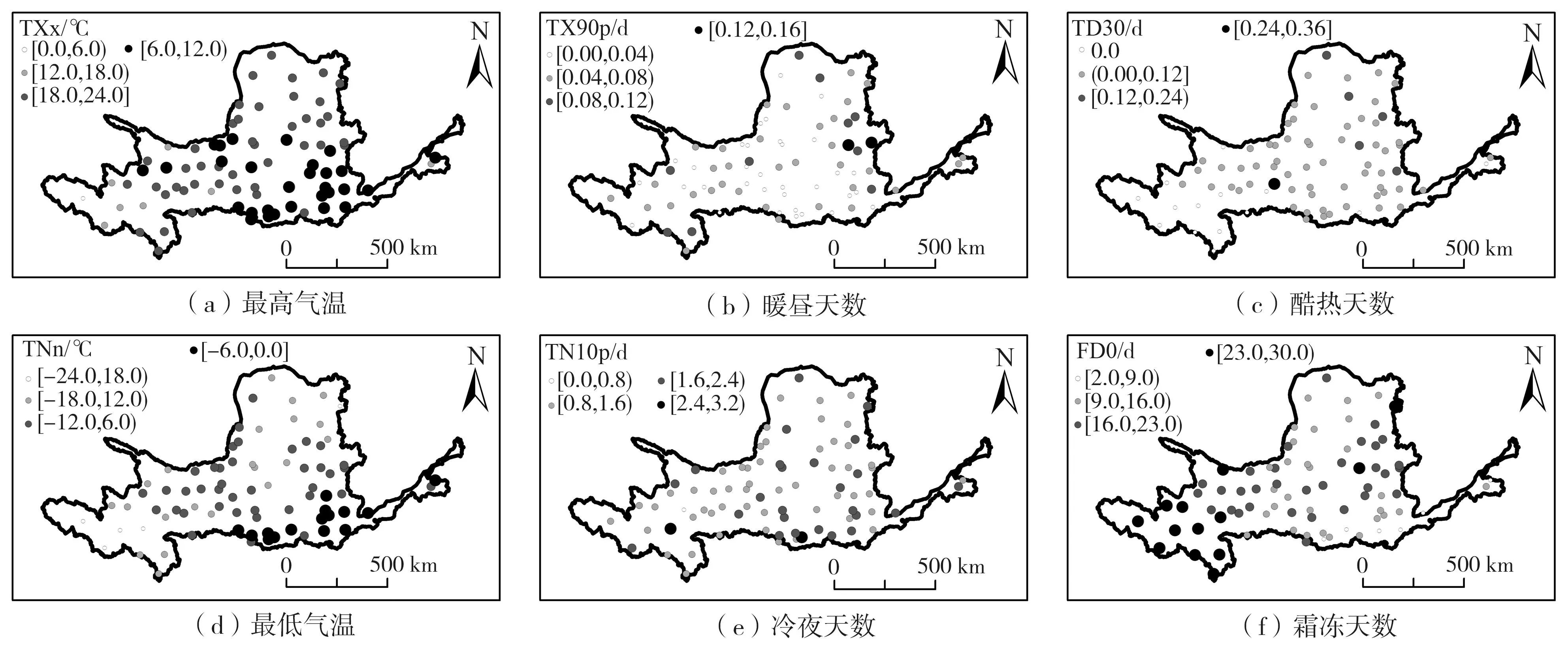
图7 基于随机森林模型预测的2022年11月黄河流域极端气温指数Fig.7 Forecasted extreme temperature indexes in November 2022 based on the RF models established in the Yellow River Basin
3 讨论
极端气温事件受多种大气环流因子的综合影响。丁之勇等[14]发现我国北疆地区极端气温指数受AO的影响最大,其次是NAO,而ENSO对其影响较小。龚道溢等[29]认为NAO主要影响北美、西欧以及北非个别地区的气温,北太平洋涛动(north Pacific oscillation, NPO)主要影响北太平洋和北美个别地区的气温,南方涛动指数(SOI)则主要对太平洋热带地区气温产生影响。但过去研究多集中于单个或几个环流指数对研究区域内极端气温事件的影响,而本研究筛选了对极端气温事件有显著影响的多个环流指数,充分探究极端气温事件对多种大气环流因子的综合响应,本文从130个环流指数中,通过数据预处理、VIF多重共线性分析、考虑滞后性的Pearson相关分析及显著性检验等方法,严格地筛选出6个ETI的关键环流指数,最终构建SMLR和RF模型并进行环流指数重要性排序,克服了大气环流因子选取不客观、不全面的局限性。
大气环流对极端气温的影响具有滞后性。汪宁等[30]研究发现我国北部、东北部、南部地区的气温和降水对欧亚遥相关型的响应约有2~4 d的滞后时间。黄浩等[31]发现AO和ENSO对河东地区冬、夏两季的极端气温指数有显著影响,且呈现出0~1 a的时滞特征。马乃孚等[32]提出北太平洋海温与华中夏季气温存在较好的滞后相关关系,通过赤道东太平洋海温异常预测华中地区夏季气温的可预报尺度为1~3个月。本文发现环流指数对黄河流域极端气温指数的影响具有0~12个月的时滞特征,且不同环流指数的最佳滞后时间也有差异,这与黄浩等[31]的结果部分一致。同时本研究以时滞特征为切入点计算了不同环流指数的最佳滞后时间,并通过最佳滞后时间序列数据建立模型预测了黄河流域ETI,考虑了环流指数对ETI影响的时滞性,从而提高了模拟的效率和精度。
黄河流域ETI影响因子的重要性在不同站点上具有差异。RF模型具有良好的模拟性能,已被应用于很多领域。本研究采用2种模型对黄河流域ETI进行实时预测,对比分析发现在相同输入下,RF模型除对TXx的模拟效果稍弱外,对其他5个ETI的模拟效果均优于SMLR模型。由于RF模型能够给出单个站点的变量重要性排序,且环流对ETI的影响具有区域差异[33],本文基于RF模型给出的变量重要性指数IncMSE,创新性地提出了影响整个黄河流域80个站点的各ETI的环流指数重要性排序方法RankYR,并进行了具体分析,从而扩展了重要性排序的应用领域,得出了对黄河流域极端气温事件提供准确可靠预报的新方法,为将来研究分析黄河流域气候变化中极端气温变化可能造成的影响提供了参考。
4 结论
本文基于关键环流指数的最佳滞后时间序列数据构建了6个极端气温指数的SMLR和RF模型,探究了极端气温事件对多种大气环流因子的综合响应,得出以下结论:
1)黄河流域1961—2020年的ETI中,TXx、TX90p、TD30和TNn呈波动上升的趋势,而TN10p和FD0呈现下降趋势;极端高温事件的强度和发生频率的空间分布特征与极端低温事件基本相反。
2)以靖远站TXx为例,极端气温事件受多种环流指数的综合影响。环流指数对TXx的影响存在滞后性和明显的周期性。关键环流指数对极端气温指标具有显著影响,其rmax对应的滞后时间主要为5、6、11和12个月。同时,环流指数对ETI的影响程度存在差异,PPVI对TNn和FD0的影响最大,IOWPA对TX90p和TD30影响最大,AEPVI和NANRP对TXx和TN10p影响最大。对整个黄河流域来说,PPVI对TXx、TNn、TX90p和FD0影响最大,而NANRP对TN10p和TD30影响最大。
3)SMLR和RF模型对ETI的预测能力较好,验证期R2分别为0.53~0.95和0.64~0.95。RF模型除对TXx的模拟效果稍差外,对其他5个ETI的模拟效果均优于SMLR模型,因此被选择用于预测黄河流域多站点的实时ETI。预测的2022年11月,黄河流域ETI的空间分布特征与多年平均情况基本相似。极端高温事件的强度(TXx)和发生频率(TX90p和TD30)较高的站点主要集中在流域下游的低海拔地区和局部河谷地带,极端低温事件强度和发生频率的空间分布规律与基本极端高温事件相反。
