某地铁转向架构架端部开裂机理及分析

李 飞，吴兴文，罗 贇，刘开成，谢晨希

（西南交通大学 牵引动力国家重点实验室，成都 610031）

地铁作为城市轨道交通的重要交通工具，具有运量大、准时、安全等一系列优点［1］，近年来随着地铁运营公司行车密度及地铁车辆运量的提高，加速了地铁线路的恶化，更容易出现钢轨波磨、车轮多边形磨耗等轮轨短波不平顺。这些轮轨短波不平顺极易导致轮轨高频激励，从而导致结构高频共振疲劳问题。

国内学者针对轮轨短波不平顺引发结构振动疲劳问题做了大量理论和试验研究工作。连青林等［2］针对客车转向架安全吊座孔附近产生的疲劳裂纹问题进行了有限元分析和线路试验，结果表明轮轨冲击频率与安全吊杆振动频率相近，从而导致共振疲劳失效问题。石怀龙等［3］针对地铁车辆轴箱吊耳断裂问题采用线路试验开展断裂机理研究；通过分析振动激扰源和结构响应特性，发现波长为61.5 mm 钢轨波磨是导致车辆振动水平激增的主要原因，同时钢轨波磨通过频率在吊耳固有模态频带内，进一步导致结构共振从而引发疲劳破坏；作者同时提出钢轨打磨、优化吊耳结构设计和使用管理条件等解决措施。何伟等［4］针对某地铁线路车辆在运行中出现一系钢弹簧疲劳断裂的现象，建立了一系钢弹簧柔性的刚柔耦合动力学模型，结果表明地铁车辆车轮多边形的阶次、波深以及列车的运行速度对一系钢弹簧的疲劳寿命都有很大的影响，且当车轮多边形磨耗通过频率与一系钢弹簧固有频率接近时，其寿命显著降低。覃才等［5］针对某型高速动车组吊耳装置异常振动且个别出现明显疲劳裂纹问题，采用有限元法建立吊耳装置有限元分析模型，分析吊耳装置的振动特性、应力特性和疲劳寿命，研究吊耳装置的厚度和倒圆角半径对其振动特性、应力水平和疲劳寿命的影响，为吊耳装置的设计提供参数范围。

文中针对某地铁车辆转向架构架端部开裂问题，采用线路试验的方法，从时域和频域的角度分析振动激扰源和轴箱、构架端部的响应特性，确定了构架端部开裂原因；同时进一步通过试验手段验证了改进方案的效果。

1 构架端部开裂现象

研究对象为某B 型地铁转向架构架端部，其在运营过程中出现了多起疲劳失效问题，如图1 所示。该转向架构架端部为悬臂梁结构，主要用于安装轮喷装置和天线梁等附属部件；对于没有安装附属部件的构架端部，则为明显的悬臂梁结构。通过对失效部位的分析，所有端部的失效位置均为悬臂梁与构架下盖板的T 型焊接接头处。在实际运营过程中，该位置可能承受从一系悬挂（钢弹簧和一系液压垂向减振器）传递的轮轨高频激励，从而激发构架端部悬臂结构的模态振动。

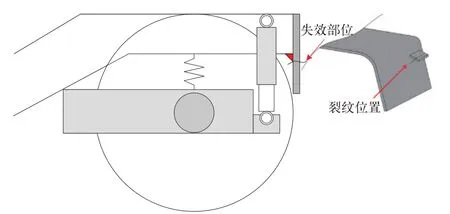
图1 构架端部开裂位置

为了弄清构架端部失效原因，应该首先弄清转向架构架整体模态和构架端部局部模态之间的关系，转向架一系悬挂系统高频振动传递特性，以及构架端部振动加速度与端部关键位置动应力之间的关系；同时还需要揭示转向架构架端部振动与轮轨表面状态之间的关联关系。为此，通过线路实测方法，测试了转向架构架振动加速度和关键部位动应力数据，以及典型线路区段的钢轨表面状态。试验数据表明，该转向架车轮表面状态较好，没有明显的车轮多边形磨耗，因此需要重点关注钢轨表面状态—轮轨高频激励—构架端部失效的相互关联。

2 转向架构架工作模态研究

转向架构架工作模态为构架在外部激励条件下表现出来的响应模态，其反映了构架在实际服役过程中主要表现的模态或者振动模式，对结构的失效分析具有重要意义。为此文中基于Poly-MAX 方法，利用加速度传感器对转向架构架工作模态进行了识别。

PolyMAX 方法是多参考点最小二乘复频域法的扩展，利用输出响应的功率谱密度近似代替频响函数，使用极大似然估计使误差最小化，实现全局模态的识别，有很好的抗干扰能力［6］。PolyMAX方法主要分为以下3 步［7-9］：

（1）建立线性化的直交矩阵模型。频域系统中频响函数H(ω)与输入参数矩阵F(ω)和输出参数矩阵X(ω) 之间的关系可以表示为式（1）～式（4）［7-8］：

式中：m为输入通道总数；l为输出通道总数；Δt为采样间隔；ω为角频率；Z为多项式基函数；P为数学模型的阶次；αr，βr分别为分母和分子矩阵的多项式系数，可由最小二乘法求得。

（2）求解极点和模态参与因子。在上述求得分母矩阵系数αr的基础上对其扩展的酉矩阵进行特征值分解，可得系统的极点及模态参与因子为式（5）：

式中：V为特征向量矩阵；Λ为酉矩阵的特征值矩阵（对角矩阵），其对角元素λi(i=1，2，…，mP)与系统极点Pi和间存在的关系为式（6）：

而模态阻尼比为式（7）：

式中：ξi为阻尼比；σi为阻尼因子；ωi为无阻尼系统得固有频率；ωdi为有阻尼系统固有频率。

取特征向量矩阵[V]mP×mP最下面的m行，构成的子矩阵就是模态参与因子矩阵[L]mP×mP。

（3）获取模态振型。采用最小二乘频域法（FSFD）求解模态振型，其拟合函数为式（8）：

式中：[H(ω) ]l×m为测量的频响函数矩阵；ψi为待求的第i阶模态振型列向量；＜l＞为模态参预因子行向量；LR和UR分别为分析频带外模态影响的下残余项和上残余项矩阵。

前文已求出极点Pi和模态参预因子向量＜l＞，故H(ω)可按不同采样频率列方程，最后通过线性最小二乘估计求得未知的模态振型ψi(i=1，2…，N)，以及上下残余项矩阵LR和UR。

为了获得更加准确的构架端部运营模态，在构架主体粘贴29 个三向振动加速度传感器，如图2所示。截取车辆在典型区间内构架振动测点的加速度数据，获取其频响函数，然后基于PolyMAX 方法求解构架模态的稳态图如图3 所示。图中o 表示未找到极点；v 表示频率和模态参预因子稳定；f表示在给定精度内频率稳定；d 表示频率和阻尼稳定；s 表示3 种参数全部稳定［10］。

图2 构架振动测点简图

图3 稳态图

综合多个工况下的识别结果，识别出构架主要模态参数和振型见表1，其中构架端部存在频率为222.9 Hz，阻尼比为0.72% 的纵向摆动固有模态。固有模态如图4 所示。

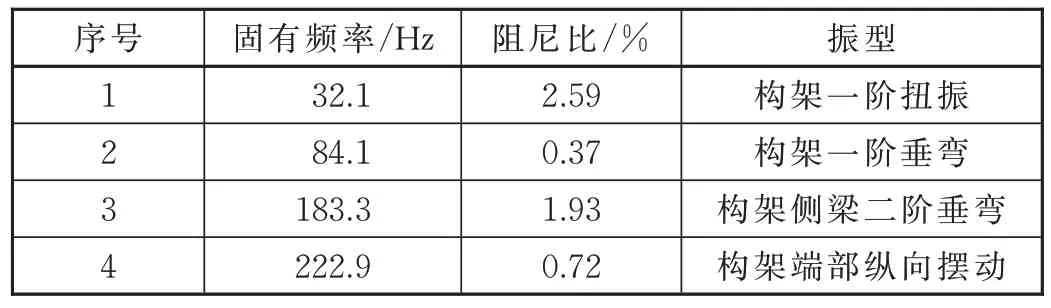
表1 转向架构架主要模态参数及振型

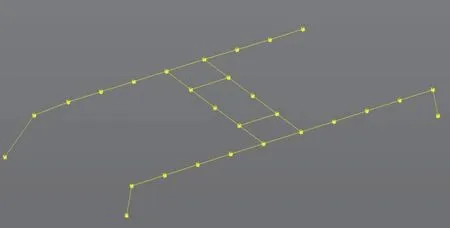
图4 构架端部摆动模态

3 转向架构架端部失效分析

3.1 试验方案

对该型地铁车辆进行线路跟踪测试，车辆在AW3 即重车状态下在运营线上进行试验，列车采用自动驾驶模式ATO 速度运行，常用速度为60 km/h，最大速度不超过120 km/h。由于轴箱振动加速度大小能够很好地反映线路激扰水平，构架端部振动加速度和裂纹区域应力状态能够直接表明激扰对开裂区域的影响，故在轴箱和构架端部安装加速度传感器以获取加速度时域数据；并在裂纹区域粘贴应变片，获取关注部位动应力数据。加速度传感器、应变片测点位置如图5 所示，这些加速度和动应力信号最终通过信号线汇集在终端采集系统。

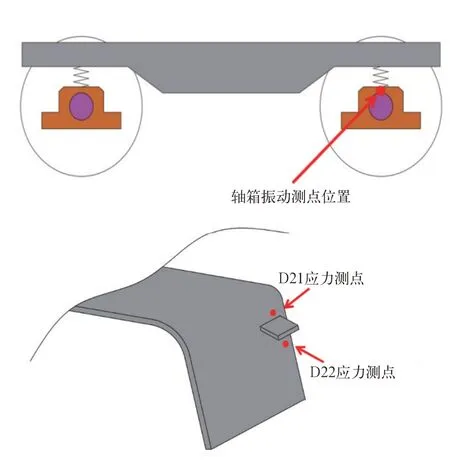
图5 构架振动和动应力测点简图

3.2 时频特征分析

选取轴箱振动加速度较大的某个区间作为典型区间进行分析。该区间轨道类型主要包括普通短轨枕整体道床和弹性短轨枕两种。典型区间内轴箱垂向和构架端部纵向振动加速度时频图如图6、图7 所示，由图可知18 mm 弹性短轨枕区段60～80 s 内振动加速度明显大于其他区段，其中18 mm弹性短轨枕区段振动加速度较大区段频带范围为190～230 Hz，普通短轨枕区段振动加速度较大区段频带范围为80～100 Hz，其余区段振动能量较弱，对构架疲劳破坏影响较小。对弹性短轨枕区段60～75 s 内轴箱振动垂向和构架端部纵向加速度时域数据进行频谱分析得其主频分别为212.3 Hz和221.1 Hz。

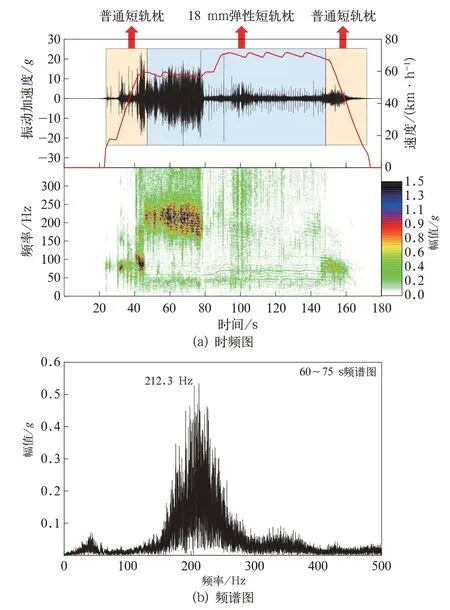
图6 轴箱垂向振动加速度特征

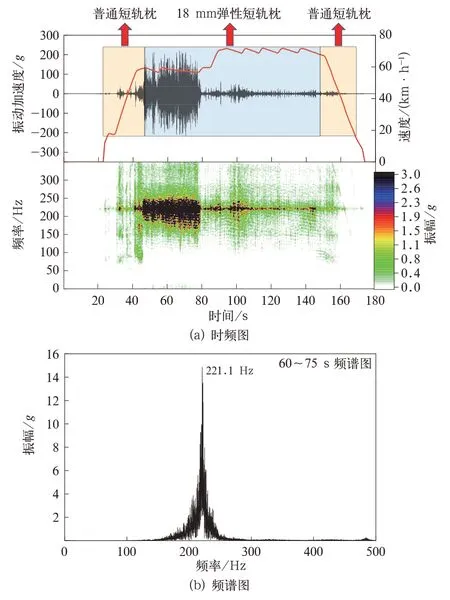
图7 构架端部纵向振动加速度特征

构架端部裂纹区域两个应力测点处的动应力时程曲线和高应力区段的频谱如图8、图9 所示，其中18 mm 弹性短轨枕区段60～75 s 内动应力幅值明显大于其他区段，应力范围超过180 MPa，且频次较多，表明该区域处于高应力水平，其他区段应力幅值较小，对高应力时段信号进行频谱分析发现裂纹区域测点信号主频均为221 Hz 左右。

图8 构架端部D21 应力测点时频图

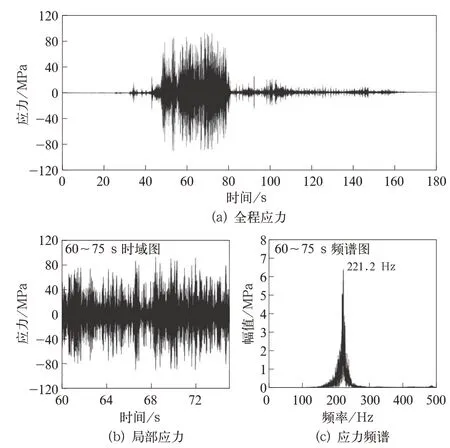
图9 构架端部D22 应力测点时频图

对典型区间进行轨道调查，发现弹性短轨枕区段存在波长为80 mm 左右、波深为0.2 mm 左右的钢轨波磨如图10 所示，且波磨区段占弹性短轨枕区段总长的33%，其余弹性短轨枕区段无明显钢轨波磨。普通短轨枕区段存在波长为200 mm 左右的钢轨波磨，但幅值较小，占比较低。已知该区段车速常用速度为60 km/h，由公式f=v/l可得波长为80 mm 的钢轨波磨通过频率为208.3 Hz，由此可见波磨通过频率与轴箱垂向振动加速度主频和构架端部纵向加速度主频接近，说明来自线路波长为80 mm 的钢轨波磨激扰通过轴箱传递到构架端部，并与构架端部固有频率222.9 Hz 共振，引发构架端部振动疲劳问题。

图10 轨道不平顺曲线图

4 构架端部改进效果分析

4.1 构架端部安装加强筋

由上述数据分析可知，构架端部固有频率与钢轨波磨通过频率共振引发构架端部疲劳破环。为了抑制构架端部纵向振动，在构架端部安装加强筋并在同一线路相同工况下对改进后车辆进行线路测试，如图11 所示。统计全线15 个区间构架端部纵向振动加速度水平，对每个站间加速度时间历程进行0.2 s 滑移峰值计算，计算每个窗口内99.85%可靠度下的峰值，再取最大值，得到站间的最大值，构架端部改进前后加速度最值对比如图12 所示。安装加强筋前后典型区间内构架端部测点动应力和加速度时域数据对比如图13～图15 所录，发现安装加强筋后可以显著降低端部纵向振动加速度和动应力。对改进方案60～75 s 内的实测数据进行频谱分析，如图16～图18 所示，发现安装加强筋后构架端部振动加速度和动应力主频由原方案的221 Hz 左右下降到190 Hz 左右，能量降低90%以上，说明改进方案效果明显。

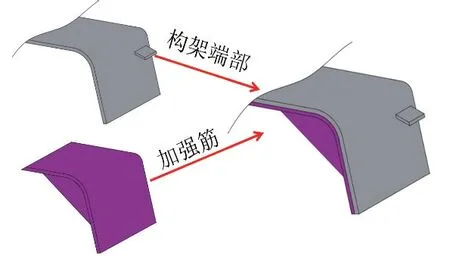
图11 构架端部安装加强筋

图12 构架端部纵向振动加速度区间最值对比

图13 构架端部应力D21 测点对比

图14 构架端部应力D22 测点对比

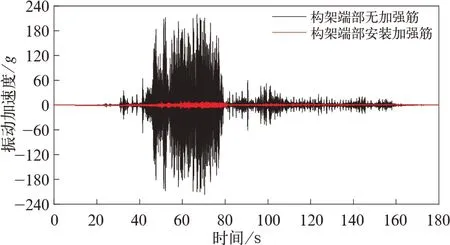
图15 构架端部纵向振动加速度对比

图16 改进方案D21 应力测点频谱图对比

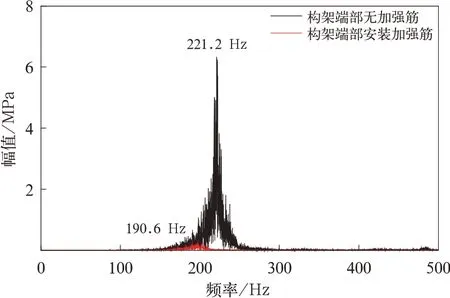
图17 改进方案D22 应力测点频谱图对比

图18 改进方案构架端部纵向加速度频谱图对比

4.2 疲劳损伤评估

损伤是用来表征载荷作用对材料造成的伤害，通常认为结构在承受疲劳载荷的情况下损伤是逐渐累积的，文中基于实测数据对构架端部关键测点的动应力数据进行疲劳损伤分析。

首先对实测得到的动应力数据进行数据处理，去掉异常点和零飘，再基于雨流计数法对实测的动应力数据进行统计，得到对应测点的循环次数和应力范围，然后以累积频次为横坐标，应力范围为纵坐标，最终得到测点应力谱如图19、图20 所示，改进方案与原始方案总累计频次值接近，但改进方案应力范围大幅减小。最后基于Miner 线性损伤累计理论，参照结构焊接接头的S-N曲线进行损伤计算。

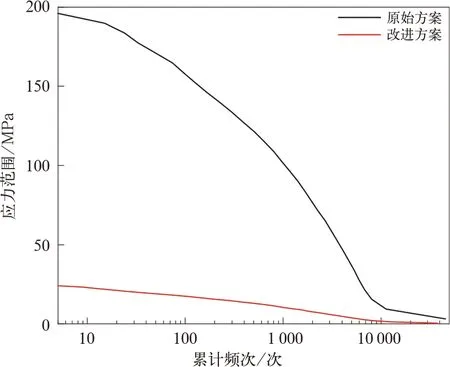
图19 D21 测点改进前后应力谱对比

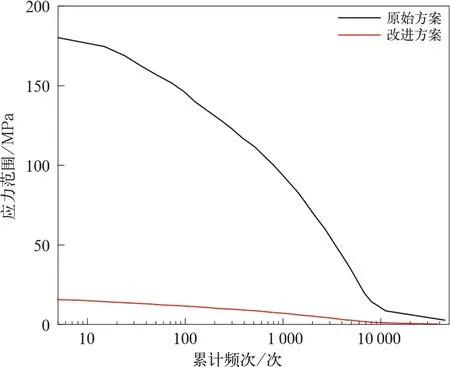
图20 D22 测点改进前后应力谱对比

由于构架端部的失效位置均为T 型焊接接头，根据IIW 国际焊接学会提供的S-N曲线，选取T 型接头对应的S-N曲线，2×106次循环对应的应力循环范围为80 MPa；循环次数小于107次时，S-N曲线斜率m=3；同时考虑小载荷对高周疲劳的影响，对于循环次数大于107次时，S-N曲线斜率m=5，S-N曲线如图21 所示。

图21 S-N 曲线

Miner 累计损伤理论：在任何应力循环作用下结构都会产生疲劳损伤，疲劳损伤程度与应力幅作用的频次有关，与载荷谱加载历程、加载方式无关，应力加载所造成的损伤增量可线性叠加。对应的损伤可以表示为式（9）：

结合IIW 标准给出的材料S-N曲线和Miner 线性累计损伤法则可得式（10）：

式中：ni为载荷谱中应力范围Δσi的循环次数；Ni为在该应力范围时将导致损坏的循环总数；m、C为材料S-N曲线参数。当总的损伤D=1 时，结构发生破坏。

将Miner 线性累计损伤理论公式转化为里程公式，可得式（11）：

式中：L为安全运行公里数；L1为实测公里数。

构架端部动应力测点损伤对比如图22 所示，结果表明：安装加强筋后构架端部测点损伤值大幅降低，满足转向架的使用寿命要求。

图22 构架端部动应力测点损伤对比

5 结论

针对某B 型地铁车辆转向架构架端部开裂问题开展运营模态分析和线路试验研究，分析了构架端部开裂原因及改进方案效果。结论表明：

（1）基于PolyMAX 方法识别出构架在实际运营的工作模态，其中构架端部存在频率为222.9 Hz、阻尼比为0.72%的纵向局部摆动模态。其与弹性短轨枕区域波长80 mm 通过频率为200 Hz 左右的钢轨波磨激励频率会发生耦合共振，从而导致局部路段构架端部振动加剧，关键位置动应力增加，进一步导致构架端部振动疲劳问题。

（2）构架端部安装加强筋后使构架端部局部刚度和阻尼比增加，在相同工况条件下改进后结构振动加速度和动应力均比原方案减小90% 左右，使得改进方案损伤显著减小，满足转向架的使用寿命要求。