民用航空运输载重配平问题研究综述

赵向领，左 蕾，李云飞，徐吉辉

（1.中国民航大学空中交通管理学院，天津 300300，2.空军工程大学装备管理与无人机工程学院，西安 710051）

飞机的载重平衡是与民用航空货运直接相关的运行保障工作之一。配载员根据实际运输需求把装载好的不同类型集装器（ULD，unit loading devices）分配到飞机的不同机舱位置，确保飞机重心在合理范围之内，并尽量减少燃油成本，增大运输效益[1]。

飞机载重平衡的合理性是影响飞机安全高效运行的重要因素之一[2]。飞机载重平衡不合理将会导致严重的后果，如在起飞中，飞机重心太靠后会容易造成飞机抬前轮时攻角过大，从而引起机尾擦地；飞机重心太靠前易造成飞机驾驶杆力过大，飞机滑跑距离过长，造成跑道长度不够用。在飞行中，重心配置不均衡会导致飞机飞行姿态控制困难，遇到颠簸气流极易触发风险并增加操控难度，产生难以预料的严重后果。鉴于此，做好飞机配载平衡，对于避免飞行事故极为重要。

合理的载重平衡计划对航空公司降低燃油消耗及运营成本和提高运营效率均有很大帮助[3]。一架B737-800 飞机在26 000 ft（1 ft=0.304 8 m）的航行高度和0.6 马赫的飞行条件下，飞机重心从22%平均空气动力弦（MAC，mean aerodynamic chord）转变到24%MAC 时，可以降低0.05%的阻力，大约可以减少0.05%的耗油量。由此可见，合理的飞机载重平衡可带来更好的节油效果。

在实际操作中，多数航空公司使用相关图表和软件进行配载计算，然而这些图表和软件大多用于计算重心和约束，失去了大量优化装载和降低燃油消耗的机会。更重要的是，配载通常在飞机起飞前1 h 进行规划和实施，时间有限。对于复杂的货运配载，由于航空公司配载员手工操作能力有限，因配载造成航班延误的事情时有发生。因此，对飞机的载重与平衡计划进行及时优化不仅可以提高航班运行效率，还能让飞机在使用更少油量的情况下飞行得更安全。

在学术研究方面，飞机的载重平衡问题是典型的NP 难题（NP-hard problem）[4]。货物装载计划的困难会随货舱分舱的大小和航段数量的增加而增大。在新冠肺炎疫情期间，多数航空公司采取“客改货”的方式进行货物运输，客改货飞机在载重平衡上与货机有着很大不同，客改货飞机主货舱用于装载ULD 属于指派问题，而下货舱装载散货属于装箱问题，因此，客改货飞机的载重平衡问题属于指派问题和装箱问题的组合优化问题。

因此，有必要对民用航空运输配载的发展和研究方法进行研究。本文致力于从学术角度整理配载的研究过程，在研究前人成果的基础上，提出未来的配载技术将以实际重心包线为基础，由枚举法过渡到整数规划方法，逐步实现配载优化，并借助机器学习等技术实现属于航空公司偏好的智能配载方案。

1 载重平衡的基本问题

1.1 重量

飞机各部分所受重力的合力称为飞机的重力（简称重量）。重量约束是飞机安全运行的最重要约束之一。飞机总重量W 包括3 部分：营运空机重量（OEW，operation empty weight），业载（PL，pay load）重量和燃油（fuel）重量，飞机总重量可表示如下

式中：WOEW表示营运空机重量；WPL表示业载重量，即旅客、货物、行李等运输重量之和；Wfuel表示燃油重量。

根据装载的燃油量，飞机重量可以分为3 种情况：起飞重量（TOW，takeoff weight）、着陆重量（LW，landing weight）和无油重量（ZFW，zero fuel weight）。由起飞油量（TOF，takeoff fuel）和航段耗油量（TripF，trip fuel）可得

式中：WTOW表示起飞重量；WLW表示着陆重量；WZFW表示无油重量；WTOF表示起飞油量重量；WTripF表示航段耗油重量。

飞机的起飞重量、着陆重量和无油重量，分别受到其最大重量限制，其中最大起飞重量（MTOW，maximum takeoff weight），最大着陆重量（MLW，maximum landing weight），最大无油重量（MZFW，maximumzerofuelweight）三者有如下限制关系

式中：WMZFW表示最大无油重量；WMTOW表示最大起飞重量；WMLW表示最大着陆重量。

根据式（1）～（3）可计算出飞机的3 个可用业载重量，即基于MTOW 限制的飞机最大业载WMPL1、基于MLW 限制的飞机最大业载WMPL2和基于MZFW 限制的飞机最大业载WMPL3，由于3 种重量是不同方面对重量的约束，所以计算出的最大业载也不相同，本文选择最小业载作为飞机实际的可用业载，可表示如下

则实际业载（APL，actualpayload）重量和剩余业载（RPL，remaining pay load）分别与可用业载存在如下关系

式中：WAPL为实际业载重量；WRPL为剩余业载重量。

1.2 重心

重心是飞机各部分重量合力的着力点，重心位置在很大程度上影响飞行员对飞机的操控和航班的燃油消耗。确定重心的力学原理是合力矩定理，即合力对作用点的力矩等于各分力对作用点的力矩之和，如图1 所示，其中产生力矩的主要重量有业载重量、燃油重量以及营运空机重量。

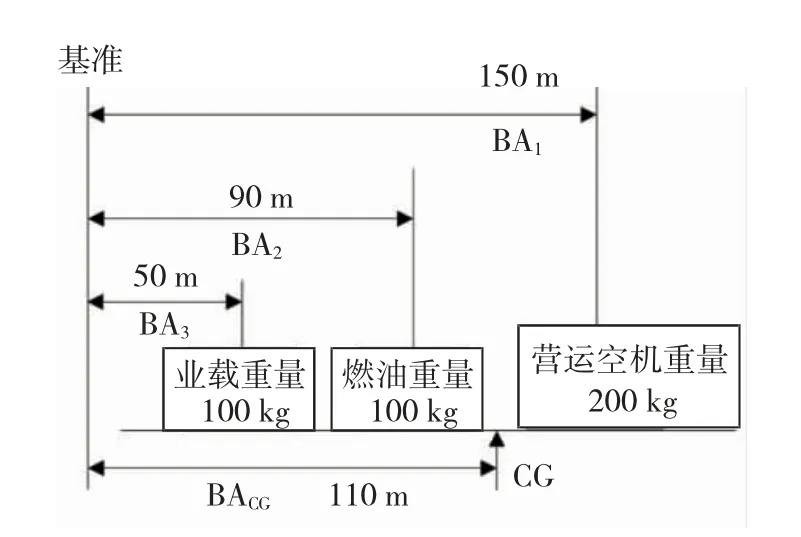
图1 合力矩定理原理Fig.1 Principle of resultant moment theorem

图1 中，假设营运空机重量为200 kg，业载重量为100 kg，燃油重量为100 kg。飞机的基准（datum）通常在其前面。平衡力臂（BA，balance arm）是基准与重心（CG，centre of gravity）之间的距离，其中LBA1、LBA2和LBA3分别为营运空机、燃油和业载的平衡力臂。由合力矩定理可知图1 中装载业载和燃油后飞机的平衡力臂LBACG为110 m。

因此LBACG的表达式如下

式中：Wi为飞机第i 个部分的重量；LBAi表示飞机第i个部分的平衡力臂。

飞机重心位置描述通常有两种方式，分别是平衡力臂与平均空气动力弦（MAC），平衡力臂描述如式（6）所示。平均空气动力弦是用平衡力臂LBACG与平均空气动力弦前缘长度的差与平均空气动力弦长度的比值表示，即

式中：LMAC为平均空气动力弦的长度；LEMAC为平均空气动力弦前缘长度。图2 为客机改装后的参数示意图。

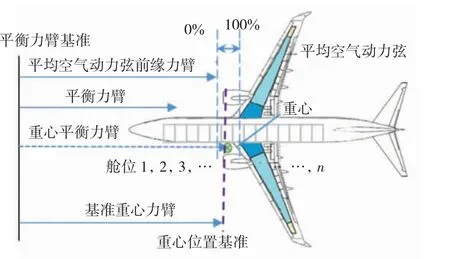
图2 飞机客舱改装后参数示意图Fig.2 Schematic diagram of aircraft cabin parameters after modification

1.3 重心包线

为了保障航行中飞机的平衡与安全，业载应被放置在货舱内合适的位置，使飞机重心正好在重心包线的范围内。飞机的重心包线是分段非线性函数，由最大起飞重量、最大着陆重量和最大无油重量等不同重量的最小重心和最大重心所组成。B757 的重心包线如图3 所示。

图3 B757 的重心包线Fig.3 CG envelope of B757

其中，纵轴表示飞机的总重量，横轴为指数，表示力矩。重心包线的应用可以避免相关风险，使航行中的飞机实现高效安全运行，且其在现实的飞机载重与平衡工作中非常重要，目前尚无法替代。

2 民用航空货运配载问题研究方向

文献[5]最早对飞机载重平衡问题研究文献进行了综述。其中提出，1985 年之前大多数配载都是由手工和计算机协助完成的。配载员的工作是制定一个可行计划，而不是一个理想的配载方案。重心的约束通常通过金字塔模式装载来解决，即依次将最重的货物分配到飞机中心位置，然后交替对飞机的前后舱进行装载。

根据文献研究方向的不同，航空货运配载有关研究文献可以分为3 类，即货物运输计划、货物装箱问题和集装器装载配平问题。

2.1 货物运输计划

货物运输计划指的是对给定的一组货物选择合适的飞机机队，按要求在指定的时间窗口内将货物分配到飞机上允许的位置，并运送到目的地。图4 是根据时间进程绘制的部分学者研究成果。

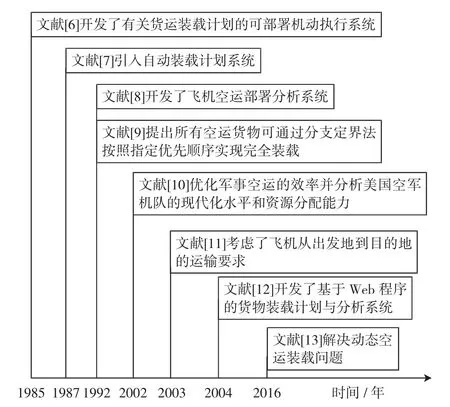
图4 货物运输计划研究成果Fig.4 Research results of cargo transportation planning

文献[6]开发了用于快速生成空运装载计划的可部署机动执行系统，该系统旨在提高飞机在空运中的利用率和响应能力。文献[7]引入自动装载计划系统，用来协助运输员生成实时装载计划，评估特定装载策略的效果并验证根据用户需求制定的装载计划是否满足所有特定约束。文献[8]开发了飞机空运部署分析系统，用来调度飞机、机组和任务资源，可以最大程度地按时交付货物并送达乘客。文献[9]针对军事航空货物运输问题，提出所有空运货物可以通过分支定界法按照指定优先顺序实现完全装载，为作战行动提供及时的货物运输计划。

文献[10]提出一种称为NRMO（NPS/RAND mobility optimizer）的优化算法，该算法可在具有时间窗口的部署环境中优化军事空运，可用来分析机队现代化水平和资源分配能力。文献[11]使用两阶段求解方法来满足飞机从出发地到目的地的运输需求，其考虑了业载、起落港口及时间窗口。文献[12]提出了一种基于Web程序的货物装载计划与分析系统（CLPA，cargo load plan and analysis system），该系统基于对历史数据的分析预测，通过数学方法优化货物装载计划，从而提高业载的载荷系数，提高航班利润。文献[13]运用禁忌搜索算法来解决动态空运装载问题，模型首先给定一组需要在预先指定时间内从始发地运输到目的地的货物，再通过动态空运装载将货物划分为飞机载荷，最后选择有效飞机，将货物分配到飞机上特定的位置。

2.2 货物装箱问题

货物装箱问题是指如何分配一组货物，并将其装到合适的集装器中。根据时间进程绘制的部分学者研究成果如图5 所示。

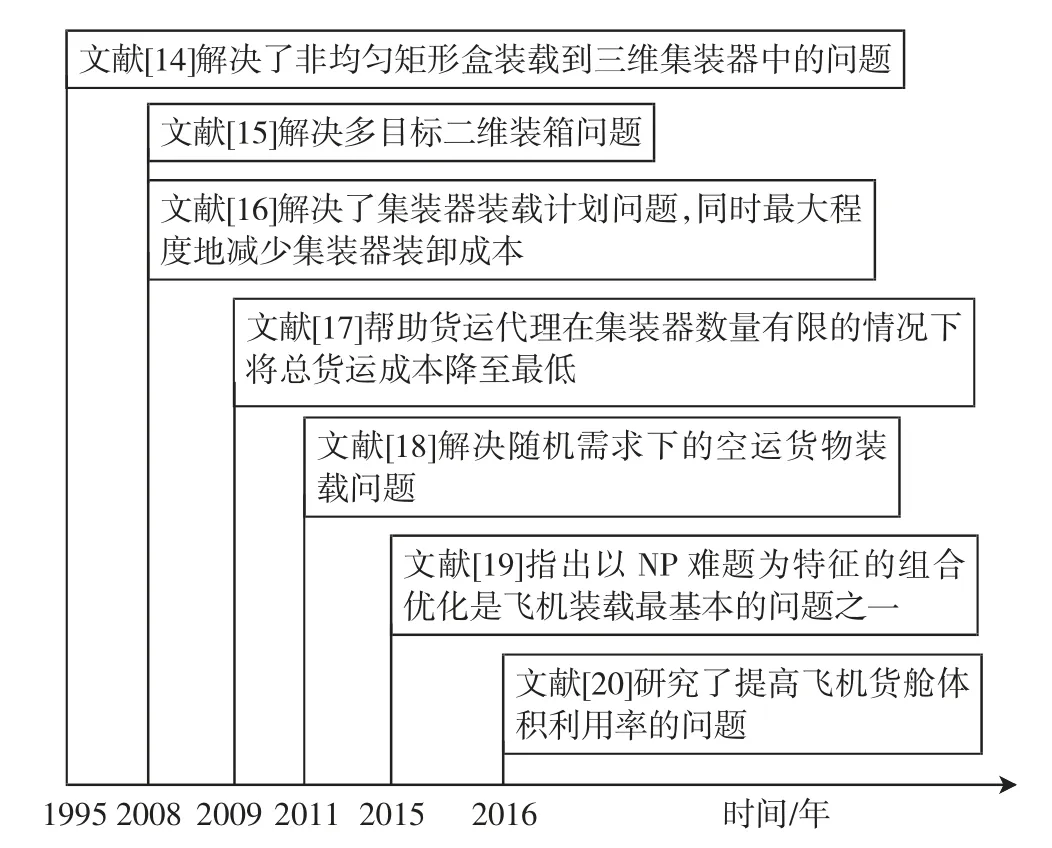
图5 航空货运装箱问题研究成果Fig.5 Research results of air cargo packing problems

文献[14]建立了将不规则物体装载到三维集装器中的0-1 混合整数线性规划模型。文献[15]使用多目标粒子群方法研究多目标二维装箱问题，目标一是最大程度地减少集装器使用的数量，目标二是最小化飞机重心与指定目标重心的偏差。文献[16]提出了一种非线性的混合整数规划模型，用于解决集装器装载计划问题，目标是最大程度地减少集装器装卸成本；其考虑了始发地和目的地需求、集装器容量、集装器数量以及每个通道集装器的装卸能力和航空器容量。文献[17]提出折中的大规模邻域搜索启发式算法，用于将货物分配到集装器内，以此帮助货运代理将总货运成本降至最低；与传统邻域搜索和混合整数规划模型相比，该算法性能更加优越且稳定。文献[18]提出一种用于解决随机需求下空运货物装载问题的方法，将情景分解和遗传算法技术相结合。文献[19]在总结航空货物运输研究文献的基础上，指出飞机装载平衡问题是航空运输中最基本的NP 难题之一，货物装入集装器后，需要考虑如何分配集装器，以满足飞机运行的各种要求，并达到某一优化效果。文献[20-23]考虑了含有不同特殊物品约束要求的三维装箱问题，进而考虑了将集装器装入飞机货舱内的问题，目标是最大程度地减少货舱内未使用的体积。

2.3 集装器装载配平问题

考虑把装好的集装器如何合理地分配到飞机不同机舱的不同位置，并在满足实际运行限制条件下，实现目标的优化，即集装器装载配平问题。该方面的研究从方法上可以分为启发式算法和（混合）整数线性规划方法。

2.3.1 启发式算法求解装载配平问题

早期对装载配平问题的学术研究相对简单，考虑实际条件较少，因此数学模型比较简单，且由于载重配平问题为典型NP 难题，因此在早期的研究中主要以简化模型和启发式智能算法为主。图6 是根据时间进程绘制的部分学者研究成果。

图6 启发式算法求解装载配平问题研究成果Fig.6 Research results of the loading balance problem solved by heuristic algorithm

文献[4]开发了一种基于启发式算法的程序来创建装载计划，以便将业载装载到B747 飞机上;目标一是在多航段的航班中尽量减少货物的额外装卸操作，目标二是获得可行的重心。该模型考虑了货舱稳定性、组合载重、货物位置、货舱容积和重量平衡约束。文献[24]分析飞机一维装载平衡问题，认为飞机装载是一个NP 难题，并考虑了装载集装器的种类、位置和装载优先次序。文献[25]将飞机装载平衡问题看作是装箱问题，把飞机当作箱子，集装器当作待装载货物，并运用了文献[24]的思想，使用遗传算法进行求解。文献[26]针对飞机一维装载平衡问题提出一种贪婪启发式算法，其目标是将给定长度和重量的箱子放入集装器中，尽可能使该区域的重心达到既定目标。文献[27]认为在飞机上的货物装箱属于二维装箱问题，考虑了纵向平衡、横向平衡、货物在地板上接触点的最大重量、货物所在地板区域内可承受的最大重量等约束。文献[28-29]提出一种多目标粒子群优化方法，将一组货物分配到最小数量的集装器中，然后将其放置到飞机特定的货舱内，模型目标是最大化总重量和已装载货物的总优先级，约束条件是当前重心与指定最优重心的偏离程度。文献[30]运用改进的蚁群算法开发了面向C919 的配载优化系统。文献[31-34]采用遗传算法求解飞机的重量与平衡问题。

随着对配载问题研究的深入，配载问题的结构越来越透彻，学者们开始逐步建立配载的数学模型。

2.3.2 （混合）整数线性规划方法

随着航空业的发展，航空运输对配载问题的要求越来越严格，形成了很多严格的操作规定，简单的数学约束模型很难满足实际生产的需求，迫切需要能够满足生产需求且能够准确描述现场操作情景的模型和方法。此外，启发式算法在处理大规模离散式多峰多约束模型时比较困难，且获得最优解花费时间较长，求解技术不能满足需求。2000 年之后，由于模型约束比较多，且随着分支定界、列分解的线性求解技术的发展，一批成熟的线性求解器相继出现，推动了载重配平问题的进一步发展，建立了相对复杂的（混合）整数线性规划模型，并通过线性求解器来解决实际问题。图7 是根据时间进程绘制的部分学者研究成果。

图7 （混合）整数线性规划方法求解装载配平问题研究成果Fig.7 Research results of the loading balance problem solved by（mixed）integer linear programming method

文献[35]提出飞机货舱货物分配的整数线性规划模型，目标是使运输货物的利润最大，但其没有考虑为飞机内特定集装器分配位置，同时包含重心的线性约束在计算公式中会产生非线性约束。文献[36]针对轻型飞机建立了一种整数线性规划模型，该模型用来解决轻型飞机遇到的剪切极限问题。文献[37]提出一种整数线性规划模型，目标为业载量最大，约束主要包含预定位置类型限制、各货舱容积限制、重量限制、多种集装器混装限制和重心限制等。文献[38]针对军用飞机建立混合整数线性规划模型，目标是最小化重心偏移量和最大化运输货物的价值，但其仅考虑了空间和重心约束，没有考虑在商业航空货运中起关键作用的约束。文献[39]建立了混合整数线性规划模型，目标是使飞机重心偏离目标值最小和所装载货物价值最大。该模型求解速度较快，然而重心约束与目标值存在一定偏差，也没有使用飞机重心包线，这导致飞机在实际工作中存在安全风险。文献[40]提出了集装器分配到装载位置的混合整数线性规划模型。该模型考虑了飞机的纵向和横向不平衡、集装器的组合装载、累积装载等约束，目标是使飞机的惯性矩和飞机结构应力以及燃油消耗最小化，但该模型无法解决集装器多于预定义位置的问题。

对于多航段飞行飞机配载问题，文献[1]和文献[41]建立了一种用于解决多航段飞行飞机配载问题的混合整数线性规划模型，目标是最小化由重心变化引起的燃油成本和中转机场重新装载集装器的操作成本之和，考虑舱位重量、组合重量、累积重量限制和货运约束。但在中间机场不允许过站集装器调整位置，失去为后一航段优化重心的机会。文献[42]建立了一种多航段货运配载问题的混合整数线性规划模型，目标是最大化装载量、最小化重心偏离量和减少中间机场额外的集装器装卸操作。模型中考虑了多种现实操作的限制条件，但位置重量、累积重量和上下舱联合重量限制被定义为统一的重量限制约束，与实际运行相差较远，且在中间机场操作中并未考虑被留在货舱集装器的位置变化。文献[43]提出了一种基于不同状态下实际重心变化的重心包线约束，并对重心进行了精确描述，进而设计了线性化策略来简化非线性的重心包线，在考虑位置、重量、平衡等约束条件下，建立了总业载最大、重心偏差最小的混合整数线性规划模型，使用商业求解器可在几秒钟内得到最优解。

2.4 整数规划模型的对比

整数规划模型已逐渐成熟，以下讨论生产实践中需要的约束问题。飞机载重配平问题的约束主要如表1 所示。

表1 载重配平问题Tab.1 Load balancing issues

表2 中详细对比了不同混合整数线性规划模型，其中相同的约束已经略去。文献[39]、文献[41]和文献[42]考虑的是集装器的数量少于可用的预定义位置数量，因此假设所有的集装器都可以装入飞机。因此，业载是不变的，只需考虑不同集装器装在什么位置，这可以归类为广义的指派问题。

表2 混合整数线性规划模型对比Tab.2 Comparison of mixed integer linear programming models

对于航空运输来说，最大装载量就是最大化经济效益。多数情况下，航空货运公司对应的航线都会存在需要紧急运送的货物，因此最大装载量有很重要的现实意义。

文献[1]和文献[38]首先从备选集装器中选择几组集装器，将其分配到飞机不同的机舱内，从而实现最大业载或运输效益，这相当于背包问题。其次，每个被选中的集装器要分配到相应的位置，使得重心偏离指定重心最小，这属于广义的指派问题，因而载重配平问题是一个组合优化问题。

文献[40]和文献[41]研究中，因集装器可以全部装上，业载不变，如果给定航班则燃油也是常数，则配载不会使飞机的重量发生变化。因此在其研究中没必要考虑重心包线问题。因为重量恒定，重心前限和后限不会随重量发生变化，只需根据当前的飞机重量确定飞机的重心前限和后限即可，如图3 所示。为了更简化模型，其采用了重心偏差约束，即重心要落在允许的重心偏差范围之内，如图8 所示，其中Xtarget表示飞机的最优重心，ε 表示飞机重心可偏离的范围。

图8 重心偏差约束Fig.8 Devitation constraint of CG

但这种脱离重心包线的方法无法在实际中应用，重心包线检查是飞机放行中非常重要的环节。

文献[1]和文献[38]以装载最大业载为目标，文献[42]以最大化装载量为目标，这使得飞机的业载和总重量会随着选择不同集装器而发生变化。由图3 可知，当重量变化时，重心范围也会发生变化。但其在重心约束方面，仍然没有采用重心包线约束，而是采用了力矩偏差。

载重配平的关键约束是重心约束，其本质是重心必须落在重心包线之内，但就当前所掌握的文献而言，还没有文献把完整的重心包线考虑进去，也没有文献对重心包线进行数学建模。而重心包线是在实际操作中必须执行的，是航班放行的条件，因而当前文献模型还无法完全应用于实际配载操作中。

重心包线是重量的函数，重量与业载相关，航班的业载取决于选择的集装器，因此重心前后限制与集装器的选择有关，而重心位置也与集装器选择有关；又因力矩（或指数）是重量与重心位置的乘积，因此重心包线约束至少是二次约束，不是线性约束。对于非线性模型，再结合其他众多约束，使得在模型求解时无法采用现有的Cplex 等通用求解器求解。这也是早期的配载模型采用启发式算法求解的原因。而近期的研究模型（表2）中，尽管模型已经与实际操作非常接近，但在关键的重心包线方面还是做了不同程度的简化。

3 配载技术的发展及应用现状

3.1 配载技术的发展

从航空发展历史来看，飞机的载重配平问题经历了3 个阶段。

（1）手工配载阶段。民航发展初期，航班配载主要通过手工舱单进行操作，人工操作和计算耗时较长，特别是大型飞机的货运配载需要的时间更长，误差也较大，为了克服误差带来的潜在威胁，很多航空公司对包线进行缩减。目前绝大多数航空公司已经不再进行完全的手工操作。

（2）计算机辅助的半手工配载阶段。计算机软件用于辅助配载，在很大程度上解决了人工手动操作时间较长的问题，当前多数航空公司和配载单位都处于该阶段。典型的代表有EXCEL 辅助重心计算，某航空公司的EXCEL 辅助配载如图9 所示，EXCEL 函数功能能够实现自动计算配载力矩、重心位置等基本参数，但是仍需要手动输入各集装器信息，如何配载仍然需要人工决策。

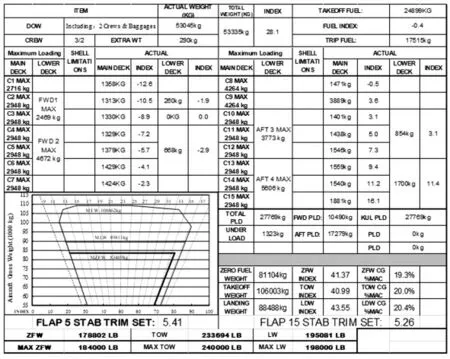
图9 EXCEL 辅助配载Fig.9 EXCEL assisted loading

近几年，窗口版配载系统在部分航空公司出现，如图10 所示，其主要功能是人机交互式配载、配载规则自动检查、配载单自动打印和发送等。但配载方案仍需要人来提供。

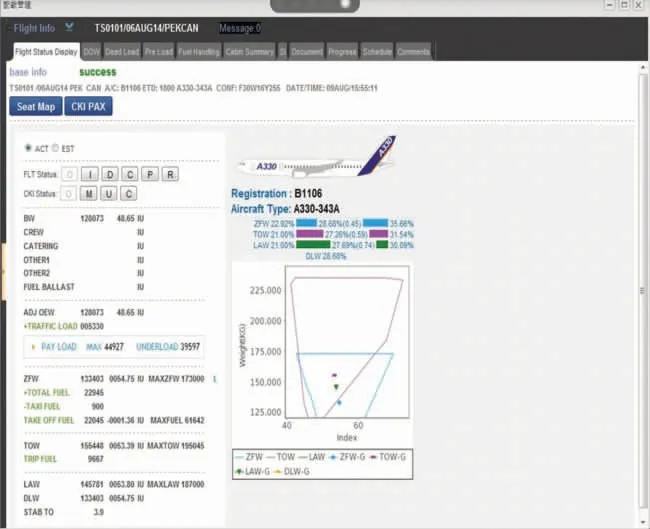
图10 交互配载系统Fig.10 Interactive loading system

（3）自动配载阶段。配载软件能够根据给定的机型、货物、旅客、集装器等情况自动给出一种或多种配载方案，供配载人员选择，并能够根据需要进行人工交互调整。当前部分公司已经进入该阶段。但自动配载依然在多集装器混装、多航段联合、业载优化、重心偏差分析、配载专家经验偏好等方面还存在欠缺。

这3 个阶段配载方法的本质是相同的，都是枚举法。手工阶段和计算机辅助的半手工阶段是通过配载员个人经验枚举出配载方案，然后按照规则进行检查，如配载方案不符合规则或与期望配载结果相差太远，则重新调整枚举方案，直到获得满意的配载方案，但耗时较长，且配载结果依赖于个人经验；目前自动配载阶段的软件方法依然属于枚举法，是把人工操作过程通过软件实现，通过软件自动产生初始配载方案，通过“冒泡”“爬山”等排序法反复调整和检查配载方案，最终获得可行的配载方案。

枚举法的优点在于符合传统配载操作思维习惯，容易接受。但其缺点也很明显，即无法遍历所有可行域，获得全局优化，最终只能找到一个可行方案，不能穷举所有配载方案。因此，该方法的本质决定了在混装、重心和业载优化、重心偏差、过站操作、公司政策偏好等智能方面优化能力不强，无法给出智能化、个性化方案。

一方面由于多数航空公司配载还没进入自动化阶段，另一方面随着计算机计算能力的不断增强，使得配载的枚举法还会继续存在一段时间。但随着航空公司的精细化发展，对各环节利益诉求逐渐增强，对配载方案的要求越来越多，该方法的弊端将会逐渐暴露，将会阻碍航空公司的精细化、智能化进程。

3.2 集中配载的应用

集中配载是以载重平衡为中心，实现集中控制其他航站载重平衡工作的一种全新运行模式。当前航空公司在配载模式上依然采用分散配载，分散配载存在货运系统与配载系统数据自动化对接的困难，而集中配载可实现数据资源共享，远程操控等。

4 对配载技术的展望

民用航空运输载重配平在未来可采用机器学习、整数规划方法、智能优化算法等人工智能技术，主要解决以下几个问题：

（1）飞机载重配平的智能化水平不高，配载员业务水平存在差异，专家经验依赖性强，多种集装器或特殊物品混装时手工操作复杂度高；

（2）重心优化少，缺少航班运行各阶段实际重心与理论重心的偏差预测，有备选集装器可供选择的条件下业载优化较少，多航段关联配载时存在中间机场额外装卸操作等一系列问题。

基于上述对配载问题的分析，对配载的未来展望如下：

（1）实现集中配载，将航空公司运营的所有航班集中在一个点进行飞机配载，便于集中培训、统一操作标准和降低不安全事件的发生率；

（2）优化航空运输中飞机的载重配平，实现配载的自动化和智能化，集中配载数据，以提高配载效率；

（3）通过专家经验、飞行中的重心变化推演和突发扰动下的重心偏离分析，建立配载效果的评价指标体系；通过AI 机器学习算法，对优秀配载案例进行特征学习；建立具有公司偏好的整数规划模型，实现具备公司特征的智能配载方案。通过计算机归纳、学习优秀员工的先进经验，可使配载方案更贴切公司运行特征需求。

5 结语

民航货运载重与平衡问题属于典型的NP 难题，需要综合考虑重心约束、载重量、体积利用率和航空公司所得利润等，建立模型需选择合适的求解方法。本文主要介绍了国内外学者对载重平衡问题的建模与求解方法，并且将其分为3 大类，即货物运输计划问题、货物装箱问题和集装器装载配平问题。根据模型的求解方法将配载问题又分为两大类，即启发式算法和（混合）整数线性规划方法。尽管目前的配载模型解决了大量问题，但还有待进一步完善。

启发式算法尽管在某些条件下可以获得满意解，但其依然是行业“枚举法”的延续，并不能很好地解决配载问题。（混合）整数线性规划方法目前的配载模型已经与实际问题非常接近，但在重心包线问题上却进行了简化，使得该方法偏离了实际操作。

因此，未来飞机载重配平问题应当进一步完善（混合）整数线性规划模型，将重心包线模型化、线性化，彻底实现载重配平问题的数学模型表述。另一方面，配载中还存在一些实际问题，如多航段关联配载、超大货物或不规则货物的配载、集装器的重心不确定性、符合各公司特殊要求和政策的个性化配载、专家经验相结合的智能化配载以及基于风险思维的航空配载运输任务方案优化与评估等问题。