单轴压缩下不同饱和度红砂岩横波特征研究
2024-03-13程锦山管华栋王观石汪永超林强
程锦山, 管华栋*, 王观石, 汪永超, 林强
(江西理工大学,a.江西省环境岩土与工程灾害控制重点实验室;b.土木与测绘工程学院,江西 赣州 341000)
0 引言
地下岩土工程长期受地下水和地表水的影响,从而导致各种灾害的发生,如:受水影响可能导致岩溶塌陷[1-2],壤盐碱化[3]、流砂、管涌[4]。超声波测试技术[5-6]属于无损检测,可以重复试验,检测快速且成本低,为此超声波测试技术在岩土工程领域被广泛用于解决岩体质量评定、岩体结构的分类及岩石参数测试[7-9]等问题。含水率会影响超声波在岩石中传播特性,基于干燥状态下声学参数与力学参数之间内在联系去研究饱和状态下两者之间关系会产生较大误差。因此,研究不同饱和状态下超声波传播特性对准确获取声学参数具有重要意义。
赵修成等[10]、黄志辉等[11]通过超声波纵波波速与岩石物理、力学参数的变化关系,建立了纵波波速与岩石物理、力学之间的内在关系。李楠等[12]研究了煤岩纵波波速受孔隙率及含水饱和度的影响,研究表明高孔隙率煤波速受饱和度影响大于低孔隙率,饱和度越高,波速受孔隙率影响越小。范翔羽等[13-14]通过研究不同层理倾角和含水率对岩样纵波波速影响,发现不同层理倾角对纵波波速影响大于含水率。张明明等[15]、张超等[16]对干燥和饱和状态下碳酸盐声学参数及衰减规律进行研究。陈旭等[17]对不同含水率红砂岩、大理岩、花岗岩进行超声波测试,结果表明3种岩样纵波波速饱和状态下比干燥状态略高,揭示纵波波速受岩石致密程度、孔隙度、密度等影响。张天军等[18]通过研究不同饱水状态下含孔试样破坏过程中超声波特征,发现波速均值与含水率表现呈负相关,破坏过程中,波速呈现出稳定-轻微降低迅速降低3个阶段。夏冬等[19]对浸水时间对饱和闪长岩和灰岩进行超声波测试,研究表明在浸水时间14 d前纵波波速下降幅度大,14~60 d下降幅度变小,浸水60 d后纵波波速变化倾向稳定。杨为民等[20]利用岩样孔隙率和饱和状态作为媒介建立纵波波速与电阻率的联系,结果表明,通过岩样实验实测数据拟合较好,验证其合理性。以上的研究主要集中在岩石纵波波速随饱和度变化关系,对于其他波形特征随饱和度变化规律研究甚少。事实上,岩石超声波横波的声学参数与饱和度也存在内在联系[21],通过研究岩石横波声学参数的变化可以为估算不同饱和状态下力学性能奠定基础,但此类相关的研究成果较少。
红砂岩是赣南地区特有岩石,遇水容易崩解、软化[22-24],因此本文以红砂岩作为研究对象,开展不同饱和度下超声波横波测试,分析红砂岩横波声学参数随饱和度的变化规律,探寻对饱和度变化最为敏感声学参数,为进一步揭示岩石软化机理奠定实验基础,并为不同饱和度下岩石超声波声学参数测试技术发展提供参考。
1 实验部分
1.1 岩样试件制作
将岩样制作成高径比为2∶1,在岩样整个高度上直径误差不得超过0.3 mm;岩样两端面的平整度误差最大不超过0.05 mm;岩样两端面垂直岩样轴线,最大偏差不超过0.25°。各个岩样的直径、弹性模量、密度、孔隙率、高度如表1所列(在实验过程中,编号H-1~H-3在饱水过程中发生劣化,故后期没对其进行讨论)。
1.2 实验装置及方案
实验过程中采用仪器:烘干箱、高精度电子天平、HS-YS301C型岩石超声波测试仪(图1)。实验按照以下流程进行:①先测量试样尺寸,将试样全部浸入在水中自然吸水48 h后含水岩样连续3次称其质量差不超过0.01 g为止,此状态定为饱和状态质量mw,并进行超声波测试;②将岩样按规范[25]要求进行烘干(岩样放置烘箱机内,温度调至105 ℃加热12 h后让其自然冷却到室温),测出其干燥质量ms,并进行超声波测试;③将红砂岩放入水中没过岩样表面浸泡进行自然饱和,期间定时(3、8、15、48 h)测量不同饱和状态下岩样的质量mi,并进行超声波测试。

图1 多频率声波测试示意Fig.1 Schematic diagram of multi frequency acoustic testing
1.3 参数计算
红砂岩含水饱和度通过式(1)计算:
式(1)中:ms为岩样的干质量;mw为岩样自然吸水饱和质量;mi为岩样浸水i小时后的质量。
横波波速测试主要采用方法有反射法和透射法,本文实验采用透射法。实验中采用HS-YS301C型岩石超声波参数测试仪,横波换能器的入射频率分别为50、100、 200 kHz,换能器与岩样之间采用锡箔纸耦合,每次测试前先用标准铝块对仪器进行标定,确保仪器发射信号稳定,测试时岩样测点固定,岩样施加应力为500 N(此应力下呈现波形图最为直观),温度为室内正常温度。横波波速的计算如下:
式(2)中:L为岩样长度;t1为岩样横波探头对接起跳点时间;t0为系统延迟时间。
声波在岩石内部传播过程中,遇到节理、空隙微裂纹等不连续介质,会产生折射、散射等现象发生,从而导致幅值等声学参数变化,进而会影响波形的变化。根据实验所测得波形数据,横波幅值衰减系数计算如下:
式(3)中:A为超声波探头对接最大电压幅值;A1为超声波在岩样透射端的最大电压值。
2 实验结果与分析
2.1 不同入射频率下红砂岩横波波速随饱和度变化规律
根据式(1)、式(2)分别计算不同入射频率下砂岩饱和度与横波波速,表2所列为多种函数回归拟合结果,从表2发现3次多项式函数的拟合决定系数在几个回归模型中最优(限于篇幅仅给出部分实验拟合结果)。由表3—表5可以看出入射50 kHz决定系数波动范围在0.857~0.972 2之间,入射频率分别为100 kHz及200 kHz,拟合决定系数分别在0.857 1~0.983 7、0.824 0~0.980 5,可见拟合效果较好,属于高度相关。故本文采用三次函数拟合曲线对横波波速随饱和度和入射频率变化关系展开讨论。
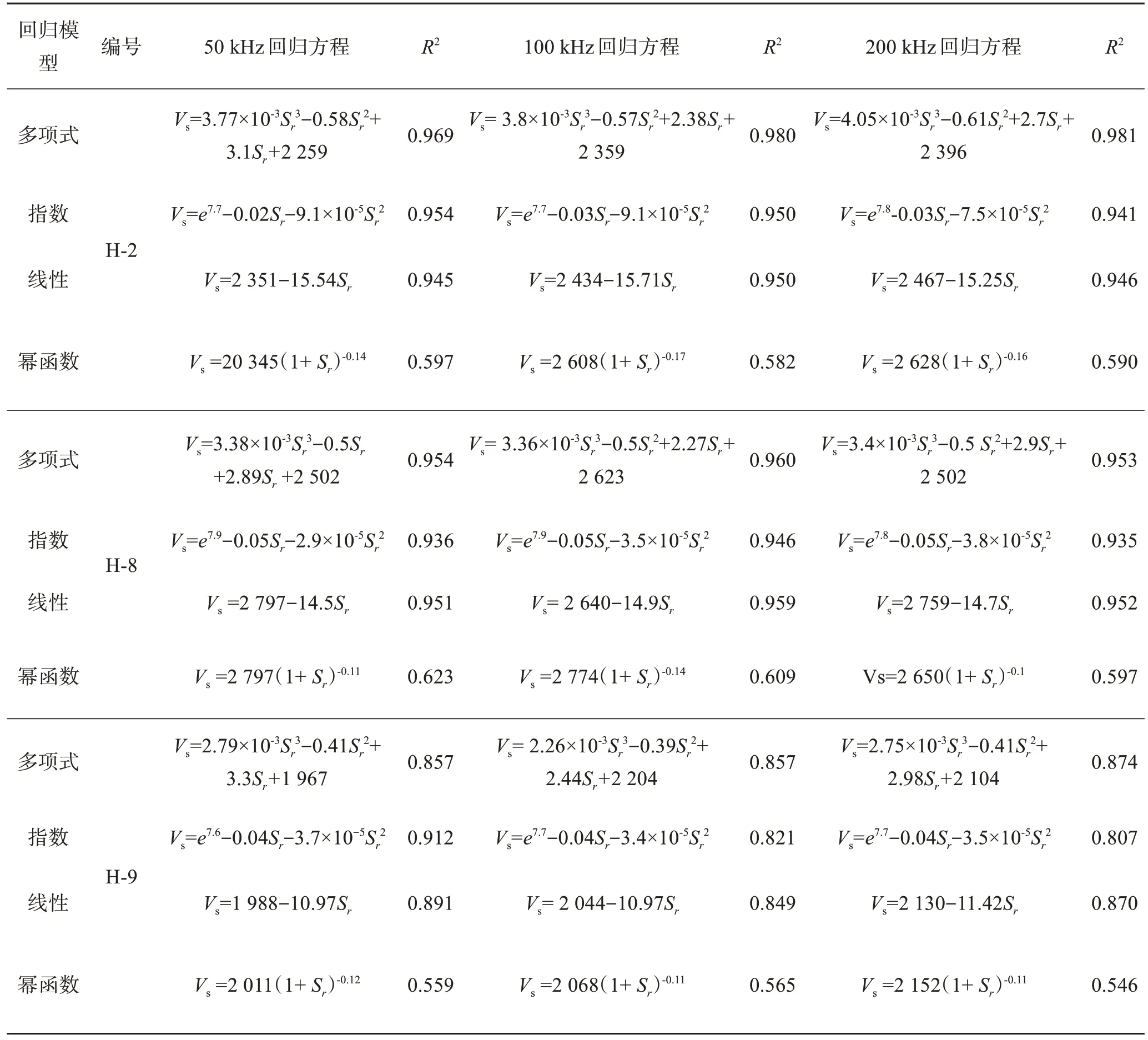
表2 横波波速与饱和度回归方程拟合结果Table 2 Fitting results of S-wave velocity and saturation regression equation
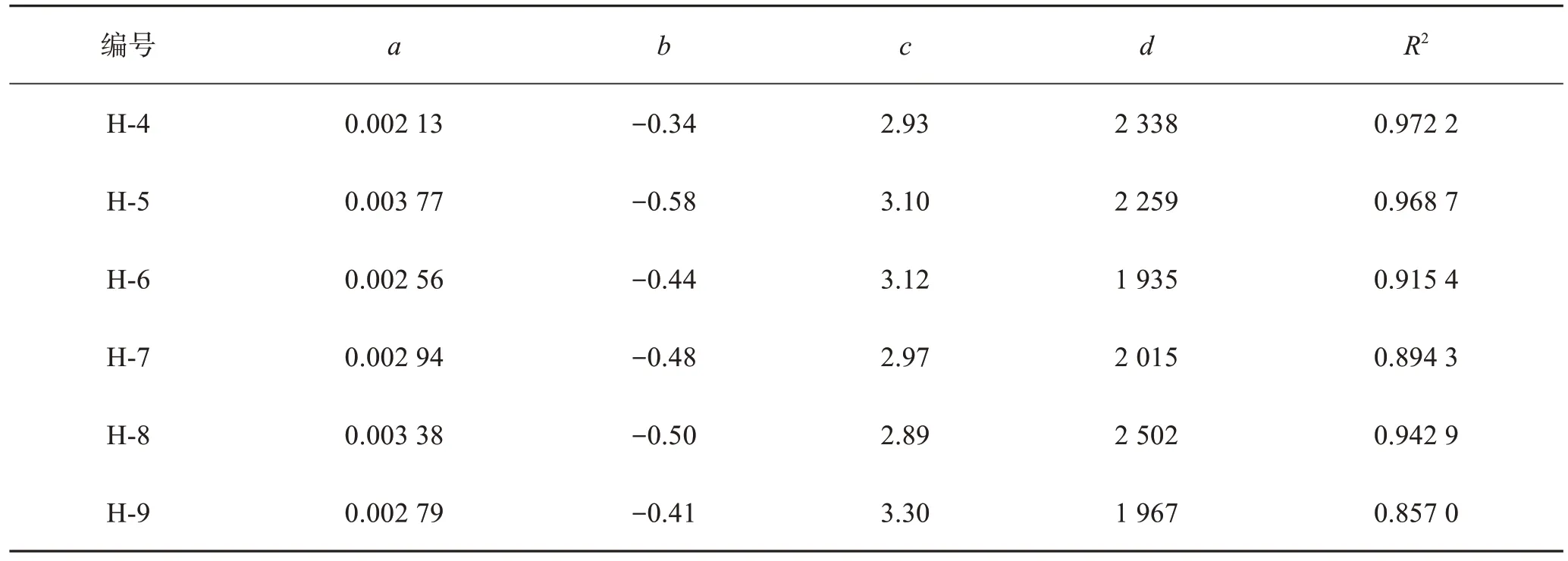
表3 入射频率50 kHz横波波速拟合参数Table 3 Fitting parameters of incident frequency 50 kHz shear wave velocity
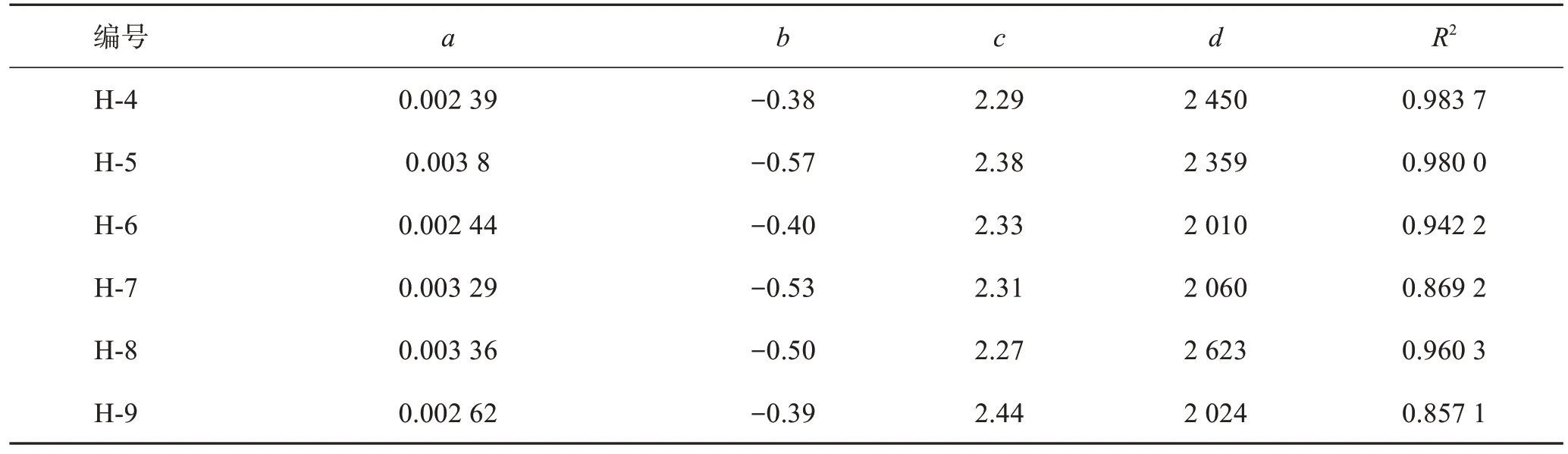
表4 入射频率100 kHz横波波速拟合参数Table 4 Fitting parameters of incident frequency 100 kHz shear wave velocity
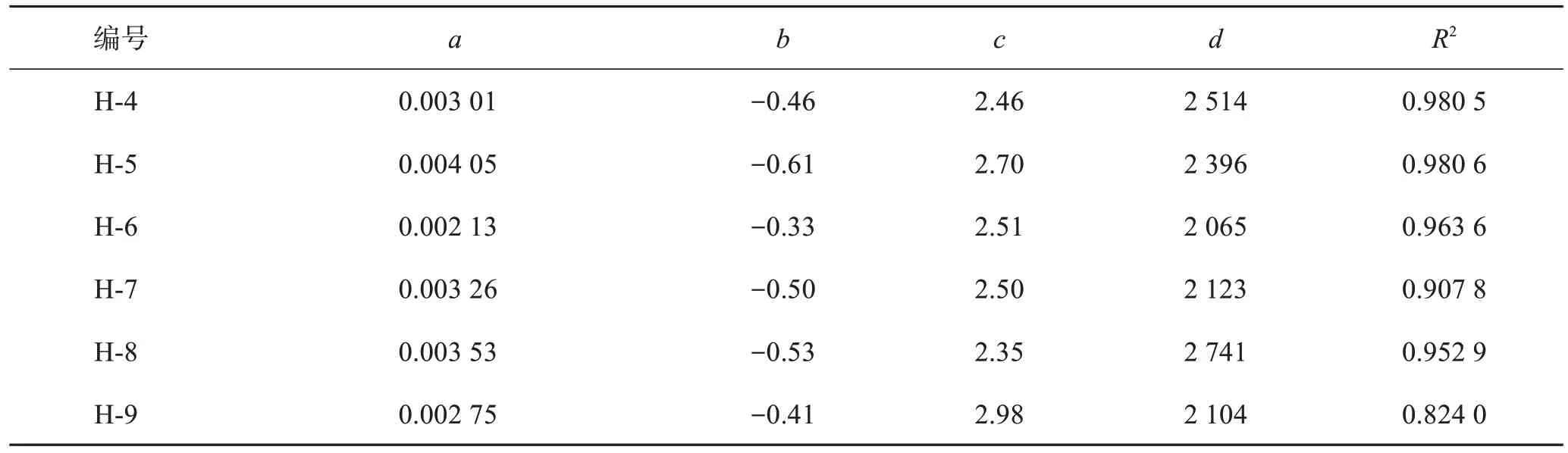
表5 入射频率200 kHz横波波速拟合参数Table 5 Fitting parameters of incident frequency 200 kHz shear wave velocity
图2所示为不同饱和度和频率对横波波速的影响(限于篇幅仅给出部分实验结果),从图2发现,不同入射频率下随饱和度的增加,岩样横波波速呈现非线性下降趋势,入射频率为50、100、 200 kHz干燥状态下均值分别为2 165、2 245、2 320 m/s,饱和状态均值分别为920、992、1 080 m/s ,对应下降了57.49%、55.80%、53.45%。随入射频率的增加,红砂岩横波波速呈非线性增大趋势,入射频率由50 kHz变化到100 kHz再到200 kHz,干燥状态波速均值分别增大3.70%和3.34%,饱和状态波速均值对应增大7.84% 和8.83%。这是由于本实验红砂岩具有崩解性,当浸水后红砂岩中含有碳酸盐会发生水解反应,使得颗粒之间伴随碳酸盐的逐渐水解,岩样内部结构发生改变,使得波的传播距离增加,导致传播过程中能量的损失。
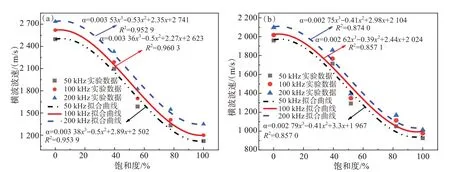
图2 不同饱和度和频率对横波波速的影响:(a) 岩样编号H-8;(b) 岩样编号H-9Fig.2 Influence of different saturations and frequency on wave velocity:(a) rock sample number H-8;(b) rock sample number H-9
分别对比横波波速与饱和度和入射频率变化的曲线斜率,红砂岩幅值衰减系数同时受入射频率和饱和度的影响,将纵横坐标进行归一化结果见表6,由表6可知3种频率下,波速随饱和度变化斜率大于波速随入射频率变化斜率,频率为100 kHz横波波速与饱和度的斜率最大。综上所述,饱和度对横波波速影响大于入射频率对横波波速的影响。

表6 不同饱和度和频率与波速变化的曲线斜率Table 6 Curve slope of different saturation and frequency versus wave velocity
2.2 不同入射频率下红砂岩幅值衰减系数随饱和度变化规律
衰减系数可以反映超声波在传播过程中距离的增加而导致波形的变化,实验所测得的波形数据代入式(3)求得各个砂岩的幅值衰减系数,且同横波波速分析方法一样,对比发现三次多项式拟合决定系数结果最好,故采用三次多项式进行拟合,拟合结果如表7—表9所示。
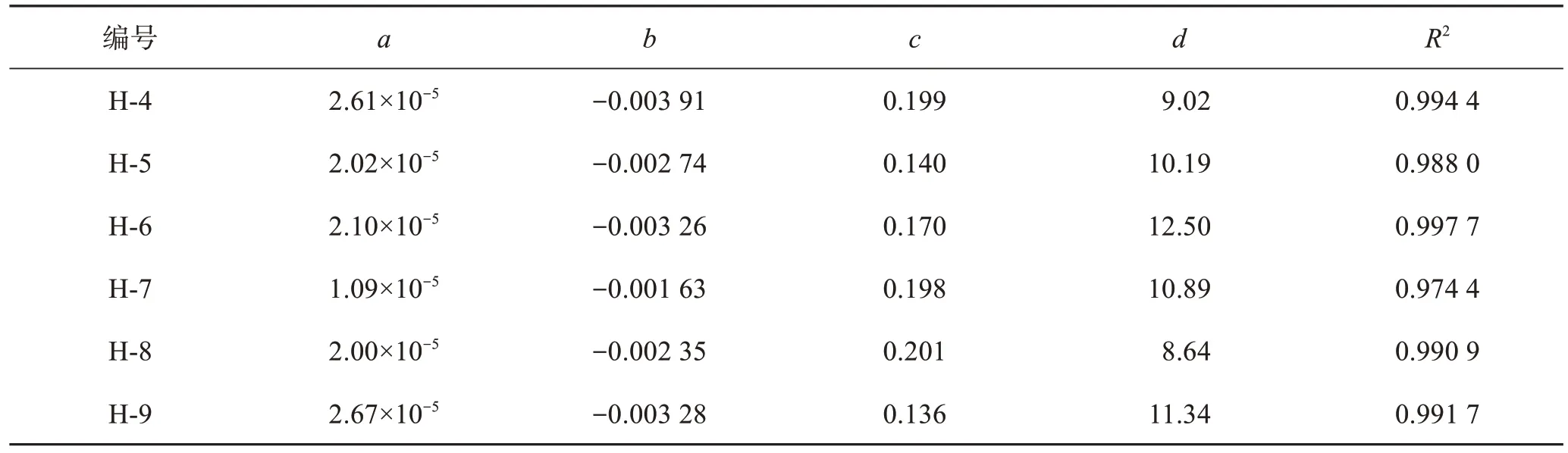
表7 入射频率50 kHz幅值衰减系数拟合曲线参数Table 7 Fitting curve parameters of amplitude attenuation coefficient of incident frequency 50 kHz

表8 入射频率100 kHz幅值衰减系数拟合曲线参数Table 8 Fitting curve parameters of amplitude attenuation coefficient of incident frequency 100 kHz

表9 入射频率200 kHz幅值衰减系数拟合曲线参数Table 9 Fitting curve parameters of amplitude attenuation coefficient of incident frequency 200 kHz
由表7—表9可以发现,入射频率为50 kHz,决定系数波动范围在0.974 4~0.997 7;入射频率为100、200 kHz,决定系数波动范围分别为0.991 2~0.999 8、0.951 1~0.990 3,属于显著相关,且入射频率为100 kHz的拟合决定系数在3种频率中最优。故后面与横波波速同样采用三次拟合函数对幅值衰减系数随饱和度和频率变化关系展开讨论。
图3所示为不同饱和度和频率对幅值衰减系数的影响(限于篇幅仅给出部分实验结果)。不同入射频率下,随着红砂岩饱和度增加,幅值衰减系数呈非线性递增趋势,干燥状态下,入射频率50、100、200 kHz,幅值衰减系数均值分别为10.71、11.56、 11.92 dB /m,饱和状态下,入射频率分别为50、100、200 kHz,幅值衰减系数均值分别为16.64、17.92、18.30 dB /m,分别增大53.50%、55.02%、53.52%。随入射频率的增加,幅值衰减系数呈非线性增加,入射频率由50 kHz变化到100 kHz再到200 kHz,干燥状态均值分别增大6.79%、3.35%;饱和状态均值分别增大 6.57%、2.52%。
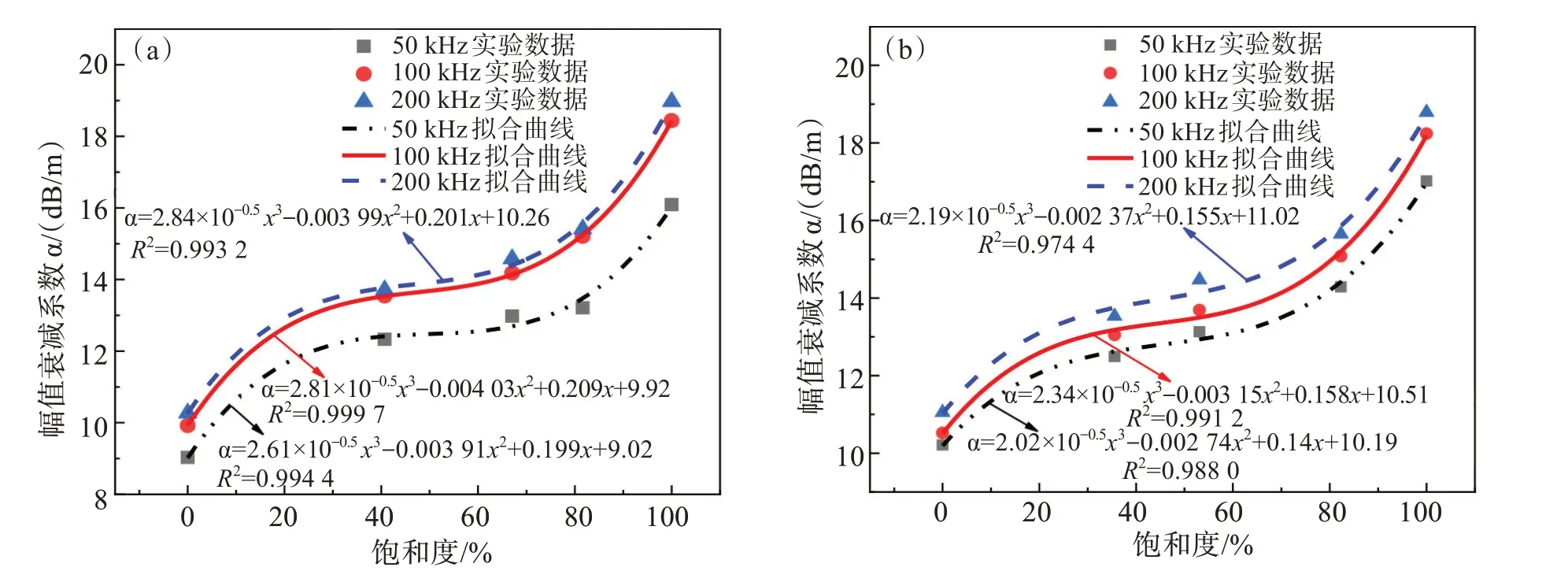
图3 不同饱和度和频率对幅值衰减系数的影响:(a) 岩样编号H-4;(b) 岩样编号H-5Fig.3 Influence of different saturations and frequencies on amplitude attenuation coefficient:(a) rock sample number H-4;(b) rock sample number H-5
基于上述分析,红砂岩幅值衰减系数同时受入射频率和饱和度的影响,将纵横坐标进行归一化处理结果如表10所列。从表10可知幅值衰减系数与饱和度的变化斜率大于入射频率。在3种入射频率下,入射频率为100 kHz幅值衰减系数与饱和度的斜率最大。由此可知,入射频率对幅值衰减系数影响小于饱和度对幅值衰减系数的影响。

表10 不同饱和度和频率与幅值衰减系数变化的曲线斜率Table 10 Curve slope of saturation and variation of frequency and amplitude attenuation coefficient
从幅值衰减系数和横波波速拟合曲线函数中可以发现:不同入射频率下幅值衰减系数拟合曲线决定系数均大于横波波速拟合曲线决定系数,故后文对幅值衰减系数拟合参数与红砂岩各物理量之间关系展开讨论。不同入射频率下幅值衰减系数拟合曲线中a、b、c和d为待定参数,为研究拟合参数对应的物理量,分别将岩样的密度、弹性模量以及孔隙率进行比对,分析拟合参数与岩样的各物理量随饱和度的变化关系。
3 幅值衰减系数拟合参数与物理量关系
由表6—表8中可以发现不同入射频率下幅值衰减系数拟合参数a和b分别与红砂岩的弹性模量、密度、孔隙率表现出均无明显的相关性,拟合参数a与各物理之间变化又正好和参数b与各物理量变化呈现出相反关系,为此将参数a除以参数b的值与红砂岩的弹性模量、密度、孔隙率之间建立关系结果如图4所示。

图4 拟合参数a/b与各物理量变化关系:(a) 弹性模量;(b) 孔隙率;(c) 密度Fig.4 Relationship between fitting parameter a/b and various physical quantities:(a) elastic modulus;(b) porosity;(c) density
从图4我们发现,入射频率50 kHz幅值衰减系数参数a除以参数b值波动范围在-0.006 44~-0.008 51之间,入射频率为100、200 kHz幅值衰减系数参数a除以参数b的值波动范围分别在-0.005 99~0.007 93和-0.005 89~-0.007 96。不同入射频率幅值衰减系数拟合参数a除以参数b值与弹性模量呈负相关,幅值衰减系数拟合参数a除以参数b值与密度及孔隙率之间表现出无明显相关。故采用参数a除以b值表征弹性模量的变化规律。
从图5可以看出,3种频率下,入射频率为50 kHz,幅值衰减系数参数c的波动范围在0.136~0.201之间,入射频率为100、200 kHz,幅值衰减系数参数c波动范围分别在0.147~0.213和0.141~0.202之间。不同入射频率幅值衰减系数拟合参数c与密度呈现出正相关,幅值衰减系数拟合参数c弹性模量和孔隙率变化呈现出无相关性。故采用幅值衰减系数拟合参数c表征密度的变化。
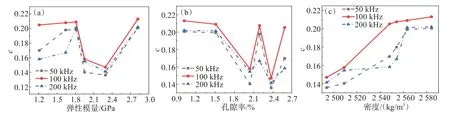
图5 拟合参数c与各物理量的变化关系:(a) 弹性模量;(b) 孔隙率;(c) 密度Fig.5 Relationship between fitting parameter c and physical quantities:(a) elastic modulus;(b) porosity;(c) density
从图6可以看出,入射频率为50 kHz,幅值衰减系数拟合参数d的波动范围在8.64~12.50之间,入射频率为100、200 kHz,幅值衰减系数拟合参数d的波动范围在9.23~13.64和9.65~13.79之间。随着红砂岩孔隙率的增加,幅值衰减系数拟合参数d呈非线性增加趋势,幅值衰减系数拟合参数d与孔隙率的变化呈正相关性;而弹性模量及密度与幅值衰减系数拟合参数d的变化规律较无相关性。因此,采用拟合参数d来表征岩样孔隙率的变化。
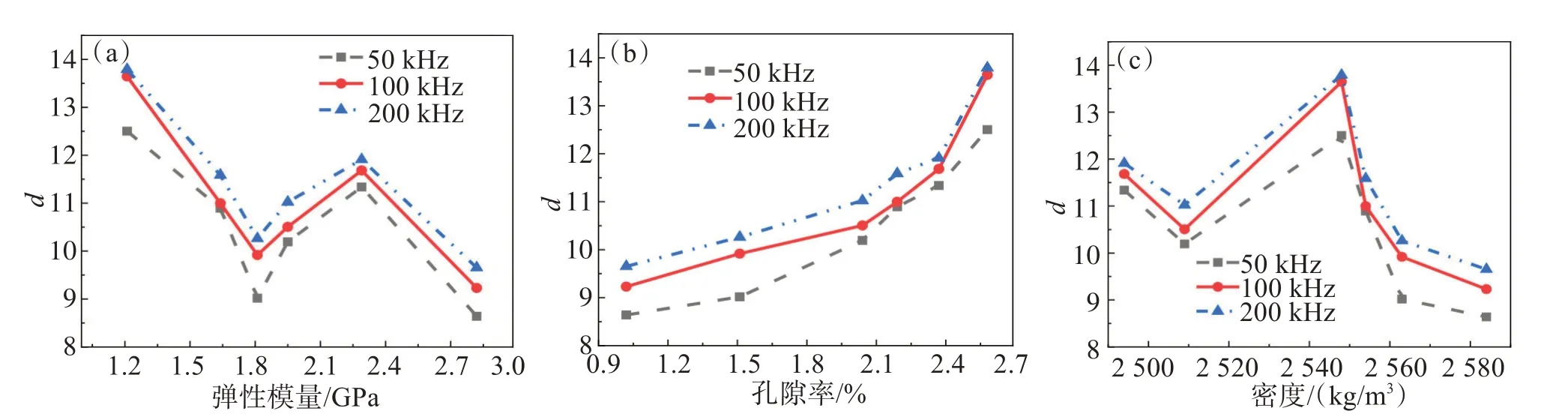
图6 拟合参数d与各物理量的变化关系:(a) 弹性模量;(b) 孔隙率;(c) 密度Fig.6 Relationship between fitting parameter d and physical quantities:(a) elastic modulus;(b) porosity;(c) density
综合考虑波速、幅值衰减系数的拟合决定系数和幅值衰减系数拟合参数与物理量的敏感性分析,幅值衰减系数与密度、弹性模量、孔隙率拟合决定系数最好且敏感性最强,故建议采用入射频率100 kHz作为红砂岩超声波横波测试优势频率。
4 结 论
通过对不同饱和度下的砂岩超声波横波传播实验,深入研究了横波波速、幅值衰减系数随频率及饱和度的变化规律,得出以下结论:
1)3种入射频率下,红砂岩横波波速都随饱和度增大呈非线性下降趋势,波速受饱和度影响大于入射频率影响。干燥至饱和状态,入射频率为50、100、200 kHz,对应波速均值下降了57.49%、55.80%和53.45%;横波波速随入射频率增大整体呈非线性增大趋势,入射频率从50 kHz变化到100 kHz再到200 kHz,干燥状态波速增大了3.70%和3.34%,饱和状态波速增大7.84%和8.83%。
2)3种入射频率下,红砂岩幅值衰减系数随饱和度增大呈非线性递增趋势,幅值衰减系数受饱和度影响大于入射频率影响。干燥至饱和状态,入射频率为50、100、200 kHz,对应幅值衰减系数均值增大了53.50%、55.02%、53.52%。幅值衰减系数随频率增大整体呈非线性增大趋势,入射频率由50 kHz变化到100 kHz再到200 kHz,干燥状态幅值衰减系数增加了6.79%和3.35%,饱和状态幅值衰减系数增大6.57%和2.52%。
3)3种入射频率下,波速和幅值衰减系数随饱和度的变化均采用三次函数拟合,波速和幅值衰减系数决定系数分别大于0.82和0.95,属于高度相关。幅值衰减系数拟合参数a除以b的值与弹性模量呈现负相关,参数a除以b的值可表征弹性模量的变化;密度与幅值衰减系数拟合参数c呈正相关,c可表征岩样密度的变化规律;孔隙率与幅值衰减系数拟合参数d呈正相关,d可表征孔隙率的变化。
4)结合敏感性和拟合曲线决定系数分析,3种频率下,入射频率100 kHz的幅值衰减系数和横波波速拟合效果最好且与饱和度敏感性最强。故后期建议采用入射频率100 kHz作为含水砂岩超声波横波测试优势频率。本文研究成果可为不同饱和状态下岩石超声波测试技术在岩土工程中的发展提供参考。
