基于谱元法的Rayleigh波频散特征计算与模态叠加耦合机理研究

杨 博,张 萌,夏江海,龙友明,吴 忧

(1. 重庆交通大学 土木工程学院, 重庆 400074; 2. 浙江大学 地球科学学院, 浙江 杭州 310027; 3. 重庆交通大学 交通土建工程材料国家地方联合工程实验室, 重庆 400074)

0 引言

成层结构中Rayleigh波(R波)频散曲线的正演计算是应用R波进行工程勘探的基本前提[1-2],代表性的有Thomson-Haskell法[3-4]、Schwab-Knopoff法[5]、δ矩阵法[6]和Abo-Zena法[7]等。在这些基础上,CHEN[8]通过定义反射与透射波传递系数,建立了基于广义反射-透射系数的R波频散曲线正演算法。袁腊梅等[9]通过无量纲化处理,进一步提高了广义反射-透射系数法的计算效率和稳定性。凡友华等[10-11]通过采用3个五阶矩阵的乘积作为传递矩阵,建立了快速矢量传递算法,同时探讨了R波频散方程高频近似分解和多模式激发数目。对于“上软下硬”的规则成层结构,大量研究表明:R波中的基阶模态能量占主导地位,此时R波频散特征就是其基阶频散曲线[12],而对于“上硬下软”、或含“硬夹层”和含“软夹层”的非规则复杂成层结构,R波频散方程变为复数方程[13],相应频散特征则是多阶模态在特定频带共同作用的结果。对此,张碧星等[14]通过构建不同激振源下R波多模态相应的位移计算方法,以此解译非规则复杂成层结构中R波频散曲线出现的“之”字形回折现象。杨天春等[15]通过对比规则成层结构与含“硬夹层”和含“软夹层”中R波谱比特征,建议实际勘探过程中须考虑R波高阶模态的影响。由此可见,探索复杂成层结构中R波多阶模态叠加耦合机理对其应用于工程勘探技术精细化提升具有重要理论意义。

谱元法(spectral element method, SEM)是一种可用于分析结构振动响应的半解析方法[16-17]。其基于波动方程,通过积分变换推导应力与位移各分量在频域-波数域的解析式,在此基础上,结合有限元思想建立结构各单元的动力刚度矩阵[18],按边界条件组装总体刚度矩阵从而计算结构的动力响应[19],具有计算精度高和速度快等优点。颜可珍等[20]基于SEM计算了半无限土基和双层土基中R波基阶与一阶模态的频散曲线。为此,本研究通过理论分析和对比计算,基于SEM建立R波可考虑高阶模态频散曲线的计算方法。同时,结合冲击振源特点,通过SEM计算R波多阶模态频散曲线的位移响应,进一步揭示复杂成层结构中R波多阶模态之间的叠加耦合频散特征。

1 基于SEM的R波频散方程

1.1 模型定义

本研究以轴对称条件下的弹性层状半无限结构作为研究对象,其每层结构介质视为均匀、各向同性的弹性体,各层沿水平方向无限且分界面相互平行,层间位移与应力完全连续,最下一层为厚度无限的弹性半无限体,如图1(a)所示。其中,r为水平径向;z为深度方向;θ为切向;E为介质的弹性模量;υ为泊松比;ρ为介质的密度;h为层厚度;N为总层数; 所有符号的下标数字及m为层序号,取1～N。

图1 构造及单元模型Fig.1 Configuration and element models

对于图1(a)中1～N-1层有限厚层结构,可视为双节点单元,如图1(b)所示,考虑有限厚度底部界面反射波的影响,其单元刚度矩阵S2-node可写为[21]

(1)

式中:μ为剪切模量;l、g和K为

(2)

式中:ω为角频率;k为圆波数;VP和VS为介质的横波速度和纵波速度。其中,VP和VS与E、ρ及υ的关系为

(3)

对于图1(a)中第N层半无限体,可视为单节点单元,如图1(c)所示,由于无限深处不存在反射波,其单元刚度矩阵S1-node可以表示为

(4)

1.2 刚度矩阵的组装

相邻m层与m+1层单元在分界面zm上节点力与位移完全连续的可表达为

(5)

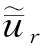
根据式(5),则完全连续相邻2个双节点单元的S2-node组装方式为

(6)

同理,第N层半无限体单节点单元S1-node与第N-1层双节点单元的S2-node组装方式为

(7)

1.3 频散方程的构建

根据式(6)和式(7),按层间接触状态拼装N层介质结构的总体刚度矩阵Sglobal,则所有节点位移与节点力的关系可表达为

(8)

det(Sglobal)=0

(9)

同时,令Sglobal中的圆波数k表示为

(10)

式中:VR为R波的相速度;f为自然频率。

将式(10)代入式(9)即得到基于SEM的R波理论频散方程。这样在式(9)中只要输入各层的弹性模量E、密度泊松比ρ、泊松比υ和厚度h,就可以得到VR随f变化的R波理论频散曲线。

2 频散曲线对比计算

为了研究SEM计算R波频散曲线的可靠性,以文献[20,22]中的弹性半无限体和“上软下硬”2种规则土层为计算模型,参数如表1中1号和2号模型。其中,第八列为第五至第七列按式(3)计算得到的相应土层材料的VS。

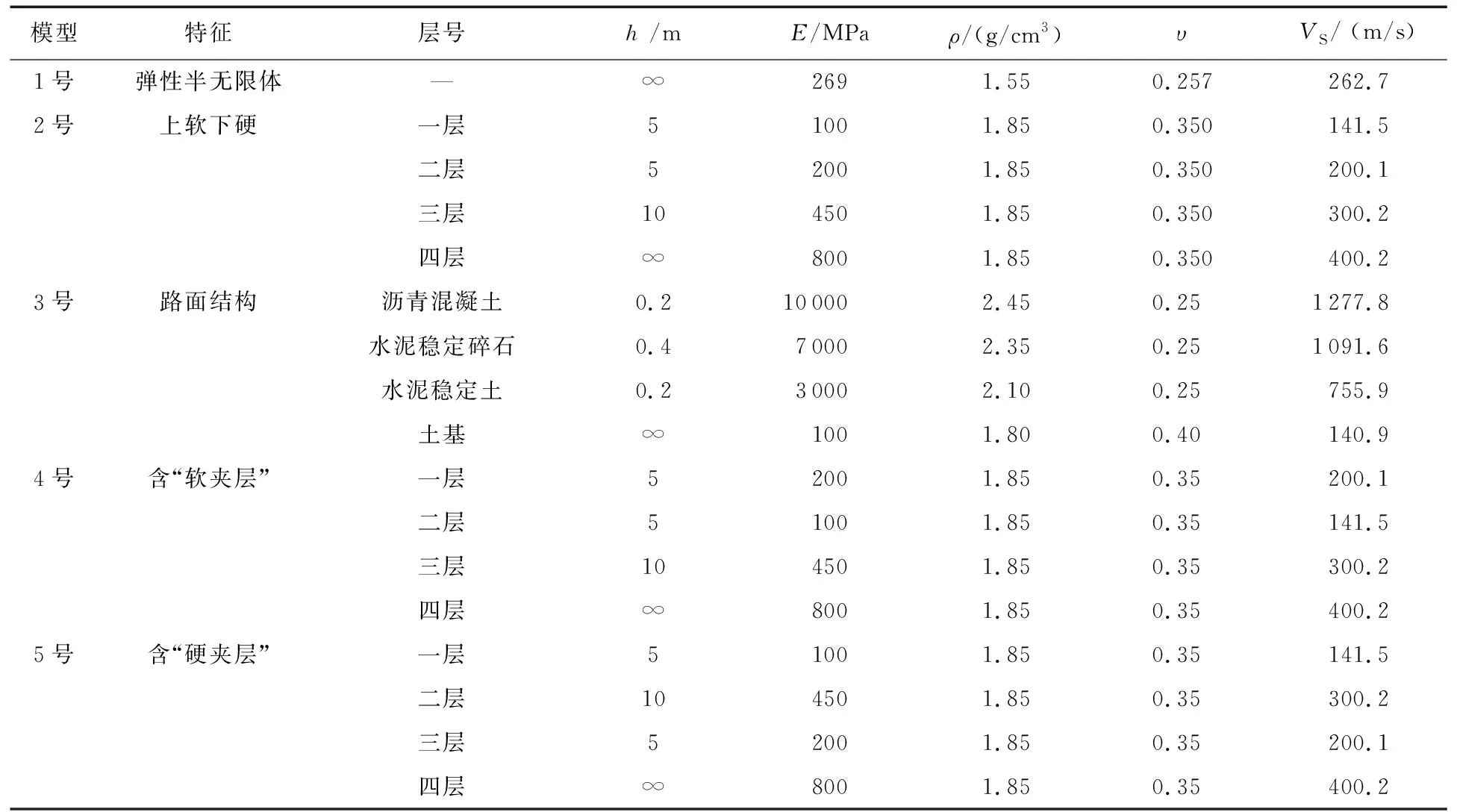
表1 成层模型的力学参数Table 1 Mechanic parameters of regular layered soil models

据此,将1号和2号模型相应参数代入基于SEM的R波频散方程式(9)中,利用二分法求根计算相应的R波理论频散曲线并与快速矢量传递法相应结果进行对比,如图2所示。

由图2(a)可知:对于1号模型半无限体而言,R波不会发生频散现象,SEM计算得到的VR在各个频率上都为241.9 m/s,与按解析式(11)计算的VR等于242.0 m/s之间的相对误差为0.03%;对于2号模型“上软下硬”的规则地层,SEM计算各阶模态的VR结果如图2(b)所示。除基阶外,其余一至七阶模态的VR均存在截止频率,计算结果与快速矢量传递法相应的结果高度吻合,相对误差均在0.05%以下,具有很高的计算精度,如式(11)所示:

(11)

3 模态叠加耦合机理分析

对于“上硬下软”、含“软夹层”和含“硬夹层”这三类复杂成层结构,具体参数[22]采用表1中的3号、4号、5号模型。其中,“上硬下软”结构以工程中常见的路面结构[24]为例,通过速度-应力有限差分方法[25]模拟竖向冲击点源作用下60道不同径向距离r对应的竖向振动记录。其中,激励采用Ricker子波,其归一化的振幅S(f)如式(12)所示,在模拟过程中为了使高频带能够获得较完整的频散信息,则最小波长λmin不得超过各模型表层h,同时为了保证在最大频率fmax处激励振幅S(f)衰减不小于0.01即-40 dB,则fm须满足式(13)。据此,结合表1中的3号、4号、5号模型具体参数,本研究将模型3号的fm取为2600 Hz[24],4号和5号模型的fm取为20 Hz,结果如图3所示。在此基础上运用相位移法[26]提取相应R波频散能量团与SEM计算的各阶频散曲线对比,以模型3号为例,结果如图4(a)所示,此时R波频散特征能量团不再以单一模态的频散曲线表征,而是多阶模态叠加耦合共同作用的结果。为了确定叠加耦合后的频散特征,以往研究根据R波为沿表面传播能量为主的一种波导,按式(14)计算各阶模态频散曲线对应的频域位移[15],以各频率表面位移能量占优模态的VR作为R波各模态叠加耦合后的频散特征,表达式为

图3 速度-应力有限差分模拟结果Fig.3 Simulation results of speed-stress finite difference method

(12)

(13)

式中:fm为Ricker子波主频;VS1为表层横波大小。

(14)

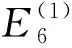
然而,式(14)是一个将R波响应当成平面波处理的积分渐进式,其求解过程中须考虑各阶模态VR所对应的极点和相应留数,因此十分复杂,且只有当r取较大时才有较好的精度。为此,本研究另从表面振动位移能量分解的角度出发,通过分析R波各模态VR对表面振动能量的贡献,建立一种确定复杂成层结构中R波多模态叠加耦合机理的半解析新方法。首先定义轴对称坐标下一个表面作用半径为a的竖向冲击荷载p(t,r)作为激励,具体表达为

(15)

式中:Q为竖向力大小;δ(t)为狄拉克脉冲函数。

相应p(t,r)的Fourier与0阶Hankel积分变换式为

(16)

当a趋于0,则激励为集中力,通过取极限和L’Hopital’s法则进一步可表达为

(17)

(18)

式中 |Uz|为各阶模态VR对表面位移即能量的贡献。

按式(18)求解各阶模态VR对应的|Uz|,归一化后得到各阶模态频散曲线对表面竖向位移贡献大小,如图4(b)所示。据此,以各频率对应表面竖向位移贡献最大相应模态的VR作为该结构中R波多阶模态叠加耦合的结果,如图4(a)中黑圈符号所示。结果表明,按此方法确定叠加耦合后的频散特征与波场数值仿真的能量团幅值能非常好地吻合在一起,不难看出基于SEM通过计算|Uz|以此确定R波多阶模态叠加耦合后的频散特征,不仅计算结果合理,与式(14)相比,形式较为简单且物理意义明确。

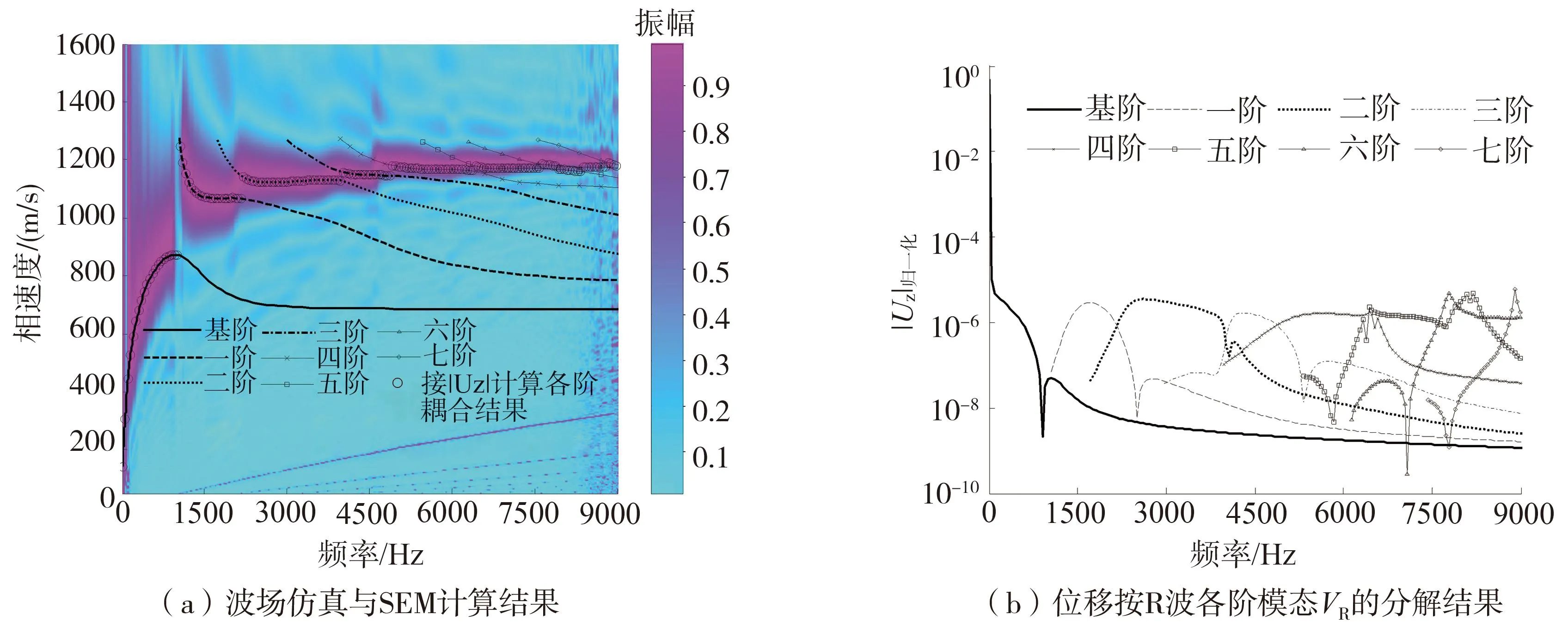
图4 3号路面结构模型中的R波频散特征Fig.4 Dispersion characteristics of Rayleigh wave in No.3 pavement structure model

同理,将4号含“软夹层”和5号含“硬夹层”结构模型按式(18)计算R波各阶模态|Uz|,并以此确定各阶模态叠加耦合后的频散特征,如图5所示,结果表明:路面结构和含“软夹层”成层结构中R波各阶模态对应的|Uz|在f较小的低频带以基阶模态绝对占优,相应频散特征以基阶模态的相速度VR表征,随着频率f增大,高频带的R波频散特征将取决于高阶模态对应的相速度VR;而含“硬夹层”成层结构中R波各阶模态对位移的贡献在高频带和低频带均以R波基阶模态为主,相应频散特征以基阶模态的VR表征,但在8～10 Hz范围的位移以一阶模态贡献为主,相应频散特征以一阶模态的VR表征。同时,图6结果表明,基于SEM确定叠加耦合后的频散特征与速度-应力有限差分方法仿真能量幅值对应的频散特征之间具有较好的一致性,平均相对误差在2.57%以下。并且,从以上结果不难看出三类复杂成层结构的R波多阶模态叠加耦合后的频散特征在高频带均收敛并接近于表面层结构的VS。因此,在计算过程中,仅需考虑基阶直至高频带VR收敛于表层结构VS的高阶模态即可。

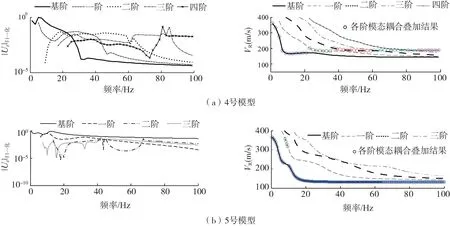
图5 含“软夹层”和含“硬夹层”成层结构中R波各阶模态叠加结果Fig.5 Modal superposition results of Rayleigh wave in soft-interlayer and hard-interlayer soil layered structures

图6 基于SEM计算结果与有限差分仿真比对Fig.6 Comparison of results calculated by SEM with finite difference numerical simulation

将图4～图6中叠加后的频散特征曲线通过半波长理论转换为VR与探深的关系,如图7所示。结果显示,3号、4号、5号模型复杂成层结构模型沿深度的频散特征均会出现“之”字形回折现象,这些可为利用R波频散特征的拐点进行结构分层提供理论参考。

图7 基于SEM叠加频散曲线沿深度特征Fig.7 Depth characteristics of stacked dispersion curve based on SEM

4 结论

本研究基于SEM建立了一种R波的频散曲线计算方法,并揭示了复杂成层结构中R波多阶模态之间的叠加耦合机理,主要结论如下:

1)本研究视轴对称条件下层状半无限结构中的有限厚度层为双节点单元,半无限体视为单节点单元,以此构建各层结构的单元刚度矩阵,并结合层间接触边界条件,建立了基于SEM的R波理论频散方程。

2)针对弹性半无限体和“上软下硬”规则成层结构,通过SEM计算R波多阶频散曲线和快速矢量传递解析算法对比发现所有结果与解析法计算相应结果之间的相对误差在0.05%以下,具有较高的精度。

3)针对“上硬下软”的路面结构、含“软夹层”和含“硬夹层”的复杂成层结构,通过SEM求解各阶模态VR对竖向位移的贡献值,建立了一种确定R波各模态耦合叠加耦合频散特征的新方法,并通过速度-应力有限差分数值仿真计算予以验证。

4)基于SEM计算叠加耦合后的频散特征曲线,通过半波长理论转换为VR与探深的关系发现,“上硬下软”的路面结构、含“软夹层”和含“硬夹层”的复杂成层结构沿深度的频散特征均会出现“之”字形回折现象,可为利用R波频散特征的拐点进行结构分层分析提供参考。