TC11钛合金动态回复与动态再结晶高温本构模型研究
2024-03-13朱宁远陈秋明陈世豪左寿彬
朱宁远, 陈秋明, 陈世豪, 左寿彬
(江西理工大学机电工程学院,江西 赣州 341000)
TC11钛合金是一种典型的α+β两相钛合金,具有比强度高、中高温性能好和耐腐蚀等特点,广泛应用于制备航空发动机压气机盘、叶片和鼓筒等零件及飞机结构组件[1]。TC11钛合金在常温下变形抗力大、塑性成形性能差,是典型的难变形材料,因此,通常采用热加工工艺制备零部件。但是,TC11钛合金在热加工过程中成形温度窗口窄,变形抗力及组织性能对温度和应变速率敏感[2]。为制定合理的工艺,充分发掘TC11钛合金的成形性能,并使所制备的零部件满足服役的性能需求,需要充分掌握TC11钛合金高温流变行为和微观组织演变规律。
基于材料力学性能试验,在分析应力应变关系、微观组织演变规律等的基础上构建本构模型,是目前研究材料流变行为的有效方法。通常,本构模型可分为统计学模型、唯象本构模型和物理本构模型。统计学模型是指通过数理统计的方法描述钛合金在不同高温下的热变形行为。已有研究者采用支持向量机与人工神经网络建立了材料的本构模型,并通过蜂群、蚁群和粒子群等算法对相关参数进行优化,取得了较好的预测结果,但该类模型的研究过于依赖回归分析等数学方法,缺乏明确的物理意义[3]。唯象本构模型能反映变形过程中的应变硬化效应、应变率强化效应和温度软化效应,主要包括基于Arrhenius双曲正弦模型[4-6]、J-C模型[7-8]和KHL模型[9],其适应性受限于热力参数取值范围。物理本构模型是指从热力学和动力学角度分析,揭示成形过程中塑性变形机制或微观组织演变机制的模型[10-11]。例如,描述位错密度的K-M模型、以位错热激活机制为基础的Z-A(Zerilli-Armstrong)模型[12]和MTS(Mechanical Threshold Stress)模型[13]等。该类本构模型能反映热变形过程的微观机理,物理意义明确,但是需建立在充分掌握变形微观组织演变机理的基础之上。
本文针对TC11钛合金中α相层错能较低而β相层错能较高的特点[14],基于对应力应变曲线与微观组织演变的分析,确定动态回复与动态再结晶的发生条件。将材料加工硬化与动态回复阶段的位错密度模型及再结晶分数模型相结合,构建了能够描述TC11钛合金动态回复与动态再结晶的高预测精度物理本构模型,为揭示TC11钛合金高温流变行为和微观组织演变规律提供了一种可靠的方法。
1 材料力学性能试验
本文利用Gleeble-1500热力模拟试验机对TC11钛合金进行圆柱单轴压缩试验,所用TC11钛合金化学成分如表1所列,其初始组织金相照片如图1所示。该组织是一种典型两相钛合金组织,主要显现为无规则排列较亮的块状、片状初生α相与较暗的β相不均匀混合的显微组织特征。

图1 钛合金初始组织Fig.1 Original microstructure of titanium alloy
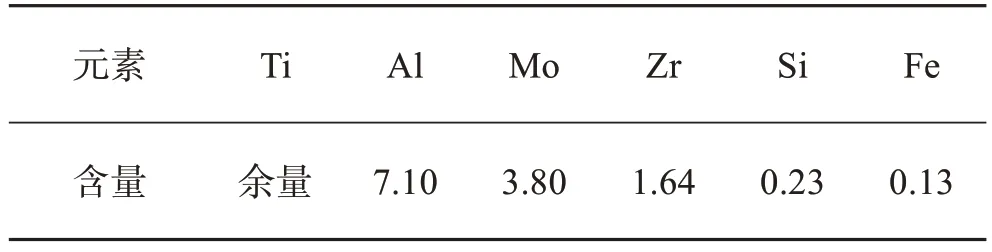
表1 TC11钛合金主要化学成分Table 1 Main chemical composition of TC11 titanium alloy单位:%(质量分数)
采用等温恒应变速率压缩变形,为确定合适的热变形温度范围,采用高温金相法与计算法测定其α+β→β相变温度为(1 015 ± 5)℃,据此设计试验变形温度分别为900、950、1 000、1 050 ℃,应变速率分别为0.1、1、10 s-1。试样采用线切割加工成ϕ8 mm× 12 mm的圆柱试样,为减小摩擦影响,打磨试样表面至光滑,并在试样上下表面添加石墨薄片,以10 ℃/s的升温速度加热至试验温度后保温5 min进行压缩试验,以克服钛合金热导率低的问题,保证试样受热均匀,当压下量达到原试样高度的60%(即真应变为0.916)时,立即水淬,以固定其微观组织,便于后续观测。为保证试验数据的准确性,每组参数条件下进行3次试验。取真应变小于0.8的数据进行研究,将数据进行去噪、光滑处理后再进行拟合,得到TC11钛合金高温热变形条件下的真应力-真应变曲线,如图2所示。

图2 不同温度和应变速率条件下的应力-应变曲线:(a)ε̇=0.1 s-1;(b)ε̇=1 s-1;(c)ε̇=10 s-1Fig.2 Stress-strain curve under different temperatures and strain rates:(a)ε̇=0.1 s-1;(b)ε̇=1 s-1;(c)ε̇=10 s-1
由图2可知,TC11钛合金高温压缩变形过程中,应力先随着应变增加而增大,直至峰值,该阶段主要表现为加工硬化;随着应变增加,应力有不同程度的下降,即发生软化;随着应变继续增加,材料的硬化效应和软化效应达到了相对平衡,应力趋于稳定,材料进入稳态变形阶段。对比图2中各曲线峰值与分布可知,TC11钛合金的流动应力对应变速率和温度敏感,应力随应变速率增加而急剧增大;应力随温度升高而降低,并且伴随温度升高,应力降低的幅度逐渐减小。另外,温度和应变速率的变化对峰值后的软化行为影响较大;随着温度升高和应变速率增加,软化程度增大,应力-应变曲线呈现动态再结晶特性;而在高温、低应变速率条件下,应力-应变曲线呈现动态回复特性。
2 TC11钛合金热压条件下的微观组织
TC11钛合金在不同热变形条件下的金相组织如图3所示,与原始状态下的组织(图1)相比,热压缩后的组织晶粒出现了明显的变形,等轴组织明显减少,初始等轴组织开始逐渐破碎,并沿材料流动和晶界方向变形。在应变速率为0.1 s-1时,动态再结晶晶粒主要在晶界周围呈链状分布,如图3(a)所示。在950 ℃时,低应变速率(0.1、1 s-1)与高应变速率(10 s-1)的组织相比,再结晶晶粒较大,等轴组织比较完整。当应变速率达到10 s-1时,晶粒尺寸较小,再结晶组织与等轴组织混合在一起。这主要是因为随着应变速率增加,相同变形量的试样所需要的变形时间缩短,变形积累的大量位错导致位错密度升高,当位错密度增加至临界值以上时,开始发生再结晶现象的形核与再结晶晶粒长大[15];另一方面,再结晶现象的发生又消解了位错的累计,使位错密度下降,而变形时间的减少使再结晶晶粒无法长大,因此在高应变速率下再结晶区域的组织更加细小均匀[16-18]。

图3 不同温度和应变速率下热压至ε = 0.916时的微观组织:(a) T=950 ℃,ε̇=0.1 s-1;(b) T=1 050 ℃,ε̇=0.1 s-1;(c) T=950 ℃,ε̇=1 s-1;(d) T=1 050℃,ε̇=1 s-1;(e) T=950 ℃,ε̇=10 s-1;(f) T=1 050 ℃,ε̇=10 s-1Fig.3 Microstructure at different temperatures and strain rates when hot pressing to ε = 0.916:(a) T=950 ℃,ε̇=0.1 s-1;(b) T=1 050 ℃,ε̇=0.1 s-1;(c) T=950 ℃,ε̇=1 s-1;(d) T=1 050℃,ε̇=1 s-1;(e) T=950 ℃,ε̇=10 s-1;(f) T=1 050 ℃,ε̇=10 s-1
温度在1 050 ℃时,所有应变速率下的组织均出现了明显晶界。在应变速率为0.1 s-1时,试样的晶界周围出现了明显的再结晶现象。当应变速率为1 s-1时,试样晶界周围的再结晶晶粒减少,晶界内出现了大量再结晶晶粒,并存在未发生再结晶的晶粒。该现象可能是由于在1 050 ℃条件下,钛合金发生了部分相变[19],组织中β相含量增加,并与α相不均匀混合,而α相与β相的再结晶条件和现象不同,应变速率的升高又导致变形时间减少,多种因素导致各个晶界内部的组织再结晶程度有较大差异。当应变速率为10 s-1时,可能是由于材料内部发生相变,试样的再结晶现象并不明显[20]。
由此可见,合理选择热变形工艺参数可以达到调控TC11钛合金组织、激活材料动态再结晶的目的,本研究通过建立位错密度模型与动态再结晶分数模型,定量描述微观组织演变过程对热力性能参数的响应,研究TC11钛合金热变形规律。
3 TC11动态回复与动态再结晶模型的建立
图4(a)所示为典型的合金材料动态回复与动态再结晶的真应力-真应变曲线,根据真应力-真应变曲线可以求出其加工硬化率θ(θ=dσ/dε),其硬化率-应力曲线如图4(b)所示。当材料加工硬化率θ=0时,其两点应力值分别对应材料只发生动态回复的饱和流动应力值σss与同时发生动态回复与动态再结晶的饱和流动应力值σdrxss,因此,σss-σdrxss即为动态再结晶导致的应力减小值[21]。令σdrv为由动态回复和加工硬化作用下导致的应力变化值;σdrx为动态再结晶软化作用下导致的应力变化值。
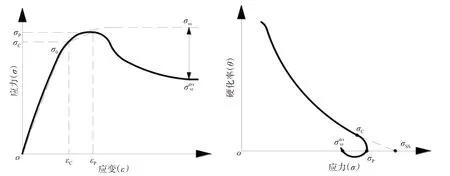
图4 热塑性变形中流动应力应变曲线及硬化率关系:(a) σ-ε;(b) θ-σFig.4 Stress-strain and hardening ratio of hot plastic deformation:(a) σ-ε;(b) θ-σ
在应变达到临界应变之前,即ε≤εc时。仅考虑加工硬化过程的位错积聚与动态回复过程的位错湮灭,利用K-M模型表示热加工过程中的位错湮灭[22],并建立流动应力与位错密度之间的方程为:
式(1)、式(2)中:ρ为材料位错密度;ε为应变值;ηh为材料硬化参数;ηr为材料软化参数;α为描述材料位错交互强度的参数,一般取0.5;b为柏氏矢量;μ为剪切模量,其表达式为:
式(3)中:T为成形温度;T0为环境温度;Tm为材料熔点,TC11钛合金为1 941~1 961 ℃;Cm为材料常数;CT为温度常数。
可通过TC11钛合金材料弹性模量求出其剪切模量:
式(4)中:E为弹性模量;ν为泊松比。对式(3)进行回归分析可求出Cm= 6.132×109、CT= 0.657。
将式(1)两边积分、变换得位错密度为:
式(6)中:ρ0为初始位错密度。得到在动态回复与加工硬化阶段流动应力本构方程如式(7)所示:
当TC11钛合金处于动态再结晶阶段,即ε≥εc时,采用动态再结晶分数描述热变形条件下动态再结晶发生程度,并通过动态再结晶动力学方程建立其与流动应力及应变之间的关系,如式(8)所示[21,23]。
式(8)中:σss为饱和应力;为稳态流动应力;εc为动态再结晶临界应变;εp为峰值应变;n、K为材料常数。
如图4(b)所示,在塑性成形过程中流动应力对应变的导数必定存在由于动态再结晶导致的应力增加变缓的拐点,该拐点与动态再结晶临界条件相对应[22,24]。图5所示为TC11钛合金在900~1 050 ℃、应变速率0.1 s-1条件下试验数据所做出的应力-硬化率曲线。由于拐点不易确定,可通过对θ-σ关系求一阶导数,由dθ/dσ-σ的最小值求得[25-26]。

图5 不同温度下硬化率曲线(̇= 0.1 s-1)Fig.5 Hardening ratio at different temperatures (̇= 0.1 s-1)
通过对流动应力应变进行拟合并求导硬化率与流动应力曲线,曲线拐点即对应动态再结晶临界条件,曲线与y=0直线的交点即流动应力应变曲线的峰值。求得TC11钛合金在不同应变率及温度条件下材料的特征应力,由此获得TC11钛合金峰值应力及应变σP、εP和临界应力及应变σc、εc,如表2和表3所列。
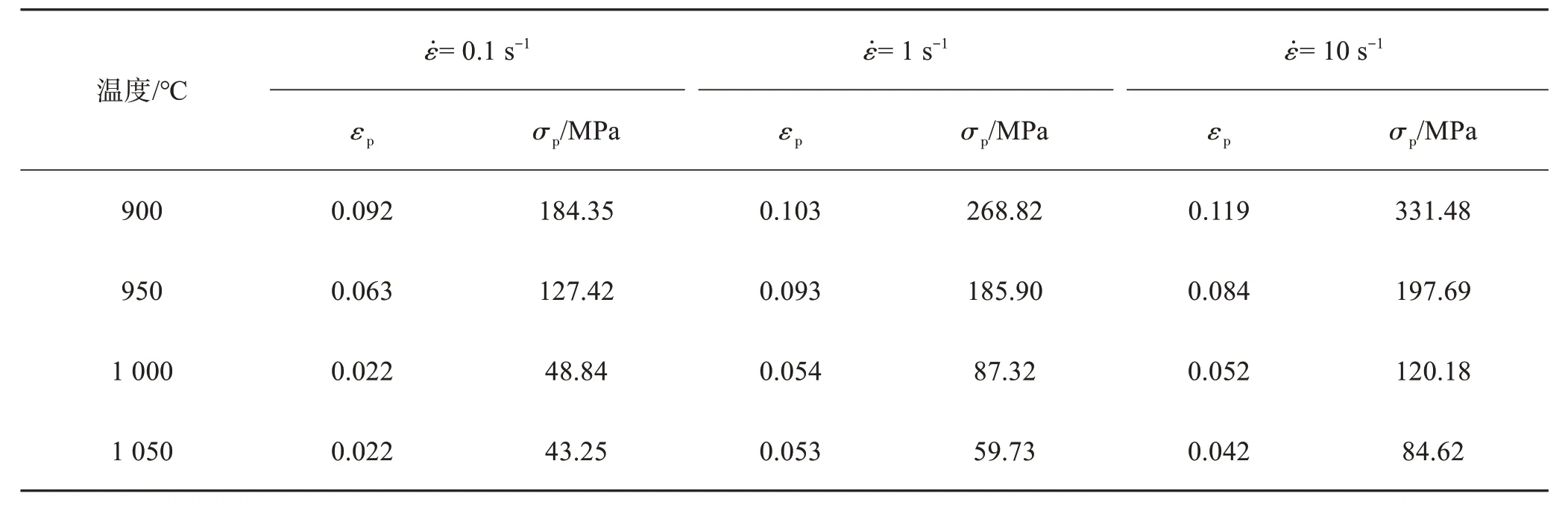
表2 TC11钛合金峰值应力及应变Table 2 Peak stress-strain of TC11 titanium alloy
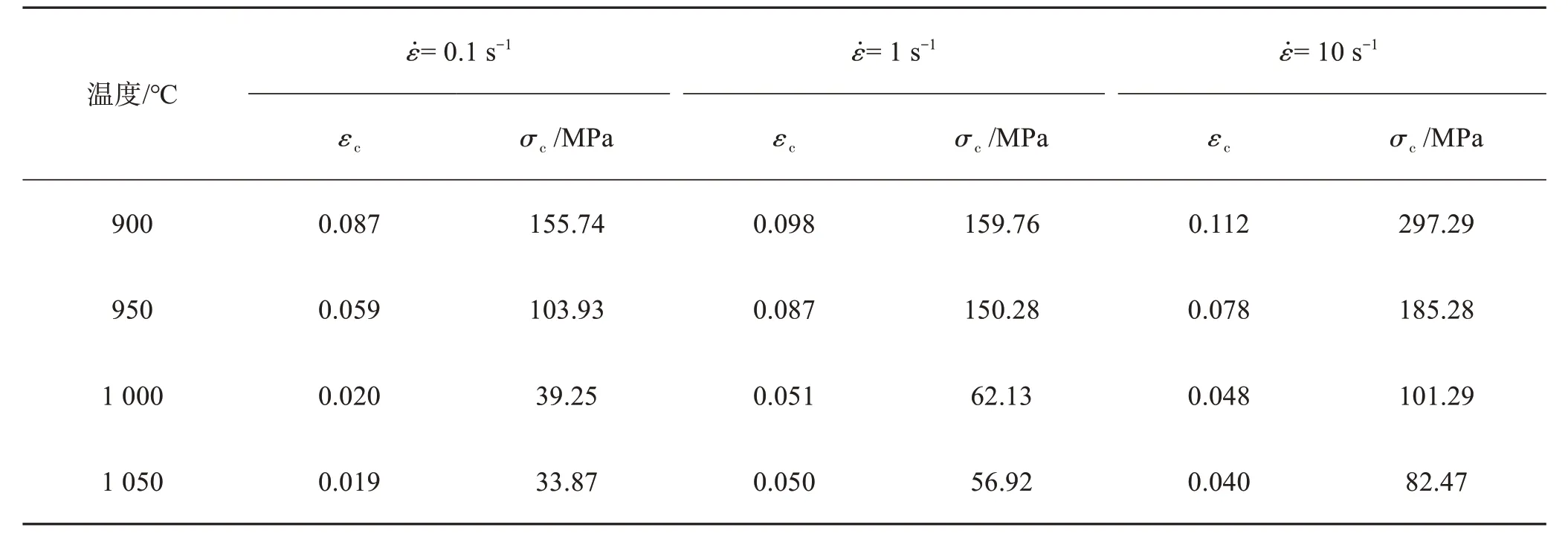
表3 TC11钛合金临界应力及应变Table 3 Critical stress-strain of TC11 titanium alloy
当ε≥εc时,将式(8)等式两边做变换可得动态再结晶阶段流动应力,如式(9)所示:
因此,得到考虑动态回复与动态再结晶的TC11钛合金高温本构模型如式(10)所示:
由于临界应变与变形速率及变形温度相关,因此基于Arrhenius方程建立临界应力-应变模型与峰值应力及应变模型得:
根据已有试验数据求解Ac和nc得:
据此可求得材料硬化系数ηh与材料软化系数ηr。建立其与应变速率及变形温度之间的关系,得到两个系数的表达式为:
为求解材料常数K,对等式将两边取对数得:
根据高温平面应变压缩试验结果及式(14)进行回归分析,即可获得材料常数K、n。根据应变项优化的TC11钛合金高温本构模型的预测结果,最终确定当应变速率̇≤0.01 s-1时,K=0.034、n=3.59;当应变速率̇>0.01 s-1时,K=0.47,n=2.04,具有相对较好的预测精度。
4 预测结果分析和讨论
图6和图7所示为TC11钛合金在不同参数条件下通过考虑动态回复与动态再结晶的流动应力模型计算所得预测值和试验值的比较情况。由图7可见,在大多数工艺参数条件下,预测情况较好;部分条件下,预测值比试验值略高。通过建立位错密度模型和再结晶分数模型并结合金相图片分析可知,升高温度会促进材料变形过程中位错的运动,但同时也会影响TC11钛合金的相转变速度。应变速率的增加在快速累积位错的同时也减少了变形所用的时间,这导致高应变速率条件下再结晶晶粒长大、两相组织转变等进程均受到了限制。
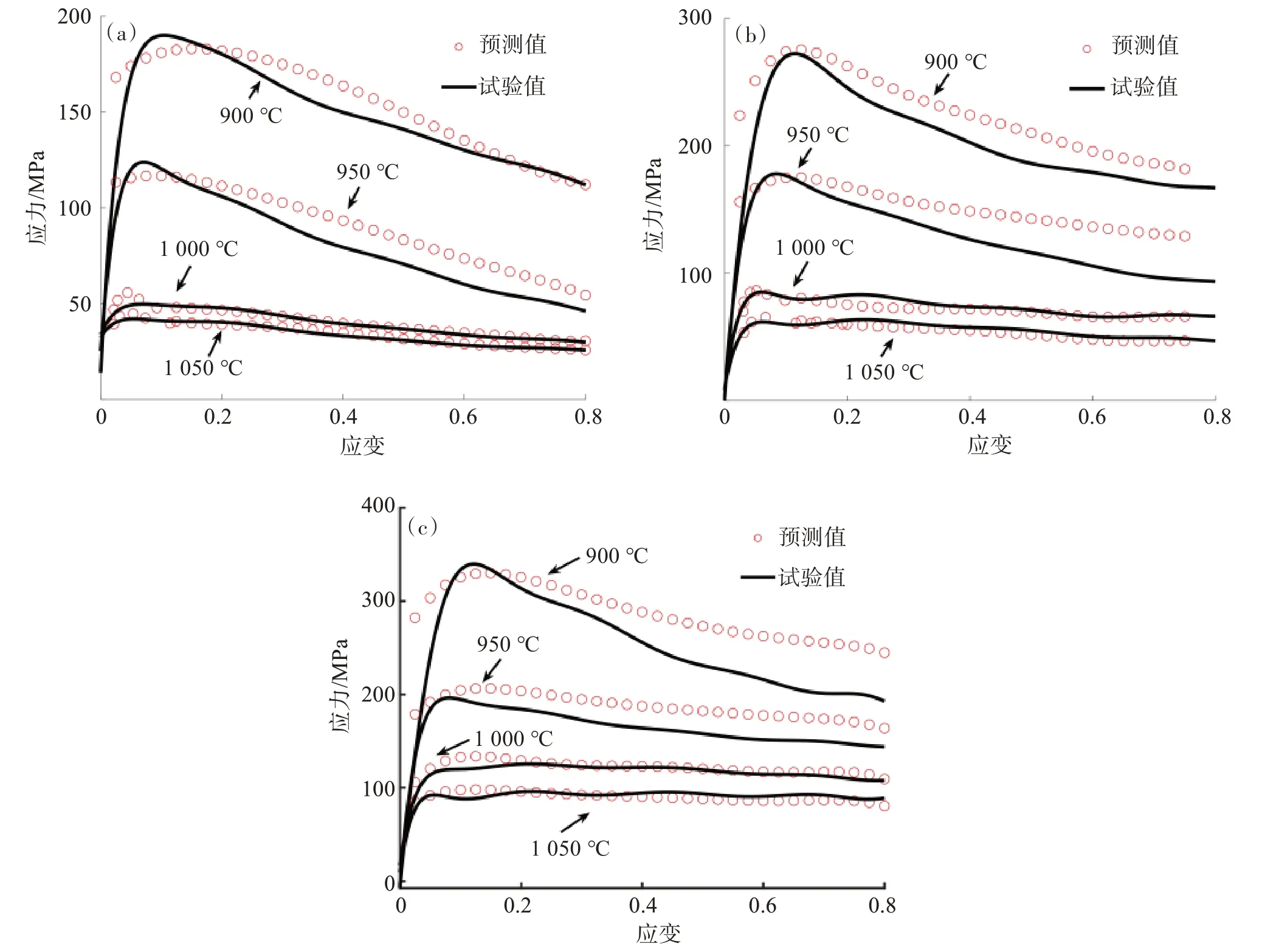
图6 试验值与考虑动态回复与动态再结晶本构模型预测值的对比:(a)̇= 0.1 s-1;(b)̇ = 1 s-1;(c) ̇ = 10 s-1Fig.6 Comparison of predicted value of dynamic recovery and dynamic recrystallization high-temperature constitutive model with test value:(a) ̇= 0.1 s-1;(b) 1 s-1;(c)̇= 10 s-1
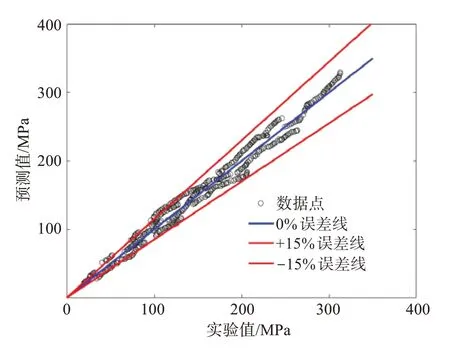
图7 TC11钛合金流动应力值的预测值与试验值的对比Fig.7 Comparison of predicted value of flow stress in TC11 titanium alloy with test value
曲线在变形温度1 000 ℃与1 050 ℃时预测结果较好,这是由于此时材料组织相变较充分,再结晶现象成为影响流动应力的主要因素。变形温度分别为900 ℃与950 ℃时,试样在热变形过程中发生了大量相变,使得再结晶分数模型预测范围内预测值普遍高于试验值,在900 ℃、ε̇= 10 s-1与950 ℃、ε̇ = 1 s-1条件下最明显。在900 ℃、ε̇ = 0.1 s-1与950 ℃、ε̇ = 0.1 s-1时,结合金相图片与流动应力曲线分析可知,在变形过程中可能发生了多次再结晶,再结晶导致的流动应力下降相较于其余相同温度下的试验组更多,因此预测结果更准确。
对比动态回复与动态再结晶的流动应力本构模型预测值与试验值(图7)可知,正负偏差控制在15%以内,预测精度较好。其中,模型的相关性系数R=0.989,平均相对误差E=6.53%。应变速率分别为0.1、1、10 s-1时,平均相对误差分别为6.37%、5.24%、3.19%;变形温度分别在900、950、1 000、1 050 ℃时,平均相对误差分别为6.98%、7.43%、6.32%、6.18%,总的平均相对误差为6.84%。在动态回复与动态再结晶阶段,模型的整体预测值较高,本构模型预测值与试验值基本吻合。所得动态回复与动态再结晶流动应力模型能够地准确预测TC11钛合金高温流变行为。
5 结论
通过热压缩试验对TC11钛合金在热变形过程中的流动应力及动态回复与动态再结晶行为进行了研究,得到了以下结论:
1)TC11钛合金的流动应力先随应变增加而增大,在应力达到峰值应力后,应力又明显下降,在ε≥0.6时应力下降缓慢,最终趋向于一个稳定值;整体曲线先后呈现动态回复和动态再结晶两种特征,最后达到动态平衡状态。
2)在应变速率一定时,热变形后的TC11钛合金组织中α相含量随变形温度升高而降低,在高应变速率、温度达1 050 ℃时几乎完全转变为β相;变形温度分别为900、950 ℃时,随着应变速率的增加,组织中再结晶晶粒尺寸先增大后因变形时间短,再结晶未完全发生而减小;变形温度分别达1 000、1 050 ℃时,组织中随应变速率增加,α相含量大量减少,组织再结晶现象加剧,晶粒发生细化。
3)分别采用K-M位错密度模型与动态再结晶分数表征TC11钛合金动态回复与动态再结晶的高温流变行为。动态回复与动态再结晶的流动应力高温本构模型与试验结果一致,其平均相对误差为6.53%,相关性系数R= 0.989,模型整体预测结果误差小于15%,具有较好的预测性能。
