考虑多维随机地震作用的钢烟囱可靠度分析
2024-03-13姜云木王鑫鹏
闫 龙,胡 博,姜云木,王鑫鹏
(1. 武汉工程大学 土木工程与建筑学院,湖北 武汉 430074; 2. 南宁职业技术学院 建筑工程学院,广西 南宁 530000;3. 青岛理工大学 土木工程学院,山东 青岛 266520)
0 引言
烟囱是一种为热烟气或烟雾提供通风的结构[1],在火电、冶金等工业领域具有重要地位。精确地评估烟囱结构在地震作用下的可靠性对保证工厂人员及财产安全极其重要。地震作为破坏力巨大的自然灾害之一[2-4],具有显著的随机性及多维性[5-6],因此,在工程实际中应充分考虑地震动的上述特性。
对于随机地震动,模拟方法一般有谱表示、本征正交分解等[7-9]。谱表示和本征正交分解因其理论完善、计算简单,应用较为广泛。然而,上述方法均是在Monte Carlo方法的框架之内,通过对一系列随机变量进行反复抽样,最终生成满足一定模拟精度要求的样本。此外,模拟精度与抽样的数量存在负相关关系,较难实现大型复杂结构抗震可靠性的精细化分析[10]。针对以上问题,姜云木等[11]、RUAN等[12]通过引入随机函数约束形式,尽可能地降低了随机变量个数。同时,在概率层面实现了随机地震动的精细化模拟。
地震动的多维特性对烟囱结构的动力响应同样至关重要。周长东等[13]以一座高240m的某钢筋混凝土烟囱为例,将地震动分别以一维、二维和三维形式作用于其上。结果表明,三维地震动作用下烟囱发生损坏及倒塌的风险更大。田苗旺[14]分析了在一维、二维和三维地震动作用下,240 m高的钢混烟囱结构发生倒塌概率为50%时所对应的峰值加速度依次为1.2、0.75、0.375g;结构最容易出现损伤的位置基本相同,均为结构底部(0~20 m),中部(90~120 m),中上部(160~200 m)。何乡等[15]认为在不同性能极限状态下,仅考虑一维地震动作用会严重高估工程结构的抗震性能,当考虑三维地震动作用时,结构的破坏概率将会增加。
以上均采用的是确定性方法对结构进行抗震性能分析。然而,无论是初始条件、外部激励还是系统参数均具有强烈的随机性。因此,结构的动力响应是一个随机过程。结构随机动力反应与可靠度分析是工程结构安全性评价的基础。目前,结构动力可靠性的分析方法可大致分为两大类:扩散过程理论[16]和跨越过程理论[17]。其中,扩散过程理论存在着求解高维偏微分方程的困难,而跨越过程理论无法确保较好的精度。可见,传统的可靠度分析方法难以在保持精度的同时高效地获取结构可靠度[18]。近年来,LI等[19]提出的概率密度演化理论较好地解决了上述问题。该理论的基础是随机动力系统的概率守恒,通过对确定性动力时程反应进行分析,其可以捕获结构响应的概率密度函数。
综上,本文考虑地震灾害的随机性和多维性,选用了一种更加保守的可靠度评价指标,运用概率密度演化方法,对某厂区一座自立式钢烟囱结构进行了动力响应分析及可靠度评价。
1 多维地震动随机向量过程的降维模拟
对于1V-3D的多维地震动,可将其视为3V-1D的非平稳随机向量过程X(t)=[X1(t),X2(t),X3(t)],其中,1、2、3依次表示多维地震动的x、y、z这3个方向。X(t)的双边演变功率谱密度矩阵可定义为
(1)
式中,Si(ω,t)和Sij(ω,t)分别为i方向分量的自演变功率谱和i,j方向分量间的互演变功率谱。其中,Sij(ω,t)可表示为
(2)
式中γij(ω)为多维地震动i,j方向分量间的相干函数。根据松岛丰模型[5]可知,多维地震动不同分量间的相干函数可定义为
(3)
对演变功率谱矩阵S(ω,t)进行分解[9],进一步可得
S(ω,t)=D(ω,t)γ(ω)DT(ω,t)
(4)
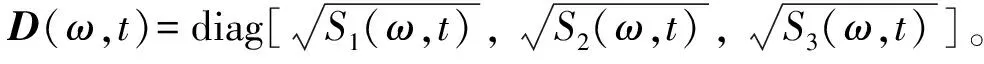
(5)
式中λi(ω)、ψi(ω)依次为γ(ω)的特征值和特征向量。
综上,根据文献[20],可得多维地震动i方向分量的POD表达式为
(6)
式中:N为频率截断项数;Δω为频率离散步长;χir(ωk)和Zir(ωk)分别为特征向量元素ψi(ω)=χir(ωk)+iZir(ωk)中的实部和虚部;{Rrk,Irk}为一组标准正交的随机变量,且满足以下基本条件:
(7)
根据降维理论[11-12],可将{Rrk,Irk}定义为如下的随机函数形式为
(8)
式中:Θi(i=1,2)为区间(0,2π)上的基本随机变量,其样本集可表示为Θi=[2πθ1,2πθ2,...,2πθnsel],θn为区间[0,1]上均匀分布的代表性点集,可利用数论方法进行选取[21],nsel为代表性点集的数量。此外,还需要进行(s,l)→(r,k)的确定性随机序列变换。这一确定性的一一映射变换可以通过Matlab工具箱中的rand(‘state’,1)和temp=randperm(3×N)函数来实现。如此,便可唯一确定正交随机变量{Rrk,Irk}的值。
2 结构整体可靠度评价
POD-降维方法尽最大潜力降低了随机变量的个数,为数论方法的应用提供了可能。数论方法选取的点集具有良好的整体均匀性,且每个代表性点的赋得概率为1/nsel,即:每个代表性样本的赋得概率为1/nsel。基于此,可进一步地与概率密度演化理论及等价极值分布的首次超越破坏可靠度评价方法相结合,对自立式钢烟囱结构进行整体可靠度评价。
2.1 概率密度演化理论
对于具有n个自由度的工程结构系统,在利用有限元分析求解随机动力响应时,多自由度结构系统动力方程为
(9)
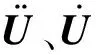
现将需要且系统涉及到的相关结构响应表示为Z(t)。对于构成的概率保守系统(Z,Θ),其包含了所有随机性。若联合概率密度函数pZΘ(z,θ,t)已知,则广义概率密度演化方程可表示为[18-19]
(10)
(11)
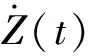
2.2 基于极值分布的可靠度计算
与规范不同,本研究将自立式钢烟囱结构分为若干段,将各段相对水平位移角Φj(t)作为结构整体可靠度的评价指标。由极值事件原理可知,第j段结构的可靠度可表示为
RT,j(φ0)=Pr{Φj,max<φ0} (j=1,2,…,Nr)
(12)
(13)
式中:φ0为给定的阈值;T为地震动持时;Φj,max为第j段的相对水平位移角极值。
由等价极值事件可知,结构的整体动力可靠度即为[18-19]
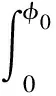
(14)
(15)
式中Φmax为所有段结构相对水平位移角的等价极值。
3 工程概况及分析
3.1 工程概况
某工业城市的自立式钢烟囱结构,烟囱高60 m,底部直径为9 m,材料为Q235,钢材的屈服强度为235 N/mm2,弹性模量为E=2.06×106N/mm2,密度为ρ=7.85×103kg/m3。现沿高度方向将其划分为8段,各段尺寸如表1所示。相应结构的模态结果如表2所示。自立式钢烟囱ANSYS有限元模型如图1所示。
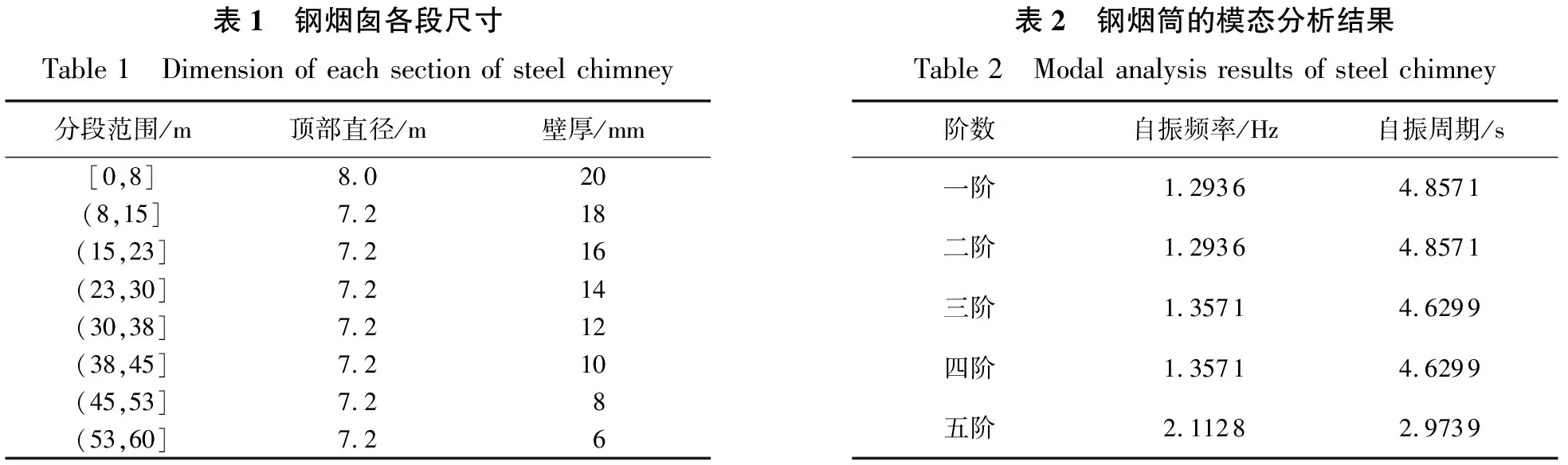
表1 钢烟囱各段尺寸Table 1 Dimension of each section of steel chimney分段范围/m顶部直径/m壁厚/mm[0,8]8.020(8,15]7.218(15,23]7.216(23,30]7.214(30,38]7.212(38,45]7.210(45,53]7.28(53,60]7.26表2 钢烟筒的模态分析结果Table 2 Modal analysis results of steel chimney阶数自振频率/Hz自振周期/s一阶1.29364.8571二阶1.29364.8571三阶1.35714.6299四阶1.35714.6299五阶2.11282.9739
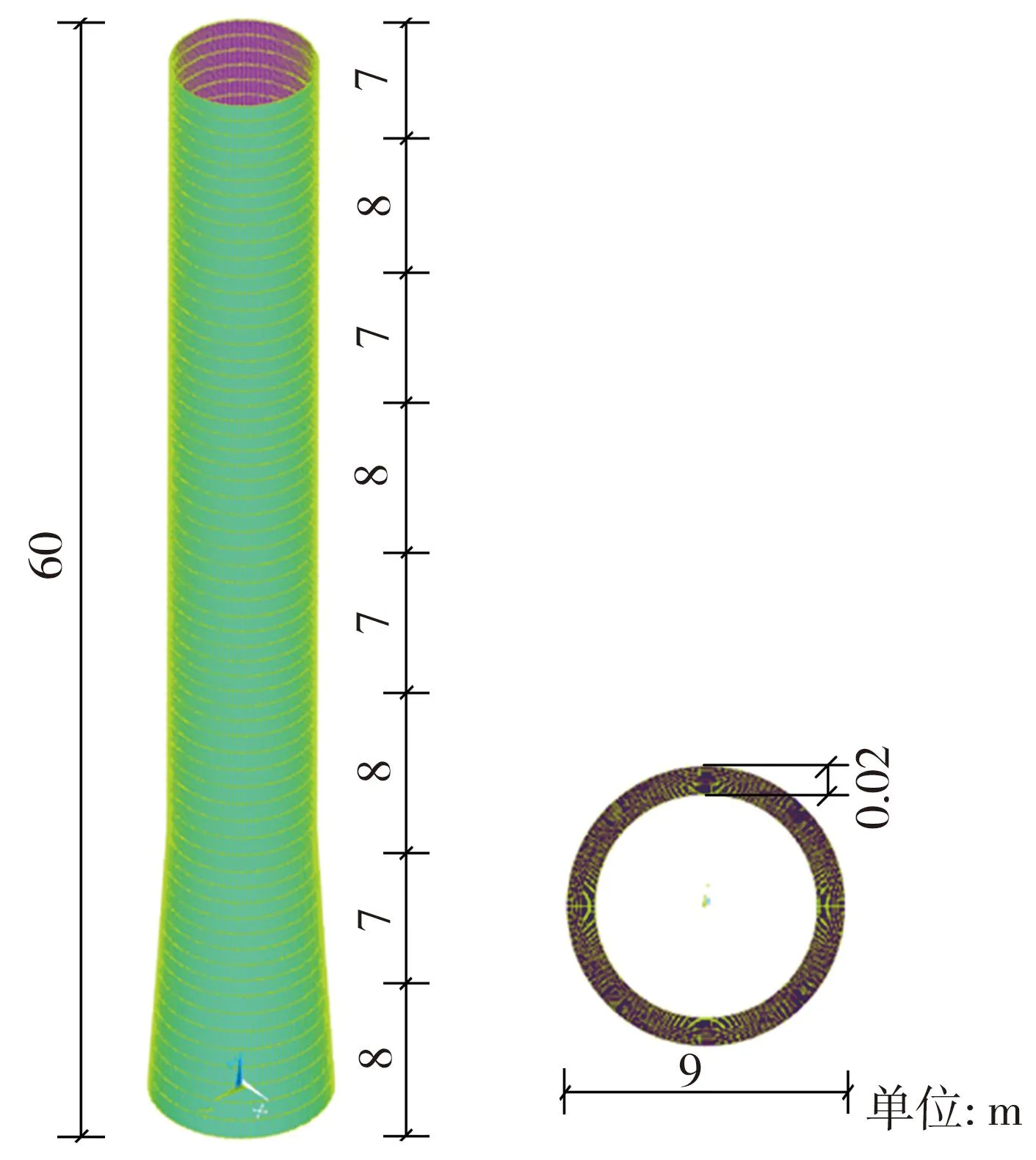
图1 自立式钢烟囱有限元模型Fig.1 Finite element model of self-supporting steel chimney
3.2 多维随机地震动模拟
进行多维地震动模拟时,本文功率谱选用经典的双边Kanai-Tajimi模型[21]为
(16)
式中:ωg,i和ξg,i分别为多维地震动i方向分量的场地土卓越圆频率和阻尼比;S0,i为多维地震动i方向分量的强度因子,可表示为[22]
(17)
对于多维地震动x方向分量的功率谱参数取值,可参考文献[23]。其它方向分量的功率谱参数与x方向分量的功率谱参数取值保持以下关系[20]:
ωg,1=1.58ωg,2=1.58ωg,3ξg,1=ξg,2=ξg,3r1=1.5r2=1.5r3
(18)
为实现地震动的非平稳特性,本文调制函数采用基于Amin-Ang建议的四段模型[24]为
(19)
式中,t0,i、t1,i、t2,i和ci依次表示多维地震动i方向分量的上升段、平稳段和衰减段的起始时间以及衰减段的衰减速度。其模型参数取值可参考文献[25]。
本算例以II类场地,8度罕遇地震为例。截断频率取ωu=240 rad/s,频率离散间隔取Δω=0.15 rad/s;模拟持时取T=25 s,时间离散间隔取Δt=0.01 s。功率谱及调制函数相关参数如表3所示。
如此,便可利用POD-降维方法进行多维地震动的模拟。生成的第50条多维地震动的代表性样本如图2所示。经对比发现,x方向分量与y方向分量的幅值、频谱及持时较为一致,而z方向分量则表现出高频分量增多、幅值减小且持时增长的现象。这符合工程实际上对多维地震动的认知。因此,可以认为本文建议的多维地震动参数模型具有一定的工程适用性。
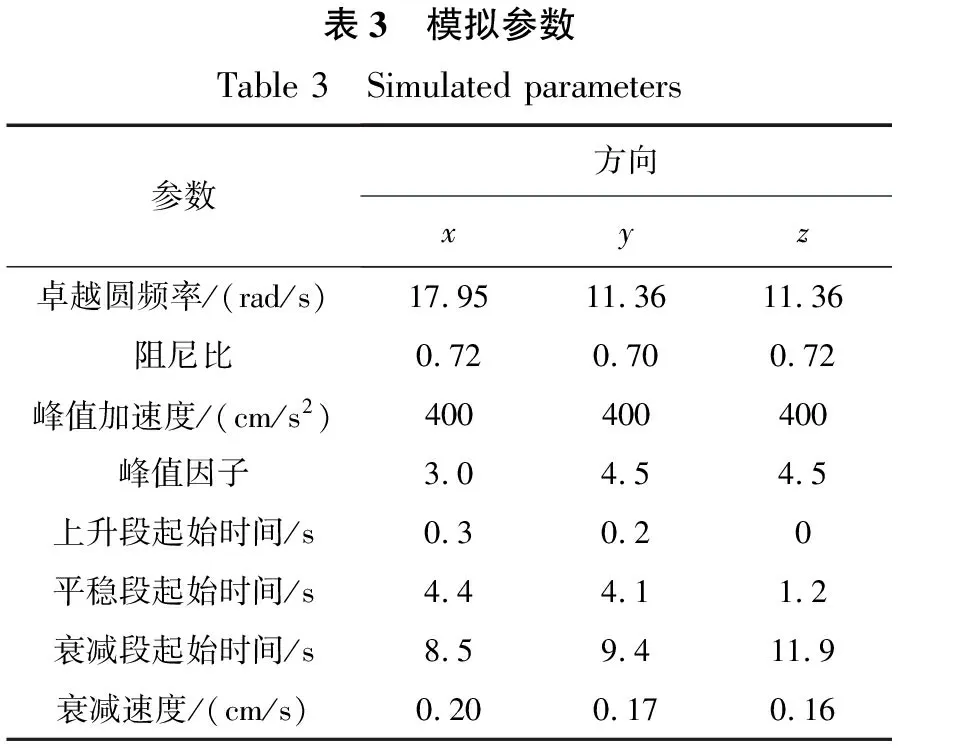
表3 模拟参数Table 3 Simulated parameters参数方向xyz卓越圆频率/(rad/s)17.9511.3611.36阻尼比0.720.700.72峰值加速度/(cm/s2)400400400峰值因子3.04.54.5上升段起始时间/s0.30.20平稳段起始时间/s4.44.11.2衰减段起始时间/s8.59.411.9衰减速度/(cm/s)0.200.170.16图2 代表性样本Fig.2 Representative samples
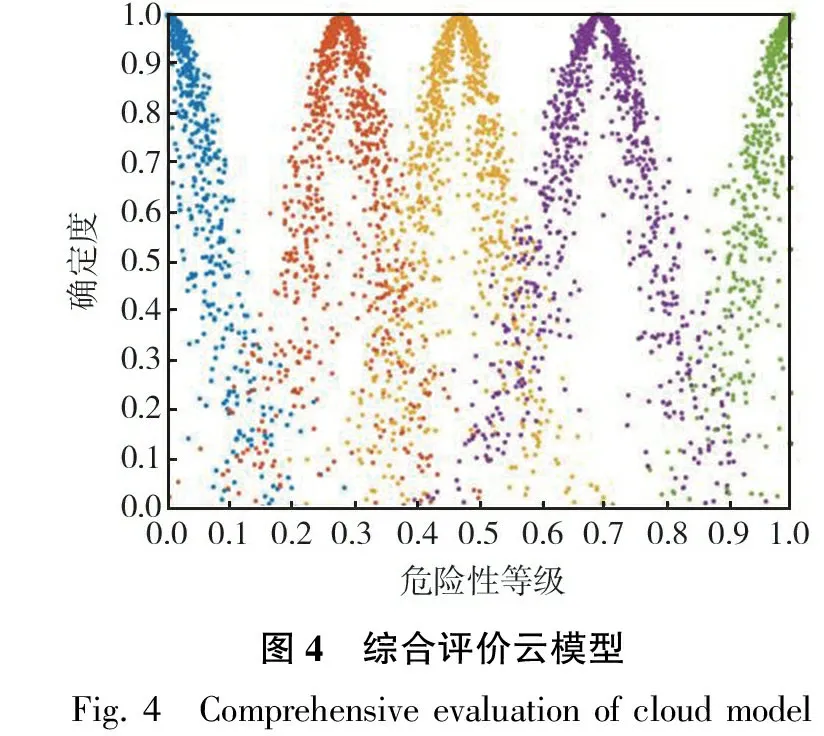
为了证明POD-降维方法的精确性,进一步对模拟样本的一阶、二阶统计量进行分析。经计算,得到x、y、z方向的均值相对误差均为0%,标准差相对误差依次为4.96%、4.59%、3.74%,以上平均相对误差均小于5%,说明所生成的多维地震加速度样本可以用于工程实际。3种典型时刻下的功率谱模拟值和目标值的对比效果如图3所示,可以看出,模拟值与目标值拟合良好,验证了POD-降维方法的精确性。
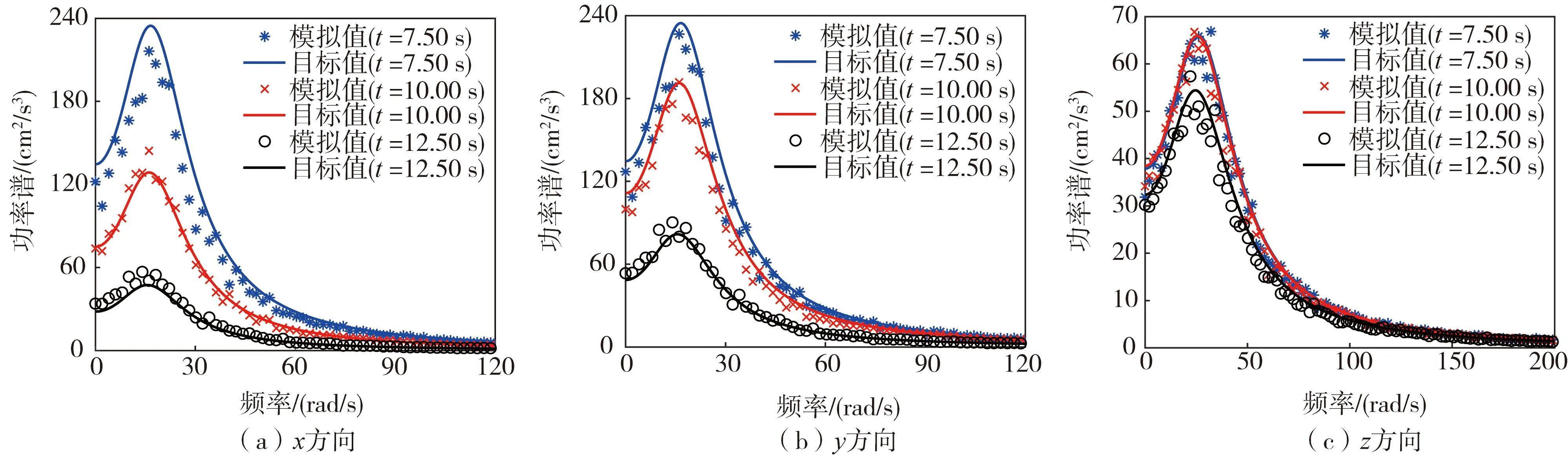
图3 不同时刻多维地震动分量功率谱与目标谱比较Fig.3 Comparison of power spectrum and target spectrum of multi-dimensional ground motion components at different times
3.3 结构动力响应及可靠度计算
将生成的多维随机地震动场对上述自立式钢烟囱进行233次确定性结构动力响应分析。图4(a)和(b)依次为x方向和y方向233条代表性样本对应的结构顶点位移的极值。由图可知,x方向和y方向结构反应的最大极值均在0.8 m左右,对应的样本均在第五十条附近。第一百条代表性样本作用下结构各段顶部位移时程曲线如图5所示。不难看出,大约在第六秒时,结构的动力响应最为强烈,这是由于输入的多维随机地震动激励在第六秒时正处于峰值最大时刻。同时,顶点位移极值曲线的波动情况及代表性样本对应的结构反应时程曲线的演化趋势均说明了生成的多维地震激励具有明显的随机性。

图4 顶点位移极值Fig.4 Extreme value of top displacement
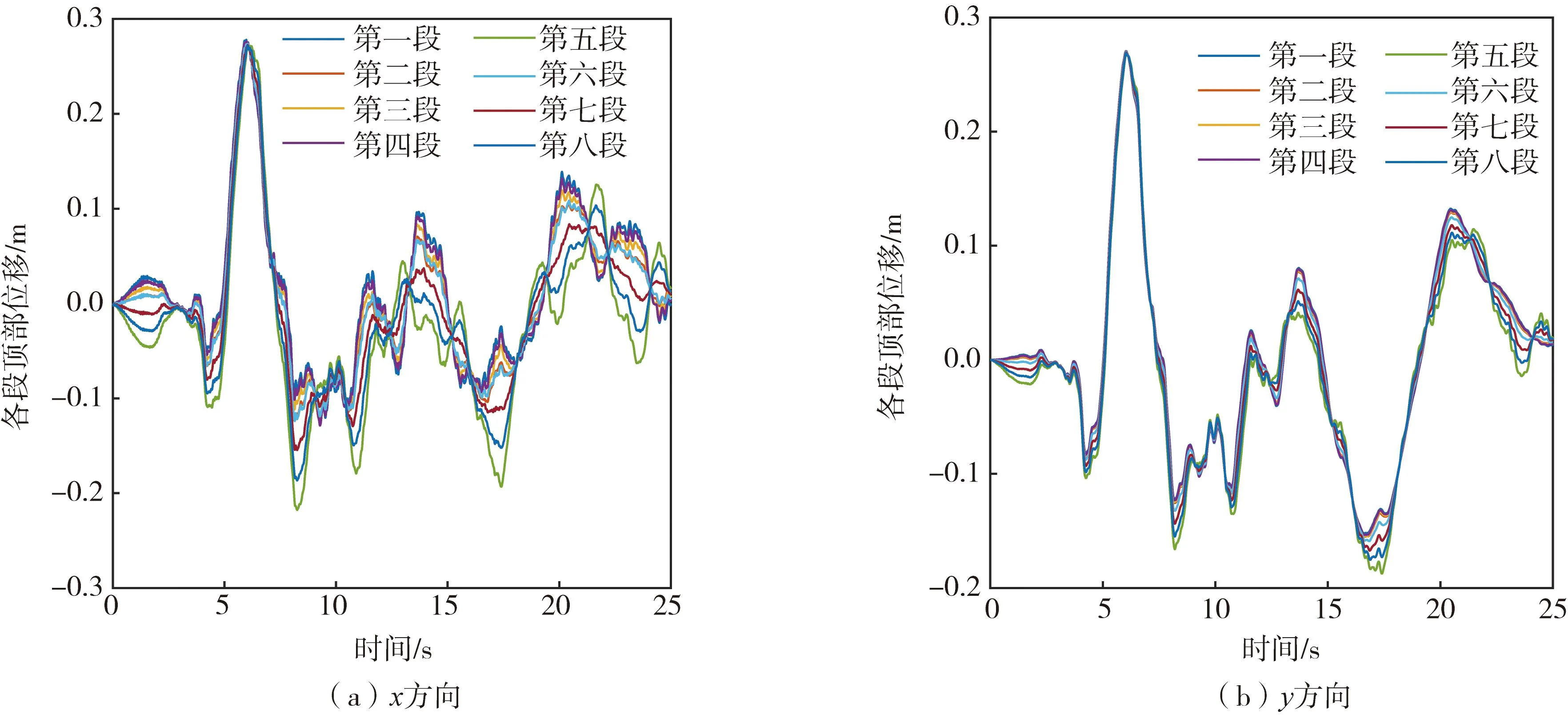
图5 第一百条代表性样本对应的结构反应Fig.5 Structural response from the 100th representative sample
参考GB 50135—2019《高耸结构设计标准》[26]中规定的将高耸结构顶部水平位移角限值作为可靠度评价指标,此处,将结构各段相对水平位移角限值作为结构整体可靠度评价指标。
首先,以结构顶点水平位移角1/50为阈值。根据GB 50011—2010《建筑抗震设计规范》[27]相关规定,对自立式钢烟囱结构抗震设防的第三水准进行分析。运用概率密度演化理论及等价极值分布的首次超越破坏可靠度评价方法,计算罕遇地震影响中钢烟囱结构x方向与y方向的可靠度。2个方向的可靠度均为100%,抗震性能满足工程实际的要求,如图6所示。进一步地,计算233条代表性样本对应的各段相对水平位移角极值,如图7所示。由图可知,无论是x方向还是y方向,相对水平位移角极值的最大值出现在第五段。由此猜测,直立式钢烟囱的薄弱部位可能将出现在该段。

图7 各段相对水平位移角极值Fig.7 Extreme value of relative horizontal displacement angle of each segment
同样地,以结构相对水平位移角1/50为阈值,将自立式钢烟囱截面相对水平位移角作为结构整体可靠度评价指标,计算钢烟囱结构各段x方向和y方向的可靠度,如图8所示。将图6与图8进行对比,以各段相对水平位移角为限值的可靠度评价得到的结构整体可靠度为99.98%,低于规范中以结构顶点水平位移角限值为指标的可靠度评价。此外,由图8可知,第五段和第六段的可靠度明显小于其它各段,在抗震设计时应重点进行关注;若为在役结构,应在该段采取结构加固措施以确保结构的抗震安全。

图6 累计分布函数Fig.6 Cumulative distribution function
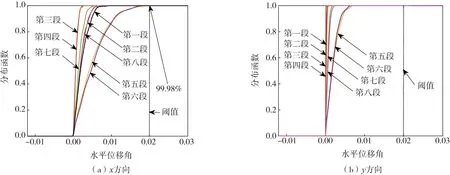
图8 各段累计分布函数Fig.8 Cumulative distribution function of each segment
综上分析,除地震动特性、结构类型等客观因素外,工程结构可靠度评价方法的主观选择也是极为重要的。不同可靠度评价方法所获取的可靠度数值及相关信息的丰富程度具有差异性。
4 结论
为了从整体角度把握多维随机地震动作用下钢烟囱结构的抗震性能,本文运用基于随机函数约束和数论选点的POD-降维方法,模拟了233条具有已知赋得概率的非平稳多维随机地震动加速度时程;同时,建议了一种新的可靠度评价指标。以某工业城市的钢烟囱结构为工程对象,对其可靠度进行分析,得到如下结论:
1)给定参数关系和多维地震动相干函数模型,由POD-维方法模拟得到的地震动样本,其竖向分量与水平向分量相比,持时更长,幅值更小,低频成分更多,符合工程上对多维地震动的认知。验证了本文参数关系和相干函数模型的有效性。
2)模拟样本的均值相对误差和标准差相对误差均小于4.96%,且典型时刻下功率谱模拟值与目标值对应良好,证明了POD-降维方法的精确性。同时,模拟的非平稳多维地震动代表性样本具有已知赋得概率。这为工程实践中在概率密度层面进行动力响应及抗震可靠性分析奠定了良好基础。
3)与规范中仅考虑高耸结构顶部水平位移角限值相比,本文建议的可靠度评价指标更加保守。进行分段处理后,对结构整体抗震性能的把握更具精确性,可为设计施工、维修加固等工程实际提供参考。
