基于博弈论和云模型的滑坡危险性评价
2024-03-13余岭燕郭荣昌
余岭燕,郭荣昌,张 蕊
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
0 引言
中国是世界上地质灾害多发的国家之一,而滑坡是最主要的自然灾害形式之一,往往会给人类带来极大的威胁[1]。据统计,2021年我国共发生地质灾害4772处,造成80人死亡,11人失踪,直接经济损失32亿元,其中滑坡灾害就有2335处,占比48.93%。因此,开展滑坡危险性评价的研究,对地质灾害防治、风险防控具有重要意义。
近年来,许多专家学者针对滑坡危险性展开了研究。王念秦等[2]利用spearman对各因子进行相关性分析,并采用不同基函数下的SVM模型进行危险性评价,结果表明RBF-SVM模型的精度最高;吴常润等[3]采用FR与LR融合模型对双柏县进行滑坡易发性评价,结果表明融合模型比单一模型预测率高9.2%;黄发明等[4]采用聚类分析和SVM对万州区滑坡进行易发性评价,结果表明聚类分析后的模型比未分类的模型具有更高的预测率;张洪吉等[5]采用一维卷积神经网络对芦山县进行滑坡危险性评价,评价精度高于90%;宋盛渊等[6]采用突变理论对潜在滑坡进行危险性评价,结果表明评判结果准确率较高;杨华阳等[7]采用加法和减法2种证据权,将九寨沟地震滑坡危险性划分为5个等级,从而更有效地预测滑坡危险性。然而,传统的研究方法很少同时引入定性概念与定量描述,而云模型能实现定性到定量的转换,同时只要滑坡数据足以提取特征,云模型也适用于单个滑坡危险性评价。滑坡灾害存在大量的不确定性,即地质环境、影响因子和评价过程中人为的不确定性,因此滑坡危险性评价是一个定性与定量相结合的课题。针对滑坡危险性评价中同时涉及定性概念与定量描述这一特点,通过云模型能够使滑坡危险性评价等级更直观、具体。
综上,通过应用博弈论和云模型,提出一种有效的滑坡危险性评价方法。首先由博弈论确定评价指标的最优权重,然后结合各评价指标的云模型,生成综合评价云,最后将综合评价云与评价标准云进行对比,根据最大相似度原则确定滑坡危险性等级,并用工程实例对该方法进行验证。
1 理论介绍
1.1 博弈论
博弈论,即对策论[8]是一种解决具有斗争性问题的运筹学方法,其基本思想是在多个决策主体中谋求一个最优组合状态,极小化各决策主体间的偏差,实现利益最大化[9]。
1.2 云模型
云模型概念由李德毅等[10]于1995年提出,是一种可以实现定性与定量转换的模型,能有效解决评价过程中的模糊性和随机性问题[11]。云模型的数字特征由期望Ex、熵En和超熵He构成,Ex表示云滴在论域中的期望,En表示不确定性的度量,即云滴范围,He表示不确定性的不确定性,即云滴厚度,通过正向云发生器生成云滴[12]。计算步骤为:生成一个以En为期望,以He为方差的正态分布随机数En′;生成一个以Ex为期望,以En′2为方差的正态分布随机数u;由式(1)计算该评价指标的隶属度μ(u),重复上述步骤直至生成N个云滴[13]:
(1)
对评价指标进行等级区间划分,设Cmin和Cmax分别对应于某一等级区间的最小值和最大值,则按式(2)计算云模型的期望Ex,按式(3)计算云模型的熵En。云模型的超熵He表示评价指标的模糊程度,一般为常数,全文取k=0.025。
(2)
(3)
1.3 权重计算方法
评价指标的权重可视为一个决策主体,最终权重应综合主观经验和客观信息的内在信息,借鉴博弈论思想,实现权重最优化。计算步骤如下:
1) 假设采用L种方法计算权重,则这L个权重进行任意线性组合,计算公式为
(4)
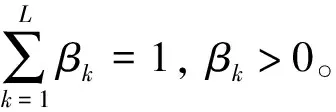
2) 计算权重系数为
(5)
式中:ωi为第i种方法计算的权重,根据矩阵微分性质,将式(5)展开:
(6)
3) 根据式(6)计算得到权重系数βk,归一化处理后代入式(4)即可得到最优权重。
2 滑坡危险性评价流程
基于博弈论和云模型的滑坡危险性评价流程如图1所示。
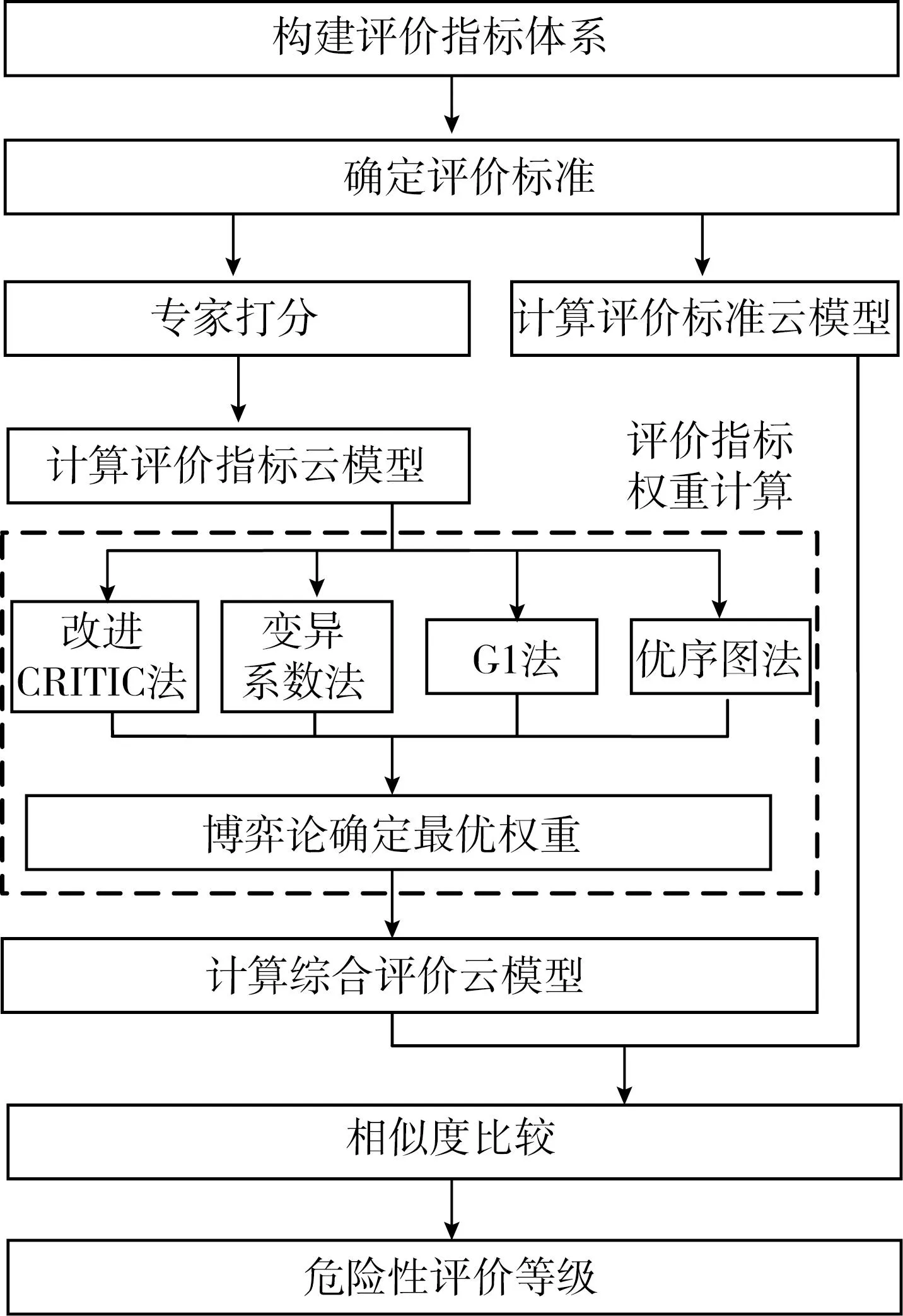
图1 基于博弈论和云模型的滑坡危险性评价流程Fig.1 Landslide hazard evaluation process based on game theory and cloud model
由图可知,博弈论和云模型的滑坡危险性方法主要步骤如下:
步骤1:构建评价指标体系;
步骤2:确定危险性评价标准,生成评价标准云;
步骤3:邀请专家对评价指标的重要性及滑坡等级进行打分,并生成各评价指标的云模型;
步骤4:分别采用改进CRITIC法、变异系数法、G1法和优序图法计算评价指标的权重,之后采用博弈论计算评价指标的最优权重;
步骤5:结合最优权重和各评价指标的云模型计算得到综合评价云模型;
步骤6:对综合评价云模型和评价标准云模型进行相似度比较,取相似度最大对应的等级为危险性评价等级。
3 滑坡危险性评价方法
3.1 评价指标体系构建
滑坡的诱因多种多样,既包括定量因素,又包括定性因素。在总结前人研究[14-16]的基础上,综合考虑专家经验,选取降雨(C1)、地层岩性(C2)、距断层距离(C3)、土地类型(C4)、坡度(C5)、高程(C6)、坡向(C7)、平面曲率(C8)、剖面曲率(C9)、到河流距离(C10)、植被覆盖率(C11)和人类活动(C12)等12个影响因子作为评价指标,其中选取24 h最大降雨量表示C1,距道路距离表示C12。自然断点法是一种广泛使用的分级方法,先采用自然断点法将连续型评价指标风险等级按自然断点法分为高风险(五级)、较高风险(四级)、中风险(三级)、较低风险(二级)和低风险(一级)这5个等级,然后依据项目实际情况并结合专家意见得到最终等级。对于离散型数据C2、C4的分级采用人为赋值法量化为数值,分类标准如表1所示。

表1 离散型评价因子分类标准Table 1 Classification criteria for discrete evaluation factors
3.2 评价指标体系权重计算
3.2.1 基于改进CRITIC方法的权重计算
CRITIC方法综合考虑了评价指标间对比强度和冲突性,是一种比熵权法更优越的客观赋值方法[17]。在此基础上,采用标准差系数改进CRITIC方法,计算步骤如下:
1) 选取m个滑坡、n个评价指标作为原始数据矩阵X,X=(xij)m×n,对原始数据进行标准化处理得到X*:
(7)
其中
(8)
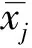
2)计算标准差系数
(9)
3) 计算标准化矩阵X*各评价指标间的相关性
(10)
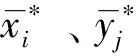
4) 计算评价指标的综合性系数
(11)
5) 确定各评价指标的权重
(12)
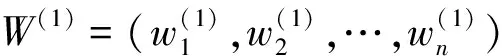
3.2.2 基于变异系数方法的权重计算
变异系数是标准差与平均值的比值,变异系数方法是一种简便的客观权重计算方法[18]。计算步骤如下:
1) 数据标准化,计算均值和标准差,由式(4)计算出评价指标的权重系数vj。
(13)
3.2.3 基于G1方法的权重计算
G1法是一种在层次分析法基础上改进的主观权重确定方法,计算过程无需构造矩阵,更为简便[19]。计算方法如下:
1) 对评价指标进行排序,即X1>X2>…>Xn,其中X1为专家认为对滑坡影响最大的评价指标,X2对滑坡的影响程度仅次于X1,以此类推。
2)计算相邻评价指标Xk-1与Xk的相对重要程度为
(14)
式中rk为重要程度比,参考值如表2所示。

表2 rk参考值Table 2 Reference values of rk
3) 计算排序后最不重要的评价指标的权重,即第n个评价指标的权重为
(15)
4)计算第k个评价指标的权重为
(16)
3.2.4 基于优序图方法的权重计算
优序图法是通过评价指标间的两两对比,得出重要性次序,计算步骤如下:
1) 对各评价指标进行重要性排序,并进行两两对比,即第j行和第i列相比,若第j行比第i列重要,则赋值Aij=1;若第j行比第i列同等重要,则赋值Aij=0.5;若第j行比第i列不重要,则赋值Aij=0。
2) 将各评价指标的评分赋值进行横向求和,得到最终得分Ai,计算公式为
(17)
(18)
3.2.5 博弈论权重计算
相较于其他组合权重计算方法,博弈论能够充分协调不同权重之间的冲突性,实现权重最优化。将4种基础权重值代入式(6),得到权重系数βk,然后将权重系数代入式(4),即可得到最优权重。
3.3 确定评价标准云
根据专家经验,将滑坡分为5个等级。为了方便计算,同时参考文献[20] ,按照等分原则将滑坡危险性区间[0,1]分为5个子区间,分别对应[0, 0.2](一级)、(0.2, 0.4] (二级)、(0.4, 0.6] (三级)、(0.6, 0.8] (四级)、(0.8, 1] (五级)。根据式(2)、式(3)计算评价标准云的数字特征,生成评价标准云模型图,如图2所示。
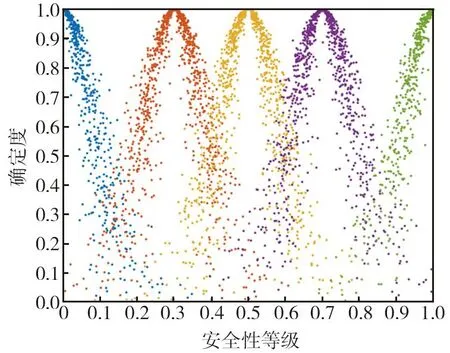
图2 评价标准云模型Fig.2 Cloud model of evaluation standard
3.4 确定综合评价云
根据式(2)、式(3)计算出各等级评价指标的云模型数字参数,然后结合各等级评价指标的云模型数字参数和对应的博弈论权重计算综合评价云模型,综合评价云模型的计算公式如下:
(19)
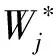
3.5 相似度计算
设C1、C2为2个评价云,将C1经过正向云发生器生成N个云滴(xi,μi),根据式(20)计算C1在C2中的隶属度μ′i,μ′i越大,2个云重复的云滴越多,即相似度越大[21]。相似度计算公式如下:
(20)
(21)
为了确保相似度计算结果的准确性,引入汉明距离计算相似度。汉明距离主要包括三部分:图像预处理、特征提取和哈希序列的生成[22]。基本步骤如下:
步骤1:图像预处理。将云模型各图像尺寸压缩至8×8,并计算像素平均值;
步骤2:特征提取。将每个像素与平均值比较,大于平均值的赋值1,反之赋值0;
步骤3:生成哈希序列。将特征按一定次序组合在一起,即哈希序列。
计算2个哈希序列的汉明距离(即异或运算)得到相似度,汉明距离越小,相似度越大。
4 实例验证
选取某铁路雨城至天全段为研究区,该段为在建铁路,全长76.3 km,位于四川省雅安市。研究区地势西高东低,海拔多在500~5000 m,是青藏高原向成都平原的过渡地带,相对高差较大,地貌结构不稳定,极易发生滑坡。
4.1 评价指标体系
为了验证博弈论和云模型的有效性,选取研究区上滑坡点不同时间的数据进行滑坡危险性评价,基于ArcGIS选取30 m×30 m的栅格单元作为评价单元,共3231×4333个栅格单元,评价指标的数据来源如表3 所示,部分数据如表4所示。
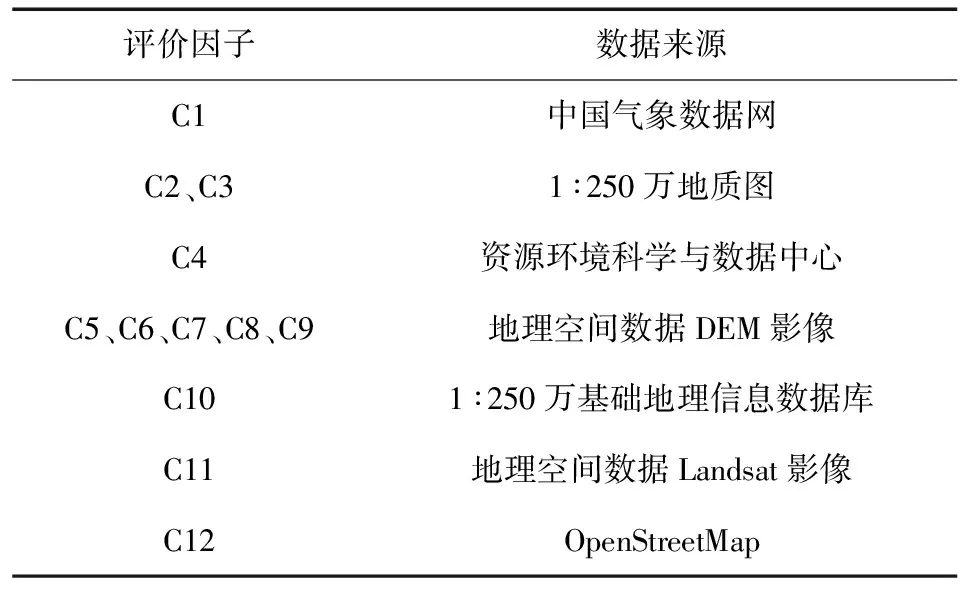
表3 评价指标数据来源Table 3 Data sources of evaluation indicators
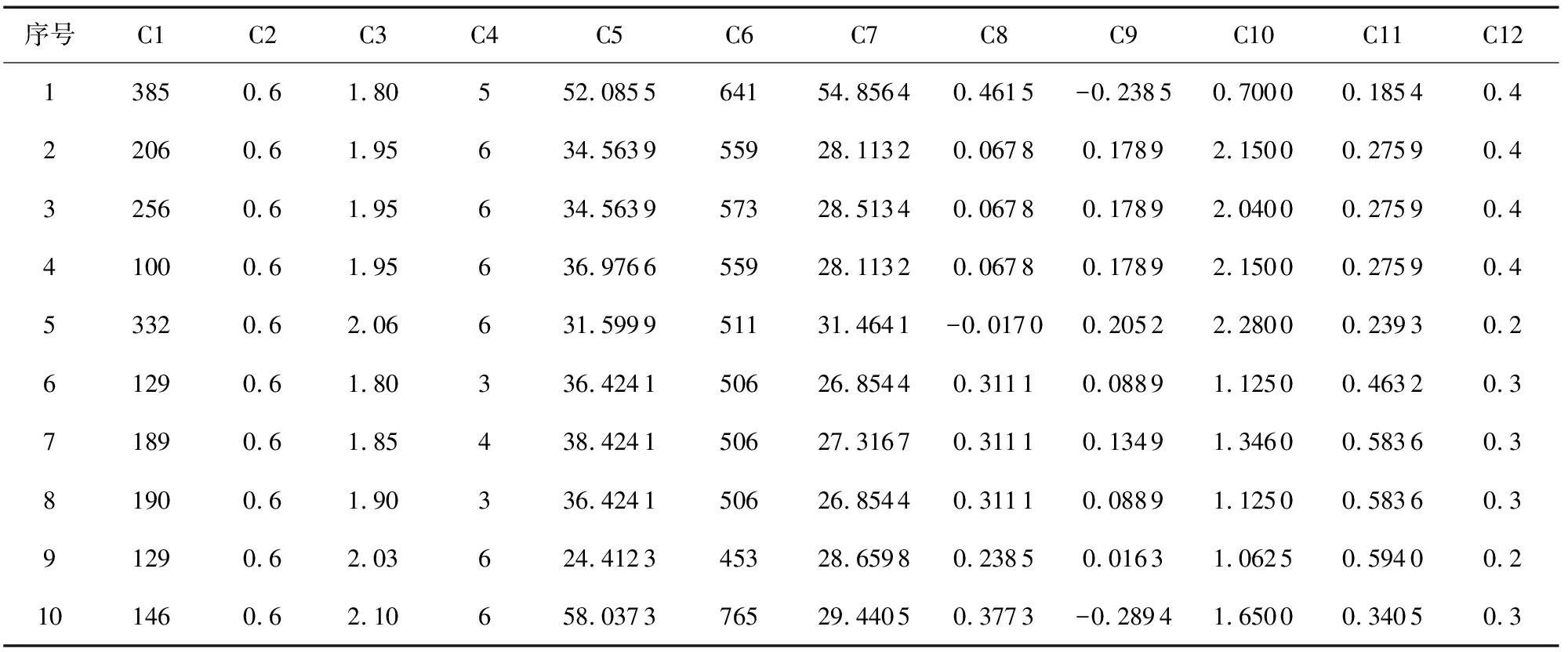
表4 评价指标数据Table 4 Evaluation index data
首先采用自然断点方法对每个评价指标进行分级,然后根据式(2)、式(3),计算各评价指标的数字特征,如表5所示,归一化后生成云模型,由于篇幅有限,仅列举降雨(C1)与地层岩性(C2)云模型,如图3(a)和图3(b)所示,从左至右分别为一级至五级。
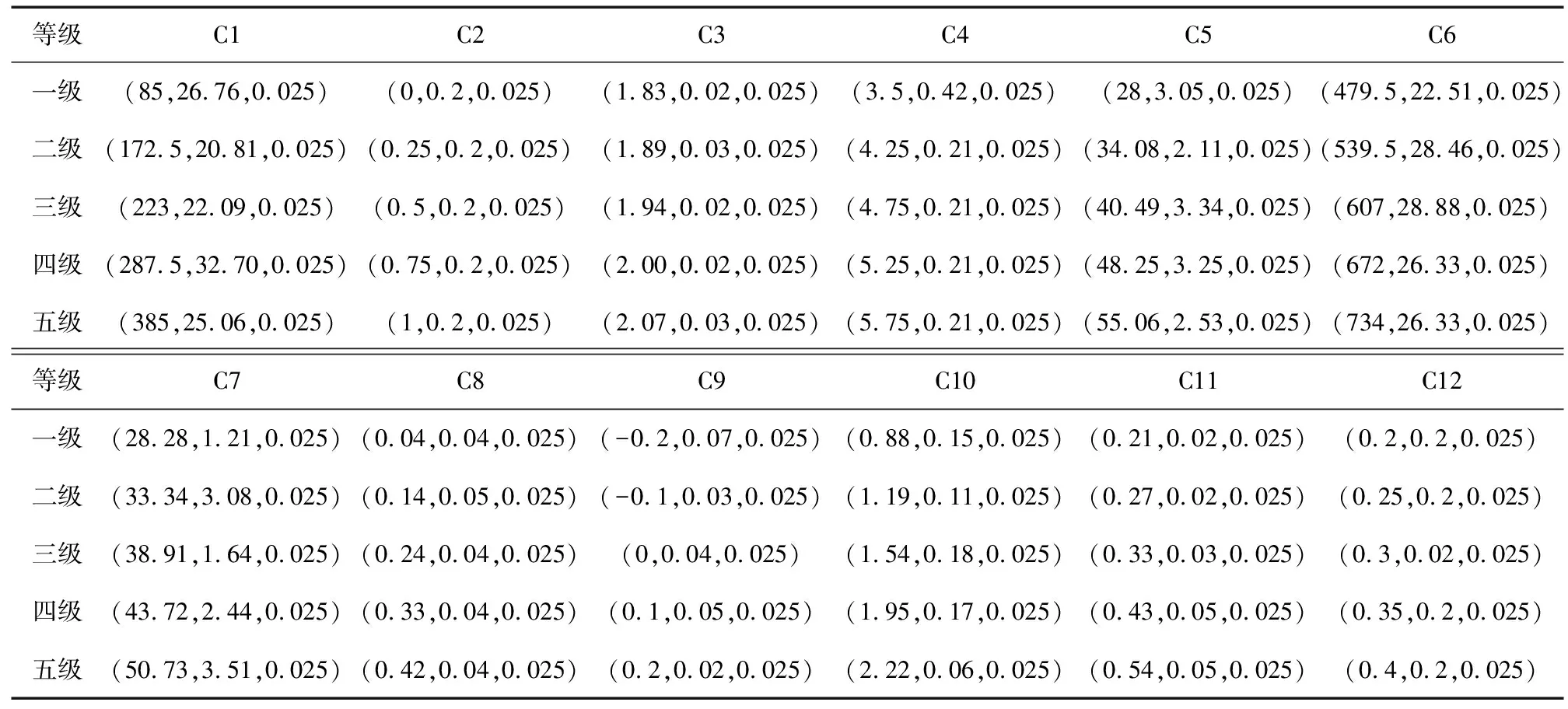
表5 评价指标数字特征Table 5 Numerical characteristics of evaluation indicators
研究区降雨多集中于夏季,约占年全年降雨量的69%,随着降雨量的积累,雨水不断渗入岩体,造成坡体表面冲刷,使得侵蚀、抗剪强度变差,进而发生滑坡。所选滑坡点降雨数据为100~385 mm,由图3(a)可知,四级时降雨云模型的熵相较于其他等级云模型的值稍大,故该滑坡点的降雨量可判别为四级。在图3(b)中,由于该滑坡区域地层岩性几乎不会发生变化,生成云模型前进行数据清洗,以方便后续综合评价云参数的计算,故地层岩性云模型中各等级分布均匀,无实际意义。

图3 评价指标云模型Fig.3 Cloud model for evaluation indicators
4.2 确定评价指标组合权重
为了更准确地衡量各评价指标间的关系,选取263条滑坡数据,根据式(7)~式(18),计算评价指标的基础权重,再由式(4)计算最优权重,各评价指标的权重如表6所示。
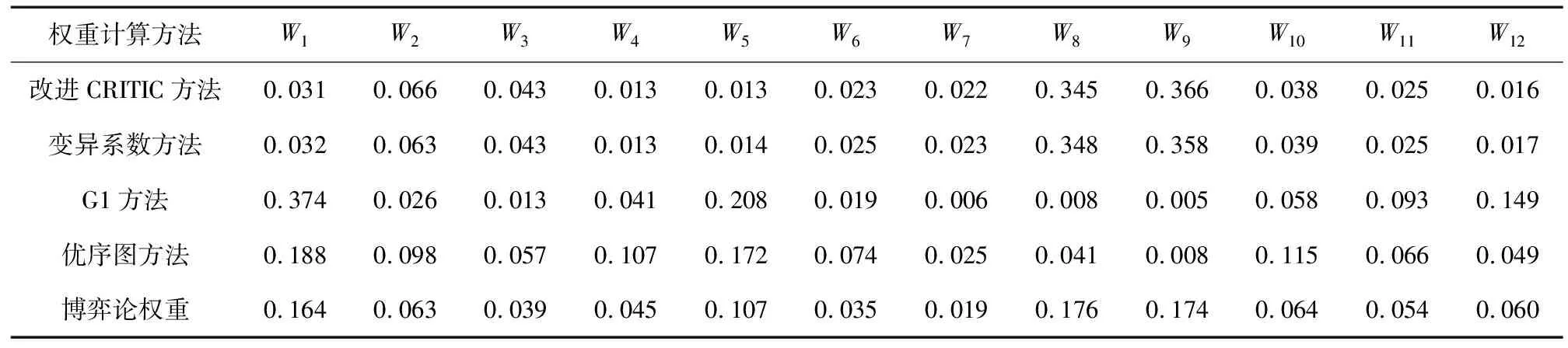
表6 评价指标的权重Table 6 Weight of evaluation indicators
4.3 确定综合评价云
计算出各评价指标的云模型特征参数后,再由式(19)计算出综合评价云参数,计算结果如表7所示,归一化处理后由Matlab生成综合评价云模型,如图4所示。

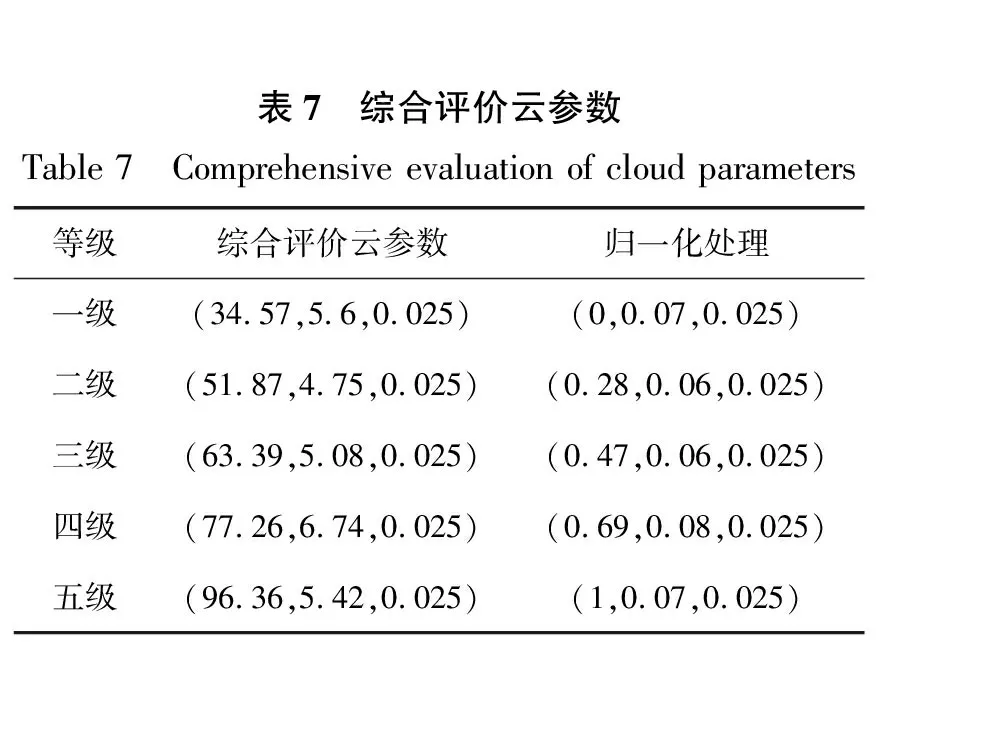
表7 综合评价云参数Table 7 Comprehensive evaluation of cloud parameters等级综合评价云参数归一化处理一级(34.57,5.6,0.025)(0,0.07,0.025)二级(51.87,4.75,0.025)(0.28,0.06,0.025)三级(63.39,5.08,0.025)(0.47,0.06,0.025)四级(77.26,6.74,0.025)(0.69,0.08,0.025)五级(96.36,5.42,0.025)(1,0.07,0.025)图4 综合评价云模型Fig.4 Comprehensive evaluation of cloud model
4.4 计算相似度
利用Matlab 软件根据定义计算出综合评价云模型与评价标准云模型的相似度结果δ1(δ1、δ2、δ3、δ4、δ5)为(0.63、0.58、0.55、0.70、0.62),然后计算出汉明距离δ2(δ1、δ2、δ3、δ4、δ5)为(4、4、5、1、3)。由此看出,两者计算的相似度最大的等级均为四级,即该滑坡的危险性等级为四级,与实际滑坡危险性等级一致。综合评价云模型(红色部分)与评价标准云模型(黑色部分)对比图如图5所示。由图可知, 二级和三级对应的云模型存在一定程度偏移,其原因在于危险性等级是由多个评价指标共同决定,即危险性等级为二级或三级时,部分评价指标的范围并不属于相应的等级范围。研究区的滑坡危险性分布如图6所示。

图5 相似度比较Fig.5 Comparison of similarity图6 研究区滑坡危险性分布图Fig.6 Landslide hazard distribution in the study area
4.5 对比验证
为了验证模型的有效性,引入模糊综合评判[23]和可拓物元模型[24]进行对比,对比结果如表8所示。由表8可知,云模型和模糊综合评判的预测结果均为四级,但模糊综合评判过程中需要对各评价指标进行打分,具有较强的主观性,而可拓物元模型准确性较差,且涉及大量计算,时间复杂度高。

表8 不同模型对比结果Table 8 Comparison results of different models
5 结论
引入博弈论和云模型的危险性评价方法,对铁路沿线上某一滑坡进行危险性评价,得出以下结论:
1)采用博弈论思想,求得基于改进CRITIC方法、变异系数方法、G1方法和优序图方法的最优权重,相较于其他方法提出的1种或者2种权重,更具科学性。滑坡危险性评价中涉及多种不确定性因素,引入云模型,克服了传统评价方法未解决定性与定量相结合的问题。较之其他方法,该方法时间复杂度低,所需参数少,评价结果更直观,可为滑坡危险性评价提供参考。
2) 以铁路沿线上某一滑坡为例,将综合评价云与评价标准云进行相似度对比,并采用汉明距离验证相似度对比结果,结果表明相似度对比结果基本一致,并与实际情况相符,该滑坡危险性等级为IV级(较高风险)。经实例验证,文中所提方法具有一定的实用价值。
3) 该方法仍存在一定的局限性,云滴由随机数生成,每次的评价结果略有不同,但不影响最终结果;模型的构建需要人为参与,存在一定的主观性,笔者下一步将探索机器学习方法在滑坡危险性评价中的应用。
