降雨作用下基于电导性能的土坡基质吸力时空变化试验研究
2024-03-13林昀昭简文彬陈瑞敏康浩隆章德生
林昀昭,简文彬,陈瑞敏,康浩隆,章德生
(1. 福州大学 岩土与地质工程系,福建 福州 350108; 2. 福州大学 福建省地质灾害重点实验室,福建 福州 350108)
0 引言
台风诱发的强降雨突发性强、影响范围广和成灾强度大,大量事实表明,降雨是影响边坡稳定性的主要因素,对降雨型滑坡发生、发展过程及滑坡灾害预警的深入研究具有重要的理论及现实意义。降雨入渗对滑坡稳定性影响中土体基质吸力的变化值得关注,随着雨水入渗,土体含水量增加,基质吸力减小,土粒间的摩擦力变小,使得边坡非饱和带土体的抗剪强度下降,进而导致边坡稳定性的降低[1-3]。基质吸力是非饱和土性质的一个重要表征,早期对基质吸力的影响因素研究归结于含水量或饱和度的变化。随着研究的深入,学者们发现压实度、温度、干密度、孔隙比、黏粒含量和含盐量等因素[4-7]也能在不同程度上对土体基质吸力产生影响。目前关于基质吸力对滑坡影响的探究多以现场监测与室内试验为主,人工降雨滑坡试验是研究降雨诱发滑坡致灾机理的重要手段,能够直观反映出滑坡不同空间位置各参量的变化规律。学者们开展了许多相关工作,进行了降雨与地下水位的耦合、坡面种以不同植被同时结合台风暴雨等工况下的滑坡室内物理模型试验,观测滑坡模型的渗流与位移[8-11]。这些试验多以含水率与位移为关注重点,对土壤电阻率指标关注较少,土壤电阻率大小和含水率、土颗粒直径与矿物成分、孔隙液体化学成分等有关,是土的重要物理性质。由于其测试方便、快捷和廉价,在边坡研究方面也得到了相关应用。国内外学者通过在边坡布设长期的电阻率测试装置、电阻率层析成像技术(electrical resistance tomography, ERT)等手段,建立了滑坡土壤水文特征与电阻率特征间的关系[12-13]。显然,电阻率对水分具有较高的敏感性,对于水分分布特征、运移规律复杂多变的天然边坡,利用岩土体电阻率来反映其含水率分布及变化规律具有一定的可行性,但目前对相关方面的研究仍比较少见。
本文将电阻率作为监测量与常规的含水率、基质吸力相结合进行人工降雨室内滑坡物理模型试验,并在边坡模型上种植马尼拉草,基于电导性能探究非饱和残积土边坡模型在不同降雨模式下的渗流特征与基质吸力时空变化。研究成果对进一步揭示降雨条件下滑坡基质吸力变化规律与电导演化规律,对降雨型滑坡预警具有理论及实际意义。
1 非饱和残积土边坡模型试验
1.1 试验土体
试验所用的土体取自福州市闽侯县溪源宫边坡露头,为花岗岩残积土,土体相关物理力学性质参数如表1 所示。试验所用土方量约为1.5 m3,由于试验所需土方量较大,在现场由勾机从坡面挖下土体并装车中采回。土体取回后,存在小碎石与植物根系等杂质,因此采用5 mm×5 mm的筛网进行过筛,筛除杂质。而后将土体放入轻型搅拌机,并用电动喷雾器将水分均匀喷洒至土体,配置到所需含水率。

表1 岩土物理力学性质参数Table 1 Physical and mechanical properties of rock-soil
1.2 试验装置
模型箱为固定式钢槽,为尽量减小尺度效应影响,选择长×宽×高为3m×1.5m×1.5m,模型箱两侧使用厚度15mm的钢化玻璃。降雨系统由控制模块、动力模块和管路模块三大部分组成,有效降雨面积为3m×4m,降雨高度为5m。降雨强度的变化范围10~150 mm/h,调节精度7mm/h左右,可满足试验降雨方案要求。边坡模型坡体含水率、电阻率的监测使用Acclima 公司的TDR-310H传感器(2019年推出)进行采集,含水率测量范围0~100%,分辨率0.1%;电导率测量范围0~5000 μS/cm,分辨率0.1 μS/cm,经换算后变为土壤电阻率(土壤电导率与电阻率数值上互为倒数)。TDR-310H是一个集成的时域反射计,具有较好的稳定性;基质吸力的采集选用WATERMARK 200SS型多孔介质土壤湿度传感器,基质吸力测量范围0~199kPa,分辨率0.1kPa。传感器由封装在颗粒基质内的耐腐蚀电极组成,通过固态电阻感应装置测量土壤基质吸力。数据采集系统使用CR1000数据采集器和配套的LoggerNet软件,实时观察与保存试验过程中各监测元件数据。降雨设备与土体监测原件如图1所示。

图1 降雨设备与土体监测原件Fig.1 Main equipments of rainfall simulations and soil monitoring sensors
1.3 边坡模型堆置与监测元件布置
由于福建地区滑坡多介于25°~35°,因此模型边坡坡度选择30°。坡顶土层厚度为55cm,传感器布置于坡顶浅层(埋深15cm)、坡顶中层(30cm)、坡顶深层(45cm)、坡中浅层(15cm)、坡中中层(30cm)、坡中深层(45cm)、坡底浅层(15cm)、坡底深层(30cm),对土体电阻率、含水率和基质吸力进行采集。模型土坡分多层进行堆置夯实,每层厚度约为10 cm。堆置过程中首先计算好每层体积与所需土体重量,并在堆坡前称量完毕,采用定制木板固定每层位置,用铁锤对各部位均匀逐次进行敲击,夯实完毕后,及时用环刀取样对模型土坡的密度进行测定。土坡模型土体含水率与密度的配置均为人工配置,含水率配置区间控制为20%~26%,土体密度的配置区间控制为1.4~1.6 g/cm3。监测元件在土坡堆置时一并埋入预定深度,如图2所示,图中W表示电阻率含水率传感器,J表示基质吸力传感器,3表示坡顶,2表示坡中, 1表示坡底。例:J3-15表示坡顶埋深15 cm处基质吸力传感器。
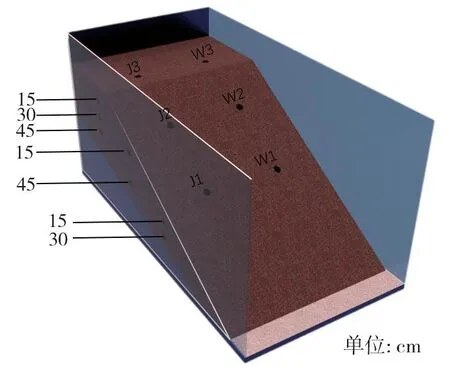
图2 模型边坡监测件埋设示意图Fig.2 Schematic diagram of slope monitoring embedding
1.4 护坡草的种植
为了研究草本植物对边坡入渗的影响,同时结合试验场地、时间等客观因素的影响,所选护坡植被必须同时具备以下几个特点:①草本植物生长适应性足够强,对土壤要求不能过高,在持续高温、降雨情况下可正常生长;②生长速度快,有效覆盖率高;③根系足够密集,吸收、传导水分能力强。综合以上几个特点,同时结合福建地区常见护坡植被类型,选取长势好、无病虫害的马尼拉草皮约6 m2运回试验场进行种植并养护30 d后进行试验。马尼拉草为多年生草本植物,颜色呈青绿色,具横走根茎,叶片在结缕草中属半细叶型,长3~4cm,宽1.5~2.5mm,叶质硬,扁平或内卷。具备良好的抗旱性、抗热性、耐阴性和耐践踏且生长快,因此,被广泛用于固土护坡。完工后模型边坡如图3所示。

图3 模型边坡Fig.3 Model slope
1.5 降雨方案
本次降雨模拟根据福建地区降雨特点[14],共进行3组试验,6次降雨,各组试验方案如表2所示。试验1探究裸坡在均匀降雨下的入渗特征,试验2和试验3为植草边坡在均匀降雨(3 h降雨均为恒定雨强)、前小后峰(3 h降雨中前1.5 h雨强为20 mm/h,后1.5 h雨强变为60 mm/h)、前峰后小(前1.5 h雨强为60 mm/h,后1.5 h雨强变为20 mm/h)3种暴雨模式下的入渗特征,每组试验进行2次降雨。
2 试验结果与分析
2.1 累次降雨下边坡模型含水率变化分析
边坡模型在不同降雨条件下各部分土体体积含水率时变曲线如图4所示,雨强情况标注于图中灰色参照线之间,具体雨强与历时等如表2所示。共进行4次降雨,每次试验完毕将模型边坡放置一周进行退湿,直至含水率与试验前相近。值得注意的是,文中试验数据的采集频率为5 min,所用CR1000数据采集器和与其配套的LoggerNet自动采集软件能将5 min内所采集的所有数据进行平均,以此作为输出值,因此,文中含水率数据会出现精确到0.01%的现象,所测得的含水率为体积含水率。
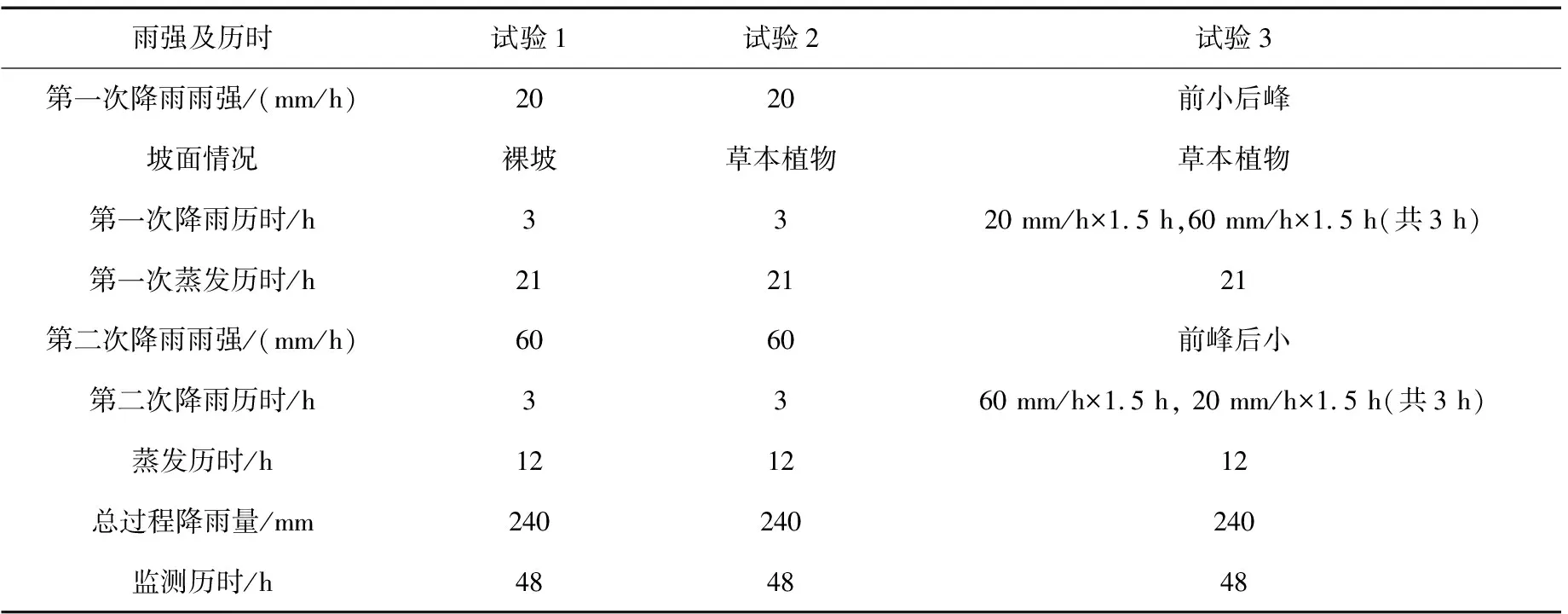
表2 人工降雨试验方案Table 2 Artificial rainfall test scheme
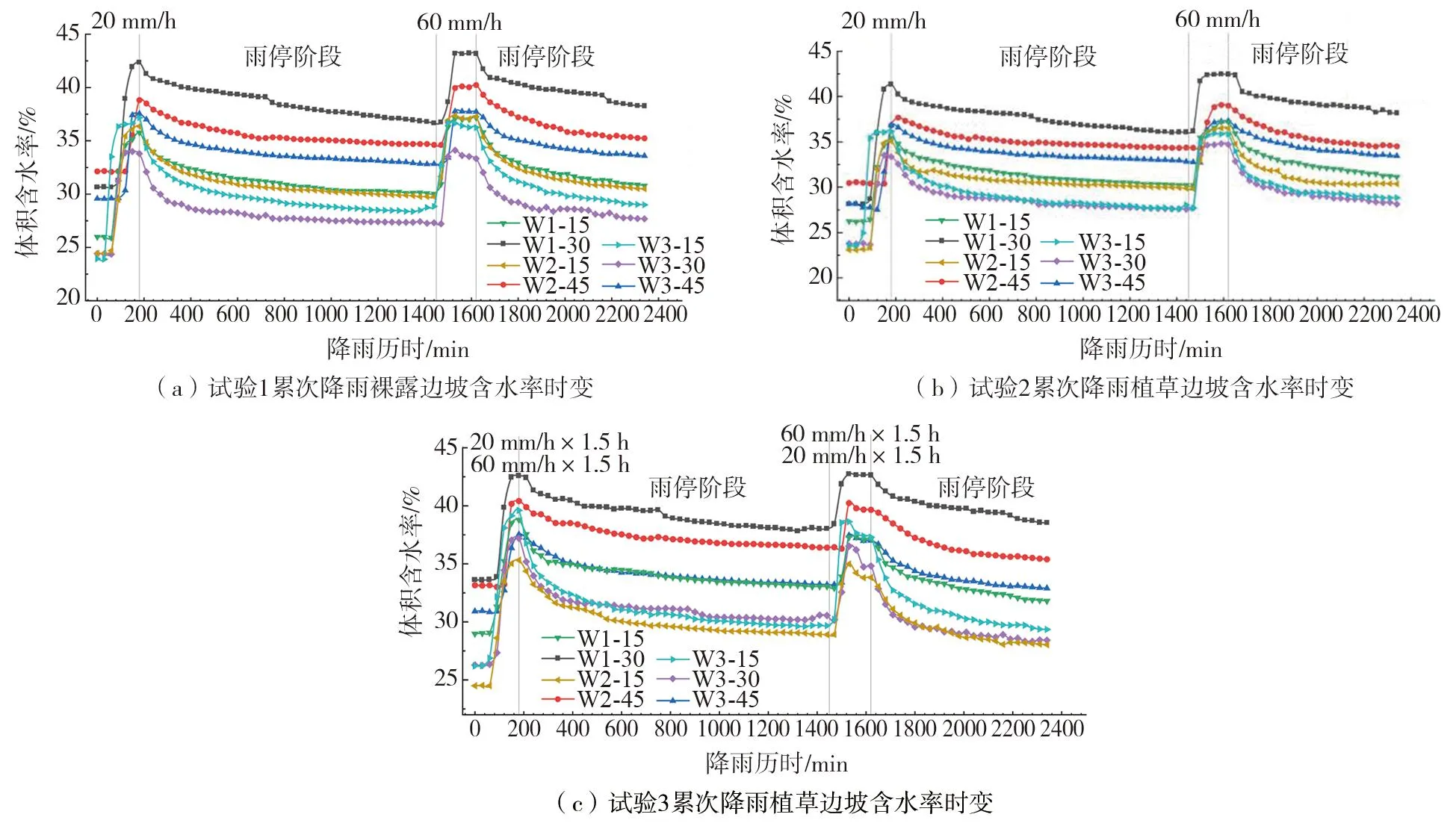
图4 累次降雨模型边坡含水率时变图Fig.4 Time varying curves of soil model slope moisture content under repeated rainfall
2.1.1 降雨作用下边坡模型含水率变化规律
由于室内边坡模型堆建过程有时间差以及建成后存在水分蒸发,边坡各深度处土体初始含水率存在差异,表层土体初始含水率稍低于深层土体。降雨开始60~90min后,边坡表层土体传感器率先开始响应,含水率迅速上升,上升速率与增加幅度均大于坡体内部土体,降雨初期表层土体含水率时变曲线斜率陡于深层土体。相较于坡中与坡底,坡顶表层传感器W3-15最先开始响应,这是由于W3-15所处坡顶为平缓地面,水分能够垂直入渗,而坡中与坡底传感器由于一部分水分顺着坡面倾角形成径流流走,因此入渗水分较少,响应较慢。随着降雨持续进行,水分入渗由边坡表层逐渐向深处发展,深层土体由于饱和度较高,渗透路径长,因此雨水要经过相对较长的时间才能渗透到坡体深处。
在含水率变化方面,坡脚深部土体含水率峰值与变化幅度最大,以试验2第一次降雨为例,在3 h降雨下W1-30含水率由28.14%变为41.33%,上升了13.19%。这是由于在降雨过程中坡脚深部土体除受上方雨水入渗外,坡中、坡顶处土体部分水体在重力作用下,也会顺着边坡倾角往坡脚方向流动,汇集到坡脚深处。未渗入边坡的雨水沿坡面表层向坡脚流动,汇集在坡脚,渗入坡脚内部,造成坡脚深部土体含水率增大。累次降雨中,第二次降雨时坡体上部吸水能力变弱,含水率增加幅度降低,2次降雨结束后边坡表层土体含水率值相差较小(试验2中W3-15第一次降雨含水率峰值为36.17%,第二次结束为36.03%)。深部土体在雨停期间上部土体水分的下渗及蒸发作用较弱,在第一次降雨的残余含水量与第二次降雨的持续入渗下,含水率峰值提高较明显(试验2中W2-45第一次降雨结束含水率峰值为37.80%,第二次结束为39.07%)。降雨停止后,边坡表层土体含水率随即开始下降,深层土体因雨停后表层水体持续下渗,含水率稳定一段时间后开始下降。在退湿过程中,表层土体受到蒸发作用较强,土体水分不断蒸发,含水率逐渐下降。深层土体蒸发作用较不明显,含水率在退湿过程中下降较少,一定时间内,蒸发作用对土体影响深度有限。
试验1和试验2降雨模式一致,均为固定雨强的均匀降雨,在同样降雨强度、历时下,相比于裸露边坡,植草边坡各部位的降雨响应时间略迟于裸坡,试验1和试验2第一次降雨传感器响应时间如表3所示。以坡脚处埋深15 cm的点W1-15为例,第一次降雨结束后,试验1裸露边坡W1-15的含水率为37.77%,试验2植草边坡W1-15处的含水率为35.42%,降雨后植草边坡土体含水率低于裸坡。这是由于边坡模型草皮种植密度大、覆盖率高,茂盛的草本植物叶片对边坡表面形成多层遮挡,导致部分降水存留在植物上,未能参与地表入渗与径流形成,产生截留作用,减少雨水向边坡内部的有效入渗量。尽管降雨时雨水顺着草本植物根系入渗,容易产生优先流加快水分下渗,但本次试验中马尼拉草根长有限(4~6 cm),且模型边坡坡度为 30°,平行坡面方向的渗流较强,对优先流的产生与流动产生了一定程度抑制作用,导致植草边坡入渗速度慢于裸坡。降雨结束后在褪湿过程中,植草边坡在21 h雨停时间内含水率下降值低于裸坡,这是由于草本植物具有持水能力,在降雨结束的一段时间内能够有效地减少水分蒸发作用,因而起到水土保持的作用。

表3 传感器响应时间表Table 3 Sensor response schedule
2.1.2 不同降雨模式下模型边坡含水率变化规律
试验2和试验3植草边坡降雨量与降雨总历时一致,降雨强度与变化不同。试验3为20mm/h与60mm/h这2种雨强交替下前小后峰、前锋后小的动态降雨模式,试验2则为雨强恒定的均匀降雨。对比试验2和试验3,以坡脚处埋深15cm的点W1-15为例,均匀降雨情况下,观察图4(b)W1-15处土体降雨期间含水率一直呈现上升态势。动态变化雨况下,边坡表层土体的变化趋势会随降雨强度变化做出响应,以试验3第二次降雨为例,降雨强度由60mm/h变为20mm/h时,观察图4(c)W1-15处土体含水率出现一定程度下降,该现象不是降雨强度变小后立刻发生的,而是出现一定时间延迟,表层土体响应较明显,植草边坡降雨入渗存在一定滞后性。
2.2 累次降雨下边坡模型电导性能演化规律分析
边坡模型在不同降雨条件下各部分土体电阻率时变曲线如图5所示。
2.2.1 降雨下植草边坡模型电导性能演化规律
由图5可知,植草边坡坡体初始电阻率值分布较为离散,具体表现为表层坡体电阻率较大,随深度增加电阻率逐渐下降,试验2中坡顶处不同深度电阻率初始值分布分别为W3-15(343.03 Ω·m)、W3-30(262.56 Ω·m)、W3-45(238.89 Ω·m)。草本植物改变了边坡土体的蒸腾作用,边坡深部土体水分蒸发更为困难,不同深度处水分差异更明显。降雨60 min后,边坡浅层土体快速响应,电阻率显著减小,响应后50~90 min达到最低值并保持稳定。试验2中W3-15在降雨60 min后开始响应,降雨第140 min时,电阻率从315.19 Ω·m降为152.86 Ω·m,降幅达到了162.33 Ω·m。降雨过程中,边坡表层土体电阻率受降雨强度影响明显,降雨强度越大,电阻率降低速率与幅度越大。第二次降雨后,边坡各部分电阻率最低值均比第一次降雨更小,坡体导电性能增强。
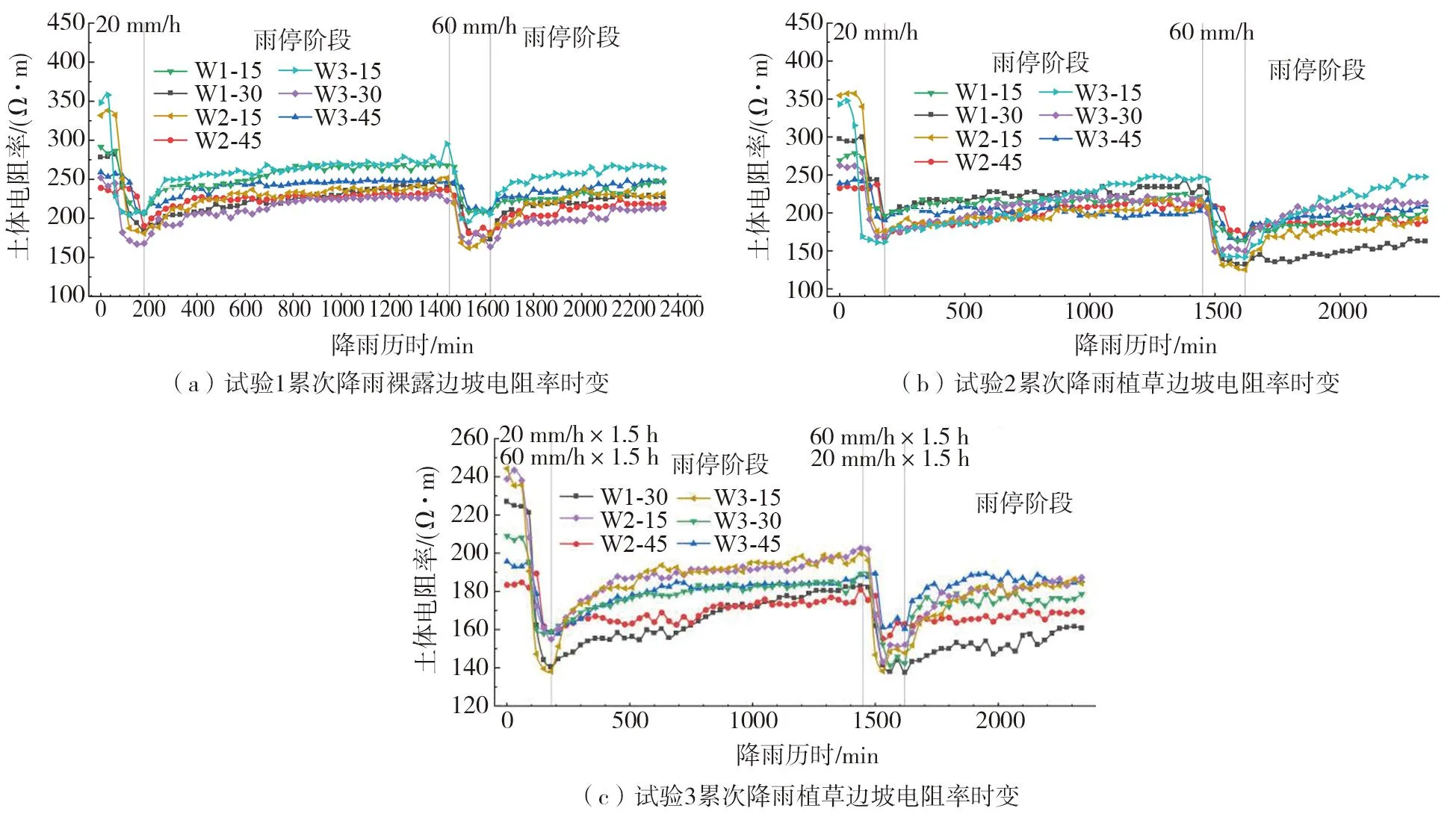
图5 累次降雨模型边坡电阻率时变图Fig.5 Time varying curves of soil model slope resistivity under repeated rainfall
对比边坡含水率与电阻率响应时间,发现两者几乎同时响应,但含水率呈增长趋势,电阻率则呈降低趋势。随着含水率增加,土体电导性能加强,土体含水率达到峰值时,电阻率最小。究其原因,由于水分下渗,土体孔隙水含量升高,使得土体导电路径增加。土体水分极低时,土体导电主要依靠紧密接触的土颗粒与少量的土水相串路径导电;水分开始入渗后,土水相串导电路径增加,孔隙水间的水路导电初步形成;随着入渗水分增加,孔隙水之间得到连通,水路导电能力增强,形成土颗粒传播、孔隙水传播和土水相串传播三路并联的导电路径,土体电阻率明显减小。在水分分布复杂的边坡中,电阻率无论是从响应时间还是变化幅度方面,都能很好地反馈水分赋存状态。
同等雨强下,相比于裸露边坡,植草边坡各部电阻率响应时间略迟于裸坡,这是由于土体电阻率大小与水分变化关系密切。试验2由于植被的截留作用导致水分入渗较慢,进而导致植草边坡电阻率响应较迟,试验1和试验2第一次电阻率传感器响应时间如表3所示。降雨结束后,裸露边坡电阻率降低幅度大于草皮边坡,这是由于边坡模型上的草本植物影响了水分的下渗,雨水有效入渗量减小,进而影响电阻率的降低幅度。
2.2.2 不同降雨模式下模型边坡电阻率变化规律
对比图5(a)、(b),在总降雨量一致的情况下不同降雨模式边坡土体电阻率变化趋势产生了差异。试验2均匀降雨情况下边坡土体在降雨期间电阻率呈现先下降后趋于稳定的态势,观察试验3第二次降雨,在前小后峰的动态降雨下,边坡土体降雨过程中出现下降后发生小幅回升的情况,对雨强由60mm/h变为20mm/h做出响应。无论是电阻率还是含水率,均能对动态降雨做出响应,但都存在一定的滞后性。
2.3 累次降雨下边坡模型基质吸力变化
试验1、试验2和试验3第一次降雨模型边坡各部分基质吸力时变图如图6所示。
非饱和土体基质吸力能够将土颗粒聚在一起,增加土体抗剪强度。降雨期间入渗到边坡内的雨水会使土的吸力降低,进而影响土体抗剪强度,不利于边坡稳定。在边坡模型的制作过程中,各部分的初始基质吸力因制做过程中温湿度等外部因素影响,导致边坡表层基质吸力大于坡体内部。试验3中边坡模型坡顶埋深15、30、45cm处的初始基质吸力分别为37.8、36.2、30.6kPa。由图6可知,土体吸力响应时间基本同步于含水率。2次试验均是表层土体基质吸力最早开始发生变化,深部土体基质吸力响应时间较慢,与土体含水率变化规律一致。试验2在相同雨强下,由于草皮边坡水分入渗略缓于裸坡,因此基质吸力的响应时间慢于试验1。

图6 模型边坡基质吸力时变图Fig.6 Time varying plot of matrix suction of the model slope
试验2和试验3植草边坡降雨量与降雨总历时一致,降雨强度与变化不同。试验3为20mm/h与60mm/h这2种雨强交替下前小后峰、前锋后小的动态降雨模式,试验2则为雨强恒定的均匀降雨。降雨过程中,试验2和试验3土体吸力虽然响应时间不同,但变化趋势相似,均是在降雨一段时间后,边坡表层土体吸力开始响应并在较短间内迅速降低,深层土体吸力响应时间较慢,且变化速率也较表层小。不同降雨模式下土体基质吸力虽然响应时间不同,但变化趋势相似。这是由于随着水分的入渗,土水特征曲线进入毛细作用段,土孔隙水主要以毛细水的形式存在,土中大孔隙的水分开始向外流失,土体基质吸力已经大幅下跌,此时尽管雨强发生变化,但土体基质吸力已大幅下跌,在短时间内难以回升,雨强的变化难以对其造成较大波动。
3 土坡基质吸力时空分布与计算
3.1 土坡基质吸力及电阻率时空分布
根据已测得数据,使用克里金插值法绘制边坡模型在试验2第一次降雨开始前、降雨120min、降雨结束20min后(即240min)基质吸力与电阻率分布剖面图,如图7和图8所示。
由图7可知,降雨前边坡表层土体基质吸力较高,随着深度增加基质吸力慢慢递减,最深部土体基质吸力值在整个边坡中最小,并且坡顶、坡中的表面土体基质吸力略高于坡脚表面土体。这是由于表层土体蒸发作用较为强烈,且水分在重力势作用下会向深部与边坡倾角方向运移,当土体孔隙中的水分增加时,基质吸力相应减少。降雨120min后,表层土体基质吸力消失殆尽,深部土体由于水分还未充分入渗,因此基质吸力值仍然较大。在整体分布上呈现边坡表层基质吸力趋近于零,随着深度增加值逐渐增大,且跛脚处基质吸力较小。这是由于跛脚处土体在降雨过程中不仅受上方雨水入渗,坡中坡顶处土体部分水分在重力作用下,也会顺着边坡倾角往坡脚方向汇集,水分入渗更充分,因此基质吸力较小。降雨结束20min后,水分入渗较为充分,此时深部土体基质吸力下降明显,整体分布呈现上部与坡脚基质吸力较小,深部基质吸力稍大,但总体上各部位基质吸力值有限。

图7 模型边坡基质吸力分布剖面图Fig.7 Profile of matrix suction distribution of the model slope
由图8可知,降雨前边坡模型表层电阻率最大,随着土体深度增加而逐渐减小,并且坡顶、坡中深部土体电阻率在整个边坡模型中最小。降雨120min后,由于水分入渗,边坡表层土体电阻率下降明显,中层土体出现一定程度跌幅,深层土体由于水分未充分下渗,因此电阻率在整个边坡中最大。降雨结束20min后,水分入渗较为充分,深部土体电阻率值也受到影响,土体电阻率在边坡上的分布表现为由浅层到深层逐渐加大,但整体上边坡各处电阻率相差值有限。
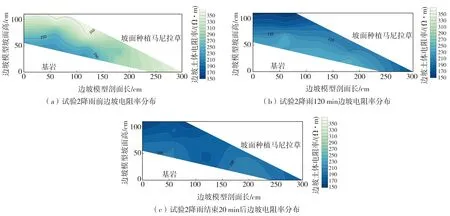
图8 模型边坡电阻率分布剖面图Fig.8 Resistivity distribution profile of model slope
3.2 基于电导性能的残积土基质吸力计算模型
基质吸力能够作为土体黏聚力的组成部分提高土体抗剪强度,增强边坡稳定性[1]。基质吸力具有极强的水敏性(由土水特征曲线可知),随着含水量增加其值迅速下降。大多数自然边坡均处在非饱和状态(或局部饱和),因此降雨后随着水分入渗,土体基质吸力迅速下降,黏聚力减小,导致边坡的稳定性下降。在滑坡预警中,基质吸力作为重要监测指标,其大范围监测手段仍不够多样、便捷。对比图7和图8,边坡电阻率与基质吸力在整体分布上具有一定相似性,同种性质非饱和土电阻率大小主要取决于含水率的变化,基质吸力大小亦是如此,非饱和土电阻率与基质吸力之间必然存在一定内在联系[15-17]。因此,可通过对土体电阻率相关指标的测量进而计算基质吸力大小,达到简化非饱和土吸力测试的目的。并且得益于电阻率更为多样与便捷的检测手段(如电阻率成像法(ERT)等[13,15]),用电阻率来间接测量基质吸力不失为一种更加便捷有效的方法。
3.2.1 残积土电阻率-含水率关系
ARCHIE[18]于1942年提出适用于饱和无黏性土的电阻率结构模型,建立饱和无黏性土电阻率ρ随孔隙水电阻率ρw的变化关系式为
ρ=aρwn-m
(1)
式中:ρ为土体电阻率(kPa);ρw为孔隙水电阻率(°);a为土性参数;m为土性参数;n为孔隙率。
由于ARCHIE公式是最简化的电阻率模型,适用范围有限,因此,许多学者将饱和度指数、温度和结构性参数等[19-21]引入修正或建立新的电阻率模型,如KELLER等[19]将ARCHIE模型拓展于非饱和土并建立了新的方程:
计算完近似的头长度和尾长度之后,再按式(5)计算近似的最大完工时间。在求解JSP著名的N6[4]、N7[5]邻域结构中,均采用了该评价方法。值得注意的是,在JSP的N6、N7邻域结构中,工序u和v以及之间的工序组成的序列Q={u,l1,l2,,lk,v}均为关键工序。本文同机器移动工序时,使关键工序移动范围突破了工序块的内部、紧前、紧后位置限制,因此,序列Q={u,l1,l2,,lk,v}不一定均为关键工序,进一步扩展了Balas所提出的近似评价方法的应用范围。
(2)
式中:Sr为饱和度;p为饱和度指数。
土的体积含水率与土的饱和度密具体转换关系为
(3)
式中:θ为体积含水率;VW为孔隙水体积;V为土样总体积;w为含水率;γd为土的干重度;γW为孔隙水重度;n为土体孔隙率。
联立式(2)与式(3)得土体电阻率-体积含水率关系式为
ρ=aρwnp-mθ-p
(4)
3.2.2 残积土含水率-基质吸力关系
非饱和土中,土体吸力与体积含水率之间的关系曲线称为土-水特征曲线(SWCC),土-水特征曲线与土的渗透函数、抗剪强度指标[21-22]等有关。常见的模型有Van Genuchten(VG) 模型、Fredlund-Xing模型等,VG模型表达式为[23]
(5)
式中:θs和θr分别为饱和体积含水率与残余体积含水率;ψ为吸力;α、β为拟合参数。
由于残积土残余含水率较难测定,因此,有学者不考虑残余含水率[24]的影响,对VG模型进行修正:
(6)
3.2.3 残积土电阻率-基质吸力预测模型
结合VG模型参数中的体积含水率-基质吸力关系与KELLER修正模型中的电阻率-体积含水率关系,根据式(4)与式(6),可得基质吸力-电阻率的数学模型表达式为
(7)
式中ρs为饱和土体电阻率。
将试验所测得的参数代入式(7)拟合,可得α=0.03、β=1.63、p=1.46,基于土体电阻率的残积土基质吸力计算模型为:ψ=33.33[(ρ/ρs)1.77-1]0.6,R2=0.84,拟合关系曲线如图9所示。在测得数据中随机抽取部分点,代入拟合公式验算,将实测值与拟合值进行比较,误差范围较为合理,如表4所示。在实际工程应用中的基质吸力的现场测试较为不方便,可以通过测试非饱和残积土的电阻率大小,使用式(7)计算非饱和土的基质吸力大小,并且后续也可结合ERT等技术,通过不同学科整合,为后续的防灾减灾工作提供一定的帮助[25]。
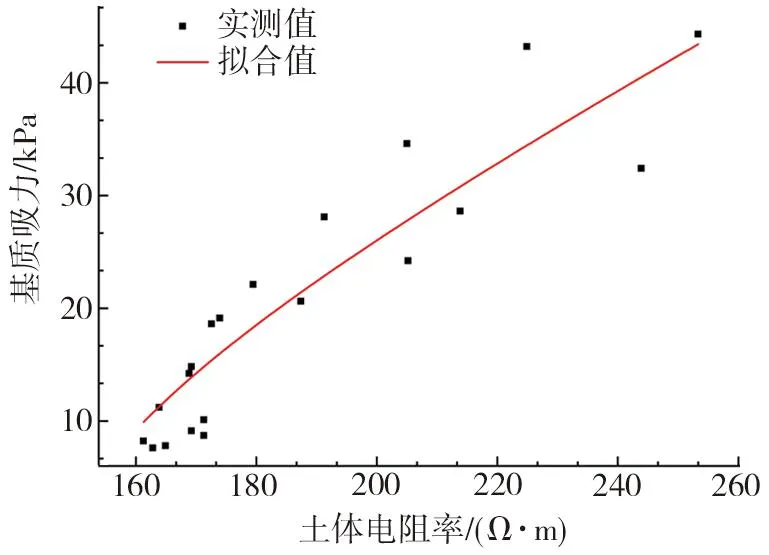
图9 残积土电阻率与基质吸力关系拟合曲线Fig.9 Fitting curve of residual soil resistivity and substrate suction

表4 电阻率-基质吸力预测模型计算结果Table 4 Calculation results of resistivity-matrix suction prediction model
4 结论
本文通过人工降雨室内边坡模型试验,将电阻率作为监测量与常规的含水率、基质吸力相结合,探究残积土边坡在累次降雨作用下的渗流特征与电导性能变化,得到以下结论:
1)马尼拉草由于茂盛叶片对雨水的截留作用及根系长度较短优势流有限,不利于雨水入渗。在相同雨强下马尼拉草边坡响应时间较慢,电阻率、含水率和基质吸力变化量均小于裸坡。
2)模型边坡含水率与电阻率传感器几乎同时响应,随着含水率的增加,土体的电导性能加强,当土体含水率达到峰值时,电阻率最小。在前小后峰、前峰后小的动态降雨模式下,无论是电阻率、含水率,均能对动态降雨做出响应,但都存在一定的滞后性。
3)结合KELLER改进的ARCHIE拓展模型与VG模型,得到基于电阻率的残积土基质吸力计算模型,为非饱和残积土基质吸力的测量提供一种快速便捷的方法。
