核电循环泵行星齿轮热弹流润滑研究
2024-03-13董庆兵汪汉明冯成程魏静何东杨海师
董庆兵,汪汉明,冯成程,魏静,何东,杨海师
(1.重庆大学机械传动国家重点实验室,重庆 400044;2.重庆大学机械与运载工程学院, 重庆 400044;3.重庆齿轮箱有限责任公司,重庆 402263 )
核电循环水泵是沿海核电站重要设备,其作用是向汽轮机的凝汽器和辅助冷却水系统提供冷却水,降低核反应堆运行温度,避免高温熔毁核反应装备,其可靠性直接影响到核电机组的安全运行。核电齿轮箱的良好润滑性能是核电循环泵可靠运行的重要保障,而润滑不良会给核电机组带来巨大的经济损伤和安全隐患。据不完全统计,因润滑不良导致的设备事故约占25%,与润滑因素相关的设备故障高达40%[1]。因此,研究提升核电齿轮箱的润滑性能具有重要意义。然而,如何减小齿面润滑不良造成的接触疲劳,仍是当前提升核电齿轮箱服役性能关注的热点问题。
齿面润滑是集热-固-流等多个物理场的典型弹流问题,国内外学者对齿轮的热弹流润滑问题已展开了广泛研究。早期渐开线齿轮啮合中的弹性流体动力润滑(EHL)研究模型大多集中在直齿轮,且假设接触表面光滑的情况[2-4]。随着齿轮精度和平稳性要求的逐渐提高,斜齿轮的应用更加广泛,且粗糙表面对齿轮弹流润滑的影响已不容忽视。斜齿轮在啮合过程中啮合线长度时刻变化,摩擦力沿着接触线方向也不统一,相较于直齿轮的啮合特性和润滑性能更复杂多变。莫云辉和巢桐[5]提出有限宽线接触正反圆锥滚子模型作为斜齿圆柱齿轮的等效模型。杨萍和杨沛然[6]研究了斜齿圆柱齿轮瞬时的准稳态热弹流润滑行为,分析了端部修形对润滑参数的影响。CLARKE等[7]根据斜齿轮啮合瞬态弹流润滑数值结果,分析了轮廓误差对斜齿轮润滑性能的影响。YANG等[8]考虑真实三维粗糙表面,分析了斜齿轮啮合过程中的混合EHL特性、摩擦力和闪温。上述研究考虑了齿轮修形、粗糙表面等特性对其外啮合斜齿轮弹流润滑结果的影响,但综合因素下内/外啮合的弹流润滑行为有待深入研究。
本文作者以核电循环泵人字齿行星传动系统为研究对象,忽略平行斜齿轮相互的轴向作用,考虑齿廓修形造成的啮合误差,以及齿面磨合期形貌的塑性变形等因素,利用移动平均滤波方法对未经磨合的初始形貌进行光滑处理,建立了典型工况下核电循环泵行星传动系统斜齿轮热弹流润滑模型,研究了内/外啮合齿轮副接触区域内油膜厚度、油膜压力、摩擦应力、闪温等润滑参数的变化规律,分析了齿面形貌和齿廓修形对其润滑行为的影响,为核电循环泵齿轮箱的运行可靠性和接触性能优化提供了技术手段和理论基础。
1 行星齿轮三维结构及齿面接触分析
1.1 行星轮系结构参数
核电齿轮箱通常采用立式NGW结构、功率四分流人字齿行星轮系一级传动,如图1所示,由于行星轮系的人字齿为对称结构,因此对单侧斜齿轮进行弹流润滑计算。

图1 核电循环泵齿轮箱三维结构Fig.1 Three dimensional structure of gear box of nuclear power circulating pump
齿轮的主要参数如表1所示,其中齿宽表示人字齿两侧齿宽及中间轴长度之和。
由于装配误差、制造误差及齿轮受载后弹性变形等因素的影响,齿轮啮合过程中会出现偏载和啮合冲击,工程应用中主要采用齿廓修形来减小啮合冲击和应力集中。
文中针对核电循环泵齿轮采取齿顶线性修形,其端面示意图如图2所示。图中:Ca表示最大修形量,La表示修形长度。线性修形指的是在齿轮啮合线上,任意修形位置x与修形量Δ之间呈线性关系,具体公式如式(1)所示。考虑实际加工难度、经济成本等因素,一般只对太阳轮或行星轮进行修形。文中按照表2所示参数对太阳轮和行星轮进行齿顶线性修形,在Fortran程序中可更改这些修形参数,从而求解不同修形量下弹流润滑数值结果。

图2 齿顶修形端面示意Fig.2 Schematic of tooth tip modification end face

表2 行星齿轮齿顶修形参数Tab.2 Planetary gear tooth tip modification parameters
Δ=Ca(x/La)
(1)
1.2 行星齿轮内/外啮合齿面接触分析
斜齿轮齿面接触线的长度在啮合过程中是时刻变化的,考虑齿轮重合度的影响,实际斜齿轮在啮合时同时存在多条时变接触线。文中模型在齿轮啮合3/4齿交替的齿面上每条啮合线都具有时变性。文中采用切片法,将斜齿轮沿齿宽方向划分成若干份斜齿轮薄片,对单个齿轮薄片的刚度进行累加,从而得到斜齿轮副的啮合刚度。实际传动中轮齿啮合刚度受到多种因素影响,文中考虑斜齿轮接触变形、齿廓偏差、轮体变形以及轴向力的影响,得到轮齿误差影响下的多齿综合啮合刚度表达式[9]如下:
(2)
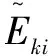
基于上述综合啮合刚度可推导出齿轮薄片j的载荷分配系数表达式为
(3)
斜齿轮啮合副的瞬时啮合状态热弹流润滑问题可以近似等效为圆锥滚子的准稳态热弹流润滑问题,如图3所示。内啮合副可等效为两同向的圆锥滚子内切接触问题,即内啮合线上某点与齿圈基圆相切的曲率半径对应半径R1,与行星轮基圆相切的曲率半径对应半径R2。外啮合副可等效为两反向的圆锥滚子外切接触问题,即外啮合线上某点与太阳轮基圆相切的曲率半径对应半径R3,与行星轮基圆相切的曲率半径对应半径R4。
由图3可得行星轮与内齿圈的曲率半径R1、R2表达式为

图3 行星轮内/外啮合等效示意Fig.3 Schematic of internal and external meshing pairs of planetary gear
(4)
同理,太阳轮与行星轮外啮合的曲率半径R3、R4由以下公式得到:
(5)
式中:a1和a2表示内/外啮合副中心距;rb1、rb2、rb3分别表示行星轮、齿圈、太阳轮的基圆半径。
以内啮合为例,可以确定y方向的等效曲率半径Ry为
(6)
求得曲率半径R1、R2后,可以得到啮合点大、小齿轮线速度u1、u2为
u1=ω1R1,u2=ω2R2
(7)
卷吸速度ue、滑动速度us和滑滚比ξ的定义如下:
ue=(u1+u2)/2,us=u1-u2,ξ=us/ue
(8)
式中:下标“1、2”表示行星轮和齿圈。
2 弹流润滑理论
2.1 润滑模型基本方程
文中采用弹流润滑有限长线接触模型,每一啮合瞬时等效为两反向/同向圆锥滚子的接触,热弹流润滑控制方程如下:
(9)
式中:p表示流体压力;h表示油膜厚度;ux和uy表示沿x和y方向的入口速度;ρ、η分别表示润滑剂的密度和黏度。
膜厚方程:
h(x,y)=h0+hs(x,y)+v(x,y)
(10)
式中:h0表示两接触体的刚性位移;hs表示接触表面的原始几何间隙;v表示齿面弹性变形。
hs(x,y)=ha+hb+hc
(11)
(12)
hb计算同理。
式中:ha、hb为齿轮a、b的接触表面的原始几何间隙;hc为齿顶修形引起的几何间隙;Ra、Rb为齿轮a、b的曲率半径。
由压力引起的表面弹性变形的解为
(13)
载荷平衡方程为
(14)
热弹流润滑考虑了温度对密度、黏度等参数的影响,在温升较大的极端工况条件下,建模时需在每次求解温度后更新这些参数,从而准确描述相应工况下的润滑行为。但针对温升较小的工况条件可忽略温度对这些参数的影响。PU等[10-11]研究了椭圆点接触任意卷吸方向混合润滑条件下的摩擦行为和闪温分布,并实验验证了摩擦因数计算的准确性;随后又采用同样的处理方法,进一步研究了供油不充分的乏油润滑条件下的温升。
文中以核电循环泵人字齿行星传动系统为研究对象,设计合理的齿轮啮合时温升通常较小(≤100 K),由此造成的温度和黏度变化可忽略不计。尽管忽略了温升的影响,文中模型仍可相对准确获得齿轮的润滑行为。文中密压关系采用Dowson-Higginson公式:
(15)
黏度遵循Roelands黏度-压力关系公式:
η(x,y)=η0exp[(lnη0+9.67)(1+p/(1.96×108))z-1]
(16)
指数z由以下公式得到:
(17)
式中:ρ0、η0分别为润滑剂环境密度和环境黏度;α为黏压系数。
2.2 摩擦力和闪温模型
滑动摩擦和温度上升主要产生在赫兹接触区域,润滑膜剪切应力是温度的函数,温度上升是由表面滑动摩擦引起的,混合润滑时还需考虑固-固直接接触产生的摩擦力。采用考虑温升效应的非牛顿流体模型计算润滑油膜中的剪应力:
(18)
式中,极限剪应力τL和极限剪切弹性模量G∞是压力和温度的函数,可以通过经验估计。对于典型的矿物油,可使用以下经验公式:

(19)
τL(p,T)=0.25G∞
(20)
假设润滑油的剪切应变率可以按下式近似地计算出:
(21)
于是有:
(22)
通过迭代方法求解计算网格中每个节点的上述非线性方程,可以求解油膜中剪应力τ的分布。由于润滑剂的特性对温度敏感,而温度直接受到摩擦产生热量的影响,因此表面温度和摩擦是相互影响的。文中根据半无限固体上的运动热源理论,忽略沿表面垂直于热源速度方向的热流,以及润滑剂的对流换热作用。基于上述假设,可通过求解以下方程式计算齿轮表面闪温[12]。
(23)
(24)
式中:q是润滑区域的剪切或界面摩擦产生的热量,它可以被估计为q≅τ|u2-u1|;Tb1和Tb2为两接触表面初始温度;ρ1和ρ2为密度;C1和C2为比热容;kf为热传导系数;其中剪应力τ来自公式(20)。
齿轮表面闪温计算参数如表3所示。

表3 润滑剂和齿轮的材料性能
2.3 数值方法
董庆兵团队[12-13]采用量纲一化方法建立了弹流润滑模型,研究了瞬态工况下润滑油膜的动态变化规律,为核电循环泵斜齿轮传动系统的润滑仿真提供了理论依据。文中研究对象为斜齿轮,在啮合过程中接触线长度具有时变性,齿轮和坐标系建立方法的差异性会具有不同的计算区域,因此采取具体边界数值,将齿轮每个啮合瞬时沿齿廓切线方向设为x轴,接触线沿齿宽方向设为y轴,接触线中心点为坐标原点,则计算区域如下:
{(x,y)|xs≤x≤xe,ys≤y≤ye}
(25)
为保证不同啮合瞬时的接触区域都被包含在计算范围内,外啮合计算区域边界为(xs=-0.8 mm,xe=0.5 mm;ys=-0.5b/cosβb,ye=0.5b/cosβb),内啮合计算区域边界为(xs=-2 mm,xe=1 mm;ys=-0.5b/cosβb,ye=0.5b/cosβb),b表示齿宽;βb为基圆螺旋角。将计算域沿x轴方向划分为256个均匀网格,沿y轴方向划分为512个均匀网格。运用二阶中心差分格式计算雷诺方程的左端项,运用二阶后差分格式计算公式右端楔形项,利用线松弛迭代法和逐行扫描法求解油膜压力,齿面的弹性变形采用快速傅里叶变换算法求解。压力计算的迭代因子ωp取0.01,压力收敛精度取1×10-5。
3 润滑特性计算结果及分析
3.1 接触线各节点运动参数求解结果
根据人字齿行星传动系统的几何参数和计算公式,可以求得单侧齿(即斜齿轮)啮合过程中每一瞬时啮合线中点的卷吸速度ue、滑动速度us和滑滚比ζ等时变参数的变化规律,如图4所示。内/外啮合副一个齿面从进入啮合到啮合结束的过程中,啮合线中点处滑滚比先线性增加,然后保持不变,随后继续线性增加,滑动速度与卷吸速度呈现同样的变化趋势,并且内/外啮合副接触线中心点滑滚比为0的时间段不一致。

图4 啮合线中心节点运动参数Fig.4 Motion parameters of meshing line center node: (a) for internal mesh;(b) for external mesh
图5所示为内/外啮合线各点在一个周期内的滑滚比云图,其纵坐标表示啮合线方向上,啮合线始端到末端所占用网格点数。从图中可以发现啮合线上各点的滑滚比都是在不断变化的,以滑滚比为0的等高线作为分界点,分别选取内/外啮合A、B、C、D 4处不同时刻的计算结果进行对比分析。其中B位置表示内/外啮合节点附近,此时啮合线中点处滑滚比为0。

图5 啮合副接触域滑滚比分布云图Fig.5 Distribution nephogram of slip-roll ratio in contact region of meshing pair:(a) for internal mesh;(b) for external mesh
3.2 稳态弹流润滑数值求解结果
图6所示为内啮合B、D、C 3个位置的油膜压力和油膜厚度在啮合线中点x、y方向上的变化曲线。从图6(a)中可以看出,沿x方向上,啮合前期B位置处,行星轮与齿圈接触区域前期油膜压力较大,油膜压力整体呈现先增加后减小的趋势。由于二次压力峰的存在,在出口区域的油膜形状收缩,油膜厚度会局部减小,如图6(b)所示。沿y方向上,内啮合啮合线长度先增加后减小,油膜压力与油膜厚度变化呈相反趋势的变化规律,且啮合线两端存在应力集中,如图6(c)(d)所示。这是因为内啮合的等效曲率半径逐渐增加,导致沿着啮合线方向的油膜压力和油膜厚度会呈现向一端的倾斜趋势。
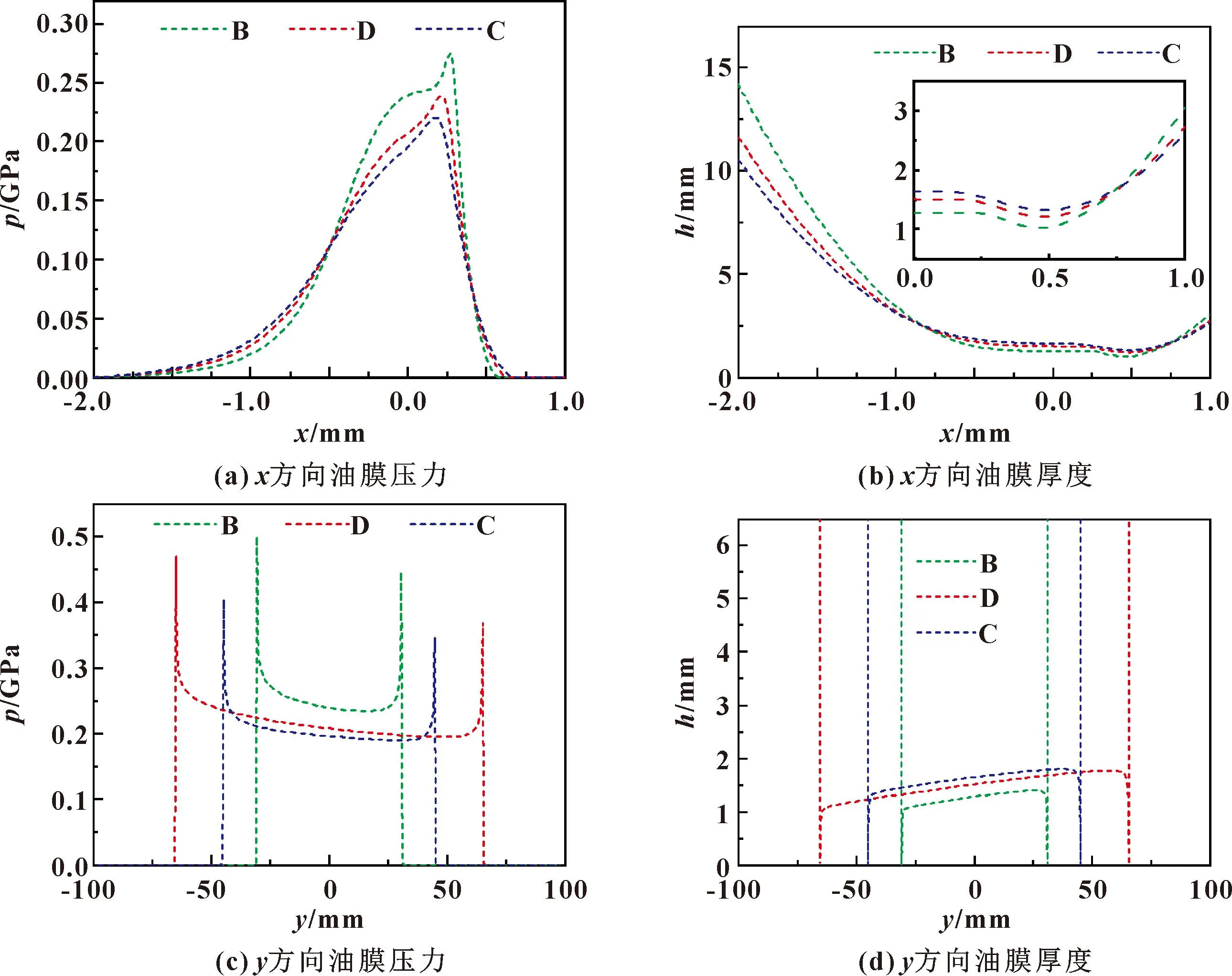
图6 内啮合弹流润滑结果Fig.6 EHL results of internal engagement:(a)oil film pressure in x direction;(b)oil film thickness in x direction; (c)oil film pressure in y direction;(d)oil film thickness in y direction
图7所示为外啮合A、B、C 3个位置的油膜压力和油膜厚度在啮合线中点x、y方向上的变化曲线。从图7(a)中可以看出,沿x方向上,外啮合前期啮合线中点处油膜压力较小,随着齿轮转动载荷增大导致中心压力增加,二次压力峰向出口方向偏移。油膜厚度在接触区域中心处无明显变化,但在出口区域二次压力峰仍会导致油膜厚度局部减小,如图7(b)所示,这是由于等效曲率半径、载荷、啮合线长度变化的综合影响所导致。沿y方向上,由于外啮合的等效曲率半径先增加后减小,沿y方向的油膜压力和油膜厚度则会呈现对称分布,啮合线两端仍存在应力集中,如图7(c)(d)所示。
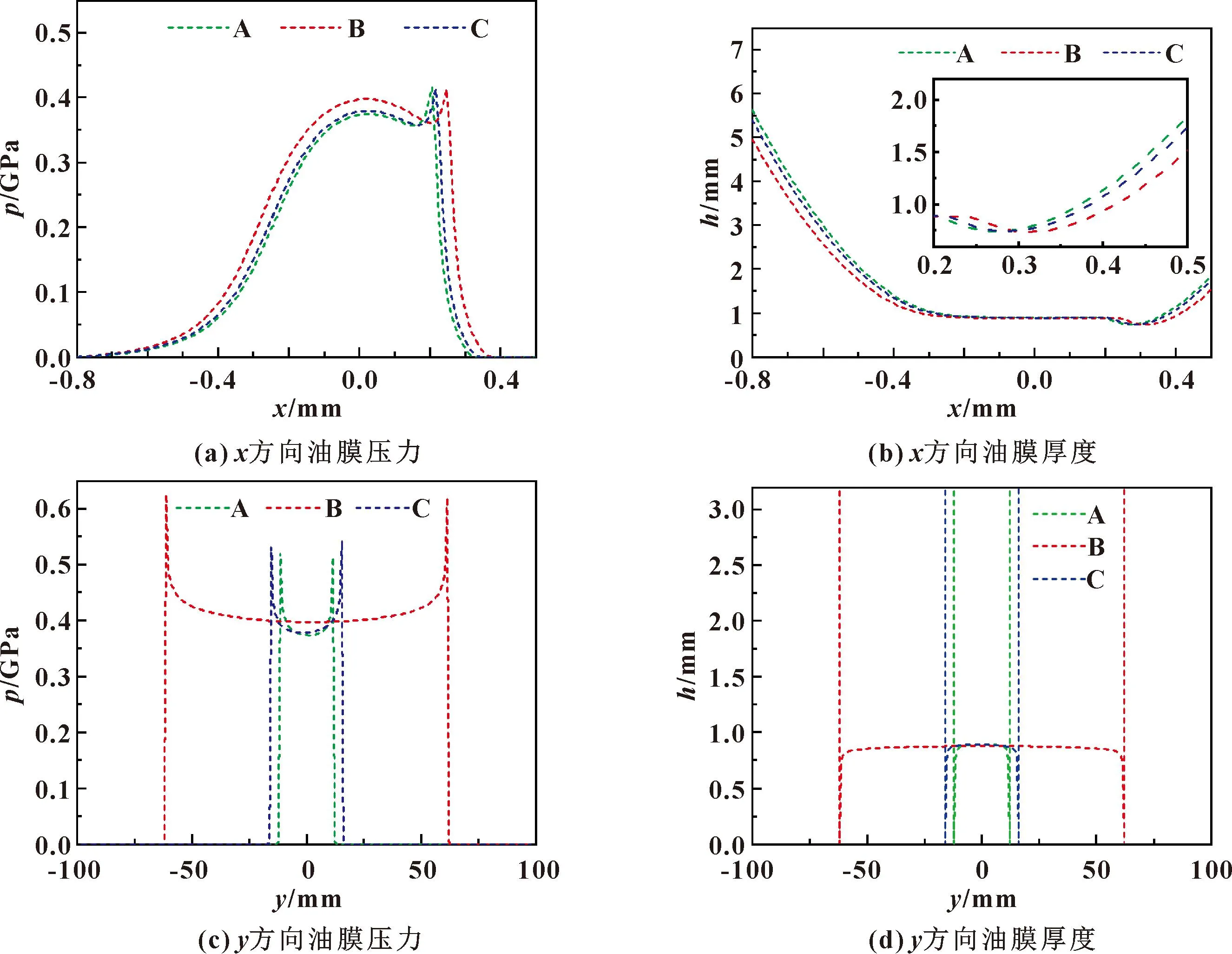
图7 外啮合弹流润滑结果Fig.7 EHL results of external engagement:(a)oil film pressure in x direction;(b)oil film thickness in x direction; (c)oil film pressure in y direction;(d)oil film thickness in y direction
3.3 齿轮表面形貌对弹流润滑性能的影响
在齿轮的实际加工过程中,齿轮表面的粗糙度数值与弹流润滑分析中的膜厚在同一数量级上,因此齿面形貌不能被忽略。文中建立的弹流润滑计算模型同样适用于粗糙表面,在公式(11)中加入实验测量得到的几何间隙,从而得到考虑齿轮表面形貌后的几何间隙,再对原始齿轮表面的粗糙度经过磨合后所形成的形貌数据进行分析处理。原始粗糙度数据采用重庆大学机械传动国家重点实验室的高集成多功能摩擦磨损试验机(MFT-5000),使用白光干涉仪实测6级加工精度齿表面得到。
文中考虑齿轮啮合过程中的磨合效应,采用移动平均滤波方法使表面变得平滑[14],采用2D过滤方法,在x、y方向上对粗糙度数据采取固定点数进行平均滤波;测量表面粗糙度时,绘制成Abbot曲线[15],用于表示磨合前后的粗糙表面变化情况[16]。滤波后的表面粗糙形貌最大值降低了30%左右,采用移动平均滤波方法过滤后的表面形貌可以代表齿轮表面磨合后的形貌进行弹流润滑计算。
以啮合线中心为坐标原点,中心油膜厚度为计算域的坐标原点,计算得到中心油膜厚度、摩擦因数、太阳轮和行星轮啮合线的中心温升以及齿面最大温升在一个周期内的变化曲线,如图8所示。对于考虑表面形貌的弹流润滑分析,中心膜厚在相应位置产生波动的同时,比光滑表面有所减小,如图8(a)所示,从而使得润滑效果变差。摩擦因数是整个计算区域所有节点剪切应力的积分和与载荷的比值,在啮合线中点滑滚比为0的位置,摩擦因数趋近于0;而在啮合中期波峰与其对应的波谷积分求和的值与光滑表面积分求和数值相差很小,因此摩擦因数波动量较小,如图8(b)所示。
图8(c)(d)所示为太阳轮和行星轮的中心温升以及齿面最大温升。在考虑粗糙度时,油膜厚度减小,剪切应力会增加,但中间位置的摩擦因数变化较小,因此中心温升变化与摩擦因数分布特点相似,各个瞬时的中心温升在剪切应力为0的位置依然为0,在其他啮合位置略微升高。而摩擦因数的整体增加,导致剪切应力增大产生更多热量,油膜温度快速升高,齿面最大温升会明显增大。因此,在弹流润滑分析中考虑齿面形貌是十分必要的。
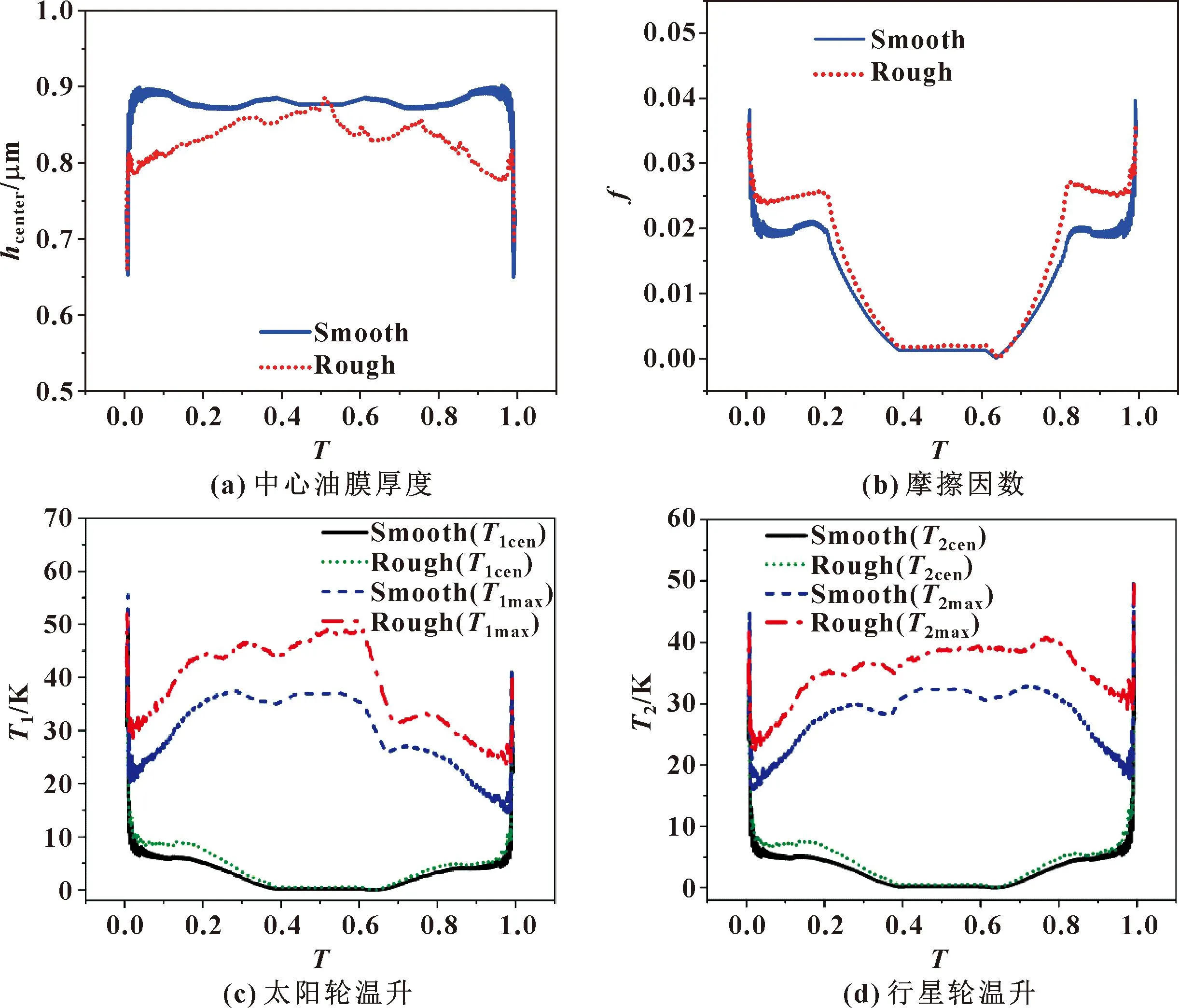
图8 考虑表面形貌影响的弹流润滑数值解Fig.8 Numerical solution of EHL considering the influence of surface topography:(a) central oil film thickness;(b) friction coefficient;(c) temperature rise of sun gear surface;(d)temperature rise of planetary gear surface
3.4 齿廓修形对弹流润滑性能的影响
由于未修形齿轮的啮合线两端存在应力集中,齿廓修形可有效改善其啮合状态,因此有必要分析齿廓修形对其润滑性能的影响。在一个啮合周期的不同位置,参与啮合的修形端是不断变化的,因此齿顶修形对弹流润滑求解的影响也是不同的。按照表2所示参数对太阳轮和行星轮进行齿顶线性修形,计算内/外啮合在B位置修形前后油膜压力在y方向的结果,如图9所示。若啮合过程中修形端未参与啮合,则啮合线长度减小,载荷会有所增加,导致油膜压力增加,如内啮合B位置,见图9(a);若修形端两侧都参与啮合,油膜压力两侧都会降低,如外啮合B位置,见图9(b)。
图10所示为外啮合副在B位置啮合线计算域的剪切应力以及齿面温升。图10(a)所示为y=40 mm处的齿面温升在x方向的分布曲线,T1表示太阳轮表面温升。同方向的剪切应力和齿面温升分布特点相似,修形后的温升和剪切力在x方向都会稍微增加,齿面温升出口大于0。这是因为处于边界区域时太阳轮和行星轮接近环境温度,中间过程通过剪切运动产生热量,导致齿面温度升高;而由于二次压力峰的存在,出口油膜剪切力比入口大,产生更多的摩擦热,温度降低缓慢,所以出口温度高于入口温度,但x方向的剪切力入口和出口边界都为0。图10(b)所示为y方向剪切应力变化曲线,根据修形结果图9(b)所示,啮合线两端应力集中减小,则剪切应力也随之减小,齿面温升也会有所下降。因此,在弹流润滑分析中考虑齿轮修形是十分必要的。

图9 修形对啮合位置B油膜压力的影响Fig.9 Influence of profile modification on oil film pressure at position B:(a)for internal mesh;(b)for external mesh

图10 齿顶修形对剪切应力和齿面温升的影响Fig.10 Influence of tooth tip modification on shear stress:(a) xdirection tooth surface temperature rise;(b) y direction shear stress
4 结论
针对行星轮内/外啮合齿轮副,考虑非匀布的载荷分配特性解析得到内/外斜齿轮啮合过程中接触区域的运动参数变化规律,将行星轮齿轮副啮合状态几何等效为圆锥滚子的接触问题,建立典型工况下斜齿轮线接触热弹流润滑计算模型,分析了计算域中各节点的油膜厚度、油膜压力、剪切应力和温升分布情况,研究了轮齿表面形貌和齿廓修形对弹流润滑性能的影响。主要结论如下:
(1) 内/外啮合副在啮合过程中的等效曲率半径、卷吸速度和滑滚比等参数的变化有所不同。在啮合前期和后期,内/外啮合的啮合线长度较短,油膜压力较小,接触线上不存在滑滚比为0的点。在啮合中期,油膜压力较大,啮合线两端存在应力集中,膜厚较小,内/外啮合接触线上存在滑滚比为0的点,剪切应力在啮合线上呈现正负交替变化。
(2) 考虑齿面粗糙形貌时,中心油膜厚度比光滑解减小,粗糙度的存在弱化了油膜承载能力。在轮齿啮合前期和后期,摩擦因数增大比较明显,中心摩擦因数波动较小;考虑粗糙度的齿表面最大温升有明显的增大趋势,这与接触压力的增加导致剪切应力增大有关。因此,在热弹流润滑模型的精密计算中考虑粗糙度的影响是十分必要的。
(3) 对太阳轮和行星轮进行齿廓修形,研究发现油膜压力和油膜厚度减小与参与的啮合修形端数量有关;修形后剪切应力与齿面温升变化规律相似,但两者受到摩擦因数、修形量和载荷分配等多种因素的综合影响;合理的修形可以有效降低啮合端的应力集中,减小油膜压力、油膜厚度、剪切应力和齿面温升,改善啮合线终端的润滑状态。
