海沟影响下深水海洋管线成环行为研究
2024-03-12贾纪川顾继俊陈磊磊
贾纪川,顾继俊,黄 俊,高 磊,,陈磊磊
(1.中国石油大学(北京) 机械与储运工程学院,北京 102249;2.中海油研究总院有限责任公司,北京 100028)
立管、电缆和系泊缆是海洋石油管线系统的重要组成部分。研究表明,在安装和在位运行过程中,由于制造工艺的偏差、上部浮体的运动以及海洋环境的影响,海洋管线可能存在不均匀的扭矩分布,从而造成扭转失稳现象的发生,图1(a)所示为典型的海洋柔性立管扭转现象[1]。在海洋管线的扭转行为中,一种较为极端的情况是“成环”。在张力和扭矩的共同作用下,海洋管线系统可能出现局部成环现象,当管线所受的张力增大时,环的半径会相应减小,从而进一步形成扭结,如图1(b)所示,为实际工程中柔性立管的打结现象[2]。

图1 立管典型扭转行为Fig.1 The typical torsional behavior characteristics of a riser
试验测试和数值计算是分析海洋管线成环行为的主要方式。试验测试方面:Vachon[3]使用竖直放置的钢缆样品完成了扭结形成试验,以分析海上系泊缆的成环特性;Liu 和Center[4]在试验中将电缆样品垂直悬挂在钢架下,同时施加扭矩和张力,使其成环,并分析了管线成环状态与管线自身力学特性之间的关系;Yabuta 等[5]和Yabuta[6]使用小直径的光纤作为试验测试样本,以研究不同位移模式下的电缆环“打开”现象,并分析了电缆环保持稳定性的条件;Goss[7]和Goss等[8]将小段镍钛诺杆夹持在水平加载装置上,通过扭转杆端和调整杆的松弛度以模拟环的形成,并分析了不同输入扭矩、松弛度以及自身重力等因素对样品成环行为的影响。
数值计算方面:Zajac[9]和Rosenthal[10]基于弹性理论研究了电缆形成环或者扭结的临界载荷;Knapp[11-13]基于能量法建立了理论方程,以分析笔直的电缆在拉伸和扭转共同作用下的响应,对应的计算程序则可以有效处理一端自由或两端固定的电缆扭转成环问题;Goyal等[14-15]、Goyal和Perkins[16-17]基于基尔霍夫杆理论建立了动态数值模型,以捕捉管线不同状态之间的动态转换过程,并指出了该理论在海洋管线扭转行为和DNA 超螺旋状态研究中的应用前景,随后在此基础上提出了一种包含12阶杆单元模型和6阶杆单元模型的杆—悬链线混合模型,以有效分析船用海缆的动态弯曲和扭转行为,与传统的悬链线模型相比,该混合模型的计算效率提高了1.5~2.0倍;Neto等[18-20]、Neto和De arruda matrins[21]、Neto[22]提出了一个精确的非线性三维动态梁单元模型,并基于该模型对海洋立管成环过程中涉及的扭转稳定性、管线自接触、海流作用及管土摩擦等问题均做了深入研究;Zhang 等[2]使用OrcaFlex 软件研究了在扭转、拉伸等外部载荷共同作用下海洋立管的成环机理,并完成了相关的可靠性分析。
对于前述研究,从研究对象的角度看,由于试验条件的限制,试验测试通常以直杆或者直缆作为海洋管线成环研究的试验样本;而数值计算的研究对象相对广泛,包括电缆、系泊缆和海洋立管。从研究内容的角度看,无论是试验测试还是数值计算,前人的研究主要集中在成环的机理上,对于环境因素对海洋管线成环的影响研究较少。Goyal 等[14]、Neto 等[18]和Zhang 等[2]均指出海洋管线的成环区域位于其触地区附近,而该部分区域恰是海沟易形成的区域[23-25]。因此下文采用海洋工程有限元分析软件OrcaFlex,就海沟对立管成环的影响开展相关研究,主要分析海沟轮廓、海沟位置及海沟土壤属性对成环过程中立管相关力学特性的影响,并考虑了立管成环过程中临界载荷的变化。
1 力学模型
1.1 管线模型
使用有限元软件OrcaFlex框架下的管线模型[26]来建立研究所需的基本海洋立管模型。
管线模型基于集中质量法建立,由多个单元组成,单元之间通过末端的节点连接。每个单元的质量为0,并等效于由弹簧阻尼器连接的2个弹性杆,以此模拟管线模型的轴向拉伸、压缩和扭转特性。
OrcaFlex 框架下的管线模型如图2 所示。模型中每个节点的质量为与其相连的2 个单元质量总和的一半,管线模型2个末端节点除外,其质量为与之相连的单个单元质量的一半。组成管线模型的单元所受的重力、浮力、水流力以及海床作用力均集中分配到各个单元节点上。

图2 OrcaFlex管线模型Fig.2 The pipeline model in OrcaFlex
管线的平衡方程为[27]:
式中:R是关于位置变量x、y、z和时间变量t的矢量函数;m是管线模型的单元质量;Te是有效张力[28];sɛ是管线单元变形后的长度;V是分布载荷;wf是模型单元所受的浮力;weh是单元所受的水流力;wg是单元所受的重力;wsd是单元所受的海床土反力;M是截面弯矩[28]。
1.2 管土作用模型
OrcaFlex 中引入了4 种模式以表征海洋管线与海床之间在垂直方向上的相互作用过程,包括未接触模式、初次贯入模式、抬升模式和再贯入模式[29]。
图3展示了当贯入深度z值改变时,海床土阻力P(z)的变化。管线初步接触海床,采用初次贯入模式计算土阻力。
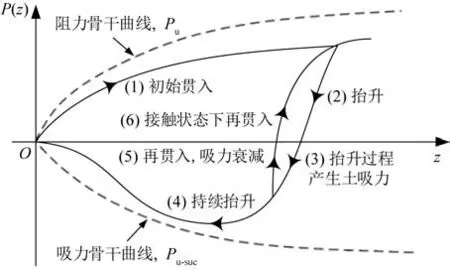
图3 管土作用曲线Fig.3 Pipe-soil interaction curve
随着贯入深度的增加,土阻力逐渐接近极限土阻力Pu。随后,管线开始抬升,此过程采用抬升模式进行计算。在抬升过程中,土阻力的值逐渐降低,而土吸力Pu-suc的值开始增加。当抬升距离达到一定程度时,土吸力接近其极限值。当土吸力达到极限值后,若抬升过程继续,则土吸力开始减小并将最终降至0;另一种情况则是抬升过程在土吸力达到极限值后终止,管线开始再次贯入海床,此时模式转变为再贯入模式。在再贯入模式中,随着贯入深度的增加,土吸力值开始减小,而土阻力值Pu(z)开始再次增加,并最终接近极限土阻力。抬升和再贯入过程的往复循环,将导致管线在海床上的贯入深度逐渐增加。
土阻力和吸力方程:
式中:Pu(z)为海床土阻力;Nc(z/D)为承载因子;D为管线直径,Su(z)为土壤剪切强度;Su0为海床表面不排水抗剪强度;r为抗剪强度梯度;Pu-suc为土吸力;fsuc为吸力因子。
采用修正的库仑摩擦模型对水平方向上的管线—土壤相互作用过程建模。海床土壤对管线施加的水平力如图4所示。如果水平力小于克服土壤摩擦的最小力,则假定土壤为线弹性,水平力和管线位移之间的关系如下:
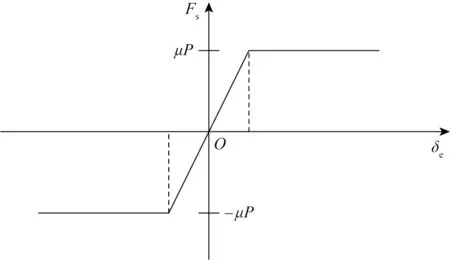
图4 管土作用库伦摩擦模型Fig.4 The Coulomb friction model for pipe-soil interactions
式中:Ks是土壤的水平刚度;δe是土壤的横向变形。
如果水平力大于克服土壤摩擦的最小力,则假定水平方向上的土壤作用力为摩擦力,该摩擦力与垂直方向上的海床土反力成正比,关系表达式为:
式中:μ是摩擦因数;P是垂直方向上的海床土反力。
1.3 海沟模型
海沟是由立管和海床土壤之间的相互作用形成的,海沟的存在会显著影响触地区立管段的性能[23-25]。研究采用经验公式构建海沟轮廓,并分析其对立管成环的影响。Wang和Low[24]提出了一种参数公式来描述海沟的轮廓,娄敏等[25]则对该参数公式进行了改进,使其能够更准确地描绘海沟剖面。研究采用了娄敏等[25]提出的经验公式,以生成不同长度和深度的海沟模型。
构建海沟模型如图5所示。参考点(RTDP)指平坦海床上立管的触地点。随着海沟的延伸和扩展,立管在海沟内的触地点(TDP)会沿着海沟的左侧(以海沟最大深度点为分界点,靠近海沟起始点的一侧)移动。ΔTP表示RTDP 与海沟起始点(TBP)之间的距离;LT表示点TBP 与海沟终止点(TEP)之间的水平距离,即海沟的长度;dmax表示海沟的最大深度;Lmax表示TBP和海沟最深点(TMP)之间的水平距离。
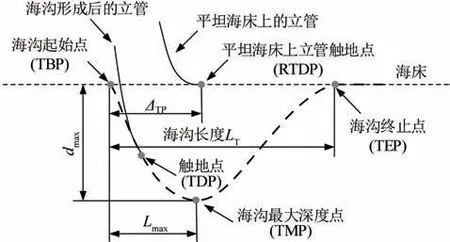
图5 典型海沟轮廓示意Fig.5 A sketch of a typical trench profile
构建海沟模型的3个主要参数分别是LT、dmax和ΔTP,其中LT和dmax确定海沟的基本尺寸,ΔTP确定海沟的位置。LT和dmax的值基于娄敏等[25]提出的经验公式获得:
其中,
式中:Rd、Rm、RHV、RL和RTP均为无量纲参数;D是立管外径;m是立管单位长度的质量;ρ是海水密度;H是立管顶部悬挂点(HOP)和RTDP 之间的水平距离;V是HOP 和RTDP 之间的垂直距离。D、m、ρ和V的值见表1 和表2。H的值在OrcaFlex 中通过静力计算获得,为303 m。将式(9)代入式(7)和(8),可得到RL和RTP的值,再将RL和RTP的值代入式(10),可得到LT和ΔTP的值,至此确定了海沟的位置和长度。

表1 立管参数Tab.1 Riser parameters
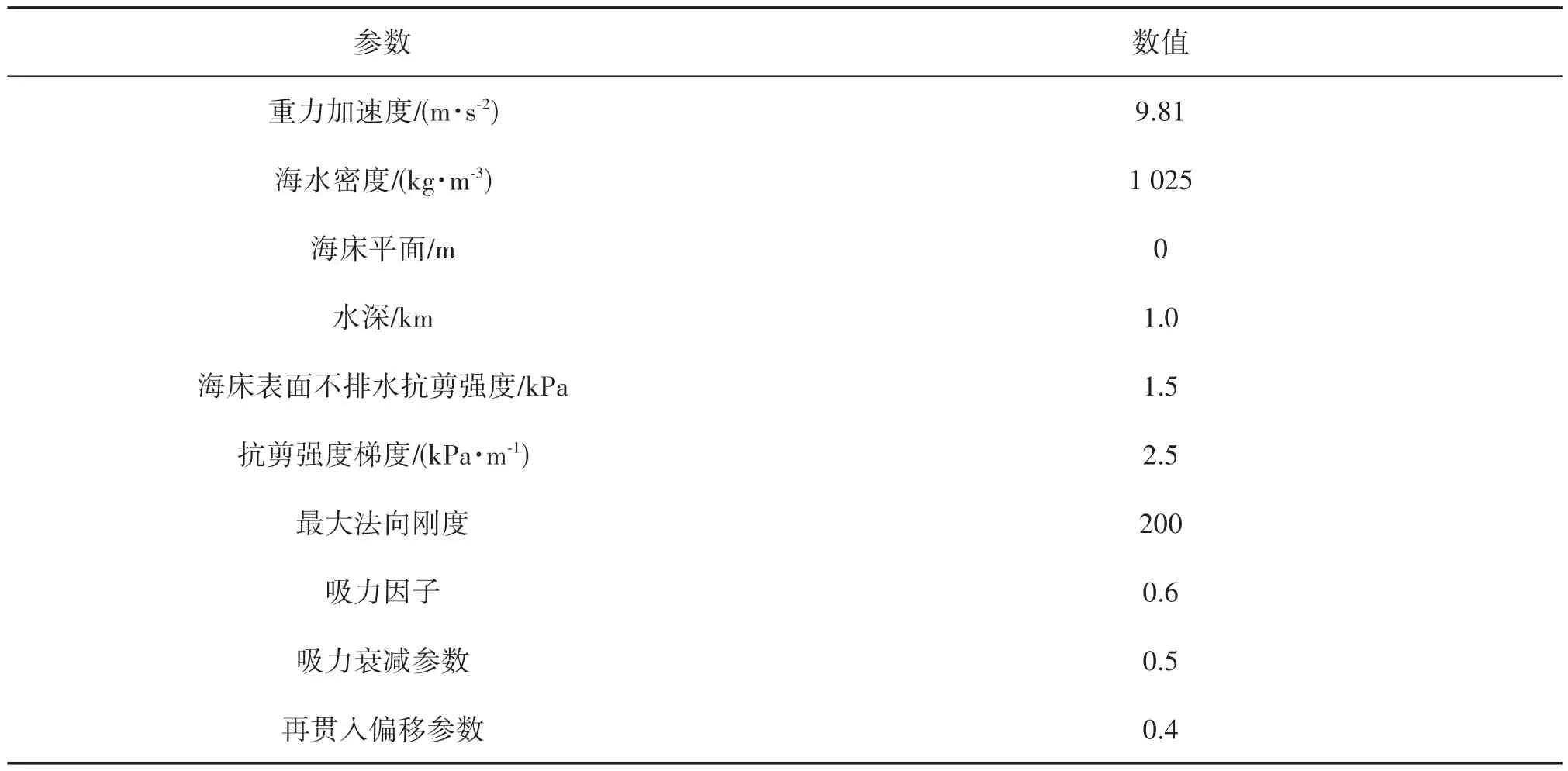
表2 环境参数Tab.2 Environmental parameters
海沟基本形状的构建是参考Aubeny和Biscontin[30]提出的三次多项式:
2 成环参数分析
2.1 立管成环属性
参考Neto等[19]和Zhang等[2]的参数设置,选择深水海洋管线中较为常见的钢悬链线立管作为研究对象,立管的几何与材料参数如表1所示。
在环境参数中,为贴近实际工况,选择非线性海床模型作为研究模型,涉及海床表面不排水抗剪强度、抗剪强度梯度和吸力因子等非线性土壤参数的设定,所有环境参数如表2所示[19,24]。
为了便于分析海沟上的立管成环行为,参考Neto 等[18]研究中提出的施加载荷方式,在立管的顶点缓慢加载线性扭矩,如图6所示。
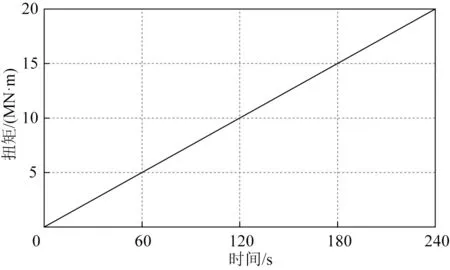
图6 在立管顶点线性施加扭矩Fig.6 The linearly applied torque at HOP
研究以Neto等[20]提出的“自接触状态”作为立管成环的极限状态,此时立管环为完整的闭环。在平坦海床上,成环的立管与悬链线状态下的立管对比如图7所示。重点对比了2种状态下立管的整体形态、轴向应力分布和曲率分布,轴向应力基于规范《DNV-RP-F204》[31]计算得到,计算公式为:
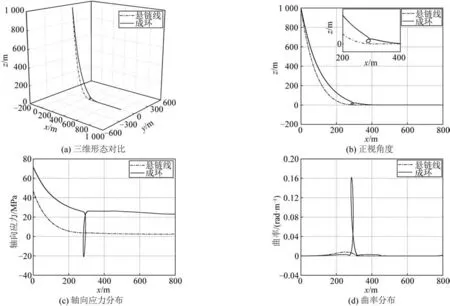
图7 立管悬链线状态和成环状态对比Fig.7 Comparison between catenary state and loop formation state of riser
式中:σa表示轴向应力;Te表示有效张力;D表示立管外径;t表示立管壁厚。
在转驱时机优化中,主要考虑转驱时的油藏压力和井间的热连通性。在蒸汽吞吐中,第2周期到第4周期加热半径和加热区域不断扩大,到第4周期,井间已经建立起热连通。第5周期,其加热区域扩大较为缓慢,主要起到重复加热地层的作用。综合考虑蒸汽驱阶段油汽比、采收率和净采油量等因素,推荐在蒸汽吞吐4周期以后转驱,采收率可达27.1%。
在图7(a)中,当立管形成环时,成环处的立管段在x、y、z三个坐标轴方向上均存在一定偏移距离。从正视角度,基于图7(b)及其局部放大图可以发现,成环的位置位于悬链线立管的触地区附近。随着立管环的形成,沿立管分布的轴向应力整体变大,最大轴向应力位于立管悬挂点处,如图7(c)所示。通过对比图7(b)和图7(c)可以发现,在立管成环位置处轴向应力出现负值,说明存在局部压缩,最大压缩力可通过该点有效张力的绝对值体现。在图7(d)中,当立管环形成时,沿立管的曲率分布与悬链线状态下大致相似,不同之处在于成环位置处会出现曲率的极值,说明此处弯曲程度最大,在参数分析中可通过最大弯矩体现。
2.2 海沟轮廓的影响
基于1.3节构建海沟轮廓的经验公式,在OrcaFlex中建立深度为0.5D到5.5D的海沟模型,海沟系统的原点与图7 系统的原点保持一致,且后文海沟系统的建立均遵循这一规则。不同深度海沟如图8 所示。分析随着管土作用的持续进行,海沟轮廓的扩展对立管成环行为的影响。
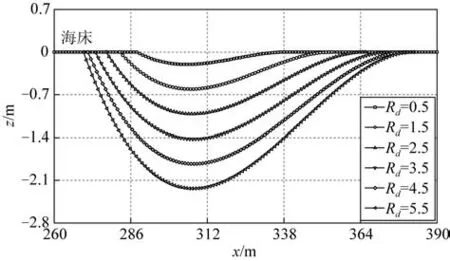
图8 不同长度和深度的海沟Fig.8 Trenches at varied lengths and depths
图9展示了不同海沟轮廓对立管成环行为的影响。如图9(a)所示,随着海沟深度和长度的增加,立管环的位置呈现下沉趋势。从俯视角度,环的开度也随着海沟的扩展而增加,如图9(b)所示。分析原因为:随着海沟的扩展,其深度和长度增加,立管位于海沟上方的悬空段逐渐变长,失去了海床土反力的支持,在自身重力的作用下,立管环将呈现下沉趋势;随着环的下沉,立管张紧,立管环将逐渐脱离自接触状态,导致环路的打开。

图9 不同海沟轮廓对立管成环的影响Fig.9 The influence of varied trench profiles on the riser loop formation
随着立管环脱离自接触状态,由立管成环导致的局部压缩逐渐减小,压缩力的最大值呈现下降趋势,如图9(c)所示;与之相对应,立管的局部弯曲程度也会有所降低,最大弯矩值同样呈现下降趋势,如图9(d)所示。
2.3 海沟与立管环相对位置的影响
以深度是3.0D的海沟为基础,调整海沟起始点坐标为275、271、267、263、259和255 m,分别对应图10中的位置1 到位置6,研究立管在海沟不同位置处成环时力学属性的变化。其中在位置6 时,立管环处于海沟最深点正上方。
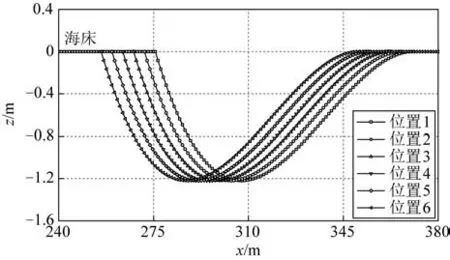
图10 不同海沟位置Fig.10 Trenches at various locations
图11展示了当立管环处于不同的海沟位置时,立管力学属性的变化。从图11(a)和11(b)可以看出:随着立管环从海沟的边缘地带向最深点平移,其开度逐渐减小,当到达海沟最深点正上方时,立管已形成完整闭环。原因在于:随着立管环的位置向海沟最深点正上方靠近,环两侧悬空的立管段的长度差值逐渐减小,与之对应的,是两侧施加在立管环上的拉力差值的减小,从而使其更易达到平衡状态;相对而言,在海沟边缘处,立管环承受单侧悬空管段的影响,更易呈现“打开”状态。
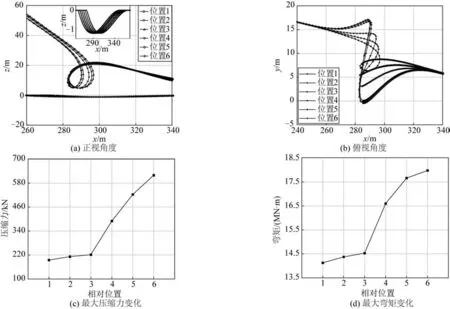
图11 不同位置海沟对立管成环的影响Fig.11 Influence of various trenches at different locations on the riser loop formation
随着立管环向海沟最深点的正上方靠近,立管逐渐达到自接触状态,与之对应的是立管成环处,最大压缩力和最大弯矩的逐步增大,如图11(c)和11(d)所示。
2.4 海沟土壤属性的影响
如图7(a)所示,立管在成环过程中既有平移运动也有抬升运动,平移运动涉及立管与海床表层土壤之间的摩擦,抬升过程中立管则可能受到土吸力的影响。因此本节基于上述2个方面,选择非线性土壤参数中的海床表面不排水抗剪强度Su0和吸力因子fsuc作为研究参数,分析其对海沟上立管成环行为的影响。以深度是3.0D的海沟模型为基础,在海沟处,立管环在2 个典型土壤参数影响下的力学性能变化如图12 和图13所示。
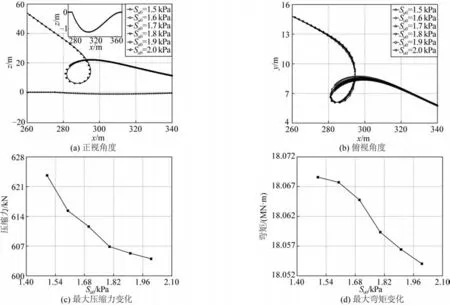
图12 不同Su0对立管成环的影响Fig.12 Influence of various Su0 on the riser loop formation
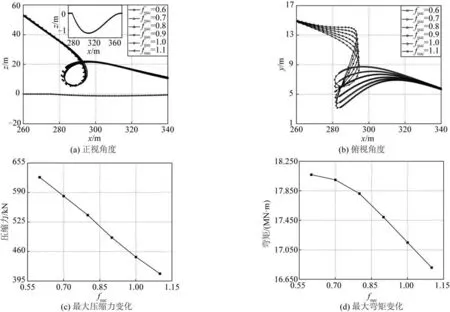
图13 不同fsuc对立管成环的影响Fig.13 Influence of different fsuc on the riser loop formation
如图12 所示,随着Su0的增大,立管环呈不明显的打开趋势,与之对应的是压缩力和弯矩的最大值均呈现下降趋势。
Su0是表征海床刚度的关键参数[32],Wang等[33]指出较高的抗剪强度对应较硬的海床。Chen等[34]则发现,较高的Su0值对应较大的海床土阻力。因此,结合第1.2 节中的式(6)可知,Su0的增大将导致垂直方向上海床施加给立管的土反力增大,即式(6)中的P值增大,从而导致立管受到的海床土壤摩擦力Fs增大,使得立管环在向自接触状态转化的过程中,在水平运动方向上受到更大的阻力。因此,随着Su0的增大,立管环的开度会增大,与之对应的是最大压缩力和最大弯矩的减小,如图12(c)和12(d)所示。
图13 展示了不同吸力因子fsuc对立管成环的影响。与Su0类似,随着fsuc的增大,立管环逐渐打开,压缩力和弯矩的最大值均呈现下降趋势。通过对比立管环力学属性的变化范围可以发现,在增长速率相同的情况下,fsuc对立管成环的影响程度大于Su0。
在立管环形成的过程中,立管整体呈现抬升趋势。Wang 等[33]指出,当立管开始向上运动时,土壤对立管的作用力将转化为土吸力。Shiri[35]则通过研究证明土吸力的大小主要由吸力因子fsuc决定,较大的fsuc对应较强的土吸力[36]。因此可以推断,在立管成环过程中,随着fsuc的增大,立管所承受的土吸力增大,立管环向自接触状态转化的过程受到阻碍,从而导致立管环开度的增加及相应力学属性的变化。
3 临界载荷
Neto等[19]通过监测立管端部的旋转角度并绘制扭矩—转角曲线图来初步判断立管成环过程的稳定性,这里参考该方法,在立管顶点线性施加扭矩的情况下,实时监测立管顶点的旋转角度。由于fsuc对立管成环行为的影响相对较大,本节选取不同的fsuc值,分析不同工况下立管成环的临界载荷。
图14 所示为不同fsuc对应的扭矩—顶部转角曲线图。随着旋转角度的增大,在立管顶部施加的扭矩呈现迅速增加—缓慢增长—逐渐稳定的变化趋势。通过对比发现,当旋转角度达到368°时,施加的扭矩基本达到临界状态并保持稳定,此时立管在触地区基本形成完整的闭环。图14 中的局部放大图以及表3 显示,随着fsuc的增大,立管成环的临界扭矩也会增大。此外,图14 还显示,尽管不同fsuc作用下立管成环的临界扭矩有所不同,但扭矩从迅速增加状态到缓慢增长状态的转折点却基本一致,该点对应的顶部旋转角度为45°,扭矩为9.4 MN·m。

表3 立管成环的临界扭矩对比Tab.3 Comparison of critical torque of riser loop formation
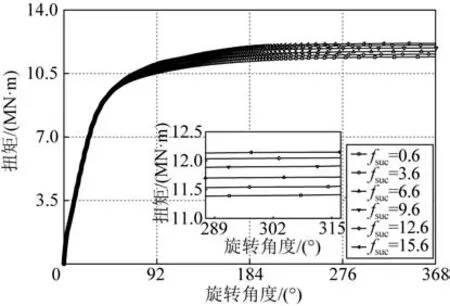
图14 扭矩随立管顶部旋转角度的变化Fig.14 Variation of torque with increasing rotation angle at HOP
除临界扭矩之外,由于立管顶部的旋转角度会直接影响立管成环的进程,因此有必要分析不同fsuc对立管顶部旋转角度的影响。以fsuc=0.6时的临界扭矩11.425 0 MN·m为基准,对比施加相同扭矩时,不同fsuc作用下立管成环的旋转角度。图15和表4显示:对立管施加相同扭矩时,随着fsuc的增大,立管顶部旋转角度呈现下降趋势。说明fsuc的增长不仅会提高立管成环的临界扭矩值,在施加相同扭矩的情况下,fsuc数值的增大还会减小立管顶部的旋转角度,从而降低成环速率。

表4 施加相同扭矩时旋转角度对比Tab.4 Comparison of rotation angles when applying the same torque
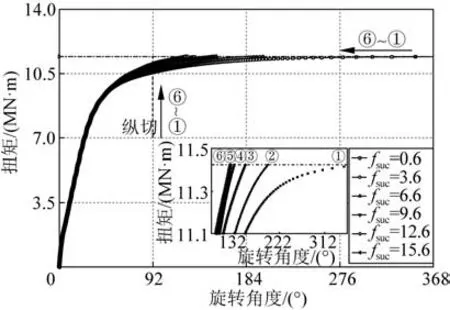
图15 相同扭矩下的旋转角度Fig.15 Rotation angles at the same torque
4 结 语
基于管线集中质量模型、非线性土壤模型和海沟经验模型,在OrcaFlex框架下建立了海沟作用下的深水悬链线立管成环模型,研究了立管成环的基本特性和海沟对立管成环行为的影响,并分析了立管成环的临界载荷。具体结论如下:
1) 在顶部扭矩和非线性海床的共同作用下,立管可能在其触地区成环。当立管环达到自接触状态时,在立管的成环处会出现压缩力和弯矩的极值。
2) 海沟的延伸扩展、海沟的位置以及海沟的土壤属性均对立管的成环行为存在规律性的影响。其中,海沟深度和长度的增加,立管环从海沟最深点向海沟边缘的平移,以及海沟土壤参数Su0和fsuc的增大,均可提升立管环的开度,降低立管成环过程中的最大压缩力和最大弯矩,从而减少成环行为带来的损伤。
3) 扭矩—顶部转角关系的研究表明,随着立管顶部旋转角度的增大,所施加的扭矩呈现迅速增加—缓慢增长—逐渐稳定的变化趋势,fsuc数值的增大将导致立管成环临界扭矩的增加和成环速率的降低,但外部扭矩从迅速增加状态到缓慢增长状态的转折点是基本一致的。
研究表明:合理的海沟轮廓、海沟位置和海沟土壤属性可有效降低立管成环带来的损伤,并可通过预测临界载荷避免完整立管环的形成。研究成果可以为非线性海床上海洋管线扭转成环问题的相关研究提供参考。
