深海采矿转场工况平台—水下系统耦合动力响应特性研究

沈玉琦，李 焱，刘汇海，唐友刚

（1.中国船舶集团有限公司第七〇八研究所，上海 200011；2.天津大学 建筑工程学院，天津 300350；3.天津大学 水利工程智能建设与运维全国重点实验室，天津 300350）

海洋中尤其深海储藏矿石极为丰富［1-3］，中国于2001年获得世界大洋协会授权开采太平洋CC 区的深海矿藏，水深范围5.0 km以上［3-4］，这里研究的深海矿产开采装备，适合于6.0 km深水采矿。

采矿系统包括水面多功能采矿平台、矿浆管道水力提升系统、海底自行式矿石集矿车。矿浆管道又称为输浆管，一般由钢管和浮力材料构成，浮力材料外包在钢管外层。海底自行式矿石采集系统主要设备是矿石采集车［4-5］。

深海采矿作业主要是转场和采矿工况，其中转场工况，由于采矿平台航行使输浆管遭受更大海流作用，因此更为危险。谢梦琪等［6］研究采矿系统的不同撤离方案对采矿系统安全的影响，尤其指出悬挂输浆管整体撤离的危险因素。肖林京等［7］等进行了采矿船与输浆管耦合系统的试验研究，但试验模拟的中继站质量（50 t）偏小。陈智昊等［8］和宋环峰等［9］采用集中质量法，以采矿船运动作为边界条件，计算输浆管动拉力和中继站运动等。

叶帆和晏莎［10］使用AQWA 程序计算采矿船的幅频响应及输浆管连接点的弯矩。Hong［11］建立了采矿船—输浆管—中继站的耦合模型，输浆管底端自由，基于集中质量法离散输浆管，分析输浆管纵向振动。Kim等［12］建立了采矿船—扬矿硬管—中继站的耦合模型，基于模态叠加法模拟输浆管的运动。Song等［13］建模与叶帆和晏莎［10］类似，研究采矿船与输浆管连接位置的相互作用。

目前国内外的研究工作，采用采矿船—输浆管—采矿时域全耦合的计算较少，一般是分别建立采矿船及输浆管模型，以采矿船运动作为边界条件，计算输浆管的动力响应。该方法计入了采矿船对输浆管的影响，而没有计入水下系统对采矿船运动影响，目前计算过程忽略了采矿船动力定位的影响，此外对于输浆管的浮力材料也未考虑。

研究工作的创新在于：建立采矿平台—输浆管—浮力材料—中继站一体化耦合动力计算模型，考虑风浪流载荷及动力定位作用，系统研究采矿系统的动力响应，评估推进器的可靠性，其中输浆管采用梁单元模拟而不是集中质量法模拟，可得到输浆管的轴力、弯矩在内的所有内力。

1 数值方法及输浆管阻力系数

水动力载荷计算包括一阶波浪力和二阶波浪力，平台的运动方程如下［14］：

式中：M表示平台质量的惯性矩阵；Aω表示频域附加质量矩阵；C表示随频率变化的阻尼矩阵；D1、D2分别表示一阶、二阶阻尼矩阵；K表示静水刚度矩阵；q(t)表示平台所受风浪流力，此处考虑DP 推进力，q(t)中包括动力系统推进器的推力；x″、x'、x分别表示平台的加速度、速度和位移。

波频内平台的运动方程为［14］：

式中：x″HF、x'HF、xHF分别表示平台波频运动的加速度、速度和位移；qw1(ω)表示一阶波浪力。采用卡尔曼滤波器对波浪中的波频成分进行过滤。

经卡尔曼滤波器滤去波频成分，时域内船舶运动方程为［14］：

式中：A0表示频率为0 时平台的附加质量矩阵；x″LF、x'LF、xLF分别表示平台的低频加速度、速度和位移；qw2(ω)表示二阶波浪力；qext(t)表示风载荷、流载荷、推进器推力和其他外部力的总和。基于式（3），DP 系统对于平台低频运动进行运动定位控制。

波浪谱采用三参数JONSWAP谱来计算波浪载荷，JONSWAP谱表达式：

式中：Hs为有效波高；Tp为谱峰周期；α为无因次风区函数；ωm为谱峰周期对应的频率；γ为谱峰升高参数，视海浪情况而定，平均值为3.3；σ为峰形系数。风力和海流力基于文献［15］计算。

输浆管与平台底部连接，其下端连接中继站。输浆管由Morison公式计算水动力［14］：

式中：F是单位长度输浆管所受的总水动力矢量；FD是输浆管与流体因相对速度所产生的拖曳力矢量；FI是输浆管与流体因相对加速度所产生的惯性力矢量。

考虑输浆管的构型会发生弯曲和倾斜，拖曳力矢量不仅包括法向力还包括切向摩擦力，拖曳力矢量FD为：

式中：CD为法向阻力系数；CT为切向阻力系数；ρw为海水密度；D为输浆管直径；Vn为输浆管和海水质点法向相对速度矢量；Vt为输浆管和海水质点切向相对速度矢量。

惯性力矢量FI为：

式中：CM为惯性力系数，取2；V̇n为输浆管和海水质点法向相对加速度矢量。

根据规范《DNVGL-RP-C205》［16］，输浆管阻力系数与表面粗糙度和雷诺数有关，分别计算浮力管段和钢管段的阻力系数，计算结果如表1所示。

表1 浮力管和钢管在不同流速下的CDTab.1 Normal resistance coefficient of buoyancy tubes and steel tubes at various flow rates

2 采矿平台建模及幅频响应计算

2.1 计算模型

采矿平台和输浆管的技术参数如表2和表3所示。

表2 采矿平台主要技术参数Tab.2 Main technical parameters of mining platforms

表3 输浆管技术参数Tab.3 Technical parameters of slurry pipes

输浆管浮力材料布置为：浮力管长2.0 km，自水面开始向下布置，如图1所示。

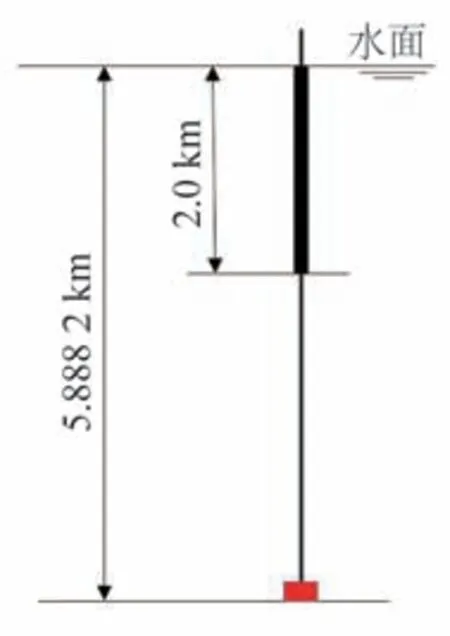
图1 浮力材料布置方案Fig.1 The layout plan of buoyancy materials

输浆管上端水面以上部分，高11.8 m，不设浮力管。输浆管与平台底部铰接，中继站下端与软管连接，如图2所示。软管对于中继站运动有一定位移限制作用，但不限制中继站的转动，所以可取为3个线弹簧。由于输浆管顶端与平台铰接，为了计算输浆管的轴力弯矩等，需要排除软管的刚体位移，所以在中继站的下端施加3个刚度系数很小的弹簧，以便排除输浆管及中继站的刚体位移。

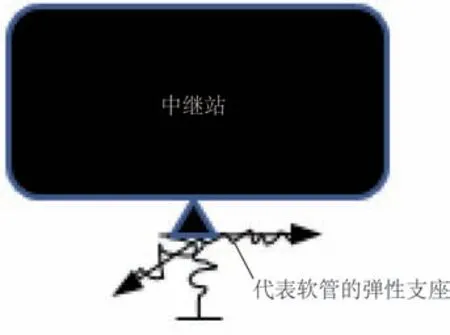
图2 中继站下端的边界条件Fig.2 Boundary conditions at the lower end of the relay station

经过试算，取3个线弹簧的刚度系数为钢管刚度系数的1/1 000时，便可以有效排除中继站的刚体位移，保证计算的收敛性。3个弹簧刚度系数取钢管刚度系数的1/1 000，即：

式中：E为钢管弹性模量；A为钢管的截面积。

输浆管水面以下长度为5.888 2 km，水面以上连接到平台底部的输浆管长为11.8 m，因此，图3（b）中输浆管的长度为5.888 2+0.011 8=5.9 km。采矿平台水下部分采用网格离散计算水动力，输浆管采用梁单元离散，单元长度10 m。平台和输浆管几何模型如图3所示。

图3 计算模型Fig.3 Computational models

采矿平台坐标系原点位于平台的重心，坐标系和计算模型如图4所示，平台水下网格离散后网格数量为7 665个，节点数量为7 703个，对该网格划分进行了网格无关性验证。

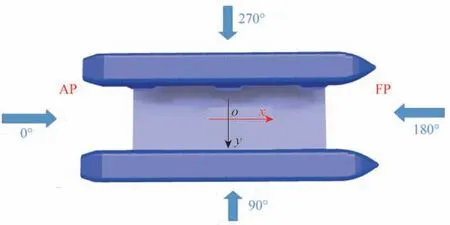
图4 深海采矿平台俯视坐标系示意Fig.4 The schematic diagram of the top coordinate system of a deep-sea mining platform

深海采矿平台的几何模型和网格模型如图5所示。

图5 平台几何模型与网格模型Fig.5 The platform geometric model and mesh model

2.2 幅频响应RAOs计算

取浪向角0°～180°，间隔30°计算幅频响应RAO（response amplitude operator）。深海采矿平台部分幅频响应曲线如图6所示。

图6 深海采矿平台RAOFig.6 Deep-sea mining platform RAO

由图6 可知：平台纵荡和纵摇运动在波浪入射角为0°时幅值最大，纵荡最大幅值为0.98 m，纵摇最大幅值为0.58°；垂荡运动在波浪入射角为90°时幅值最大，垂荡最大幅值为1.5 m；艏摇运动在波浪入射角为150°时幅值最大，最大幅值为0.27°。由水动力计算得到深海采矿平台纵摇和垂荡的固有周期分别为25.7 s 和21.2 s。

3 转场过程时域动力响应计算

针对平台转场工况，取浪向0°计算平台—输浆管—中继站一体化耦合动力响应。

3.1 转场工况海况参数

转场工况时航速为1.0 m/s，将航速转化为流速计算动力响应。转场工况的海况参数为：有效波高6.0 m；波周期11.2 s；风速17.1 m/s。

海面自然流速为1.0 m/s，沿0°方向，平台航向沿0°方向，假定平台不运动，通过流速增大模拟平台运动，则航速与自然流速叠加，海面流速为2.0 m/s。

转场工况流速：0～200 m 水深，流场为从2 m/s 减小至1 m/s 的剪切流；0.2～6.0 km 水深，流场为1.0 m/s 的均匀流。计算取风、浪、流同向。

3.2 动力定位参数整定

3.2.1 基于平台位移和推进器推力的参数整定

因为采矿平台是通过DP3 系统（dynamic position，简称DP3）控制整个采矿系统的位置，通过感知和算法，DP3调整推进器的转速和方向以控制推力，保持平台位于海上的适当位置。

深海采矿平台动力定位系统安装8 个全回转推进器，单个推进器最大输出功率4.2 MW，最大推力735 kN，推进器对称布置在左右两个下浮体上，推进器布置如图7所示。

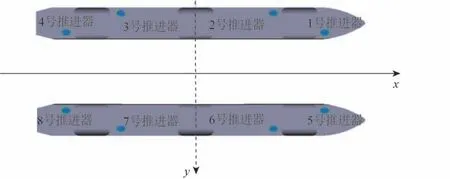
图7 深海采矿平台推进器布置Fig.7 The thruster layout of a deep sea mining platform

通过嵌入在SESAM 程序中的 SIMA 程序模块，进行参数整定［15］，SIMA 模块中应用卡尔曼（Kalman）滤波及LQ（linear quadratic method）算法，进行推力分配和优化。打开SIMA 模块中的Control System，设定控制增益和滤波增益，输入风浪流参数及水深，进行参数整定。整定过程固有周期取值区间为100～190 s，以10 s为间隔；截断周期取值区间为60～100 s，以5 s为间隔。最终得到90种参数组合进行参数整定。

以转场工况、浪向0°为条件，输入不同的参数组合和风浪流参数进行时域计算，得到不同参数组合平台水平位移和推进器推力如图8和9所示。

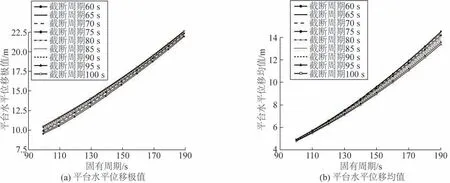
图8 平台水平位移与参数整定的关系Fig.8 Relationship between horizontal displacement of platforms and parameter setting

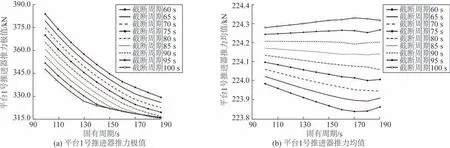
图9 平台推进器推力与参数整定的关系Fig.9 Relationship between thrust and parameter settings of platform thrusters

由图8～9可知：随固有周期的增大，平台水平位移均值和极值增大，推进器推力极值减小；随截断周期的增大，平台水平位移极值增大、均值减小，推进器推力极值减小、均值增大。所以，取转场工况0°浪向参数整定结果见表4。

表4 转场工况浪向0°参数整定结果Tab.4 Parameter setting outcomes of wave direction 0° under transition condition 单位：s

3.2.2 中继站位移和输浆管轴力与参数整定的关系

计算中继站位移和输浆管轴力与参数关系结果表明，参数整定对于输浆管单元轴力和中继站位移影响相对较小。此处略去该计算过程。故选取表4参数整定结果计算时域响应。

3.3 转场工况一体化耦合时域响应结果

按照3.2节参数整定结果，设定推进器参数，考虑转场工况浪向0°，计算图5所示模型的时域运动响应。

3.3.1 深海采矿平台时域响应结果

转场工况0°浪向采矿平台主要运动是纵荡、垂荡和纵摇时域响应，计算结果如图10所示。

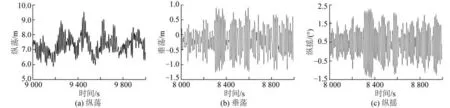
图10 平台运动时域响应结果Fig.10 Time domain response outcomes of platform motions

转场工况0°浪向平台六自由度运动统计如表5所示。

表5 转场工况浪向0°平台运动响应统计Tab.5 Statistics of wave motion response to the 0° platform under transition conditions

由表5 可知：转场工况浪向0°平台主要发生纵荡、垂荡和纵摇运动，纵荡极值为9.13 m，垂荡极值为1.44 m，纵摇极值为3.52°。

3.3.2 推进器推力时域响应结果

转场工况浪向0°，1号、4号、5号和8号推进器推力时域响应曲线如图11所示。

图11 推进器推力时域响应结果Fig.11 Time domain response outcome of thruster thrusts

转场工况浪向0°各个推进器推力统计如表6所示。

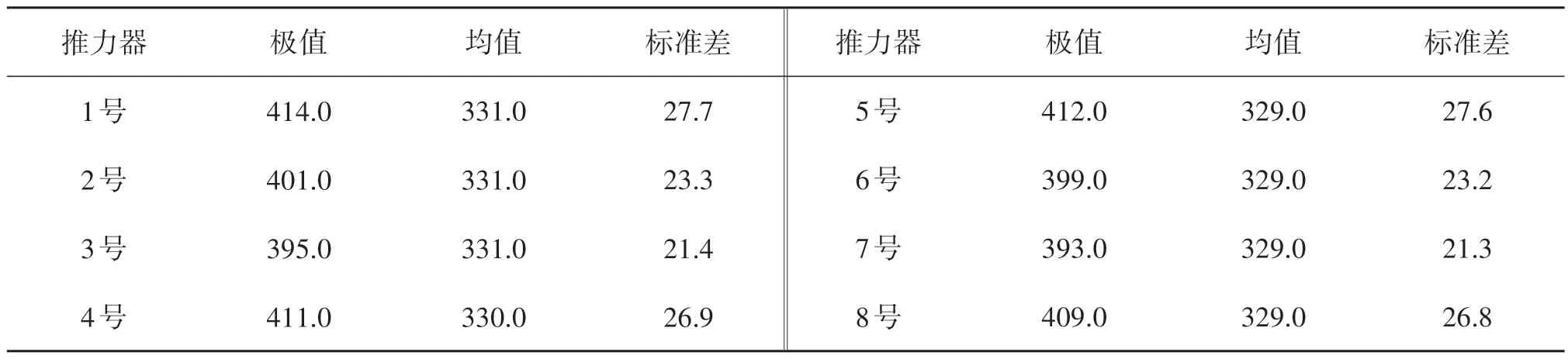
表6 转场工况浪向0°推进器推力统计Tab.6 Statistics of wave motion response to 0° platform under transition conditions 单位：kN

由表6 可知：各个推进器推力极值和均值基本一致，单个推进器可以发出的有效推力为735.0 kN，远大于控制平台运动需要的推力，推进器推力可以充分满足控制平台运动的要求。

3.3.3 输浆管轴力时域响应结果

输浆管轴力主要受钢管湿重和浮力材料的影响，浮力材料的布置导致输浆管的轴力自浮力材料布置位置的最下端开始减小。转场工况0°浪向，输浆管顶端单元、底端单元和浮力材料布置底端单元（对应389 单元）的轴力时域响应曲线如图12所示。

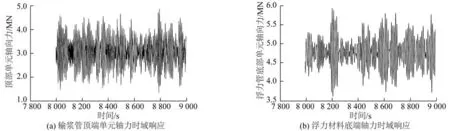
图12 输浆管转场工况轴力时域响应Fig.12 Time-domain responses of axial force of slurry conveying pipes under transition condition

转场工况浪向0°，输浆管顶部单元、底部单元和浮力材料底部单元的轴力统计如表7所示。

表7 转场工况浪向0°型单元轴力统计Tab.7 Statistics of axial force of wave direction 0° type element under the transition conditions 单位： MN

统计所有单元的轴力均值和极值，轴力的均值和极值随单元编号的变化如图13所示。由图13可知：输浆管轴力的均值和极值都自下而上先增大后减小，且在单元编号389取得最大值，此处为浮力管最下端的单元，极值为5.94 MN，该极值拉力主要由钢管重量和浮力管的重量差引起。

图13 输浆管单元轴力统计Fig.13 Axial force statistics of the slurry conveying pipe unit

3.3.4 中继站运动响应及输浆管构型

转场工况下，中继站运动响应主要是纵荡和垂荡，其横荡很小，浪向0°下中继站位移统计如表8所示。

表8 转场工况浪向0°中继站位移统计Tab.8 Statistics of wave direction 0° relay station displacement under the transition conditions 单位：m

由图14和表8可知：转场工况、0°浪向中继站主要发生纵荡和垂荡方向上的运动，中继站纵荡运动极值为200.29 m，垂荡运动极值为11.87 m。对于0°浪向，以输浆管的纵荡和垂荡为坐标点，画出输浆管的位移构型图15。

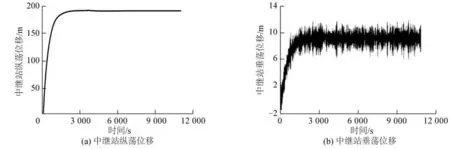
图14 中继站转场工况位移响应Fig.14 Displacement response of relay stations under the transfer condition

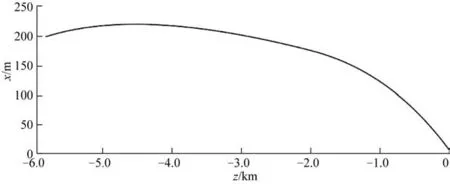
图15 转场工况浪向0°输浆管构型Fig.15 Configuration of slurry conveying pipe at 0 ° wave direction under transition conditions

4 结 语

考虑动力定位系统，建立采矿平台和水下系统一体化耦合动力响应计算模型，计算分析转场工况采矿系统的耦合动力响应，得到如下主要结论：

1）建立的平台—输浆管—中继站一体化耦合动力分析模型，可以全面研究采矿平台及水下系统的动力响应特性，对深海采矿设施的动力分析具有指导意义。

2）中继站纵荡运动极值为200.29 m，其他方向运动相对很小，深海采矿平台设计过程应该设法降低中继站运动；此外，中继站的运动对输浆管强度影响较大。

3）输浆管最大轴力出现在浮力材料的底端，为5.94 MN，位于水下2.0 km。后续研究应改变浮力材料的位置，使轴力最大值出现在输浆管的顶端，并且适当减小轴力，提高输浆管的疲劳强度。