深海浮球内部气压对水下内爆波的抑制机理

2024-03-12赵一凡胡延东冯淼林

海洋工程 2024年1期

赵一凡，赵敏，胡延东，冯淼林

（1.上海交通大学海洋工程国家重点实验室，上海 200240；2.上海交通大学船舶海洋与建筑工程学院，上海 200240；3.上海交通大学高新船舶与深海开发装备协同创新中心，上海 200240）

地球最深处的海沟——马里亚纳海沟深度接近11 km，深海潜器在万米深海下需要承受高达114 MPa的压强，面临着非常大的内爆风险。目前深海潜器耐压结构主要采用钛合金，而潜器需使用浮力材料微珠复合泡沫材料［1］等为潜器提供浮力，但是使用时会增加潜器的质量和成本［2］。与一般材料相比，陶瓷材料具有比强度高、耐腐蚀、密度小等优点。2009 年美国研制的“海神”号潜器首次使用陶瓷空心浮力球作为浮力设备，潜器成功下潜到马里亚纳海沟底部［3］。然而，由于陶瓷的脆性及难以避免的微小缺陷降低了其在高压环境下的安全性，2014 年“海神”号在探索克马德克海沟下潜到9.9 km 左右发生内爆事故，导致整个潜器成为碎片［4-5］。

内爆的发生会造成非常严重的后果，所以减弱或抑制内爆波非常有必要。Gupta等［6］在半封闭圆管内放置了2 个中空圆柱体，当其中一个内爆引发殉爆时，由两者内爆引起反向的水锤波发生叠加，使循环压力载荷大大降低。目前工程中的方法主要有两种：一是在结构外侧添加保护罩，如Ling等［7］使用保护罩来对PMT进行保护，达到了很好的抑爆效果，但是保护罩减弱了PMT 的透光性，也使得结构更加笨重；二是在内部增加填充物来达到减弱内爆波强度的效果。Vanzant等［8］内爆了27个不同直径下分别在内部填充真空、1大气压空气和聚苯乙烯泡沫塑料小球的铝制球壳并将测量的正负压力脉冲与气泡溃灭理论进行比较，但是并没有指出不同内部填充对压力脉冲的影响。Cor和Miller［9-10］通过解析的方式验证了气泡中内置结构能有效减小内爆过程中释放到周围环境中的冲击能量。Javier等［11］在圆柱管中增加了泡沫，达到了很好的抑制效果。增加内部气体的初始压力或者改变气体成分可以视作在内部增加填充物，但是对于内部气体的影响，出现了两种不同的说法。Gish［12］从能量角度出发，提出增加内部空气的初始压力或者使用惰性气体替代空气，可以增加压缩气体所需的能量，从而达到抑爆的效果。Morenko［13-16］以Turner［17］的试验为基础，做了一系列纯流体的计算流体力学数值模拟，得到了在环境压力不变的前提下，增加球体内部气压能有效降低内爆强度的结论。Moezzi-Rafie和Nasiri［18］进行了微气泡内爆的纯流体模拟，指出球体内部气体密度越大，内爆强度越弱。杜志鹏等［19］借鉴水下爆炸气泡动力学理论，基于能量守恒原理推导了一种不可压缩流体中球型内爆理论模型，定性探究了内爆冲击波与球形尺寸、静水压、内部气体初始压力等参量的关系，指出不同的内部压力对压力波的峰值不产生影响。Qu 和Zhou［20］通过ABAQUS 的CEL 方法，对不同空气内压的铝管内爆进行了模拟，指出改变内部压力会影响内爆能量，但是对压力峰值几乎没有影响。

为了确定内部气体的初始压力增加是否能够减弱陶瓷球壳内爆的内爆波，下文首先使用气泡动力学对气—水两相流体模型，理论分析了增加气体初始压力对内爆压力波的抑制机理；之后，考虑到实际浮球内爆的复杂性，利用Hu等［21］建立的气—固—水三相流固耦合模型模拟了两端挤压球壳引起的内爆，模型考虑了高压水和空气的可压缩性以及球壳破碎的影响，得到了更为准确的结果。

1 理论模型和有限元模型

1.1 气泡动力学模型

气泡动力学模型可以从理论上分析一个气泡在静水压力下的动态响应。是一个经过简化的一维、气—水两相理论模型。

假设在静水压力为p0的无限大水域中存在一个压力为pg0且初始半径为r的气泡，令平衡时的气泡半径为R0。当忽略表面张力，且气泡以理想球形收缩和扩张时，可根据Keller-Miksis 方程［22-23］得到气泡的运动方程：

式中：R为任意时刻气泡半径；Ṙ和R̈分别为任意时刻半径对时间的导数和二阶导数；cL为水中声速；ρL为水的密度；γ为气体的比热参数。此式为非线性常微分方程，可使用龙格库塔法求解得到气泡半径的动态响应R（t）。

假设气泡外的水为无旋不可压缩流体，根据势流理论和Bernoulli 方程［19］可以得到任意一点的压力峰值预测公式：

其中，d为探测点到球心距离。将气泡运动方程求解得到的R（t）代入式（2），就可以得到任意一点的压力随时间变化曲线。但是式（2）没有考虑水的可压缩性，在气泡压缩至最小时内部压力达到最大值，水锤效应导致气泡反向向外压水，水中的压力则因不可压假设刚性的向外传递，而高估水中的压力波峰值。

定义压力脉冲（表压）为压力波峰值减去环境压力。当压力达到峰值时，气泡半径达到最小Rmin，即此时Ṙ= 0，压力脉冲的计算公式可以简化为：

将探测点到球心距离与初始半径的比值记为无量纲探测距离：

使用无量纲探测距离R*来表示，式（3）可以改为：

理论分析表明，在考虑波的传播介质是无旋且不可压缩水时，通过气泡动力学模型可以得到压力脉冲随至球心的距离以指数-1衰减。

1.2 ABAQUS有限元模型

有限元模型可以模拟气—水两相的气泡在深海中的动态响应，更可以模拟壳体因两端碰撞导致破碎的内爆过程，即采用气—固—水三相流固耦合模型，结合陶瓷的脆性失效准则，得到更为接近实际现象的结果，接下来着重介绍三相流固耦合模型。

深海浮球外径91 mm，壁厚1.5 mm，材料为99.9%Al2O3陶瓷，由DeepSea Power & Light 公司制作，可以承受万米水深下114 MPa的压强。计算参数采用已经报道的试验得到的Al2O3陶瓷特性的下限值，即弹性模量E=360 GPa，泊松比为0.23，抗弯强度为310 MPa，密度为3 800 kg/m3［24-25］。

为了校核内侧高压的浮球在外侧常压状态下是否存在向外的破裂风险，使用材料力学方法，假设截面上的拉应力均匀分布，可推导内侧高压的球壳承受的最大拉应力为：

因此，内部可施加的压力为：

式中：R1和R2分别为球壳外径和内径；pg为内部气压；S为安全系数。取安全系数S=2［26］，代入数据得到最大安全内压为10.8 MPa。使用ABAQUS计算1 MPa内压时，球壳的最大应力为14.6 MPa；由上述公式得到的球壳最大拉应力为14.4 MPa：两者非常接近。综上所述，内部初始气压为1 MPa的陶瓷浮球在空气中不会被破坏，且有较高的安全余量。

陶瓷球壳制作可分为陶瓷半球壳制作成型和两个半球壳合封2 个过程［27］。本项目中的球壳，可在陶瓷半球壳制作成型后，将合封处理过程于1 MPa高压仓中进行，即可以得到内部高压的陶瓷球壳。

三相流固耦合模型使用了CEL 方法（coupled eulerian-lagrangian）。CEL 方法包含2 个显式求解器：欧拉流体求解器（求解N-S方程）和拉格朗日有限元求解器（求解材料应力、应变、变形、位移、速度和加速度）。欧拉流体通过接触面与拉格朗日材料相互传递网格的位移、速度和接触压力等信息。图1 为有限元模型的八分之七示意图。固体区域陶瓷球结构，使用六面体拉格朗日网格（C3D8R）。固体材料固定在拉格朗日网格上，在模拟过程中随拉格朗日网格一起移动。氧化铝陶瓷使用脆性断裂准则，即当最大主应力达到310 MPa后从球壳单元中删除。欧拉域半径为球壳半径的20 倍，包含了海水和空气两相，使用六面体欧拉网格（EC3D8R），基于多相流计算的VOF 方法对海水—空气界面进行跟踪。欧拉流体通过状态方程考虑空气和水的压缩性。分别使用理想气体状态方程和刚性气体状态方程表示空气和水的可压缩性：

图1 流固耦合有限元模型解剖示意Fig.1 Finite element model of fluid-structure interaction

式中：Pa和Pw分别表示空气和水的压强；ea和ew分别表示空气和水的比内能；γa=1.4 是空气的比热；γw=4.4 是水的经验常数；Pref=600 MPa 为取决于分子间作用力的常数。假定内爆是绝热过程，内能的增加只由流体压力所做的机械功引起。在欧拉域的外边界上采用自由流入和非反射流出边界条件。

1.3 有限元解的网格无关性分析

有限元解的网格无关性验证分为欧拉（流体）网格和拉格朗日（固体）网格两步进行。

首先，流体域欧拉网格无关性解的验证使用气—水两相流体模型模拟了气泡运动的过程，将求得的气泡半径与理论模型结果进行了对比，如表1所示。计算发现，总网格数为948 672个（水域含855 360个，空气域含93 312个）时和理论吻合较好。空气域网格尺寸为2 mm，水域网格沿球面均布，沿径向尺寸由内向外逐渐变疏，为2～20 mm。

表1 两相有限元模型和理论模型气泡半径随时间变化对比Tab.1 Comparison of bubble radius between the two phase finite element model and the theoretical model

其次，进行固体域拉格朗日网格无关性解的验证。欧拉网格采用前述网格，加入固体球壳。球壳表面使用均匀网格，厚度方向采用多层网格。模拟发现，厚度方向采用2层网格模拟的球壳的破坏与试验碎片的破坏情况相近。改变球壳网格密度，不同测点的内爆脉冲差异很小，如表2 所示。因此，下文采用中等密度的拉格朗日网格（网格数为15 552）进行计算。

表2 三相流固耦合模型不同网格疏密下R*=1处压力脉冲对比Tab.2 Comparison of pressure pulse at R*=1 in three-phase fluid-structure interaction model with different mesh densities

2 气泡动力学模型定性分析内部气压的影响

2.1 气泡动力学理论分析

由式（1）得到气泡在水压作用下半径随时间的变化，如图2 所示。当气体的初始内压增大时，气泡压缩的速度并没有明显差别；但是当内压增大时，相同体积下包含空气的物质的量增多，气泡的压缩更困难，能达到的最小半径和内外压趋于平衡时半径都会增大，在达到最小半径后的振荡也更为明显。1 MPa 初始内压的气泡半径可最小压缩至6.24 mm，是0.1 MPa 初始内压气泡最小半径2.62 mm 的238%，可见内压的增加对气泡的塌缩具有明显的抑制作用。

2.2 气泡动力学模型能量分析

利用气泡动力学模型对气泡在高压海水中的能量变化进行分析［12］，整个过程的海水静压做功为：

式中：W是海水静压所作的总功；ΔV是气泡减小的体积。气泡动力学模型忽略了陶瓷壳变形和破坏需要消耗的能量。海水静压所作的功可以分为2个部分：一部分用于压缩空气；另一部分以压力波的形式释放到水中，引起水的流动和压力升高。压缩空气的能量可以表示为：

式中：V0是气泡的初始体积；V是气泡变化后的体积。气泡压缩至最小时的总能量直接影响了压力脉冲的大小，表3 是气泡压缩至最小时3 种不同内压下各部分能量的计算结果。从表3 中可以看出，内压的增加使得整个系统的总能量略有下降，却可以显著提高压缩空气所需的能量。内压从0.1 MPa 提高至1 MPa 时，压缩空气的能量提高了6.8 kJ，压缩空气的能量占总能量的百分比由6.5%提高至21.7%。可以看出，海水静压所做的功大部分释放到海水中以压力波的形式释放，然而提高初始空气的压力可有效增加压缩空气所需的能量，从而显著降低水中压力波峰值。

表3 气泡压缩过程的能量转化Tab.3 Energy conversion during bubble compression

3 陶瓷浮球内爆的三相流固耦合模拟

3.1 陶瓷浮球内爆过程

陶瓷浮球可承受万米水深下114 MPa 压强。因此，浮球的内爆需要施加两侧集中力（或碰撞）来启动。针对内部气压从0.001～1 MPa 的陶瓷浮球因挤压（挤压方向沿X方向）导致的内爆过程进行了模拟。图3 为内爆发生后球壳破碎和气体塌缩的过程，以0.1 MPa 内部气压为例，不同内压时的内爆过程相似。如图3 所示：0.020 ms 时球壳从挤压的两侧产生破洞，球壳的破碎由两侧向中间发展，在0.028 ms 时球壳接近完全破碎，这个过程仅用时0.008 ms；气体在球壳开始破碎后接触外界高压水则向内塌缩，球壳在X方向受压产生破洞处，先行产生水向内的射流，造成内部气体非球形的塌缩；未破碎的球壳部分阻挡了水的进入，导致垂直于X方向的气泡压缩程度较弱；内部气体的塌缩过程较球壳破碎的过程要缓慢很多，气体在0.142 ms时达到最小状态。受到球壳破碎过程的影响，气体产生非球形的塌缩，也使得后续的内爆波存在方向性差异。

图3 两侧挤压破坏和内部气体塌缩过程（初始内压为0.1 MPa）Fig.3 Ceramic fracture caused by squeeze and internal gas collapse process (the initial internal pressure is 0.1 MPa)

为了观察内爆发生后在水中某点压力随时间的变化，在挤压方向（X方向）和垂直于挤压的方向（Z方向）分别设置了10 个探测点（至球心距离分别为1～10 倍球壳半径）。图4 为0.1 MPa 初始气压内爆时X方向10个测试点压力随时间的变化曲线，Z方向测试点压力变化类似。球壳和内部气泡首先受压变小，周围水中压力降低；随后水向球壳内部涌入，在气泡压至最小体积时产生水锤效应；接着，气体膨胀反向对水做功，在水中产生向外传播的压力波。图4 表明，压力波峰值随距离的增加迅速衰减，且峰值尖锐程度降低。这说明，深水内爆过程中水的可压缩性不能忽略，它产生压力波的扩散，一定程度上起到抹平压力波峰值的作用。

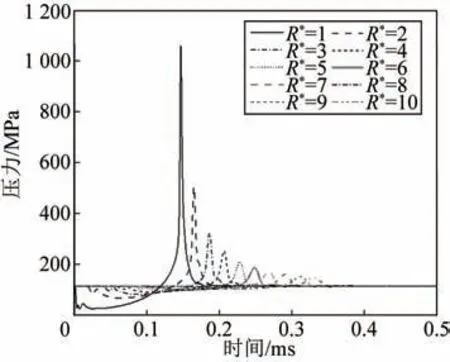
图4 X方向多测点压力的时间历程（初始内压为0.1 MPa）Fig.4 Temporal pressure profile in the X-direction for test points (the initial internal pressure is 0.1 MPa)

3.2 球壳内部气压对内爆波峰值的影响

图5 显示了0.001、0.1 和1 MPa 内压情况下发生内爆时气体体积的变化情况。从图5 中可以看出：内爆开始后，3 种不同内压下的气体均开始向内收缩，并没有明显的不同；随着时间的推进，在0.14 ms 左右气泡被压缩至最小时的状态已经有所区别，其初始压力越大，最小体积越大，气体越难压缩；后续波动和理论模型相近，内压越大时振荡越明显。在0.20 ms时，0.001 MPa的气泡仍然十分破碎，而1 MPa的气泡呈现饼状。理论模型中，1 MPa气体的最小体积与0.1 MPa气体最小体积相比超过8倍；但是在有限元模型中，由于射流影响，气体被分散压缩（非球形压缩），不同气压的最小体积差别没有理论模型中显著。

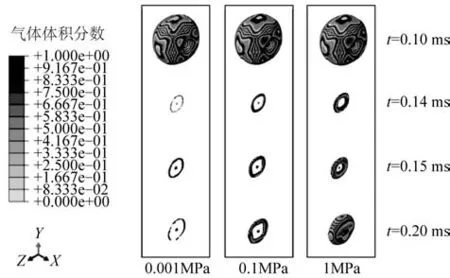
图5 不同初始气压气体体积随时间的变化Fig.5 The change in volume of gas with time at different initial internal pressures

气体塌缩过程的方向性差异导致了内爆波的方向性差异，0.1 MPa 初始气压内爆过程中0.15 ms 时水中的压力分布如图6所示，此时内爆波传播至R*=1附近。X方向的水锤效应和气体膨胀更为强烈，产生内爆波呈椭球形，压力脉冲高于Z方向，而到达时间略晚。

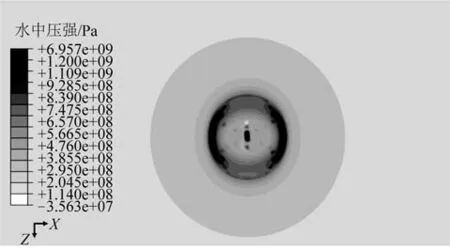
图6 压力波传播的方向性Fig.6 Directional propagation of the pressure wave

表4 为不同内部初始气压在无量纲距离R*=1 处得到的压力脉冲的比较。从表4 可以看出，增加内部气体初始压力可以降低各个方向上压力脉冲。与0.1 MPa初始气压的情况相比，1 MPa的空气可以使X方向的压力脉冲下降24.8%，Z方向的压力脉冲下降15.6%，有效地减弱了内爆波峰值，而整体浮球质量只增加了高压气体的质量，几乎可以忽略。

表4 不同初始气压产生的压力脉冲（R*=1测试点）Tab.4 Comparison of pressure pulse at R*=1 produced by implosions with different initial internal pressure

从表4中不同方向上的压力脉冲可以看出，增加初始气压对压力脉冲较高处（X方向）抑制效果更明显。因此，随着内压增高，内爆的方向性差异受到削弱。例如，内压由0.1 MPa 增加至1 MPa 时，Z方向和X方向压力脉冲之比由0.58 增加至0.65。内爆的方向性差异受到削弱意味着内爆能量均匀向外释放，减轻了球壳随机碰撞导致内爆能量在某方向集中释放带来的严重后果。

3.3 球壳内部气压对内爆压力波衰减系数的影响

图7显示了X方向各点压力脉冲（表压）随距离的增加而呈指数型衰减。对应不同内部气压的拟合曲线分别为：

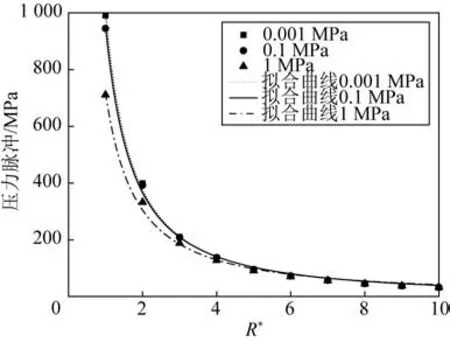
图7 X方向不同初始气压压力脉冲随距离增加的衰减Fig.7 Decay of pressure pulse in the X-direction with increasing distance for different initial internal pressures

在理论模型中，压力脉冲值随距离衰减的指数为-1，见式（5）。在实际深海环境中，水的压缩性不可忽略，脉冲衰减速度比理想情况下要快，式（12）～（14）中衰减指数均小于-1。由图7也可看出：增加内压显著降低了球壳附近水中的内爆脉冲值；随着距离的增加，增加内压对于内爆压力脉冲的影响越来越小，在R*=4之后，曲线几乎完全重合。因此，增加内压至1 MPa 可以有效降低近端内爆压力，一定程度上抑制殉爆的发生。