基于堆叠稀疏判别自编码的滚动轴承智能故障诊断方法

曾梦洁,李舜酩,2,李冉冉,李家诚,徐坤

(1.南京航空航天大学 能源与动力学院,南京 210016;2.南通理工学院 汽车工程学院,江苏 南通 226002;3.西北工业大学 无人系统技术研究所,西安 710072)

作为旋转机械的关键部件,滚动轴承的运行状态对机械的健康运转具有重要影响。 为减小机械故障维护成本和不必要的设备损耗,研究滚动轴承的故障诊断方法十分必要[1]。传统故障诊断方法主要是基于振动信号的处理分析,随着智能诊断方法的发展,深度学习成为故障诊断应用的研究方向。深层网络相比于浅层网络能够取得更好的诊断结果:文献[2]提出了基于多传感器信息融合的轴承故障诊断模型,采用一维卷积神经网络(1DCNN)对某航空发动机轴承故障振动数据进行特征提取与分类,获得了比其他浅层网络更优的诊断性能:文献[3]提出了一种基于循环神经网络的时变工况下轴承智能故障诊断框架,利用长短期记忆(LSTM)网络存储和传输分类信息,同样获得了优于传统神经网络故障诊断方法的结果。

深度学习模型是由数据驱动的模型,能够自动标记数据并学习数据特征。简单的有监督模型易受数据输入和参数调整的影响,无监督模型则具有良好的特征挖掘能力,常用于特征提取和数据聚类。自编码网络(Auto Encoder,AE)是无监督模型中的典型方法,已经广泛应用于各种领域,由于自编码的结构特性而能够在无需标签的情况下对数据规律进行深入分解并实现特征提取和数据降维。文献[4]提出了一种批量归一化自编码器的新网络用于滚动轴承智能故障诊断,能够在轴承原始振动信号中提取显著特征并解决转速波动下的故障诊断问题。文献[5]开发了一种称为变体稀疏过滤的无监督稀疏特征学习方法,能够学习具有最佳稀疏分布的特征,准确识别滚动轴承单一故障和复合故障。

尽管无监督学习在数据特征提取方面具有良好的发挥,但所提取特征未必是有利于分类的特征。为增强模型性能,将有监督模型特点与无监督模型特点相结合的半监督模型获得了青睐:文献[6]提出了一种分层稀疏人工神经网络,将动态时间窗口与堆叠稀疏自编码相结合构建了动态稀疏堆叠自动编码器 (DSSAE)并对动态故障数据进行分类,仿真表明DSSAE的性能优于稀疏自编码和堆叠稀疏自编码;文献[7]提出了一种增强深度自编码网络,采用最大相关熵代替均方误差作为自编码器的损失函数,加入稀疏惩罚项和嵌入非负约束因子的收缩惩罚项进一步减小重构误差,通过灰狼优化算法自适应地选取网络关键参数,试验结果表明该方法具有更强的特征提取能力与稳定性,对变工况下的轴承振动数据也能达到较高的识别精度;文献[8]针对旋转机械传感器信号样本有限从而影响深层网络模型训练学习的问题,提出一种结合改进残差自编码网络与类自适应方法的故障诊断模型以应对小样本数据,结果表明该模型能够在微量标记振动数据的不同工况下有效提高故障诊断准确率。

在现有研究中,较少学者针对数据类的结构特性展开分析,而关注数据的结构特性能够增加特征差异并提高分类性能。文献[9]提出了一种基于保留局部和全局特征结构的堆叠稀疏自编码用于故障检测,能够使数据尽可能地保留结构特征但并未从特征差异化角度考虑数据分类;文献[10]提出了一种新的半监督自动编码器(判别式自动编码器)提取特征并用于故障诊断,通过最大化来自不同类别的样本中心之间的距离,判别式自动编码器能够为最终诊断提取更多有用的表示,但该方法未考虑数据的结构特性;文献[11]提出了一种用于滚动轴承故障诊断的特征距离堆栈自动编码器(FDSAE),具有比现有方法更强的特征提取能力和更快的网络收敛速度,但由于距离惩罚项的限制,该方法的泛化性较差:上述方法从不同角度考虑了数据的结构特性,从数据结构层面增强了自编码网络的性能,但仍存在一定的局限性,针对不同的应用场景仍有改进空间。

为增强自编码方法的特征提取能力和诊断稳定性,本文结合稀疏自编码(Sparse AE,SAE)的特性构建堆叠稀疏自编码(Stacked SAE,SSAE),利用KL散度约束深层网络神经元稀疏激活度以防止网络过拟合,结合半监督机制改进传统网络并利用标签信息微调提升模型分类性能,在上述基础上充分考虑数据类的结构特性,提出一种堆叠稀疏判别自编码(Stacked Sparse Discriminative Autoencoders,SSDAE)智能故障诊断算法,从类几何特征和类数据特征2个角度出发充分发掘数据的深层规律,以解决复杂工况下滚动轴承故障诊断结果不理想的问题,实现可靠的滚动轴承智能故障诊断。

1 堆叠稀疏自编码基本理论

自编码网络是一种3层无监督神经网络模型,最大特点是令输出y等于输入x,利用网络编码层和解码层实现对输入信号的重构,寻找能够简要表示原始数据的深层规律。AE模型结构如图1所示。

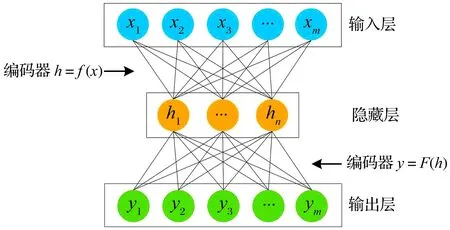
图1 AE模型结构图

将预处理后的信号数据输入已经建立的AE模型中,通过隐藏层的编码函数(一般选用Sigmoid函数)对输入数据x进行编码处理,获取与隐藏层节点维数一致的简化特征向量,即将原始m维数据映射至隐藏层的n维向量;再通过隐藏层的解码函数(一般选用Sigmoid函数)对简化特征向量进行解码处理,实现对原始数据的重构,即将n维简化特征向量映射至输出层的m维数据y。当批样本数为N时,其重构误差为

(1)

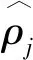
(2)

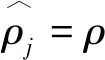
(3)

(4)

式中:N为批样本数;n为隐藏层中神经元的个数;β为稀疏权重因子。

SAE能够很好地实现数据降维和特征提取,但仅采用单层隐藏层时数据重构能力存在较大限制,往往难以提取特征复杂数据更核心的特征规律。堆叠稀疏自编码网络通过堆叠连接多个SAE结构,逐层分析原始数据的深层特征,多个隐藏层能够层次性的提取数据规律,增强自编码网络的特征提取能力。传统SSAE模型的损失函数为

(5)

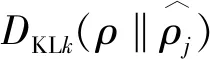
尽管SSAE与SAE的损失函数差异不大,但深层网络能够比单层网络提取更多的特征。另外,SSAE的多层稀疏激活度约束能够充分利用SAE的特性去除高维干扰而提取低维特征,增强自编码网络的鲁棒性[12]。3层的传统SSAE网络如图2所示,利用上一层隐藏层的输出训练下一层SAE,并将最后一层的简化特征向量通过Softmax函数进行分类,可验证网络的有效性[13]。

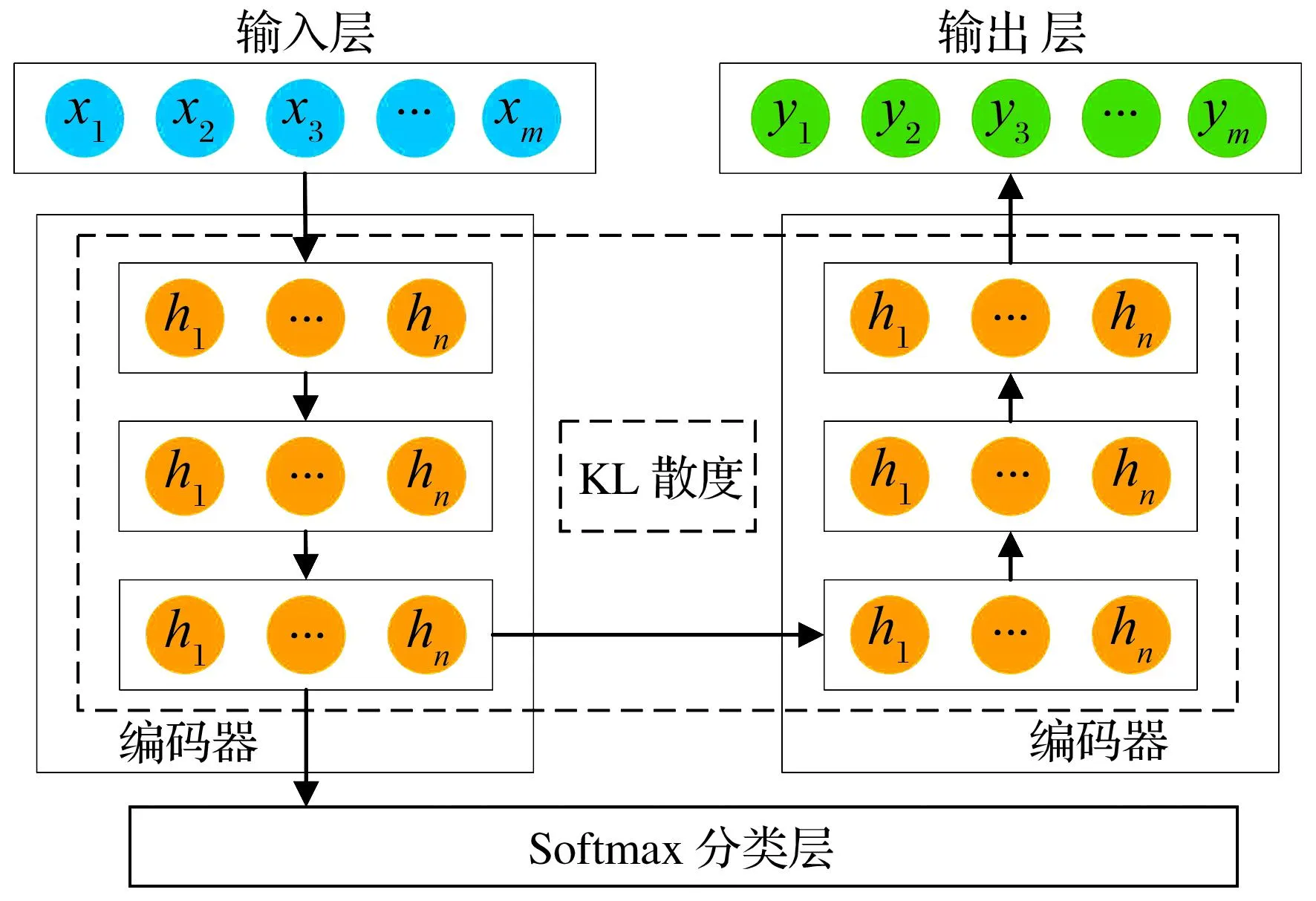
图2 SSAE模型结构图

2 堆叠稀疏判别自编码方法

2.1 半监督堆叠稀疏自编码

为增强无监督模型的分类能力,引入半监督学习模式改进传统的堆叠稀疏自编码网络。半监督堆叠稀疏自编码(Semi-supervised SSAE,SesSSAE)借助深层的编码器和解码器无监督的对数据信息进行重构,同时利用KL散度限制深层隐藏层神经元的稀疏激活度,最后采用交叉熵进行有监督限制,对最后一层隐藏层(即特征层)进行分类调整,以完成特征提取和分类的功能。交叉熵函数ECE和SesSSAE的损失函数为

(6)

(7)

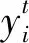
SesSSAE充分利用无监督的学习优势,在训练过程中添加标签信息,采用交叉熵函数作为有监督惩罚项,实现对原有神经网络的分类性能调整,从而提高自编码网络的特征提取能力和数据分类性能,增强智能故障诊断算法的准确性和泛化性。

2.2 样本结构特征约束

由于神经网络的黑匣子特性,尽管其拥有强大的特征提取能力,但神经网络所提取特征的含义仍未有明确解释。为增强自编码网络所提取特征的可解释性以及有效性,本文采用样本结构特征约束对网络特征重构过程进行约束。样本结构特征约束主要分为类几何特征约束和类数据特征约束2个方面:类几何特征约束主要从数据可视化角度增强数据特征差异,类数据特征约束主要从数据结构角度保留原有数据结构特征。

类几何特征主要指数据点在平面上的几何特性。将样本数据降至二维并将其以散点形式可视化于平面上,能够清晰地看出数据的类内聚合性和类间分离性,概括称为类几何特征。为量化数据的类几何特征,引入如图3所示的拟合圆测量法。

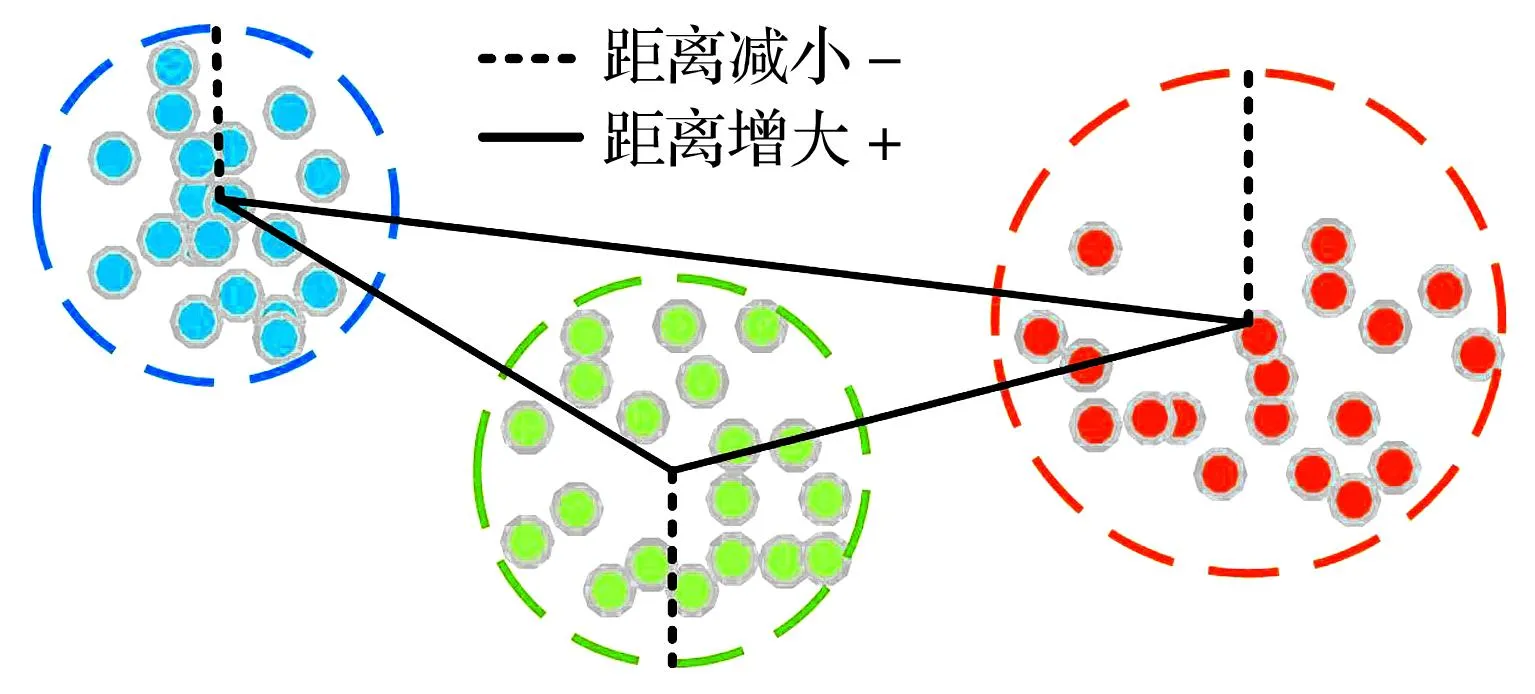
图3 拟合圆测量法

对于任意在二维平面的一簇散点,都存在一个可以将这簇散点全部围住的半径最小的圆,这个圆可以近似描述所包围散点的特征,称为拟合圆。通过拟合圆的半径近似衡量类内半径,通过拟合圆圆心之间的距离近似衡量类间距离,依据这一思想,假定有M个类,第i类有Nci组数据di,则第i类的类拟合中心点δi与类半径ri的定义为

(8)

(9)

与此同时,当共有M个类时,类内聚合半径Rc与类间聚合距离Dc分别定义为

(10)

(11)

为更好地衡量数据的类几何特性,构造类几何特征的惩罚项Lcg作为损失函数的一部分,以此约束特征重构方向,即

Lcg=Rc/Dc。

(12)

与类几何特征不同,类数据特征主要考虑数据原本的结构特性,希望尽量保留数据原有的结构信息。方差是衡量数据信息结构的主要指标,能够反映样本在数据层面的差异性。对于存在的Ns组样本x,方差S(x)可以表示为

(13)

类数据特征分为类内数据特征和全局数据特征。类内数据特征对每个类的原始样本和重构样本的方差进行差异衡量,保证网络对不同故障种类的重构适应性。全局数据特征对全部样本数据与全部重构特征的方差进行差异限制,保证训练过程整个网络的重构稳定性。假设N组样本中共有M个类,第i类有Nci组数据di,类内数据特征和全局数据特征分别表示为

(14)

(15)

式中:f(·)为对样本数据取特征层特征;xi为N组样本中的第i组样本数据。

通过方差范数对全局样本的重构数据进行约束,保证网络特征重构的稳定性和方向性。类数据特征在损失函数中的惩罚项Lcd为

Lcd=Fc+Fg,

(16)

样本结构特征约束从特征可解释性和有效性角度出发,在几何角度和数据角度约束特征的重构方向,增强自编码网络所提取的特征的可靠性和分类性。因此,样本结构特征惩罚项的损失函数Lc为

Lc=μ1Lcg+μ2Lcd,

(17)

式中:μ1,μ2分别为几何权重因子和数据权重因子。

2.3 基于SSDAE的滚动轴承故障诊断

为解决复杂工况下旋转部件故障诊断精度不理想、稳定性差的问题,本文提出主要由SesSSAE结构和样本结构特征约束组成的SSDAE智能故障诊断方法,其完整结构如图4所示:首先,基于传统SSAE模型,引入半监督训练机制利用标签信息对特征分类结果进行微调,弥补无监督机制的缺陷;然后,结合样本结构特征约束,从类几何特征和类数据特征角度对网络训练过程进行约束,限定重构特征的重构方向,在保证重构数据完整性的同时增强特征差异;最后,将提取的特征经过Softmax分类器进行分类并输出故障诊断结果。

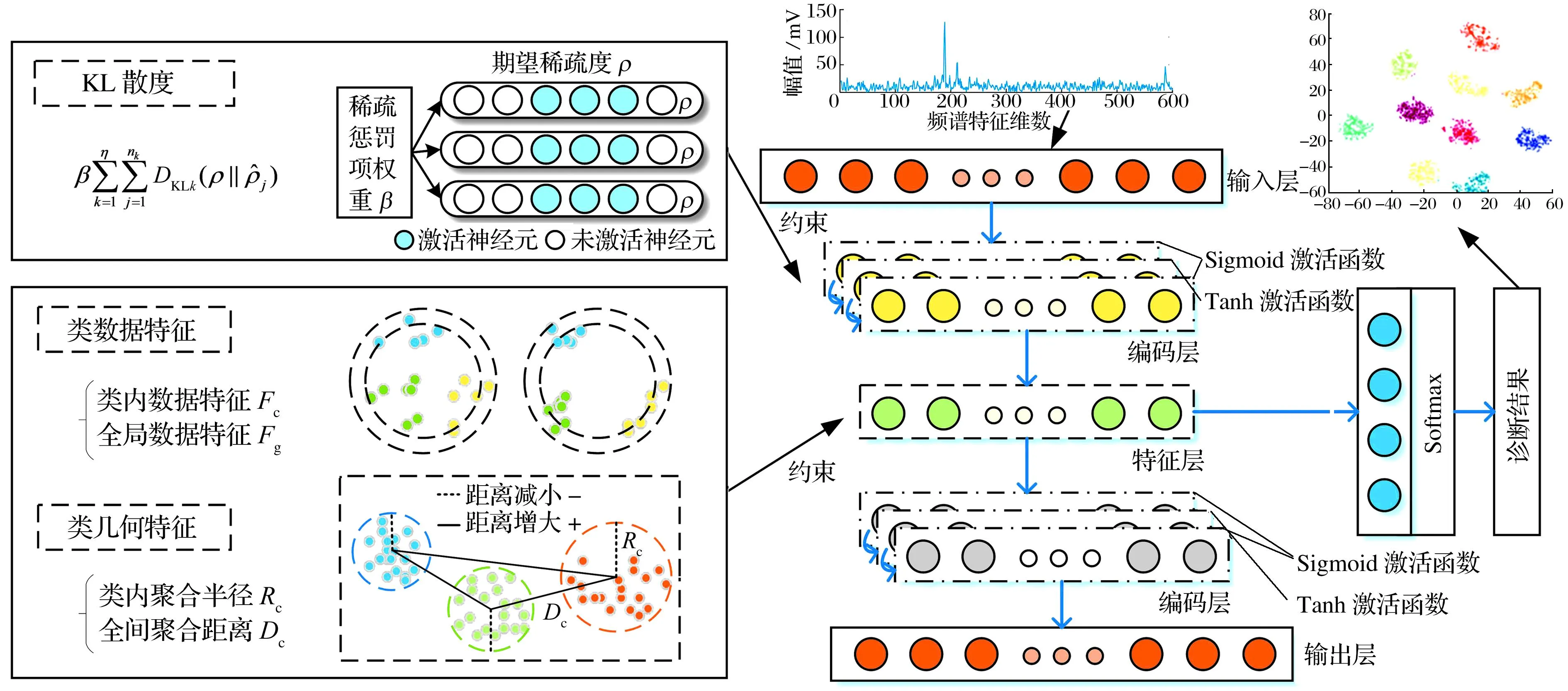
图4 堆叠稀疏判别自编码框架图

SSDAE智能故障诊断方法的详细参数见表1,其完整损失函数为

(18)

表1 SSDAE模型具体参数

SSDAE智能故障诊断方法的流程如图5所示,主要诊断步骤如下:

1)采集振动数据,利用数据增强的方式获取样本,将时域信号转换为频域信号。

2)将获取的样本划分成训练集和测试集。

3)网络参数初始化,设定关键超参数,如网络层数、神经元个数、迭代步数、批大小等。

4)将训练集输入至SSDAE网络中进行批训练,计算损失函数值,由梯度下降法迭代更新网络权重。

5)当满足阈值停止迭代,保存网络参数。

6)将测试集输入训练完成的SSDAE模型中进行测试,进行故障诊断和故障识别。

3 试验验证

3.1 数据集描述

选取美国凯斯西储大学(CWRU)的滚动轴承数据集进行SSDAE算法验证,试验轴承型号为SKF 6205,选择采样频率48 kHz的驱动端信号作为试验数据,样本集的详细划分见表2,样本集A/B/C/D均包括4个工况(0,1,2,3 HP分别对应1 797,1 772,1 750,1 730 r/min)下各10种轴承故障类型,每种故障各600组样本。采用小样本长度重叠采样的数据增强模式以增加样本数量,每组样本的长度均为600,随机抽取25%的样本作为测试集,余下划分为训练集。

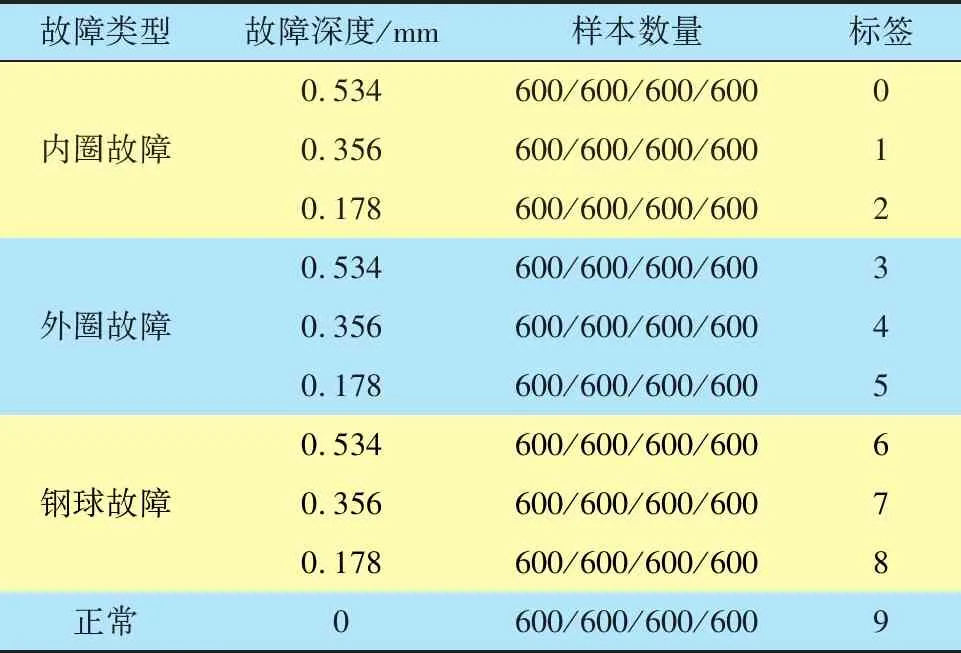
表2 CWRU样本集A/B/C/D的详细划分

3.2 样本结构特征约束验证

采用t-SNE降维可视化方法对提取的特征层进行降维分析,直观地对比不同约束条件下所提取的特征,从而验证本文所提样本结构特征约束的有效性。在参数相同的情况下,选择以下4种方法进行对比分析:1)本文所提SSDAE;2)SSDAE_NOLc,在本文所提方法的基础上去掉样本结构特征的约束项;3)SSDAE_NOLcg,在本文所提方法的基础上去掉类几何特征的约束项;4)SSDAE_NOLcd,在本文所提方法的基础上去掉类数据特征的约束项。

4种方法在样本集B测试集上的特征层的t-SNE可视化结果如图6所示:1)在没有类几何特征约束的情况下(图6a),尽管在类数据特征影响下各类别的聚拢性较好,但各类间的差异较大,类分离性仍有增强的空间;2)在没有类数据特征约束的情况下(图6b),数据的类间分布相对均匀,但各类内部的数据分布较为分散,体现了类几何特征对数据类内分布间距的约束作用;3)对比图7c和图7d可知,有样本结构特征约束情况下(图6d),各类在二维平面上的数据分布变得更加均匀分散,增强了不同故障特征的差异性,对于单组类别,图6d的类别更加的紧凑,散点分布较为匀称,证明所提SSDAE方法具有良好的特征提取性能。

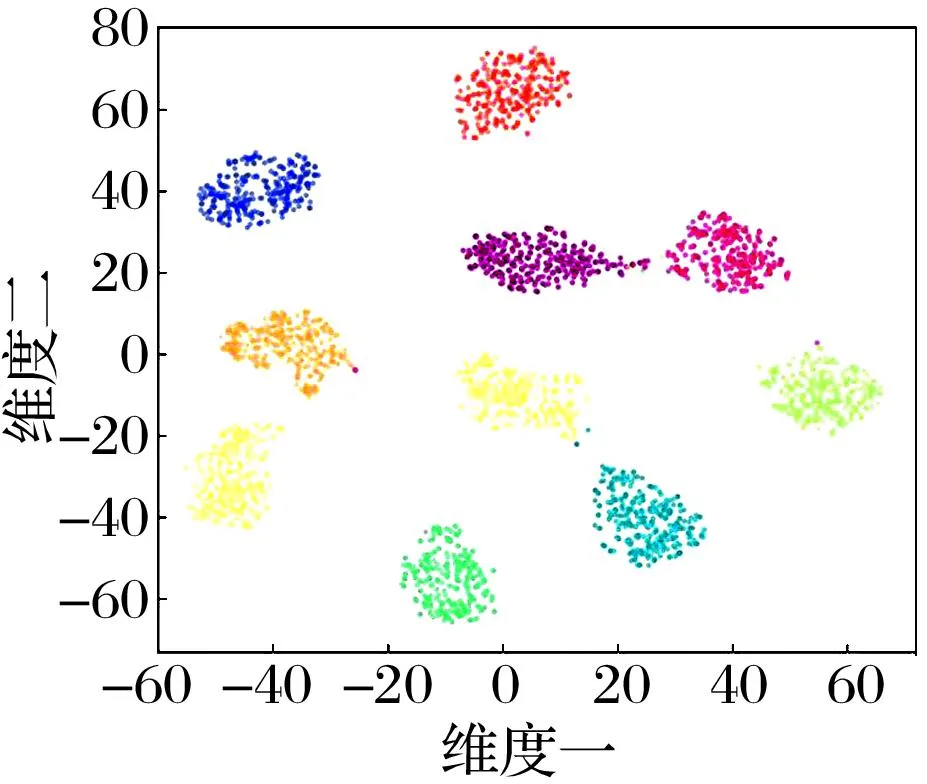
(a) SSDAE_NOLcg

3.3 对比分析

选取4种相关的方法(LGSSAE[9],FDSAE[11],DisAE[10]和BNAE[4])进行对比分析以研究SSDAE方法的故障诊断性能。分别在4组样本集上进行试验,每种方法在每组样本集的测试结果选择10次结果的均值以避免试验结果存在的随机性。

由表3的试验结果可知:BNAE的表现较差,最高平均准确率仅85.07%;LGSSAE和FDSAE表现相差不大,均在样本集A上取得了最高平均准确率,分别为88.45%和92.87%,尽管FDSAE的最高平均准确率高于LGSSAE,但LGSSAE的标准差更小,即其稳定性优于FDSAE方法;DisAE取得了较好的诊断效果,最高平均准确率达97.25%,而且标准差数值较小,体现了良好的稳定性;本文SSDAE方法的标准差与DisAE相差不大,同样表现出了较高的稳定性,而SSDAE方法的最低平均准确率也高达98.80%,表现出良好的准确性。

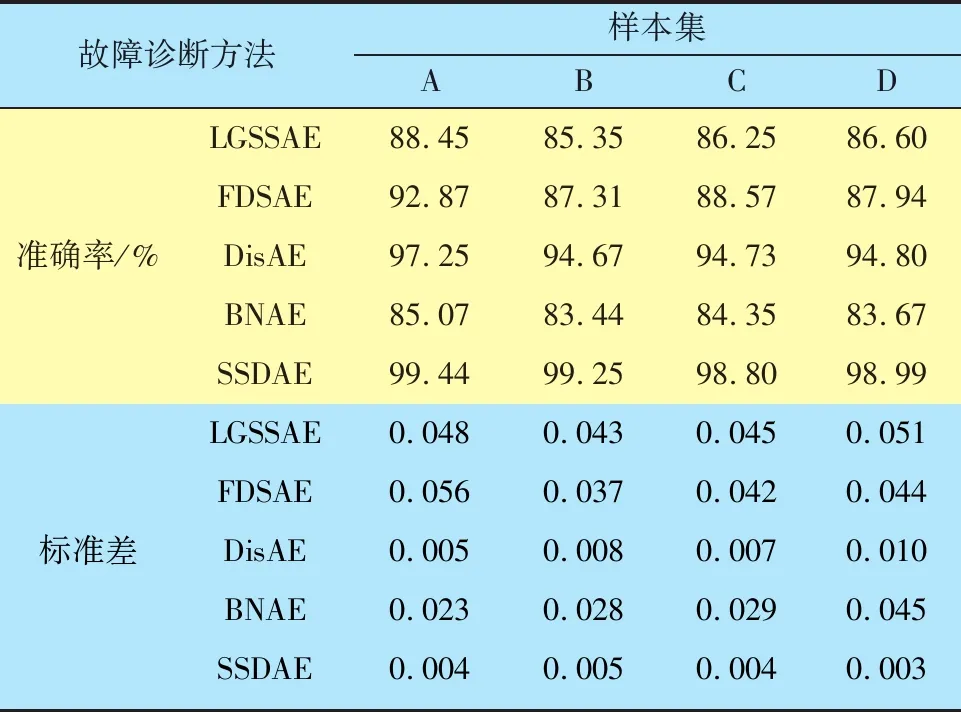
表3 不同方法在测试集上的平均准确率

为更直观地分析这几种方法的诊断效果,选取其在样本集D上连续的10次试验结果进行分析,如图7所示:SSDAE和DisAE具有良好的稳定性,各次试验的准确率相差不大;与其他4种方法相比,SSDAE方法展现出了最优的诊断准确率,体现了该方法的准确性和稳定性。

3.4 可视化分析

为进一步分析SSDAE方法的性能,将其在样本集D上的第10次试验结果可视化,混淆矩阵如图8所示:所有类型的故障均在训练集上实现了100%的准确率,说明该方法对数据有较强的学习能力;测试集中,虽然故障类型1,2,3,6,7有个别错分的数据,但其余故障类型则实现了100%的准确率,说明SSDAE能够对数据特征进行良好的识别,实现可靠的故障诊断。

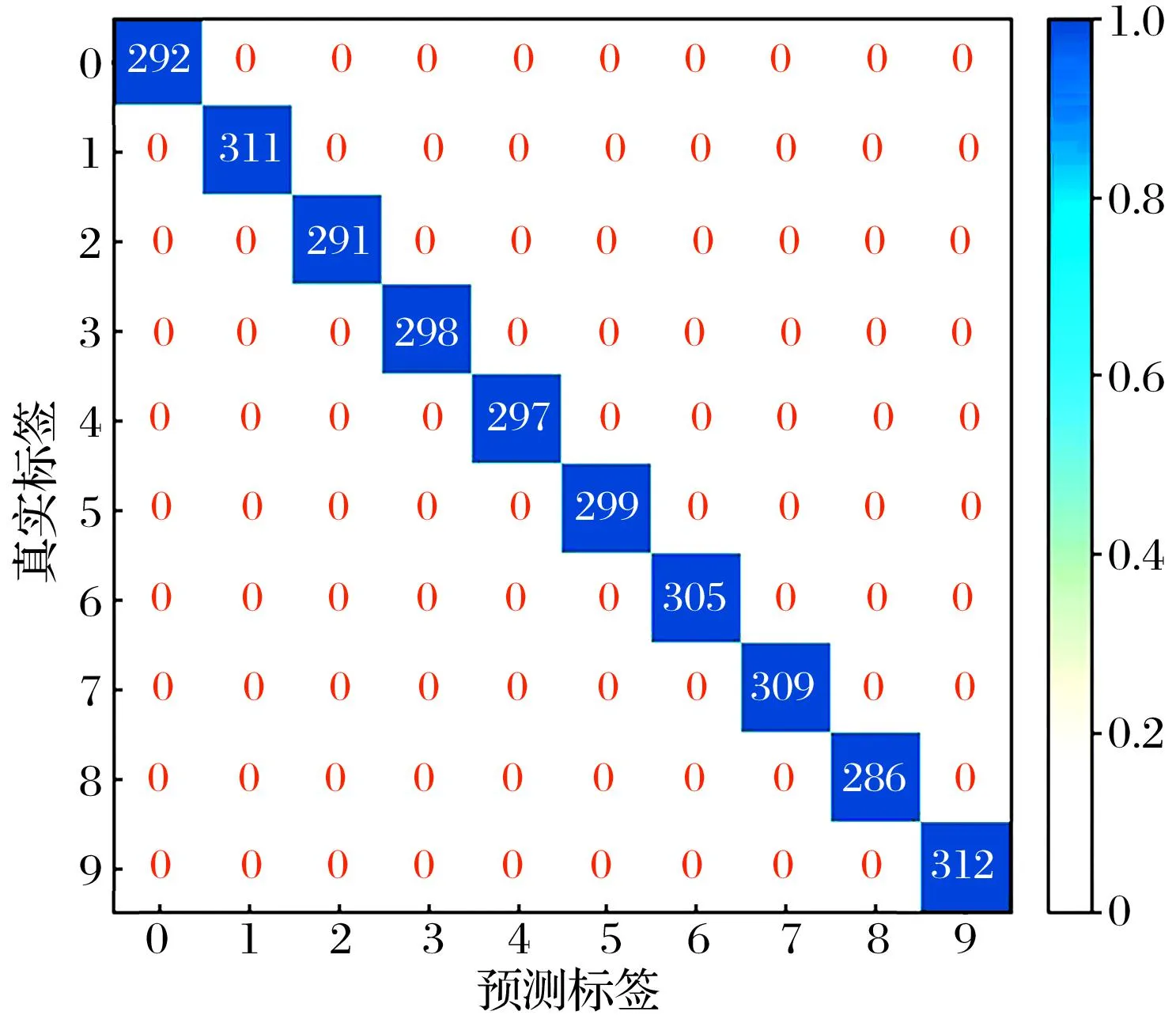
(a) 训练集

4 结论

本文提出了一种可用于复杂工况下旋转机械部件故障诊断的堆叠稀疏判别自编码智能故障诊断算法,通过CWRU数据集的试验验证得到如下结论:

1)半监督机制能够改良传统无监督网络,增强网络分类性能。

2)所提出的样本结构特征约束机制能够从样本几何特征角度和样本数据结构角度约束特征重构的方向,增强自编码网络的特征提取能力。

3)SSDAE方法在多组样本集的多次试验中均取得了良好的故障诊断准确率,具有较强的可靠性和稳定性。