磁悬浮轴承系统跌落转子-保护轴承的动态响应分析

马子魁,赵东旭,倪艳光

(1.舍弗勒贸易(上海)有限公司(安亭轴承研发中心),上海 201804;2.河南科技大学 机电工程学院,河南 洛阳 471003)

主动磁悬浮轴承系统由于具有高速旋转、无机械摩擦、能耗低、噪声小、寿命长、无需润滑以及无污染等优点被广泛应用于现代工业以及航天领域[1]。磁悬浮轴承系统由转子、传感器、控制器和执行器4部分组成,结构复杂,有时会因掉电或过载等因素导致转子失稳跌落,存在一定的安全隐患。因此保护轴承是磁悬浮轴承系统必不可少的一部分,主要起支承、应急、保护的作用,极大提高了磁悬浮轴承系统的安全裕度[2]。

当磁悬浮轴承失效时,转子在重力作用下以极高的转速跌落至保护轴承内圈上,转子是整个系统的动力来源,所以转子的运动轨迹、转子与保护轴承内圈的碰撞力对系统的安全极其重要:文献[3]基于单盘转子系统建立了转子跌落在保护轴承上的运动方程,分析了跌落转子转动角速度、转子与保护轴承内圈碰磨接触点的法向力随时间的变化过程及保护轴承瞬态振动位移频谱,发现转子减速通过一阶临界转速时引起的强烈非稳态受迫弯曲振动加上轴颈与保护轴承之间的高频振动是导致系统发生破坏的可能原因;文献[4]用有限元法建立了固定间隙保护轴承-电磁轴承-柔性转子系统在主动电磁轴承失效前后的动力学方程,分析了转子的初始跌落位置、转速、转子不平衡量以及保护轴承的刚度、阻尼对转子在跌落过程中瞬态动力特性的影响,发现转子不平衡量的增加将会导致保护轴承与转子的碰撞力、转子涡动增大,而具有外阻尼的柔性保护轴承能够有效减小保护轴承与转子的碰撞力、转子涡动;文献[5]对高速转子跌落在保护轴承上的碰撞力进行了理论分析和试验研究,提出了通过转子跌落后支承环的振动加速度信号反推碰撞力的测量方法,验证了标定碰撞力模型的有效性;文献[6]利用多体动力学软件对转子跌落到保护轴承上的动态过程进行了仿真,结果表明随着转子不平衡等级和跌落转速的增加,保护轴承与转子的轴向碰撞力几乎不变,但径向碰撞力随之增加;文献[7]提出了通过安装冲击力传感器测量转子与保护内圈碰撞力的方法,并验证了该测试方法的准确性。

轴承的急加速、高转速并且伴随冲击的作用都会对滚动体或保持架造成剧烈的损伤:文献[8]列举了多个由于保护轴承失效而导致整个跌落转子-轴承系统破坏的案例,所以保护轴承的设计和内部动态响应是不可忽视的因素;文献[9]通过有限元法对工作过程中保护轴承保持架进行受力和振动分析,发现仅考虑离心力的作用,保持架的最大应力分布在保持架侧梁中心处,并且该应力值已经接近材料的屈服强度,建议采用无保持架的保护轴承; 文献[10]分别建立了无保持架和有保持架的轴承简化模型和基于多体动力学的轴承模型,在同一工况下对2种轴承和2种模型的轴承-转子动态响应进行了对比分析,指出设计保护轴承结构时需要建立详细的轴承多体动力学模型进行计算; 文献[11]分析了保护轴承中钢球直径偏差对轴承-转子系统的影响,结果表明直径出现偏差钢球的尺寸和位置会改变轴承内部的载荷分布和最大接触应力;文献[12]考虑了保护轴承-转子的碰撞和摩擦引起的热效应,分析了滚道波纹度的频率和幅值对轴承内部接触力和摩擦功耗的影响,发现随着表面波纹度频率和幅值的增加,保护轴承的摩擦功耗、球之间的碰撞力、转子与保护轴承内圈的碰撞力均增加;文献[13]通过Adams建立了立式转子跌落模型,分析了转子初始转速、转子与保护轴承内圈的摩擦因数对转子与保护轴承内圈最大碰撞力的影响,并通过转子跌落试验发现导致应急失效的主要原因是转子与保护轴承内圈内径面的滑动摩擦生热。

目前针对跌落转子-轴承系统中转子轨迹、转子与保护轴承内圈碰撞力的研究已相对完善和成熟,但建立轴承完整动力学模型,分析转子跌落过程中保护轴承动态响应的研究相对较少。本文通过有限元软件Abaqus和舍弗勒轴承动力学软件Caba3D建立柔性跌落转子-保护轴承的动力学模型,研究转子跌落过程转子质心轨迹、转子与保护轴承内圈的碰撞力、保护轴承内相邻球的碰撞力、球与保护轴承套圈之间的滑动速度随时间的变化过程,为磁悬浮轴承系统中转子-保护轴承系统的动力学仿真提供基础理论,为系统的动力学现象分析提供参考。

1 跌落转子-保护轴承系统模型

1.1 磁悬浮轴承系统结构

磁悬浮轴承系统原理[8]如图1所示,该系统正常工作时磁悬浮轴承利用可控电磁力将转子悬浮在定子中间;当转子位置发生位移时,位移传感器会通过控制器、功率放大器和电磁铁调整轴承的电磁力,进而维持转子的稳定悬浮。所以与普通轴承-转子系统相比,磁悬浮轴承系统具有无接触、无润滑、无磨损等优点。当磁悬浮轴承系统发生故障时,转子以极高的转速跌落在保护轴承上,对保护轴承的抗冲击性、极限转速、润滑性能等提出极大的挑战。

1.2 跌落转子-保护轴承系统模型

由德国舍弗勒技术公司开发的Caba3D是目前最强大的滚动轴承动态仿真软件之一,与传统的商业软件相比,Caba3D具有多种固体摩擦模型和弹性流体润滑模型。Caba3D模型计算中还可根据实际工况设置每个零件的移动自由度和旋转自由度,在接触计算中考虑了材料阻尼、油阻尼及接触物体之间的弹性力、滚动摩擦、滑动摩擦等因素。并且Caba3D中的关键计算数值已经过多个试验验证[14]。

本文以某磁悬浮轴承系统为例,进行跌落转子-保护轴承系统的动态响应分析。磁悬浮轴承失效后,转子以42 000 r/min的转速自由落体,与保护轴承接触,可将磁悬浮轴承系统简化为跌落转子-保护轴承系统,如图2所示,深沟球轴承主要承受径向力,角接触球轴承主要承受轴向力。由于保护轴承从静止迅速增加到极高的转速,一方面加速过程中球与保持架之间会产生巨大的碰撞力,另一方面保持架在高速离心力作用下会产生巨大的应力,这将对保持架性能提出极高的要求,所以保护轴承选用无保持架的满装球轴承; 为减小高速离心力的作用,球均采用密度较低的陶瓷材料;为降低跌落转子-保护轴承系统中碰撞面的滑动摩擦生热,该系统的接触表面均进行表面涂层处理。转子、保护轴承的结构、材料及部分工况参数见表1—表3。

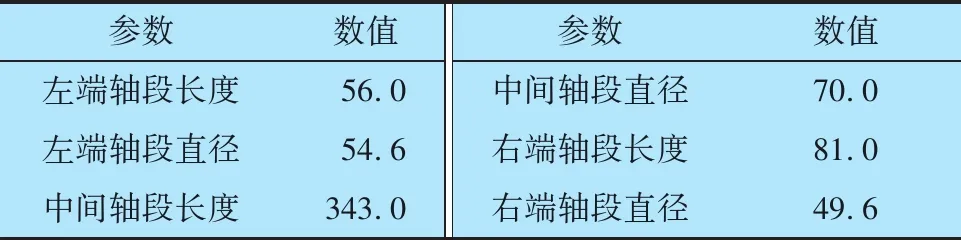
表1 转子的结构参数

表3 保护轴承和转子的材料及工况参数

图2 跌落转子-保护轴承系统简化模型

1.3 跌落转子-保护轴承动力学模型

1.3.1 柔性转子动力学模型

当磁悬浮轴承系统失效后,转子失去了动力来源和磁悬浮轴承的支承,进行自由落体运动。转子最高转速为42 000 r/min,小于它的一阶临界转速,但转子一直处于非稳态状态,为使计算更接近实际情况,将转子视为柔性体进行计算。转子弯曲振动的运动微分方程为

(1)

式中:qs为转子系统的位移矢量;Ms,Cs,Gs,Ks分别为转子的质量矩阵、阻尼矩阵、陀螺矩阵及刚度矩阵;Fs,g为转子受到的重力矢量;Fin-s,c为保护轴承内圈对转子作用力矢量。

1.3.2 保护轴承动力学模型

保护轴承的坐标系如图3所示。在重力、球和转子的作用下,保护轴承内圈的动力学微分方程为

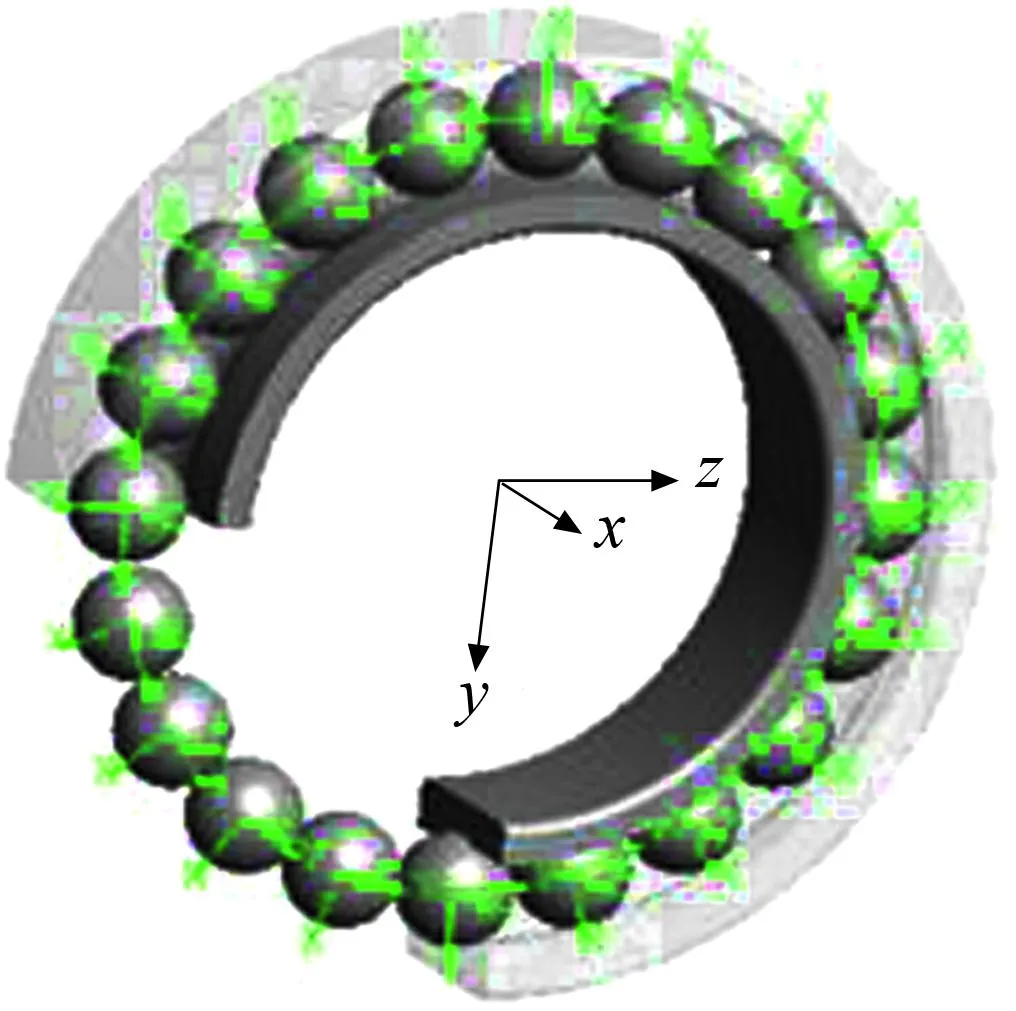
图3 保护轴承的坐标系

(2)

保护轴承内球的受力情况如图4所示。

(a) x-z平面 (b) x-y平面 (c) y-z平面

由图4可得球的动力学微分方程为

(3)

1.3.3 柔性转子模型的建立

有限元模型自由度较多,动力学仿真需要较长的时间,大量增加多体动力学仿真成本,通常对有限元模型进行简化。柔性转子的变形较小,转速较大,浮动坐标系方法是最合适的有限元模型简化方法[15],可将弹性物体的运动视为浮动坐标系的大范围运动与小弹性变形的叠加。

在有限元商业软件Abaqus中使用浮动坐标系将简化有限元模型导入Caba3D中,Caba3D的预处理模块会对简化模型与完整模型的自然频率、固有模态进行对比验证,并检查简化模型的阻尼比。柔性转子模型如图5所示。

图5 Abaqus柔性转子模型

1.3.4 接触模型

切片法是Caba3D中计算刚体接触的基本方法。在计算过程中先将模型切分,如图6所示。在每个计算步中都会计算接触对的切片距离来判断2个切片是否发生接触。

图6 切片接触模型[16]

对于刚柔耦合接触则采用点-面接触模型(图7),在计算过程中通过解析法得到柔性体节点与刚性体之间的距离并判断2个物体是否发生接触。

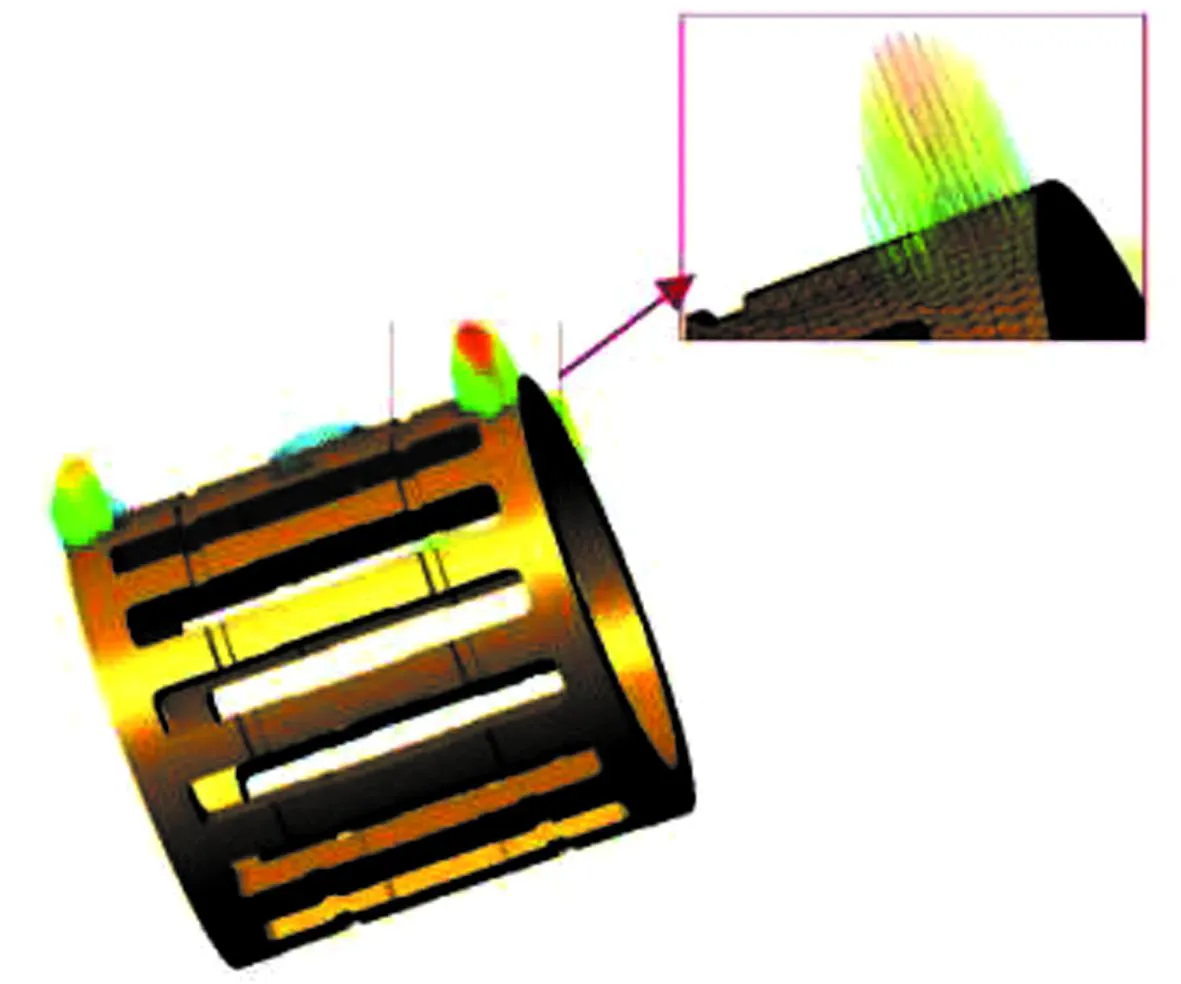
图7 点-面接触模型中应力分布[16]

2 跌落转子-保护轴承仿真分析

转子开始高速跌落到转速为0的仿真时间过长,由计算结果可知转子跌落过程中跌落转子-保护轴承系统的不稳定因素主要集中在保护轴承内圈加速阶段,当保护轴承内圈的转速与转子相同后,跌落转子-保护轴承系统很快达到相对稳定的运动状态,因此以下仿真结果从转子跌落开始,直到保护轴承内圈转速与转子相同后一段时间内结束。

2.1 转子和保护轴承内圈的转速

转子和保护轴承内圈转速随时间的变化如图8所示。在宏观上,由于转子惯性远大于保护轴承内圈,所以在转子与内圈接触时,转子以极低的转速下降,而内圈转速以非常高的速度上升,这是因为转子质心偏向深沟球轴承一侧,转子与深沟球轴承内圈的碰撞力更大,在2.2 s时深沟球轴承内圈的转速首先与转子几乎一样;两角接触球轴承为面对面配置,当与跌落转子接触时,两内圈侧面之间会产生接触力(图9),使其内圈转速始终保持一致并在3.3 s时与转子转速一致并与转子一起减速。在微观上,转子在保护轴承内圈上反复弹跳,与保护轴承之间并非处于持续接触状态,所以内圈转速波动上升;转子转速也并不是随时间线性降低,当深沟球轴承、角接触球轴承内圈转速与转子达到几乎一致时,转子与内圈之间的摩擦力降低,转子转速降低速率减小;在转子和保护内圈转速相对稳定下降的阶段,内圈之间转速相差较小,而转子与内圈的转速差约为300 r/min。

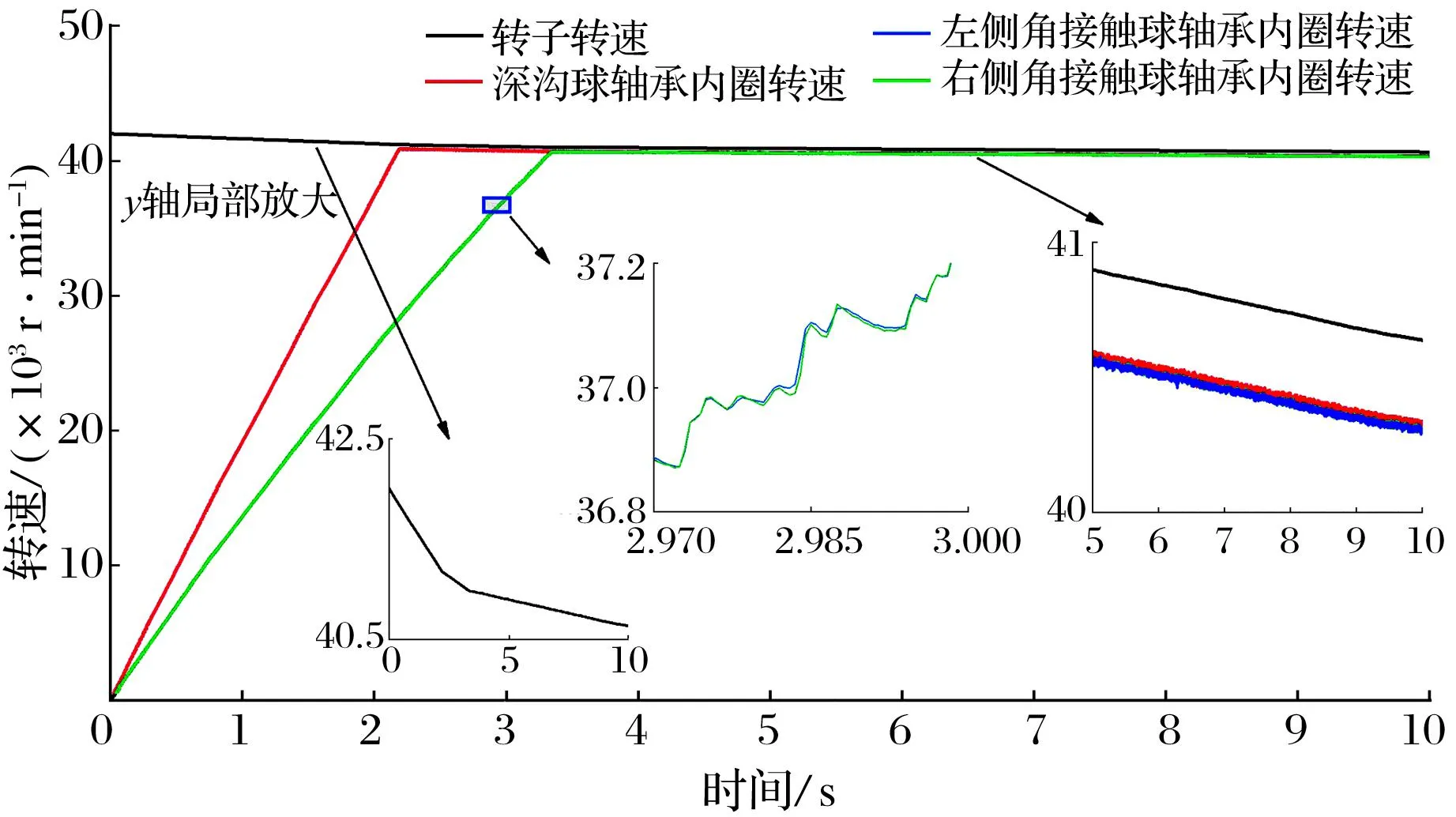
图8 转子和保护轴承内圈转速

图9 两角接触球轴承内圈轴向接触力

2.2 转子质心轨迹、转子与保护轴承内圈的碰撞力

转子在y-z平面内的质心轨迹如图10所示,转子质心在y,z方向上随时间的变化如图11所示,保护轴承内圈与转子之间的碰撞力随时间的变化过程如图12所示。根据图10可知,转子质心在5～10 s内相对稳定,为更清晰地表达转子质心轨迹、转子与内圈之间碰撞力的关系,在本节中只对0～5 s进行分析。

(a) 0～5 s转子质心轨迹

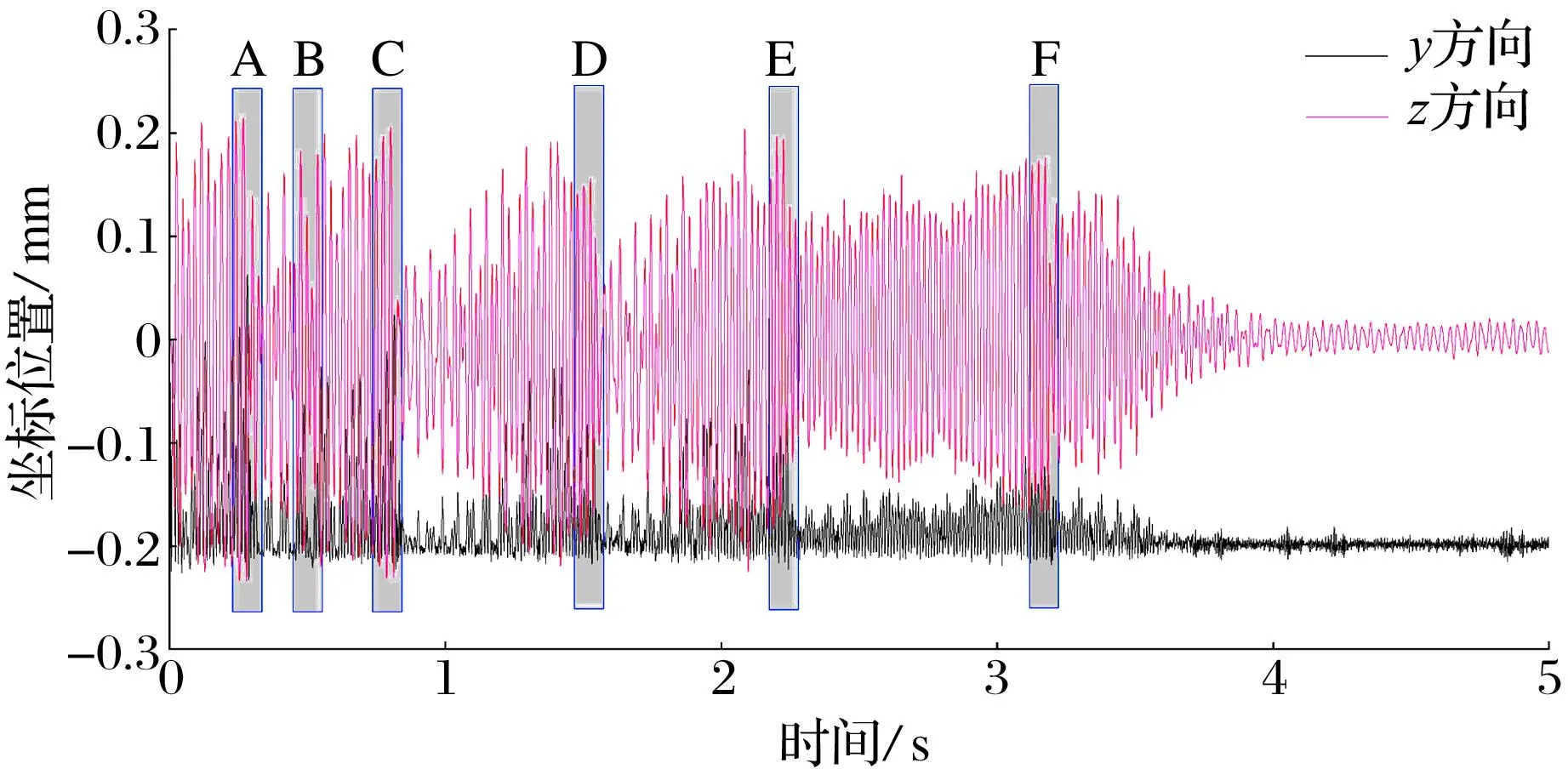
图11 y和z方向转子质心的运动过程

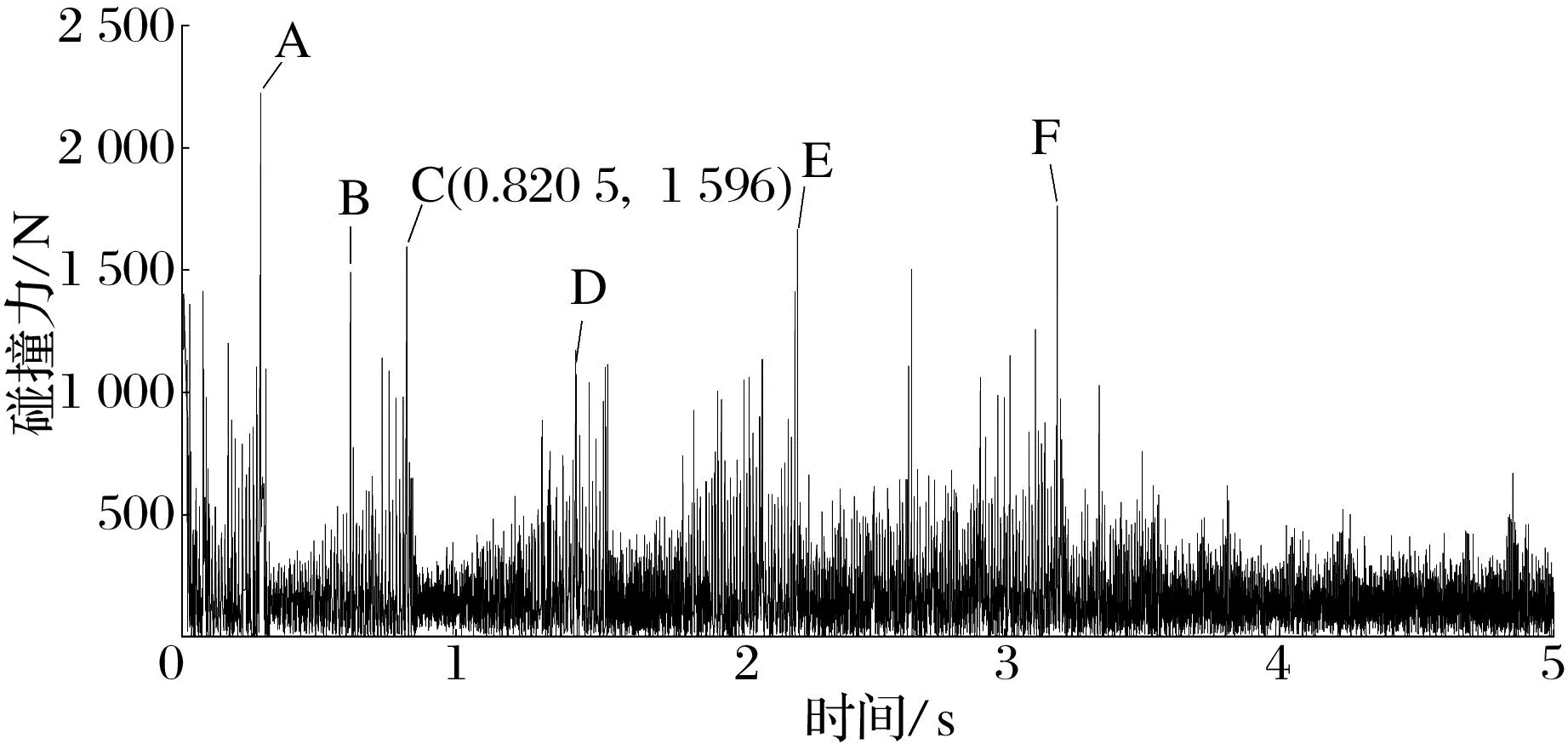
(a) 深沟球轴承与转子的碰撞力

转子的质心轨迹、转子与保护内圈的碰撞力主要受转子与保护轴承内圈的滑动速度、转子的跌落高度、转子的跌落位置等多因素影响,通过对比图10—图12可得到转子质心轨迹以及转子与保护轴承内圈碰撞力的变化规律。

由图10和图11可知:转子首先从0点做自由落体运动,与保护轴承内圈发生碰撞和摩擦,经一次大幅度反弹上抛、自由坠落后,转子开始在保护轴承内圈上进行规律的摆动和跳动;随摆动次数的增加,转子摆幅逐渐增大,当增大到临界值时,与保护轴承内圈脱离;转子经数次上述自由落体、摆动以及跳动后,保护轴承内圈转速与转子转速逐渐接近,转子的摆幅也逐渐变小,最终转子在保护轴承内圈上小幅滑动和小幅跳动。

由图12可知,转子质心偏向深沟球轴承一侧,所以转子与深沟球轴承内圈的碰撞力比转子与角接触球轴承内圈的大得多,两角接触球轴承内圈与转子的碰撞力相差较小。由于转子与深沟球轴承的碰撞力变化最明显,后续分析时主要关注深沟球轴承与转子之间的动力学关系。对比图9、图11、图12a可知,导致转子与深沟球轴承内圈之间碰撞力剧增的主要原因是转子脱离深沟球轴承内圈发生自由坠落引起的碰撞力,规律较明显的时间区域A,B,C,D,E,F已在图11和图12a中标出。以0.65～0.85 s的运动轨迹图(图13)为例,C区域前转子在x和y方向上的波动幅值随时间增加,转子也会与轴承内圈脱离,发生小幅跌落而引起碰撞力增大;在C区域时,转子从较高的位置跌落至深沟球轴承内圈上,转子轨迹在x和y方向上的波动幅值显著降低,而该时刻的碰撞力突然增大。

(a) C区域转子质心的运动轨迹

2.3 保护轴承内相邻球之间的碰撞力

相邻球之间是否发生碰撞以及碰撞力大小受球公转速度、球质量、相邻球之间相互作用时间等因素的影响,随机性较大。分别确定各套保护轴承内产生最大碰撞力的2个球,并提取这2个球之间的碰撞力和接触应力随时间的变化趋势,结果如图14所示,相邻球之间的最大碰撞力为175 N,最大接触应力为5 684 MPa。陶瓷属于脆性材料,陶瓷球失效形式为脆性破坏,直径8.5 mm的氮化硅陶瓷毛坯压碎载荷为17.9 kN[17],其对应的接触应力为27.7 GPa,所以该工况下陶瓷球还有相当大的承受载荷余量。

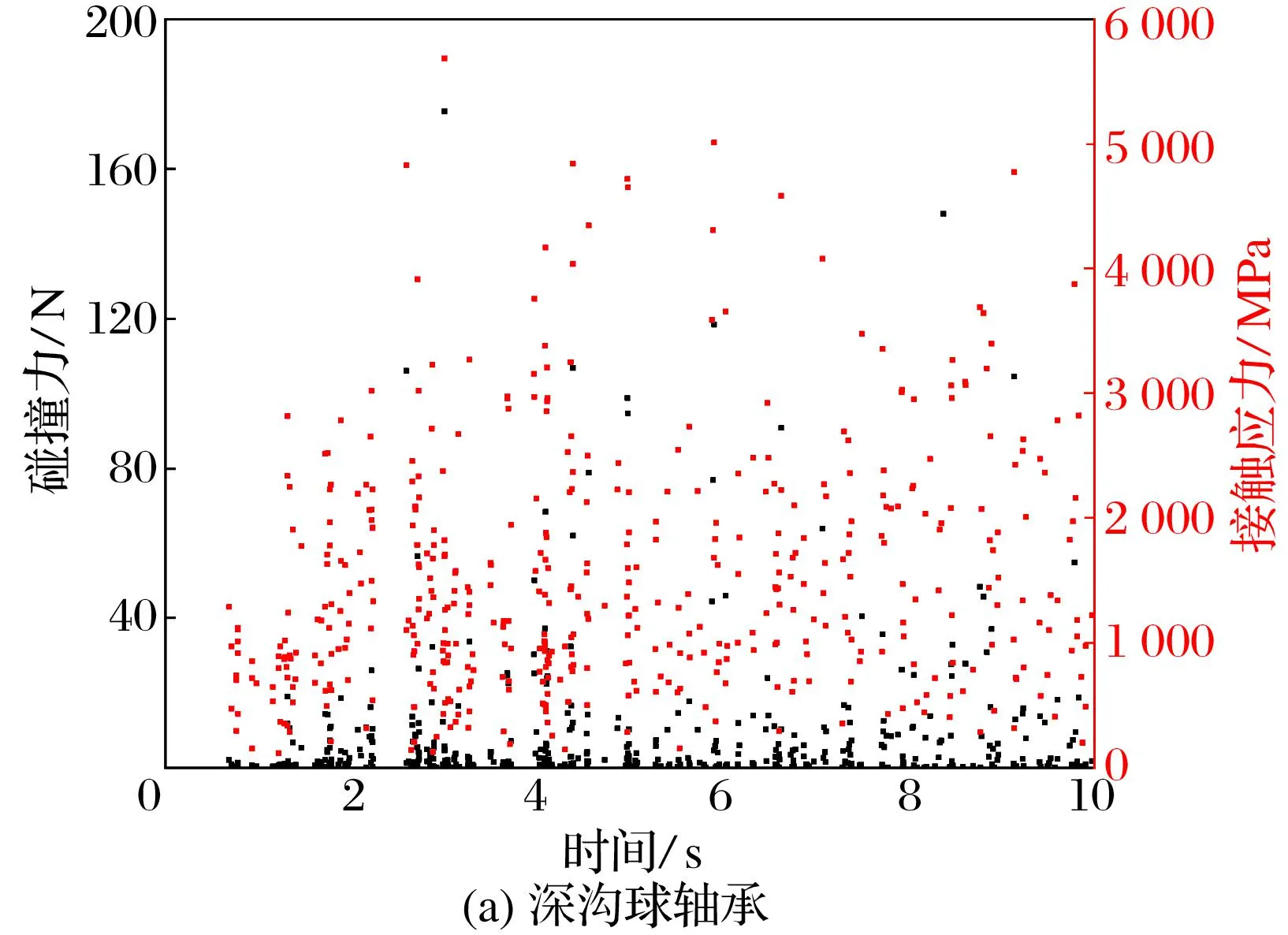
图14 轴承内相邻陶瓷球之间的碰撞力和接触应力

2.4 球与保护轴承内圈沟道的滑动速度

球轴承的滑动速度主要分为陀螺滑动、自旋滑动、差动滑动和高速打滑这4种形式。高速球轴承的滑动会引起摩擦发热和磨损,导致轴承损伤而过早失效,所以球轴承的滑动速度一直广受重视。

保护轴承内圈与其中一个球之间的滑动速度随时间的变化过程如图15所示。由图15和图8可知:随着时间增加,在内圈加速阶段,球与内圈的滑动速度逐渐增加;当内圈转速与转子几乎相同时,内圈与球的滑动速度波动状态也趋于稳定。这是因为:1)加速阶段,球的公转速度在内圈拖动力的作用下增加,所以球的公转速度始终滞后于内圈转速;2)随着转速增加,内圈对球的拖动作用逐渐降低,导致球与内圈的滑动速度逐渐增加;3)相对稳定阶段,内圈转速逐渐下降,但下降速度非常低,轴承处于相对稳定的状态,内圈与球的滑动速度趋于稳定的波动状态。

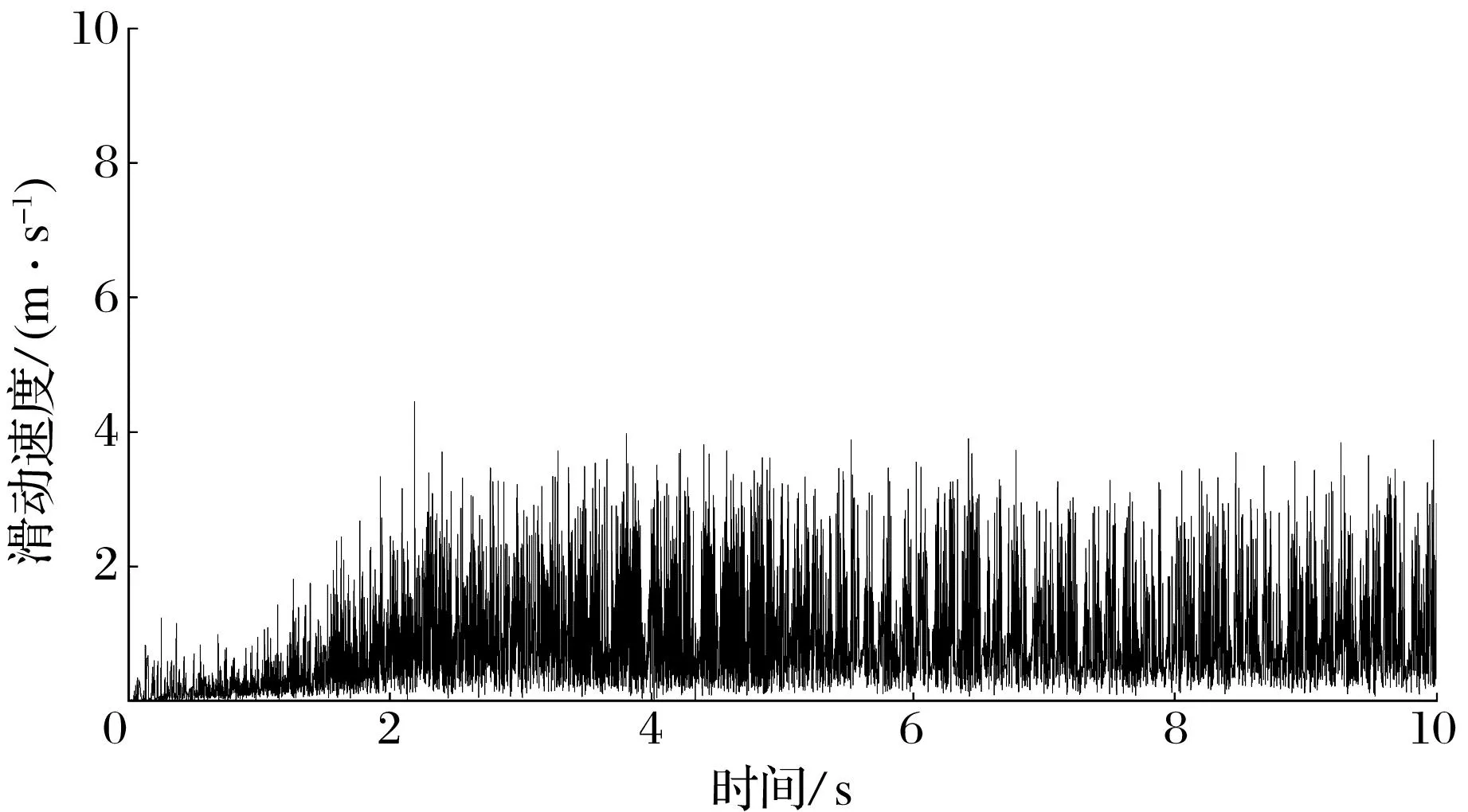
(a) 深沟球轴承

通过图15横向对比角接触球轴承和深沟球轴承中球与内圈的滑动速度可知,在保护轴承内圈加速阶段,随着时间的推进,角接触球轴承中球与内圈的滑动速度波动值大于深沟球轴承中球与内圈的。这是因为:1)角接触球轴承容易发生陀螺滑动,陀螺滑动主要受球的转动惯量,球公转速度、球自转速度的影响,随着球公转速度和自转速度的增加,角接触球轴承中陀螺滑动速度进一步增加;2)角接触球轴承比深沟球轴承更容易发生自旋滑动。

3 结论

通过有限元软件Abaqus和轴承动力学软件Caba3D建立了柔性转子-保护轴承的动力学模型,对转子的质心轨迹、转子与保护轴承内圈的碰撞力、保护轴承内部的动态响应进行了分析,得到以下结论:

1)转子跌落后,宏观上转子转速以较低的速度下降,而保护轴承内圈转速以较高的速度上升;微观上保护轴承内圈转速波动加速,当保护轴承内圈转速与转子相同时,转子减速度降低。

2)经历几次反复弹跳-自由落体后,转子在保护轴承内圈上反复摆动,随着摆动次数增多,转子的摆幅增大,到达临界值后转子与保护轴承内圈脱离,转子自由落体与保护轴承内圈再次接触并产生较大的碰撞力;当保护轴承内圈的转速与转子相同后,转子会在保护轴承内圈底部稳定小幅摆动和小幅跳动。

3)在42 000 r/min的转子跌落工况下,在保护轴承加速阶段和高速阶段,保护轴承内部陶瓷球不会失效,并且还有余量承受更大的载荷。

4)在保护轴承加速阶段,球与内圈的最大滑动速度逐渐增加,当轴承与转子的转速几乎相同时,球与内圈的最大滑动速度和滑动速度波动状态也趋于稳定。

本文首次计算并分析了磁悬浮转子-轴承系统中保护轴承内部的动力学特性,通过分析球与球之间的碰撞力和接触应力揭示了在此工况下陶瓷球之间并不会因为内圈极高的加速度而产生脆性破坏,并且还有较大的余量;通过分析转子与保护轴承内圈之间以及球与内圈之间的滑动速度随时间变化的趋势,该系统的温升主要由滑动摩擦引起,也反映了温度随时间的变化趋势,为实际应用中应对系统温升过高提供参考;通过系统整体分析可知,该结构和材料参数下的转子运行状态相对稳定,保护轴承内部不会发生严重的损坏,为该系统的结构设计提供了参考。