嵌入小实验：数学作业设计新探

崔宏宇

摘 要：小学数学实验是指在数学思想和数学教学理论的指导下，学生借助实物和工具，通过对实验素材进行“数学化”的操作来验证数学结论、建构数学概念、探索数学规律、解决数学问题的一种数学学习方式。数学作业中也应适当嵌入小实验，如“阶梯式”小实验、“反复式”小实验、“探索式”小实验等，引领学生更真切地触摸数学本质。

关键词：小学数学；作业设计；小实验

“数学实验”最早出现在数学家波利亚的《数学与猜想》一书中：“完整的数学应包含两个侧面，一个是欧几里得式的严谨科学，另一个是实验性的归纳科学。”  ［1］ 伴随着基础教育课程改革的逐步深入，实验教学被纳入国家课程方案和课程标准规定的重要教學内容，成为培养创新人才的重要途径。根据数学学科特点和小学生数学学习特点，小学数学实验被界定为：在数学思想和数学教学理论的指导下，学生借助实物和工具，通过对实验素材进行“数学化”的操作来验证数学结论、建构数学概念、探索数学规律、解决数学问题的一种数学学习方式。

［2］ 作业是学习的重要板块，数学作业中也应适当嵌入小实验，引领学生更真切地触摸数学本质。笔者在低年级的数学作业设计中进行了尝试，下面分享几点做法。

一、嵌入“阶梯式”小实验

教材中的一些思考题，具有很强的操作性。围绕这类问题设计作业时，可依此“蓝本”，将一个问题转译成更符合学生年龄特征的“阶梯式”小实验，从“一个”拓展到“一类”，帮助学生循序渐进地发现规律、应用规律。

例如，苏教版小学数学一年级上册《认识10以内的数》的思考题（见下页图1），旨在让学生初步感受绳子的段数（根数）与结的个数间的关系。

为帮助学生在动手做的过程中自主发现规律，我们可以在作业中“放大”操作的次数，将其转化为“阶梯式”小实验：

实验工具：绳子若干。

实验内容：

实验一：将2根绳子连在一起，要打（  ）个结。

实验二：将3根绳子连在一起，要打（  ）个结。

实验三：将4根绳子连在一起，先想一想，猜一猜，要打（  ）个结；再动手将4根绳子连在一起验证一下，实际打了（  ）个结。

实验四：将5根绳子连在一起，要打（  ）个结；将6根绳子连在一起，要打（  ）个结；将7根绳子连在一起，要打（  ）个结；将8根绳子连在一起，要打（  ）个结……

和爸爸妈妈说一说你的发现。

学生反复操作后，发现了规律：结的个数总是比绳子的段数（根数）少1。这样的“阶梯式”数学小实验，加深了学生的操作体验，为思维的爬坡搭建了阶梯。

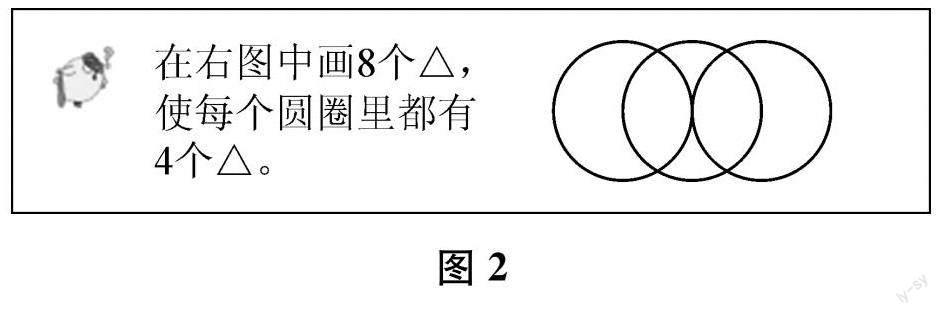
又如，苏教版小学数学二年级上册《表内除法（一）》的思考题（见图2），旨在帮助学生初步体会集合的思想和方法，感受解决问题的策略，发展思维。

在设计作业时，我们从简单问题入手，“拉长”操作的步骤，转化为“阶梯式”小实验：

实验工具：三角形学具。

实验内容：

实验一：在图3中摆4个三角形，你能让每个圆圈里三角形的个数相同吗？

实验二：在图4中摆4个三角形，你能让每个圆圈里三角形的个数相同吗？

实验三：在图5中摆4个三角形，你能让每个圆圈里三角形的个数相同吗？

实验四：在图6中摆8个三角形，你能让每个圆圈里三角形的个数相同吗？

实验五：在图7中摆12个三角形，你能让每个圆圈里三角形的个数相同吗？

学生通过实验，不难发现“每个圈里三角形的个数之和-重叠部分=三角形的总个数”。这样的设计，为学生的知识建构铺设了思维的通道和方法的台阶。

建构主义学习理论认为，学生的学习是不断体验、不断积累的过程。嵌入“阶梯式”小实验的作业，旨在帮助学生探寻解决某类问题的一般策略。很多“高深”的数学思想方法也由此埋下了种子，让学生体验、感悟，然后逐步明晰、精确，进一步提升能力和素养。

二、嵌入“反复式”小实验

小学低年级学生对于数学思想的感悟，往往需要经历反复的过程。教师可在作业中设计让学生反复操作的小实验，进而从实验现象与实验结论之间关系的反思中，领会其中蕴含的数学思想。

例如，苏教版小学数学一年级上册《分与合》中的一道练习题（见图8），其情境是：同一只蚂蚁只能住在一间房里，不能同时住在不同编号的房里；编排意图是：让学生在开放的情境中，灵活运用数的分与合知识解决问题。

分析素材，发现这是一个非常典型的“一题多解”，还蕴藏着有关排列组合的数学思想方法。所以，就利用学生的数字卡片，在作业中设计了“反复式”小实验：

实验工具：数字卡片1、2、3、4、4、5、5、6、7、8、9。

实验内容：小蚂蚁们要搬到它们的新家蘑菇屋啦！小朋友们，你们能帮它们按要求（图8中两只蚂蚁住在一起）分一分吗？用你的数字卡片来摆一摆吧！当然，别忘了记录实验结果。比一比，看看谁的分法多。

这一“反复式”小实验，看似让学生重复完成同一任务，实则引导他们在操作的过程中不断拓展思维的边界，感悟直观背后的抽象。

又如，苏教版小学数学二年级下册《认识万以内的数》中的两道思考题（见图9、   图10 ），旨在加深学生对万以内数的认识，让他们初步感受有序思考在解决问题过程中的作用，体验列举这一解决问题的策略。

结合学生的年龄特点，我们在作业中设计了如下“反复式”小实验：

实验工具：数字卡片1、2、3、5、0、0。

实验内容：

实验一：用1、2、3、5四张数字卡片可以摆出多少个不同的四位数？先摆一摆，再从小到大排一排。

实验二：用1、2、3、0四张数字卡片可以摆出多少个不同的四位数？先摆一摆，再从小到大排一排。

实验三：用1、2、0、0四张数字卡片可以摆出多少个不同的四位数？先摆一摆，再从小到大排一排。

学生在从一般到特殊的“重复”中，不仅建立了有序思考的意识，发展了数学思考，还对其中蕴含的数学思想方法有了更深的体悟。

郑毓信教授指出：“数学教育的一个主要目的就是帮助学生学会思维，并能逐步学会想得更清晰、更全面、更深刻、更合理。”  ［3］ 嵌入“反复式”小实验的作业，在深化学生对相关知识理解的同时，拓宽了他们解决问题的思路，同样具有重要的价值。

三、嵌入“探索式”小实验

富有想象力和探索精神也是小学低年级学生表现出来的特征。因此，数学作业中还可以设计有一定难度的“探索式”小实验，让学生完整经历系列探究和验证的过程，发现规律，得出结论，巩固所学。

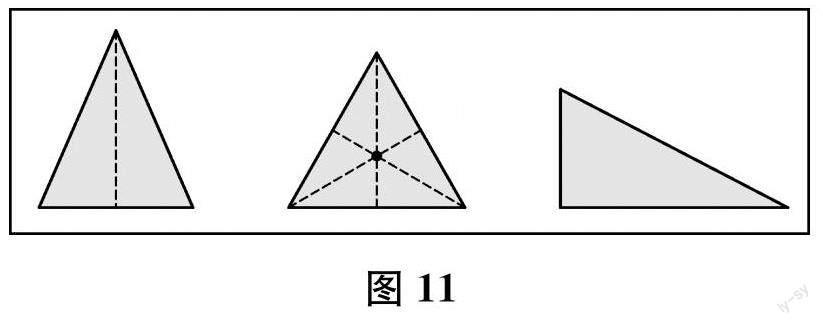
例如，基于苏教版小学数学一年级下册《认识图形（二）》的一系列练习题，笔者结合北师大版小学数学教材中《动手做》栏目的相关素材，布置了让学生将正方形纸、长方形纸、圆形纸和三角形纸折成一样的两部分并验证的“探索式”小实验。学生除了得到常规的方法外，还运用两次对折找中心点的方法，将图形折成一样的两部分。在课堂上进行展示时，还设计出了新的小实验：是不是经过这个点的所有折法都可以？这是一个非常典型的“探索式”小实验，还进一步推广到了长方形。另外，因为每个学生选择的三角形类型不同（见图11），也得到了不一样的结论。课堂上，我们也进一步进行了讨论：是不是所有的三角形都能分成一样的两部分？再让学生在课堂上做数学小实验，以期进一步发现问题、提出问题、分析问题、解决问题。

对图形的认识不能仅基于图形的定义，更重要的是从图形本身出发所获得的发现，依托小实验的探索过程让学生的数学思考有所依托，也为后续数学原理的探究奠定了基礎。

又如，苏教版小学数学二年级上册《平行四边形的初步认识》中的一道“想想做做”练习题设置了两个环节：第一环节是尝试将一

张四边形纸剪成两个三角形或者一个三角形和一个四边形，第二环节是探索在一张正方形纸上剪下一个三角形后剩下的部分是什么图形。这本身就是一组操作性和开放性较强的练习，有利于学生获得图形变换的经验，进一步发展学生的空间观念和实践能力。为了推广到更一般的情境中，我们对素材进行了二次加工，设计了如下“探索式”小实验：

实验工具：三角形、四边形、其他多边形纸片若干。

实验内容：

实验一：三角形剪下一个三角形后，剩下的图形是几边形？

实验二：四边形剪下一个三角形后，剩下的图形是几边形？

实验三：选择一种多边形剪下一个三角形后，剩下的图形是几边形？

这样的设计帮助学生对数学模型的外部表征进行操作体验，在直观感知的过程中建立起清晰的表象，对发现的规律进行有序概括，促进对抽象模型的建构。

苏霍姆林斯基曾说，在人的心灵深处，都有一种根深蒂固的需要，就是希望自己是一个发现者、研究者和探索者。在儿童的精神世界里，这种需要特别强烈。  ［4］ 嵌入“探索式”小实验的数学作业设计，能够帮助学生主动对所学数学知识进行探究，并在探索过程中促进思维能力的发展。

参考文献：

［1］ 丁银杰，殷容仪.常态化实施数学实验教学的路径和方法［J］.江苏教育，2019（83）：17.

［2］ 郭庆松.数学实验： 从研究方式到学习方式［J］.江苏教育，2017（17）：52.

［3］ 郑毓信.数学应让学生学会思维（上）——数学核心素养的理论性思考与实践性解读［J］.湖南教育（C版），2017（1）：23.

［4］ 沈胜林，张心，陈中文.基于新课标理念的中小学探究性学习特征与推进策略［J］.教学与管理，2023（25）：26.