饱和土不排水柱孔扩张计算的通用半解析解

2024-03-11刘贯飞雷胜友

水利水运工程学报 2024年1期

刘贯飞，雷胜友

(1.长安大学公路学院, 陕西西安 710064； 2.中国十九冶集团有限公司, 四川成都 610031)

在岩土工程中，孔的扩张理论是重要研究课题，涉及如隧道、井筒、沉桩等工程问题[1-2]，目前已有许多学者对此展开研究。早期的孔扩张理论大多基于以Mohr-Coulomb 屈服准则为代表的弹-理想塑性模型，如Vesić[3]、Carter 等[4]提出的孔扩张模型。由于推导方法和土体本构模型的限制，此时的孔扩张解仅可得到孔周的应力分布和基于不同屈服准则时的孔周弹塑性圈半径，不能反映土体应力历史和硬化行为的影响。为合理描述饱和土在圆孔扩张过程中的变形特点，Collins 等[5]采用原始剑桥模型（OCC）和修正剑桥模型（MCC），在假定孔周土有限应变的条件下，推导了各向同性硬化材料中的圆孔不排水扩张解，之后许多学者[6-7]以该解为验证依据。然而，由于该解答中对土的竖向应力进行了简化处理，不能真实反映饱和土中的柱孔扩张效应。Chen 等[8-9]基于MCC 模型使用拉格朗日分析法建立了K0固结饱和土中的不排水和排水柱孔扩张半解析解，该解答没有简化土体竖向应力。借鉴Chen 等[8-9]的研究方法，李镜培等[10]使用MCC 模型建立了饱和土中的不排水球孔扩张半解析解；李林等[11]、Sivasithamparam 等[12]考虑天然沉积饱和土的各向异性特点，采用改进后的MCC 模型推导了土中的不排水柱孔扩张解答；Zhai 等[13]使用改进的MCC 模型建立了结构性土中的不排水柱孔扩张解答。此外，Zhou 等[14]基于MCC 模型建立了同时适用于两种不同排水条件的饱和土中柱孔扩张统一相似解；武孝天等[15]基于CSUH 模型建立了适用于饱和黏土和砂土中的不排水柱孔扩张解。

以上基于MCC 模型或改进型MCC 模型建立的土中柱孔扩张解答，可以较好反映饱和土在径向受压变形过程中的应力变化和硬化特点，具有较大的理论意义。然而，由于临界状态土力学的复杂性，MCC 模型对正常固结和轻度超固结饱和黏土具有较好的适用性，但不适用于严重超固结土和颗粒材料[16-18]；另外，该类模型假设土的屈服函数形状及临界状态平均有效应力与硬化参数之间的比值均固定不变，这与实际并不相符。为此，本文使用统一状态参数模型（CASM）[18]和Rowe 剪胀方程[19]来描述土的弹塑性行为，结合大变形理论，通过引入辅助变量，使用拉格朗日分析法建立饱和土中的不排水柱孔扩张半解析解。

1 问题描述和本构模型介绍

1.1 柱孔扩张问题描述

无限均质饱和土中的不排水柱孔扩张如图1 所示。饱和黏土具有原始的竖向应力σ'v0、水平应力σ'h0=K0σ'v0、孔隙水压力u0及体积v0。柱孔初始孔径为a0，在均匀分布的内压力σa作用下发生扩张，随着σa的不断增大，孔周土随土质点与孔壁之间距离的增大逐渐发生屈服。扩孔结束后，孔周可分为已经屈服的临界状态区和弹塑性区，以及未屈服的弹性区，弹塑性区的半径为rp。假设此时的柱孔孔径为a，孔周某一土质点则从其初始位置rx0移动到了rx，应力状态从(σ'h0,σ'h0,σ'v0,u0)变为(σ'r,σ'θ,σ'z,u)。在上述柱孔扩张过程中，使用统一状态参数模型（CASM）来描述饱和土屈服后的弹塑性变形。

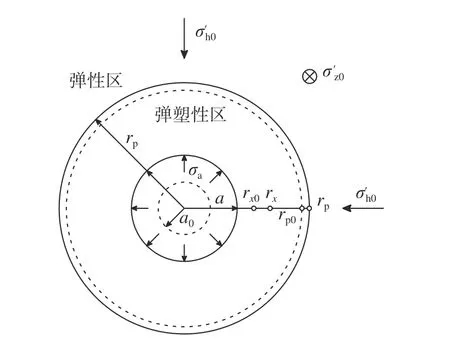
图1 不排水柱孔扩张示意Fig.1 Schematic diagram of undrained cylindrical cavity expansion

如图1 所示，可将饱和土中的柱孔扩张视为平面应变过程，在柱坐标系中建立土的应力平衡方程：

式中：σ'r、σ'θ分别为饱和土的径向、环向有效应力；u为土中孔隙水压力；r为土质点的径向位置。

1.2 统一状态参数模型（CASM）

基于土的状态参数概念和临界状态土力学理论，Yu[18]提出了能灵活描述黏性土和砂土受力变形行为的统一状态参数模型（CASM），近年来被许多学者用于分析饱和土中的旁压试验、静力触探和桩基沉降等工程问题[19-22]。CASM 模型的屈服面函数为：

式中：F(p',q,p'm)为土的屈服面函数；p'm为硬化参数；M为破坏应力比；如图2 所示，r*为间距比参数，表示硬化参数p'm与临界状态平均有效应力p'cs之间的比值；n为应力-状态参数，控制土的屈服面形状；p'和q分别为土的平均有效应力和偏应力。

图2 r* = 3 时不同n 值情况下的 CASM 模型屈服面形状Fig.2 Yield surface shape of CASM with different n values when r* = 3

在CASM 模型中，Yu 建议用基于Rowe 剪胀方程[23]的塑性势函数描述土的塑性变形方向，表达式为：

式中：G(p',q,β)为土的塑性势函数；β表示塑性势函数的大小，可由p'、q值计算得到。根据式（3）可得：

式中：H为塑性模量；和dσ'j分别为土的塑性应变增量和有效应力增量，i或j=r、θ、z。

1.3 材料的应力应变关系

饱和土的弹性变形服从广义胡克定律，应力应变关系为：

将式（4）与式（6）相加，整理后可得到CASM 模型的弹塑性应力应变关系为：

式中：dεi为土的应变增量，i=r、θ、z；dσ'i（或dσ'j）为土的应力增量，i或j=r、θ、z。

2 不排水柱孔扩张半解析解

2.1 柱孔扩张弹性解

不排水柱孔扩张时，土的体应变dεv= dεr+ dεθ+ dεz和竖向应变dεz均为0。并且饱和土的纯弹性变形不产生超孔隙水压力（Δu= 0）。根据式（1）、（6）可解得弹性区的应力解[8]为：

式中：σ'rp和rp分别为弹塑性交界面处土的径向有效应力和弹塑性区的半径；ure为弹性区土的位移。

2.2 柱孔扩张弹塑性解

2.2.1 土体应力计算式在求解弹塑性区内土体应力时，Chen 等[8]的方法需要在孔周弹塑性区内每个计算点上，根据土的总应变量分别进行差分求解，使得计算效率不高，且土中孔隙水压力的求解必须等待上述所有计算点上的土体应力全部求出以后，才能用式（1）进行积分计算，不能直观反映土中孔隙水压力在孔径扩张时的动态变化。为此，本文引入辅助变量ξ，通过一系列坐标转换，在拉格朗日坐标系中建立以ξ为自变量，适用于孔周任一土质点上有效应力和孔隙水压力计算的一阶常微分方程组。与Chen 等[8]的方法相比，本文方法更高效，所得结果也可直观反映孔周土应力和孔隙水压力在柱孔扩张时的变化。

在孔周弹塑性区内，土体发生大变形，用对数应变表示土的径向应变εr和环向应变εθ，表达式[8]为：

式中：ξ为辅助变量，ξ=urp/r= (r-r0)/r，urp为孔周弹塑性区内某点土的径向位移。在式（12）中，以ξ为自变量对εr、εθ取微分，然后将所得dεr和dεθ的表达式及dεz= 0 一起代入式（7），可得：

式中：c11=1-µ2+Ehµbzaθ+Ehµazbθ+Ehazbz+Ehaθbθ；c12=-Ehar(bθ+µbz)+µ(1+µ-Ehbθaz+Ehazbz)；c21=-Ehar(aθ+µaz)+µ(1+µ-Ehaθbz+Ehazbz) ；c22=1-µ2+Eharbr+Ehµarbz+Ehµbraz+Ehazbz；c31=-Ehbr×(µaθ+az)+µ(1+µ+Ehaθbθ-Ehbθaz)；c32=µ+µ2+Ehµarbr-Ehbθaz-Ehµ]arbθ-Ehµbraz；Ψ =(1+µ)×[1-µ-2µ2+Eh(1-µ)(arbr+aθbθ+azbz)+Ehµ(aθbr+bθar+azbθ+bzaθ+azbr+bzar)/E；ai=∂F/∂σ′i，bi=∂G/∂σ′i，i=r、θ、z。

在式子ξ=urp/r中令ξ对r求导，结合式（12），可得：

durp/dr=1-exp(εr)=1-1/(1-ξ)式中：为土质点位移urp对r的空间导数；dr为孔周任意相邻两个土质点之间的径向距离。根据式（1）、式（13）和式（14），可以解得：

式（13）和式（16）分别为弹塑性区内基于拉格朗日描述的土体有效应力和孔隙水压力求解方程式，初始条件为σ'r(ξp)、σ'θ(ξp)、σ'z(ξp)和u(ξp)，ξp对应土质点刚开始发生塑性变形时的ξ；超孔隙水压力Δu=u(ξ) –u0。

2.2.2 边界条件正常固结土的初始状态为式（13）和式（15）的初始条件。对于超固结土，根据式（2）、式（10），可得：

式中：q(ξp)=M[(ln(Rp′m0)-ln(p′0))/lnr∗]1/n；R=p'C/p'm0为表示土体超固结程度的参数[8]；p'C为土体历史上的最大硬化程度；p'm0为土体在当前应力条件下对应虚拟的硬化程度。

2.2.3 计算结果的转换由式（13）和式（16）求解得到的σ'r、σ'θ、σ'z和u均是关于辅助变量ξ的拉格朗日描述。为便于分析，须将计算结果变换为关于径向位置r的欧拉描述。

从ξp到ξ对式（14）进行积分，可以得到径向位置r与辅助变量ξ之间的关系式为：

从ξp到ξa（孔壁处的ξ值）对式（14）进行积分，可以得到扩孔结束后的弹塑性区半径rp为：

3 算例分析

3.1 参数分析

以饱和伦敦黏土为例，分析应力-状态参数n和间距比r*对饱和土不排水柱孔扩张结果的影响。根据文献[18]，伦敦黏土的临界状态参数为：Γ= 2.759，λ= 0.161，κ= 0.062，μ= 0.3，M= 0.888，φ'cs= 22.75°，正常固结土和超固结土的静止侧压力系数分别为 1-sinφ和为用土体原位竖向应力定义的土的超固结比）。土的初始体积v0按下式计算：

式中：Γ为p'=1.00 kPa 时土的体积；λ为土的等向压缩系数；φ'cs为土的临界内摩擦角。

3.1.1 应力-状态参数n针对R= 1.0 和4.0 的两种伦敦黏土，计算参数如表1 所示，土中不排水柱孔扩张结果分别如图3、4 所示。

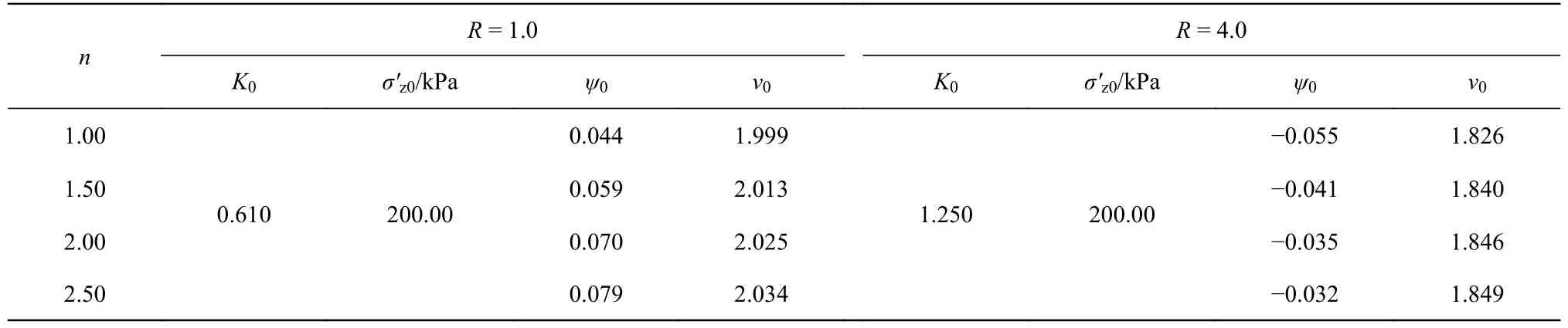
表1 r＊ = 3.00 时不同n 值的伦敦黏土初始参数Tab.1 Initial parameters of London clay with different n values when r* = 3.00

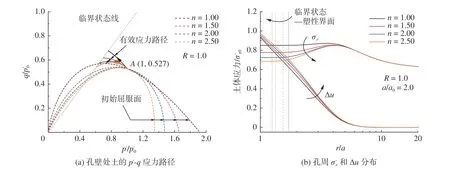
图3 不同n 值时正常固结伦敦黏土（R = 1.0）中的柱孔扩张结果Fig.3 Results of cavity expansion in normally consolidated London clay (R = 1.0) with different n values

图4 不同n 值时超固结伦敦黏土（R = 4.0）中的柱孔扩张结果Fig.4 Results of cavity expansion in overconsolidated London clay (R = 4.0) with different n values

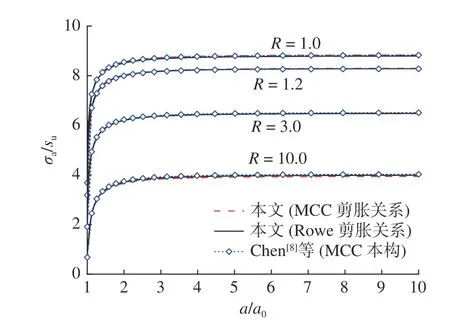
如图3(a)、4(a)所示，当n值不同时，土的屈服面形状和相应的不排水应力路径也不同；4 种n值时的正常固结土在柱孔扩张过程中均表现为硬化，而超固结土则均表现为软化；结合表1 可知，由于同样初始应力条件下两种固结程度饱和土的初始体积v0均随着参数n的增大而增大，相应不排水应力路径终点处的p'、q值将随n的增大而减小。如图3(b)、4(b)所示，参数n的取值对孔周σ'r和Δu的分布有较大影响：孔壁附近的σ'r均随n的增大而减小，并且孔周围临界状态区的半径也随n的增大而减小；正常固结土中扩孔所得Δu随n的增大而增大，而超固结土中的Δu在孔壁附近（1.0≤r/a≤1.5）随n的增大而减小，在较远区域（1.5

3.1.2 间距比r*针对R= 1.0 和4.0 的两种伦敦黏土，计算参数如表2 所示，土中不排水柱孔扩张结果分别如图5、6 所示。

表2 n = 2.00 时不同r＊情况下的伦敦黏土初始参数Tab.2 Initial parameters of London clay with different r* values when n = 2.00

图5 不同r*值时正常固结伦敦黏土（R = 1.0）中的柱孔扩张结果Fig.5 Results of cavity expansion in normally consolidated London clay (R = 1.0) with different r* values

图6 不同r*值时超固结伦敦黏土（R = 4.0）中的柱孔扩张结果Fig.6 Results of cavity expansion in overconsolidated London clay (R = 4.0) with different r* values

如图5(a)、6(a) 所示，参数r*的不同取值使饱和土具有不同的屈服面形状和不排水应力路径；结合表2 可知，同样初始应力条件下土的初始体积v0随r*的增大而增大，因此饱和土不排水应力路径终点处的p'、q值随r*的增大而减小；4 种r*值情况下的正常固结土在柱孔扩张过程中均发生硬化，而超固结土则在r*= 2.00、3.00、4.00 时发生软化，在r*= 5.00 时发生硬化，这是因为r*值的增加使土的初始状态从临界状态线的下方移动到了上方（表2 中状态参数ψ0从负值变为正值），进而使土的硬化行为发生了改变。如图5(b)和6(b)所示，参数r*的取值对孔周的σ'r和Δu分布有较大影响：孔壁附近的σ'r值和临界状态区的半径随r*的增大而减小，Δu随n的增大而增大。

3.2 不同模型结果比较

选取BBC（Boston blue clay）黏土作为案例进行柱孔扩张计算，并将所得结果与文献[8]中基于修正剑桥模型（MCC）的结果进行对比，用以验证本文方法的合理性与创新性。BBC 黏土的基本力学参数为Γ=2.759，λ= 0.150，κ= 0.030，ν= 0.278，M= 1.200，不同R值情况下的BBC 黏土其余计算参数如表3 所示。CASM 模型中的屈服面参数取n= 1.65、r*= 2.00，此时用CASM 模型计算得到4 种BBC 黏土的初始孔隙比与使用MCC 模型时的计算结果相同。另外，本文在使用CASM 模型进行计算时，还分别使用了两种不同的剪胀关系，Rowe 剪胀关系和MCC 剪胀关系（塑性势函数与MCC 模型的屈服函数相同），进而可以分析土的剪胀关系改变对柱孔扩张结果的影响。为了对比需要，本节计算得到的所有土体应力均使用土的不排水剪切强度su进行量纲归一化。

表3 BBC 黏土的计算参数Tab.3 Calculation parameters for BBC clay

图7、8 分别给出了在4 种BBC 黏土中不排水柱孔扩张时，归一化扩孔压力σa/su和孔壁处超孔隙水压力Δu/su随扩孔孔径a/a0的变化。可以发现，无论使用哪一种剪胀关系，基于CASM 模型的计算结果都与基于MCC 模型的基本一致，说明若选择合适的屈服面参数n、r*，本文解答可近似计算修正剑桥类黏土在不排水柱孔扩张时的应力变化。

图7 归一化的扩孔压力随孔径的变化Fig.7 Variation of normalised internal cavity pressure with cavity radius

图8 归一化的孔壁超孔隙水压力随孔径的变化Fig.8 Variation of normalised excess pore pressure at cavity wall with cavity radius

图9 给出了4 种BBC 黏土中不排水柱孔扩张a/a0= 2.0 时，孔周围σ'r、σ'θ和σ'z的分布。可以看到，3 种方法计算所得不同R值饱和土的σ'r、σ'θ和σ'z在孔壁附近均为定值，说明土体达到了临界状态。对于正常固结土（R=1.0）和中等超固结土（R= 1.2、3.0），当使用MCC 剪胀关系时，本文方法所得σ'r/su、σ'θ/su和σ'z/su与文献[8]的在孔周3 个区域内均吻合；当使用Rowe 剪胀关系时，所得结果与文献[8]的在临界区和弹性区内吻合，在弹塑性区存在一些小的差异。对于严重超固结土（R= 10.0），文中分别使用两种剪胀关系所得孔周土体应力分布在临界状态区和弹性区内与文献[8]的结果吻合，在弹塑性区内存在差异，并且本文所得孔周的弹塑性区半径明显小于文献[8]的，这主要是因为两种本构模型中屈服面函数的形状不同所致。图10 给出了n= 1.65、r*= 2.00 时CASM 模型中的屈服面与同样硬化参数时MCC 模型中的对比。可以发现，CASM 模型的屈服面在临界状态线的下方与MCC 模型吻合较好，但在临界状态线的上方低于MCC 模型，这使得同样初始条件的严重超固结土（R= 3.0、10.0）在CASM 模型中初始屈服时的偏应力q要小些，因此更为合理[16]。

图9 a/a0 = 2.0 时孔周围径向、环向和竖向有效应力分布Fig.9 Radial, tangential and vertical effective stress distributions around the cavity with a/a0 = 2.0

图10 CASM 模型和MCC 模型的屈服面形状对比Fig.10 Contrast of yield surface shapes in CASM and MCC

3.3 实例应用

使用Lehane[24]在弱超固结Bothkennar 黏土中的压桩试验对本文解答的可靠性进行验证。场地内从地下2 m 到7 m，土的超固结比Roc从2.00 降为1.46，静止侧压力系数K0,OC从0.650 降为0.500，有效竖向压力σ'z0从25.50 kPa 增加到54.80 kPa，均近似为线性增长或减小；土的有效内摩擦角均值为35.50º，计算可知Mc= 1.430；土的压缩系数Cc= 0.5，回弹系数Cs= 0.033，换算得到λ= 0.217、κ= 0.015；地下水位的埋深为2 m。如图11(a) 所示，按照Yu[18]中给出的方法，使用正常固结Bothkennar 黏土的不排水剪切应力路径来近似确定n、r*，得到n=2.00、r*= 2.50。