基于熵值图的多功能雷达工作模式识别
2024-03-11温珍银孙闽红唐向宏田煦然郁春来
温珍银,孙闽红,唐向宏,田煦然,郁春来
(1.杭州电子科技大学通信工程学院,浙江 杭州 310018;2.空军预警学院,湖北 武汉 430019)
0 引言
随着电子对抗环境日益复杂和雷达技术的不断发展,现代雷达的多功能化越来越显著,特别是多功能雷达(MFR)拥有庞大、稳定的信号库,可以有序贯地执行大量不同的任务,并能灵活地调整信号参数来变换工作模式以实现战术目的。多功能雷达发射信号参数的敏捷性、适应性和重叠性使得对其工作模式识别越来越具有挑战性,如何从快速捷变的信号参数中提取出可靠有效的信息来推断和识别MFR的当前状态,对后续情报分析和干扰决策具有重要意义[1]。
目前,对于MFR工作模式的识别方法主要分为有监督和无监督的方法[2]。对于有监督的方法,文献[3]通过构建雷达信号特征库,并运用DS证据理论进行多域信息融合实现雷达工作模式的判定;文献[4]通过构造信号级加参数级样本数据用于卷积神经网络进行雷达行为辨识;文献[5—6]结合句法模式理论将雷达信号脉冲序列由低向上建立雷达语义层次模型,利用有限状态机或数据关联方法对雷达工作模式进行推理;文献[7]设计了一种工作模式序列的时间序列表示,并提出了一种序列长短期记忆网络的脉冲级识别框架对工作模式进行识别;文献[8]提出一种雷达模式的多信息源识别和学习框架,通过从参数范围、功能指标、数据规律三个维度提取特征,实现非特定雷达的模式识别。文献[9]融合先验知识与原型网络对小样本条件下的MFR工作模式进行识别。
对于无监督的工作模式识别方法,文献[10]引入生物序列分析技术将雷达信号规律重建为任务序列,提出一种序列比对的搜索模式识别算法;文献[11]通过分析雷达行为状态与脉冲信号参数间的映射关系,利用主成分分析法提取特征参数,再结合改进的C-均值聚类算法实现雷达行为状态的分类;文献[12]将随机动力系统建模思想与MFR层次模型相结合,提出了一种预测状态表示模型的MFR工作模式识别方法;文献[13]提出了一种用于工作模式分类的无监督时间序列聚类方法,该方法在不使用任何标记数据的情况下对发射器脉冲序列进行分割和聚类。
在实际应用中,MFR工作模式多种多样,其发射波形复杂且快速捷变,上述对MFR工作模式的识别方法主要存在两点不足:一是受限于动态表征算法的能力和特定场景限制,提取的特征难以反映MFR的运行规律;二是仿真条件过于理想化,在进行工作模式识别时的样本数据中仅包含单一的工作模式,这是不合理的,实际场景中接收到的脉冲信号往往包含多种工作模式混合的情形。
为解决上述不足,本文首先提出基于小波变换的多功能雷达状态切换点检测方法,然后,基于近似熵[15]、样本熵[16]、模糊熵[17]和排列熵[18]提出新的熵值图特征,并结合卷积神经网络实现对MFR工作模式的智能识别。
1 基础知识
1.1 多功能雷达脉冲序列分析
MFR具有显著的智能和灵活性,能够根据不同的战术目的适时地改变工作模式、波束方位、脉宽和脉冲重复间隔等信号波形参数,其在不同状态下信号参数的实时改变为MFR状态切换的检测及工作模式识别提供了依据。在雷达系统资源调度下,将MFR在某一段时间内实现的不同功能状态映射到脉冲上,可以得到其发射的脉冲序列形式[19]如图1所示。

图1 多功能雷达脉冲序列形式Fig.1 The form of multi-functional radar pulse sequence
图1中每一个线条代表一个发射脉冲的脉冲描述字(pulse description word,PDW),线条的长短和颜色只是为了区分脉冲信号参数的不同,并不代表实际脉冲参数的变化。可以看到MFR脉冲序列由一系列具有一定时序规律和逻辑关系的连续脉冲组构成,每个脉冲组由组内各脉冲之间的时间排列和脉冲特征参数构成,不同的雷达工作模式对应不同排列规则的脉冲序列组,各序列组内脉冲参数也存在捷变,同时在不同雷达状态下的参数也有各自的变化规律[1]。
对于侦察接收到某一MFR发射的n个脉冲信号,提取每个脉冲的载频、脉宽、幅度、脉冲重复间隔和占空比参数组成PDW,则接收的MFR脉冲序列可以用如下向量表示:

(1)

1.2 熵值分析
近似熵、样本熵、模糊熵和排列熵都是用来表征信号序列复杂性和度量信息不确定性的无量纲指标,熵值越大代表信号序列越复杂和随机,适用于处理非线性问题。由于MFR信号参数快速捷变同时在不同工作模式下具有各自的参数变化特点,因此在本文中,通过提取这几个熵特征值来表征工作模式下某一参数的变化规律以及复杂程度。
1.2.1近似熵
近似熵是一种用于衡量信号序列波动规律的参数,反映了信号序列的复杂性,近似熵值越大对应的信号序列成分越复杂和无规律,越小则说明信号序列越规则。
给定n点时间信号序列x={x1,x2,…,xn},将序列按顺序组成m维模式向量u(1),u(2),…,u(n-m+1),其中u(i)=[xi,xi+1,…,xi+m-1],1≤i≤n-m+1。定义两个模式向量u(i)和u(j)之间差值的极大值为距离
(2)
(3)
对所有模式向量u产生的Cm(r)取对数再取平均值
(4)
在m+1维度上,重复上述步骤可以得到φm+1(r),从而求出序列的近似熵:
A(m,r)=φm+1(r)-φm(r)。
(5)
1.2.2样本熵
样本熵是基于近似熵的一种改进方法,具有更好的抗干扰性和稳定性,是当前运用比较广泛的一种熵特征值计算方法。样本熵值越大,对应的信号序列越混乱,序列取值越复杂和随机。样本熵值越小,则该信号序列越稳定规律,信号序列自相似性越高。

(6)

(7)
1.2.3模糊熵
近似熵和样本熵都是通过度量信号序列在维数变化时新模式产生的概率大小来衡量复杂性,但是二者中两个向量的相似性都是基于Heaviside二值函数而定义的,而实际情况中各类样本边缘之间通常比较模糊,导致在度量复杂度时对应的熵值突变性较大,在近似熵和样本熵的基础上,利用模糊集理论提出了模糊熵的方法。模糊熵计算过程如下:

模糊熵中两模式向量的距离与近似熵的含义相同但不包含i=j的情况,即
(8)
再利用式(9)模糊函数来度量X(i),X(j)的相似度。
(9)
式中:r为相似容限,l为梯度,一般取整数2或3。
则类似近似熵可以定义函数:
(10)
在m+1维度上,重复上述步骤可以得到φm+1(l,r),从而求出序列的模糊熵:
F(m,l,r)=lnφm(l,r)-lnφm+1(l,r)。
(11)
与近似熵和样本熵的物理意义相似,模糊熵也是评价信号序列前后部分之间的重复性及混乱程度的。模糊熵值越大,信号序列成分越复杂,不确定性越高,新模式出现的概率越大。
1.2.4排列熵
排列熵是一种检测序列随机性和动力学突变的方法,也是用于度量信号序列复杂程度的指标,其引入了排列的思想,具有抗噪性能良好和计算简单等优点。
给定模式维数m,延迟参数τ(τ>0),对时间序列x进行空间重构得到一组m维向量:
Yj=[xj,xj+τ,…,xj+(m-1)τ],(1≤j≤n-(m-1)τ)。
(12)
将Yj的m个分量xj,xj+τ,…,xj+(m-1)τ按数值大小从低到高进行排序,共有m!种排列方式,将排列次序相同的重构分量进行统计,根据出现个数计算每一个重构分量排列情况出现的概率:
(13)
式中:K为重构分量Yj的排列方式的数量。
由香农熵的定义可以得到序列x={x1,x2,…,xn}的排列熵为
(14)
可以用排列熵的大小来表示信号序列的随机程度,评价信号序列数据周期性和随机性。其中H(m)越大,信号序列越复杂无序,反之H(m)越小,对应的信号序列越平稳有序。
2 基于熵值图的多功能雷达工作模式识别
考虑实际电子侦察系统截获到的雷达信号往往包含多个工作模式,若将未经状态分割的雷达信号直接作为样本进行工作模式识别将导致较大的结果误差,因此在工作模式识别之前首先对雷达脉冲信号进行状态切换点检测并切割。其次在电磁环境复杂的情况下,侦收到的信号存在漏脉冲和虚假脉冲的情况,这两种情况与后续工作模式识别准确率有极大的关联,因此必须对接收到的原始雷达脉冲序列进行预处理以消除漏脉冲和虚假脉冲的影响并归一化后才能进行工作模式识别。本文采用文献[6]提出的方法对漏脉冲和虚假脉冲进行处理。整个工作模式识别流程如图2所示。

图2 本文工作模式识别流程Fig.2 Working mode recognition process in this paper
2.1 多功能雷达状态切换点检测
小波变换是一种将时域信号转换为频域信号提取特征的方法[20],具有多分辨分析的特点,能够较好地表达出信号序列中的突变和非平稳部分。在信号出现突变时,通过小波变换得到的细节系数可以集中在某一尺度上从而确定突变时间段,因此使用小波变换来分析和检测一个信号函数的奇异点(突变点)具有很好的效果[21-23]。
首先定义雷达工作模式切换点:对于MFR在时刻t时的脉冲,若其PDW某一维的参数与上一时刻脉冲的该参数有较大变化,则认为此参数在该脉冲时刻存在突变,若PDW所有的参数都存在突变,则该脉冲时刻的突变可认为是MFR工作模式切换的表现,即切换点。
考虑到多功能雷达不同工作模式之间存在参数重叠,且同一工作模式内也存在信号参数变化的问题,若仅对脉冲单一参数进行切换点检测并不可靠,如在图3中若仅对PRI参数进行切换点检测,则会检测出许多工作模式内的虚假切换点,为了避免单维脉冲参数序列上虚假切换点的干扰,本文将对漏、虚假脉冲处理后的脉冲序列的多维参数进行综合检验。将多功能雷达脉冲序列看成是多维时间序列,采用多维时间序列分析的方法进行分析[24],首先在每一个独立维度上分别确定突变点,然后通过显著性比较或投票等策略选择切换点作为整个多维时间序列最终的突变点。

图3 不同工作模式下脉冲序列部分参数变化图Fig.3 Partial parameter variation diagram of pulse sequence under different working modes
基于小波变换的多功能雷达状态切换点检测算法流程如下:
步骤1 取预处理后的MFR脉冲序列S=(P1,P2,…,Pi,…,Pn)中的RF参数进行离散多辨小波4层分解,再重构生成近似系数和细节系数,取第一层细节系数d1。
步骤2 设定一个固定的滑动窗口,沿着第一层细节系数从序列开始以固定的滑动步长滑动到结束。

步骤4 对序列S中的PA,PW,PRI和DC参数依次重复步骤1-步骤3得到TPA,TPW,TPRI,TDC。
步骤5 对TRF,TPA,TPW,TPRI,TDC进行多维综合比较得到该MFR状态的切换点集合Γ=(Γ1,Γ2,…,Γv),v为切换点的个数。
最后依据得到的雷达状态切换点对雷达脉冲序列进行分割得到不同工作模式下的雷达脉冲子序列S′。
2.2 熵值图构建
进行工作模式识别的关键一步是提取出合适的特征,特征的好坏直接关系到工作模式的识别效果。MFR可以在不同工作模式之间进行灵活切换,虽然每种工作模式下的波形参数具有快速捷变的特点,但是不同工作模式的信号参数存在一定的变化规律,依据这一特性,本文参照时间序列分析方法,通过提取不同工作模式下脉冲序列各参数的多种熵值来表征不同工作模式下各参数的变化情况,再转换为熵值特征图并通过神经网络进行识别。
通过提取到PDW序列每一个维度参数的近似熵、样本熵、模糊熵和排列熵后可以得到一个5×4的熵值矩阵,并将其定义为熵值图,用W表示为
(15)
将这个矩阵存储并通过灰度化处理后以图片形式保存,用于后续的分类识别。图4—图6展示了本文仿真实验产生的每种工作模式在不同场景下随机选择某一脉冲序列经过熵值提取后构建的熵值图特征,其中参数误差均为5%,具体脉冲参数见表1。

表1 各工作模式下的脉冲参数范围Tab.1 Pulse parameter range in each working mode

图4 虚假脉冲率为20%时,随机生成的4种工作模式脉冲序列的熵值图Fig.4 Entropy maps of four randomly generated working mode pulse sequences with a false pulse rate of 20%

图5 漏脉冲率为20%时,随机生成的4种工作模式脉冲序列的熵值图Fig.5 Entropy maps of four randomly generated working mode pulse sequences with a leakage pulse rate of 20%

图6 漏、虚假脉冲率同时为20%时,随机生成的4种工作模式脉冲序列的熵值图Fig.6 Entropy maps of four randomly generated working mode pulse sequences with the leakage and false pulse rates are both 20%
从图4—图6中可以看出,在不同场景下同种工作模式的熵值图特征有相似的特性,但不同工作模式的熵值图特征具有明显的差异。根据MFR的波形运用机理,MFR在执行不同的战术任务时通过灵活地改变信号参数及变化规律来转变工作模式,而提取参数序列的熵值可以反映不同工作模式下该参数的复杂程度和变化情况。因此,基于多维参数熵值构建的熵值图特征能很好地表征各工作模式下信号波形的参数组合变化规律和时序规则,反映了MFR在不同功能任务下的特点,可以表征不同工作模式之间的差异。
最后,选择卷积神经网络(CNN)进行工作模式识别,CNN具有内部提取深度特征的优势,在图像处理领域被广泛应用。将不同的熵值图特征送入CNN中进行空间特征提取,尽可能将熵值图内工作模式隐含的参数变化规律特征全面提取,识别算法流程如图7所示。

图7 基于熵值图特征的工作模式识别流程Fig.7 Working mode recognition process based on entropy map features
3 仿真实验与分析
3.1 实验参数设置
为了验证本文方法的有效性,根据文献[25]中关于机载MFR工作模式的介绍及参数特征分析,建立跟踪、搜索、搜索+跟踪和边搜索边跟踪这4种工作模式的脉冲参数模型如表1所示,在漏脉冲率及虚假脉冲率为0%,参数误差为5%时,部分工作模式参数变化情况如图8所示。

图8 四种工作模式参数变化图Fig.8 Parameter variation diagram of four working modes
基于多次实验测试得到的小波变换切换点检测算法相关最优实验参数如表2所示。

表2 切换点检测算法参数Tab.2 Switch point detection algorithm parameters
仿真实验使用的CNN网络结构含有3层卷积层,每一层均作最大池化处理,之后连接3层全连接层,同时添加dropout层防止训练时过拟合,激活函数为softmax,选用均值平方差损失函数和Adam优化器,学习率为0.000 1。训练过程中batch size为64,训练轮数为1 000。
3.2 训练集与测试数据集
依据表1中工作模式参数范围,基于Matlab软件平台模拟仿真产生包含4种工作模式在内共计19次工作模式切换的脉冲序列500组,随机选择300组进行训练,剩余样本用于测试。考虑实际工作中,雷达接收脉冲信号受电磁环境和参数估计误差的影响,对PW,PA,RF,PRI等参数分别设置5%~10%,步长为1%的估计误差,同时在参数误差为5%时产生虚假脉冲、漏脉冲及混合误差分别为0%,5%,10%,15%,20%,25%的脉冲序列,混合误差表示为漏脉冲、虚假脉冲同时存在的情况。雷达脉冲序列经过预处理和状态切换点检测后,提取工作模式子序列熵值图特征送入卷积神经网络中识别,对本文方法进行测试评估和分析。
3.3 实验结果与分析
实验一 基于小波变换的多功能雷达状态切换点检测
本实验在3.2节仿真产生的数据集下进行,其中在漏脉冲率及虚假脉冲率为0%,参数误差为5%时,随机选择仿真产生的某一雷达脉冲序列对应的工作模式脉冲位置如表3所示。在3.1节的实验参数设置下,对仿真产生的多工作模式脉冲串序列进行切换点检测性能测试,以表3的雷达脉冲序列为例,脉冲序列中各工作模式切换点位置检测结果如表4所示。
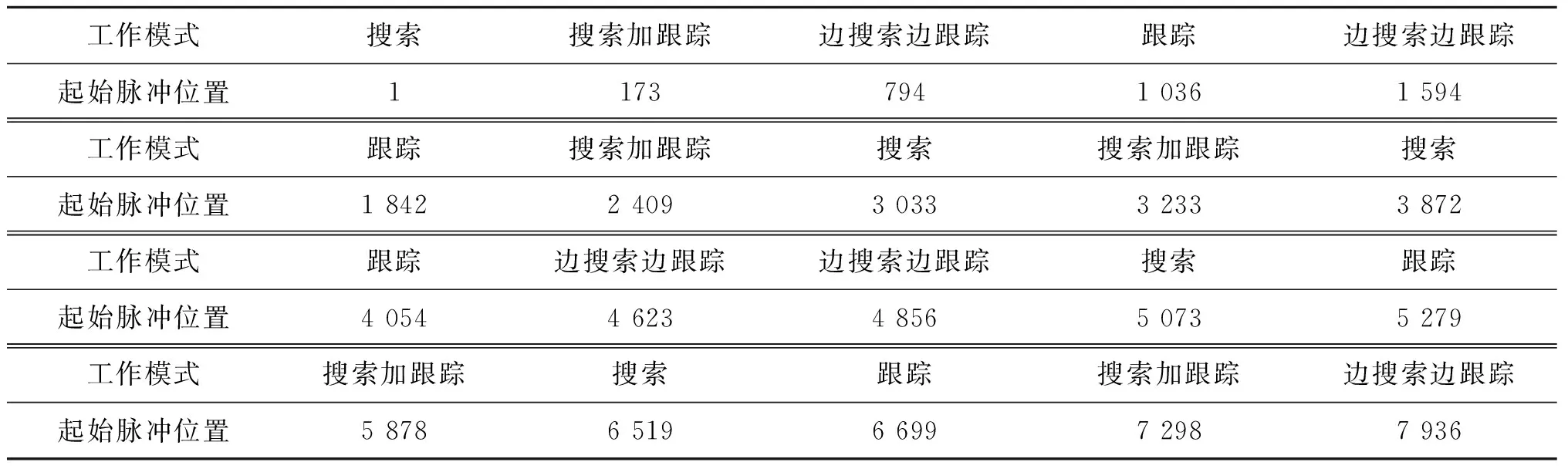
表3 漏脉冲率及虚假脉冲率为0%,参数误差为5%时某一雷达脉冲序列对应的工作模式Tab.3 The working mode corresponding to a radar pulse sequence when the leakage pulse rate and false pulse rate are 0% and the parameter error is 5%

表4 漏脉冲率及虚假脉冲率为0%时的各工作模式下切换点检测结果Tab.4 Detection results of switching points in various operating modes when the leakage pulse rate and false pulse rate are 0%
由表4可以看出共有2个工作模式切换点未被检测出来,同时检测出1个虚假切换点,但是对比表3可以看到在第4 856个脉冲前后一段时间的脉冲序列都是边搜索边跟踪模式,因此第4 856个切换点是连续发射同一个工作模式两次的分割点,实际上并未发生工作模式切换。所以对于该脉冲序列只有一个工作模式切换点未被检测出来,其检测正确率为94.5%。
随后考虑在不同误差场景下测试切换点检测算法性能,本文使用正确检测率和虚假检测率来衡量状态切换点检测算法的性能。其中,正确检测率RTR表示实际检测到的真实切换点个数(nT)与总切换点个数(nall)之比:
(16)
虚假检测率QFR表示检测到并不存在的切换点个数(nF)与总切换点个数(nall)之比:
(17)
不同漏脉冲、虚假脉冲和参数误差情况下,多工作模式脉冲串序列切换点检测性能如图9—图11所示。
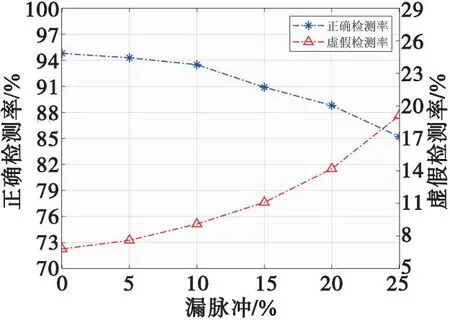
图9 不同漏脉冲场景下切换点检测性能图Fig.9 Performance chart of switching point detection in different leakage pulse scenarios

图10 不同虚假脉冲场景下切换点检测性能图Fig.10 Performance chart of switching point detection in different false pulse scenarios
由图9—图11可以看出,基于小波变换的雷达状态切换点检测方法能够对多工作模式组合的脉冲序列进行有效检测,漏脉冲率和虚假脉冲率在10%以下时正确检测率能够达到93%,虚假检测概率不超过10%;在虚假脉冲率或漏脉冲率为25%时的正确检测率能够在85%左右。对于参数误差在10%时,状态切换点正确检测率趋近80%,并且随着参数误差的增大正确检测率迅速下降,虚假检测率大幅提高,这是由于随着参数误差的增大使得参数存在较大变化从而将参数真实的突变点淹没,导致状态切换点未能被正确检测,并且检测出许多虚假状态切换点。在虚假脉冲率或漏脉冲率大于15%时虚假检测率迅速提高,这是因为在状态切换点检测之前对脉冲序列的漏脉冲和虚假脉冲处理方法效果不佳,脉冲序列中仍存在较多的虚假脉冲和漏脉冲从而影响状态切换点的正确检测。
实验二 基于熵值图的多功能雷达工作模式识别
利用2.2节中熵值图特征的构建方法,将经过状态切换点检测并分割后的雷达脉冲序列进行参数熵值提取并构建熵值图特征,然后送入到训练好的网络中进行评估测试。同时,为了更好地体现本文方法的优越性,在同等仿真实验参数条件下,将本文方法与文献[25]基于特征融合和深度稀疏置信网络的方法和文献[26]基于多层建模和边际化堆栈降噪自动编码器的方法进行对比,在不同场景下4种工作模式的识别性能如图12所示。
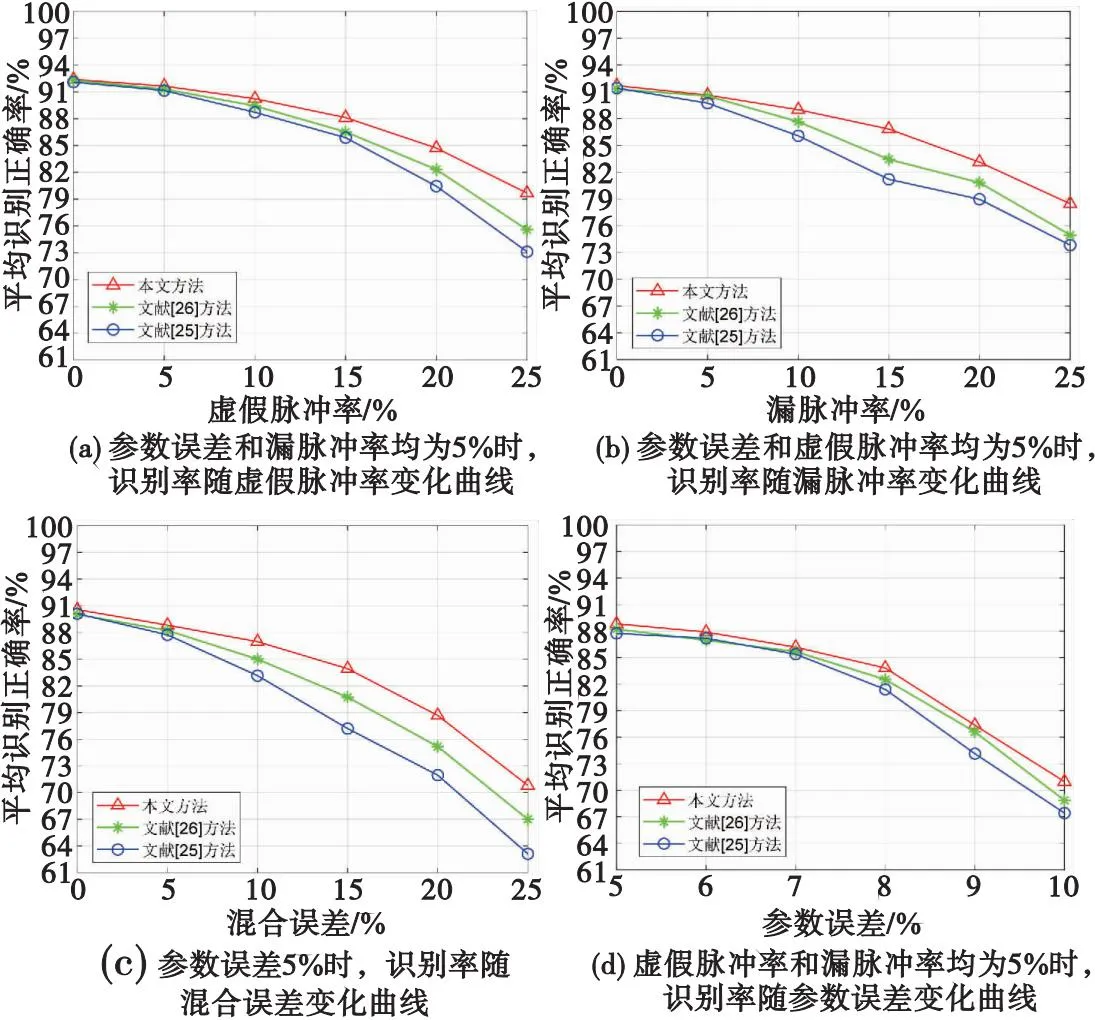
图12 不同场景下工作模式识别实验结果图Fig.12 Experimental results of working mode recognition in different scenarios
图12的实验说明了本文提出的基于熵值图的MFR工作模式识别方法在各种复杂环境下仍有较高的识别准确率,且性能优于对比文献的方法。在经过变化点检测并切割后的4种工作模式平均识别率在参数误差、漏脉冲率为5%,虚假脉冲率为20%时接近85%;在参数误差、虚假脉冲率为5%,漏脉冲率为20%时识别率为83.1%;同时在参数误差为5%、混合误差为15%时平均识别率能达到83.9%。当虚假脉冲率和漏脉冲率为25%时,识别效果低于80%,这是由于在漏脉冲率和虚假脉冲率较高时,状态切换点检测方法将检测出许多虚假切换点,导致脉冲序列分割不准确,分割后的某一段脉冲序列可能包含两种工作模式脉冲片段,因此识别效果较差。
同时还考虑了工作模式识别效果随参数误差的变化情况,如图12(d)所示,在虚假脉冲率和漏脉冲率均为5%时,识别正确率在参数误差为8%时接近84%。但是随着参数误差的逐渐增大,识别准确率迅速下降,这是由于当参数误差增加时,脉冲序列的参数存在较大变化,导致状态切换点检测效果不佳同时参数变化规律发生改变,从而影响识别效果。
本文所提的熵值图特征充分利用了工作模式中脉冲参数的变化特点,将多参数的复杂变化规律与工作状态关联起来,能够达到更好的识别效果。由图12可以看出,本文方法在漏脉冲、虚假脉冲和参数误差的情况下均比对比文献的方法具有更好的抗误差性能和更出色的识别效果,平均识别准确率均有一定的提升。
4 结论
针对多功能雷达的信号参数复杂多变,工作模式灵活变化的情况,本文提出了一种基于小波变换的多功能雷达状态切换点检测算法,实现对多工作模式组合的脉冲序列进行状态切换点检测,并将其分割成只含单一工作模式的脉冲序列,为后续工作模式识别提供可靠的数据;并根据多功能雷达不同工作模式参数的时序变化特点,提出了一种基于熵值图的工作模式识别方法,首先提取脉冲信号各参数序列的熵值特征,然后构建该工作模式下的熵值图,并送入卷积神经网络中进行训练和识别。实验结果表明,本文方法在虚假脉冲率或漏脉冲率为25%时,不同工作模式之间的切换点检测正确率接近85%左右;工作模式识别正确率在虚假脉冲为20%时接近85%,在漏脉冲为20%时能达到83.1%,在参数误差为8%时接近84%,识别性能均优于两种对比文献方法,验证了本文算法的有效性。本文仅对某机载多功能雷达的4种工作模式进行了识别,对于更多较为复杂的雷达工作模式还需进行研究;同时,在变化点检测算法中并未对一个或多个参数突变时导致工作模式切换的情形进行探讨,这将在后续进一步研究;此外,本文在训练和测试阶段均仿真了充足的样本,因此如何在小样本条件下进行工作模式识别也是今后需要研究的方向。
