爆炸冲击波集合分解排列熵时变峰值降噪算法
2024-03-11杜桂云崔春生杨志飞刘双峰
杜桂云,崔春生,杨志飞,刘双峰
(1.中北大学省部共建动态测试技术国家重点实验室,山西 太原 030051;2.中北大学电气与控制工程学院,山西 太原 030051)
0 引言
爆炸冲击波压力属于典型的非平稳、非线性的随机信号,其特点是上升沿陡峭、带宽宽、超压峰值高、正压时间短[1]。爆炸冲击波的杀伤破坏作用主要取决于冲击波的超压峰值ΔP,比冲量I+和正压作用时间τ+[2]。同时,这3个参数也是衡量弹药爆破及杀伤的重要指标,可以为武器研制过程中的爆炸过程中的威力对比及其性能评估提供重要的依据[3]。
由于爆炸冲击波测试受高温环境、磁场干扰、测试设备等原因的影响存在误差,实测冲击波信号中会混有大量环境噪声及系统自身的高频噪声。为减弱上述因素的影响,对实测冲击波数据进行降噪处理成为爆炸冲击波信号处理中的重要环节。处理非平稳信号最常用的是小波分析[4]、经验模态分解(EMD)[5]、变分模态分解(VMD)[6]等方法。小波分析是一种成熟且广泛使用的降噪算法,该算法在时频域都可以表征局部信号,能较好地保持信号的细节,但是在降噪过程中,小波基和分解层数的选择、阈值的选取准则、阈值函数的设计,都会对最终的信号去噪效果产生很大的影响。文献[7]对爆炸冲击波信号进行小波阈值去噪后,虽去噪效果明显,但小波分解去噪的效果过度依赖小波基及软硬阀值的选取。EMD是一种能够自适应分解非线性、非平稳信号的方法[8],该方法无需先验信息就能凸显信号的物理特性,但在理论上缺乏严格的数学证明,存在严重的模态混叠、端点效应等问题。变分模态分解(VMD)是一种完全非递归变分模态分解模型,可以很好地抑制EMD方法的端点效应问题[9],但其去噪结果易受分解层数和惩罚因子的限制。完全集合经验模式分解(complete ensemble empirical mode decomposition,CEEMDAN)算法重构误差很小,消除了添加噪声对信号的影响[10]。文献[11]通过CEEMDAN抑制了EMD算法中存在的模态混叠问题,同时有效去除了信号的高频噪声。
针对上述问题,本文提出了基于集合分解的排列熵时变峰值爆炸冲击波降噪算法。
1 基本原理
1.1 CEEMDAN算法
CEEMDAN算法通过在EMD的每个阶段添加自适应白噪声,允许在少量平均次数内实现微小的重构误差[11]。这种处理方式有效地抑制了模态混淆,并确保了原始信号的完整性。它也解决了EEMD算法中的噪声残留问题,同时提升了计算效率。具体步骤如下:
1) 在原始数据X(t)中分别多次添加自适应白噪声Zq(t),q表示添加噪声次数,本文取q=100,则第q次信号可表示为Xq(t)=X(t)+aqZq(t)(q=1,2,…,100),其中aq为第q次加入白噪声的标准差。CEEMDAN的一阶IMF分量为
(1)
2) 构造新的待分解信号X(t),X(t)=R1(t)+aqZq(t),进行到100次分解,得到CEEMDAN的二阶IMF分量:
(2)
余项R2(t)=X(t)-IIMF2。
3) 重复步骤1)和步骤2),直到程序终止,共产生m个IIMF,最后的余项为
(3)
1.2 排列熵算法
排列熵(permutation entropy,MPE)是一种判断信号复杂度的指标[12],能够检测信号的突变性和随机性。与样本熵[13](SE)只能检测一维时间序列的复杂度相比,MPE可以从不同的尺度上来评估信号的复杂性和随机性。而爆炸冲击波信号在不同尺度均包含重要信息,因此MPE更适用于爆炸冲击波信号分析。具体计算步骤如下:
1) 对时间序列X={x1,x2,…,xh}进行多尺度粗粒化处理:
(4)
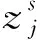

N=(h/s-(n-1)t),
(5)
(6)
式中:n为嵌入维数,t为时间延迟。
3) 计算排列熵:
(7)
式中:Pj为第j次符号出现的概率。
4) 对式(7)计算的排列熵进行归一化处理。参考文献[14],将排列熵阈值设置为0.6,大于或等于的IMFs分量需要进行降噪处理。
(8)
1.3 时变窗长时频峰值滤波算法
时变窗长时频峰值滤波(time-varying window length time frequency peak filtering algorithm, TVWTFPF)算法[15]采用置信区间交叉准则来获得最优窗长,从而估计得到瞬时频率。TVW算法具体步骤如下:
1) 对于原始信号x(t),将其编码为解析信号y(t):

(9)
2) 采用PWVD算法[16]对其进行频率估计
(10)
式中:f为频率,h(λ)为窗函数。
3) 求出瞬时频率对应的置信区间。
(11)

4) 当置信区间满足置信区间交叉准则时,求得该时刻的最优窗长h*。
5) 求出在最优窗长h*下所对应的瞬时频率值,最后估计得到重建信号:
(12)
2 基于集合分解的排列熵时变峰值爆炸冲击波降噪算法
2.1 算法实现
基于集合分解排列熵时变峰值爆炸冲击波降噪算法是一个涵盖信号分解、含噪分界点分析、去噪处理和重构的全面的降噪处理流程,它巧妙地结合了CEEMDAN算法、MPE分析和TVWTFPF算法,逐步且精确地将噪声从爆炸冲击波信号中去除,以重建出清晰、准确的冲击波信号。步骤如下:
1)使用CEEMDAN 算法将爆炸冲击波信号按从高到低频率分解为有限个IMF分量(IMF1,IMF2,…,IMFn)与1个残基。每个IMF代表不同的频率分量。低阶IMFs对应有效信号或噪声的尖锐部分,高阶IMFs对应信号的低频部分。
2)通过计算IMFs的多尺度排列熵(MPE)分析含噪分界点。MPE值大小代表时间序列的随机性和复杂程度,值越接近1,随机性越强,非平稳程度越高。
3)使用TVWTFPF算法对需去噪的IMFs分量进行降噪处理。该方法将IMFs分量调制成单位幅值的解析信号,然后对解析信号进行瞬时频率估计,提取每个时刻在最优窗长下的频率峰值作为该时刻的瞬时频率估计值从而恢复有效信号,实现爆炸冲击波信号的去噪。
4)重构经过处理的IMFs分量和有效IMFs分量。
该算法流程如图1所示。

图1 基于集合分解的排列熵时变峰值爆炸冲击波降噪算法流程Fig.1 Algorithm flow for noise reduction of explosive shock waves based on ensemble decomposition with time-varying peak values of arrangement entropy
2.2 含噪模型建立及分析
2.2.1建立含噪模型
冲击波超压值随时间变换的规律可采用修正的Friedlander公式,可采用衰减系数α,超压峰值采用Sadovskii经验公式,正压作用时间采用TNT爆炸冲击波正压时间修正公式。
修正的Friedlander 公式:
(13)
(14)
Sadovskii超压峰值经验公式:
(15)
正压时间拟合公式:
(16)
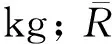
近地爆炸时冲击波传播规律与半无限空中爆炸情况类似,爆炸能量一部分被地面吸收,另一部分被反射到空中,当装药在地面爆炸时炸药质量相当于原来的2倍并乘以对应材料系数。故马赫反射区地面测点的理论超压值根据式(5)进行转换。
ΔPM=ΔP(1+cosφα)。
(17)
依据上述公式,构建比例距离为1.02,2.04,3.07 m/kg1/3的冲击波信号含噪模型,其中,P0=0.101 3 MPa,η=1,如图2所示。

图2 冲击波信号含噪模型Fig.2 Noise model of shock wave signal
2.2.2降噪效果评价方法
本文引入了信噪比(SNR)和均方根误差(RMSE)作为评价指标来衡量信号降噪效果。信噪比用于衡量信号与噪声的比值,均方根误差用于衡量过滤后的信号与原始信号的紧密程度,SNR和RMSE用于说明去噪算法的性能。其计算公式如下:
(18)
(19)
式中:X为原始信号,Y为降噪后的信号,n为信号的序列长度。一般情况下,降噪后信号SNR越大、RMSE越小,降噪效果越好。但降噪效果不仅要考虑评价指标,还要考虑降噪算法对信号超压峰值、正压时间等信号特征的影响较小。
3 算例分析
3.1 含噪模型实验及分析
分别采用Bessel低通滤波、CEEMDAN滤波、基于集合分解的排列熵时变峰值爆炸冲击波降噪算法(以下简称TVWTFPF滤波)对文中构建的含噪模型进行去噪。其中,Bessel 低通滤波阶数选择6,截止频率为40 kHz,利用将含噪信号分解成若干个IMFs分量,利用MPE分析选取前5个IMFs分量进行滤波。而TVWTFPF滤波根据置信区间交叉准则选择最优窗长。
从表1、表2中可以看出:经3种降噪方法处理后各模型的SNR指标从高到低分别为TVWTFPF滤波、CEEMDAN滤波、Bessel低通滤波。其中,TVWTFPF降噪方法处理的信噪比提升比例最高,与原始含噪模型相比增加了15.58,14.47,14.36 dB;RMSE指标中,TVWTFPF滤波后的RMSE是最低的,与原始含噪模型相比降低了147.24×10-4,36.96×10-4,1.60×10-4。

表1 3种降噪法与含噪模型SNR指标对比Tab.1 Comparison of SNR indicators between three noise reduction methods and noisy models

表2 3种降噪法与含噪模型RMSE指标对比Tab.2 Comparison of RMSE indicators between three noise reduction methods and noisy models
以1.02 m/kg1/3模型为例,研究以上3种降噪方法对毁伤评估参数的影响,见表3。Bessel低通滤波、TFPF滤波降噪后的超压峰值较模型值的误差率分别为3.69%,0.93%,0.47%;正压时间较模型值的误差率分别为2.72%,0.99%,0.30%;TVWTFPF降噪算法对毁伤评估指标的影响最小。
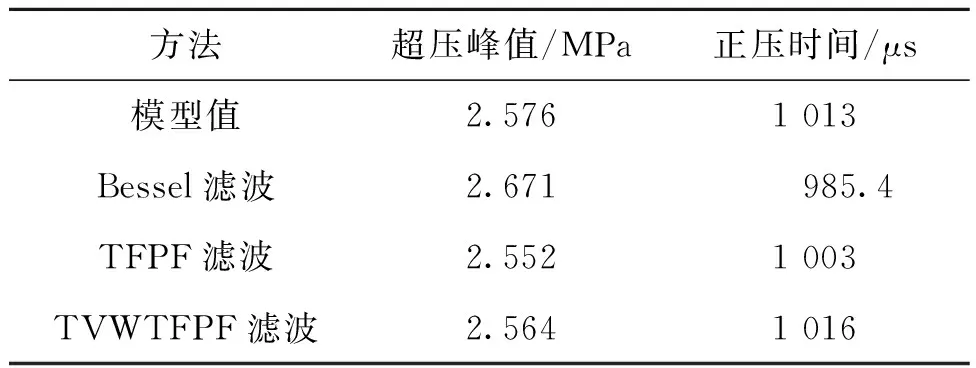
表3 3种降噪法对毁伤评估参数的影响Tab.3 Impact of three noise reduction methods on damage assessment parameters
3.2 实测数据验证
实测冲击超压信号来自某60 kg级TNT爆炸冲击波试验,取1.02 m/kg1/3实测冲击波信号进行降噪处理,信号经CEEMDAN分解的部分分量如图3所示,该模型各个IMF分量的排列熵值如图4所示,由此判断噪声分类点。将该模型的降噪结果图绘制于图5中,3种降噪方法频域对比如图6所示,并在表4列出3种降噪方式后的实测冲击波超压峰值、正压作用时间等参数。
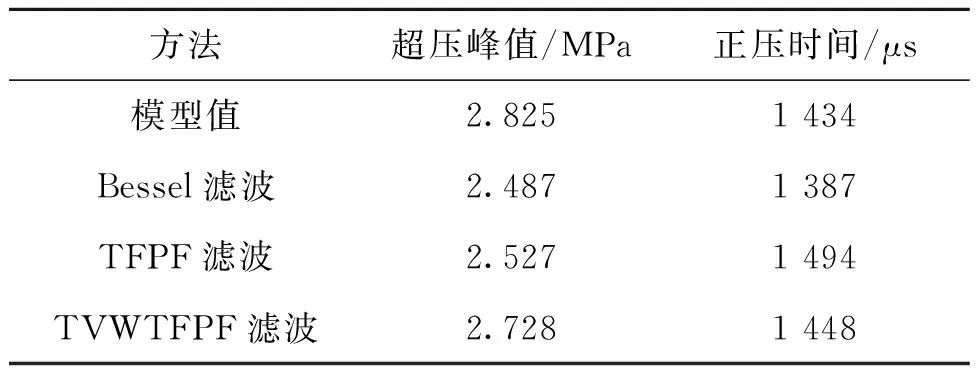
表4 3种降噪法对1.02 m/kg1/3实测信号毁伤评估参数的影响Tab.4 Impact of three noise reduction methods on the damage evaluation parameters of 1.02 m/kg1/3 measured signal

图3 1.02 m/kg1/3CEEMDAN分解IMFFig.3 1.02 m/kg1/3CEEMDAN decomposition IMF
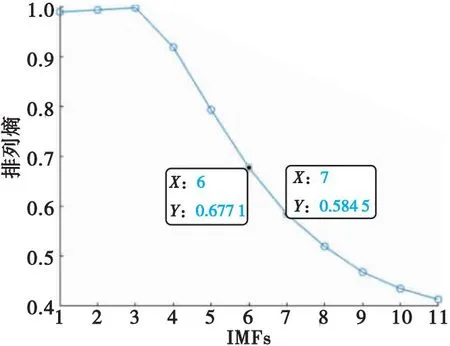
图4 1.02 m/kg1/3IMF分量的排列熵Fig.4 Arrangement entropy of 1.02 m/kg1/3 IMF components

图5 3种降噪方式对比Fig.5 Comparison of Three Noise Reduction Methods

图6 3种降噪方法频域对比Fig.6 Frequency domain comparison of three noise reduction methods
对比分析3种降噪方法,Bessel滤波后信号出现了明显的相位失真,而且原始信号中存在的尖峰、突变等重要信息丢失;CEEMDAN滤波虽然能抑制失真问题,但是低频有效信息未能很好地保留;而本文所提的方法既能去除冲击波信号中的噪声,又尽可能地保留有效信息。从毁伤评估参数来看,TVWTFPF对毁伤评估指标的影响最小。综上所述,基于集合分解的排列熵时变峰值爆炸冲击波降噪算法与原始信号的重合度高,对实际工程具有重要的指导意义。
4 结论
本文提出了基于集合分解的排列熵时变峰值爆炸冲击波降噪算法,通过构造不同比例距离下的含噪冲击波信号模型和实测数据验证了算法的可行性。利用CEEMDAN将原始数据按频率由高到低分解成一系列IMFs,再通过计算这些IMF分量的样本熵,确定需滤波模态分量和保留分量的分界线,将需要进行降噪的分量进行TVWTFPF处理,再将处理后的分量和原始剩余分量求和得到最终信号。该算法不仅能有效降噪,而且降噪后的波形与原始波形的相似度最高,有效地保留了原始冲击波信号包含的局部信息,经理论模型和实测数据验证,以1.02 m/kg1/3模型为例,在理论模型中与原始含噪模型相比,TVWTFPF算法的SNR值提高了15.58 dB,RMSE值降低了147.24×10-4。在实测数据中,TVWTFPF算法的SNR值提高了13.21 dB,RMSE值降低了133.43×10-4。本文算法在3种算法中表现最优,而且对毁伤评估参数的影响最小。综上,本文提出的冲击波数据降噪方法,展示了显著的实用性,为爆炸冲击波信号处理这一领域的研究提供了有益参考,并且具有广阔的实际应用前景。
