压阻式加速度传感器动力学响应分析与验证

张洁宇,石云波,赵 锐,闫晓朋

(1.中北大学电子测试技术重点实验室,山西 太原 030051)

(2.山西北方机械制造有限责任公司,山西 太原 030013)

为保证高冲击环境测试信号的真实、准确,高量程加速度传感器的抗高过载能力设计至关重要。高量程压阻式加速度传感器的封装体呈现为多自由度结构,其动力学响应分析多集中在其动态行为描述、特性捕捉及参数辨识[1]等方面,而与加速度传感器的直接关联则较少。王川等[2]通过集中参数法建立了压裂车多体耦合动力学模型,并对其进行耦合振动仿真分析,研究了各参数对系统振动的影响。毛君等[3]将橡胶输送带压陷阻力试验台简化为三自由度动力学模型,对其进行动力学特性分析。Scutaru等[4]根据多自由度模型对受机械振动影响下的复杂弹性系统动力减振器进行了设计与验证。本文针对压阻式加速度传感器经过灌封后的复杂封装体结构,基于多自由度系统理论,分析其在受迫振动下的动力学响应过程,并通过冲击试验进行验证。

1 封装体结构动力学响应分析与验证

1.1 封装体结构动力学响应分析

本文以四端固支细梁结构的压阻式加速度传感器为例,加速度传感器量程为50 000g,灵敏度为0.323 μV/g,传感器整体封装结构示意图如图1所示。可以看出,当加速度传感器受到冲击时,管壳内灌封胶、贴片胶、玻璃基底和敏感结构互相作用,将底端固定面看作管壳内部与贴片胶、灌封胶接触面,由于灌封胶将贴片胶、玻璃基底和敏感结构都密封包裹在管壳内,因此将灌封胶与各层设定为并联关系,将贴片胶、玻璃基底和敏感结构设定为串联关系,封装体结构的振动模型设定为多自由度的串并联振荡系统,建立的封装体结构多自由度系统等效示意图如图2所示。

图1 传感器封装结构示意图

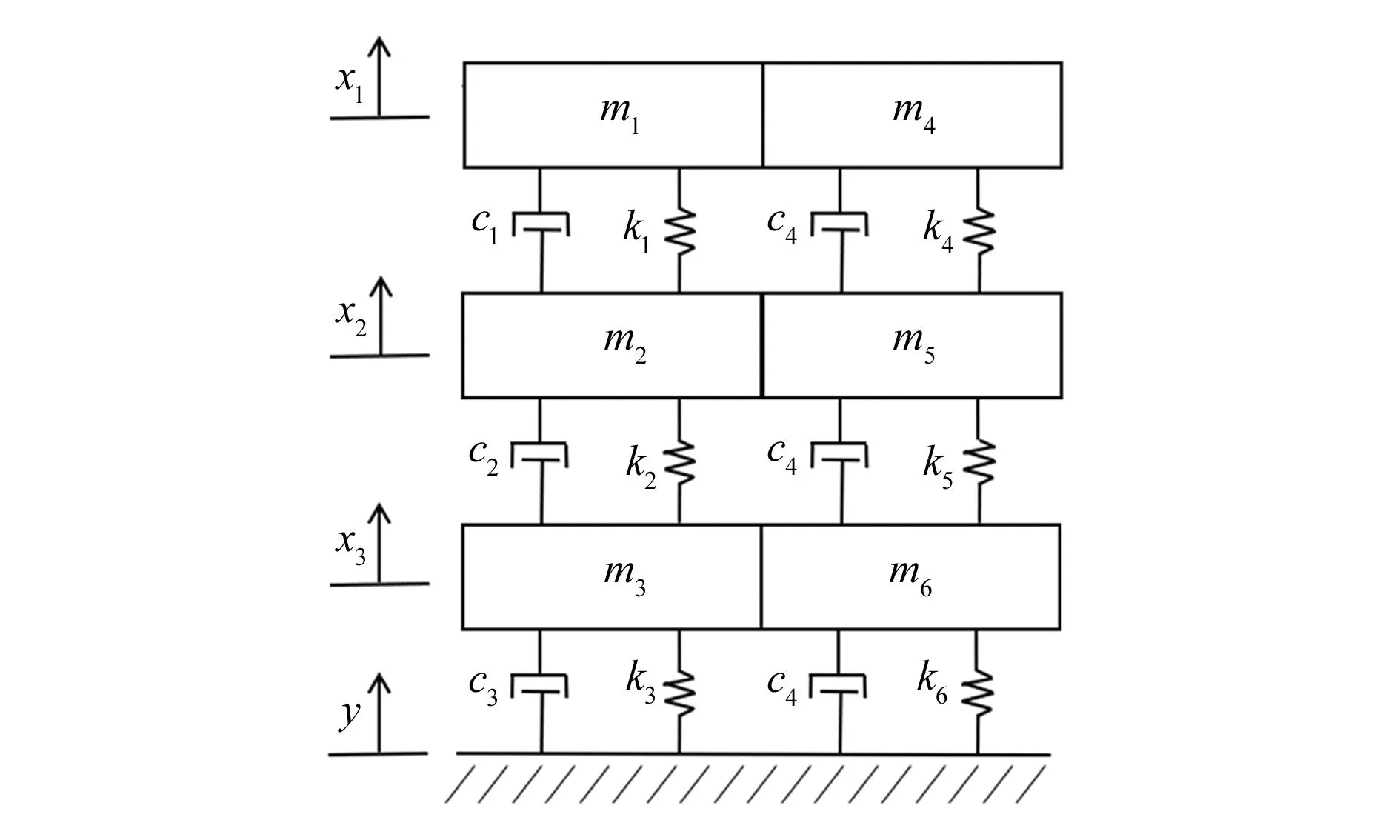
图2 封装体结构多自由度系统等效示意图

图中,m1、m2、m3分别为梁-质量块、玻璃基底、贴片胶的等效质量,m4、m5、m6分别为梁-质量块、玻璃基底、贴片胶对应的灌封胶的等效质量,c1、c2、c3、c4分别为梁-质量块、玻璃基底、贴片胶和灌封胶的阻尼系数,k1、k2、k3分别为梁-质量块、玻璃基底、贴片胶的等效弹簧刚度,k4、k5、k6分别为梁-质量块、玻璃基底、贴片胶的灌封胶等效弹簧刚度,x1、x2、x3、y分别为梁-质量块、玻璃基底、贴片胶和管壳受冲击下的位移。

研究封装体结构中敏感结构上梁-质量块的位移随时间t的变化关系,需要考虑梁-质量块与玻璃基底、灌封胶之间,玻璃基底与贴片胶、灌封胶之间,以及贴片胶与灌封胶之间的相互作用关系,根据等效系统模型,结合达朗贝尔原理(D'Alembert principle)列出系统的振动方程[5]:

(1)

令

(2)

式中:a(t)为传感器受冲击载荷下的加速度曲线。

在霍普金森杆对加速度传感器动态校准试验中,通过多普勒测试得到的冲击脉冲曲线如图3所示,在动力学响应分析中,可将其看作一个半正弦脉冲,因此封装体结构受冲击载荷作用下的加速度表达式为

(3)

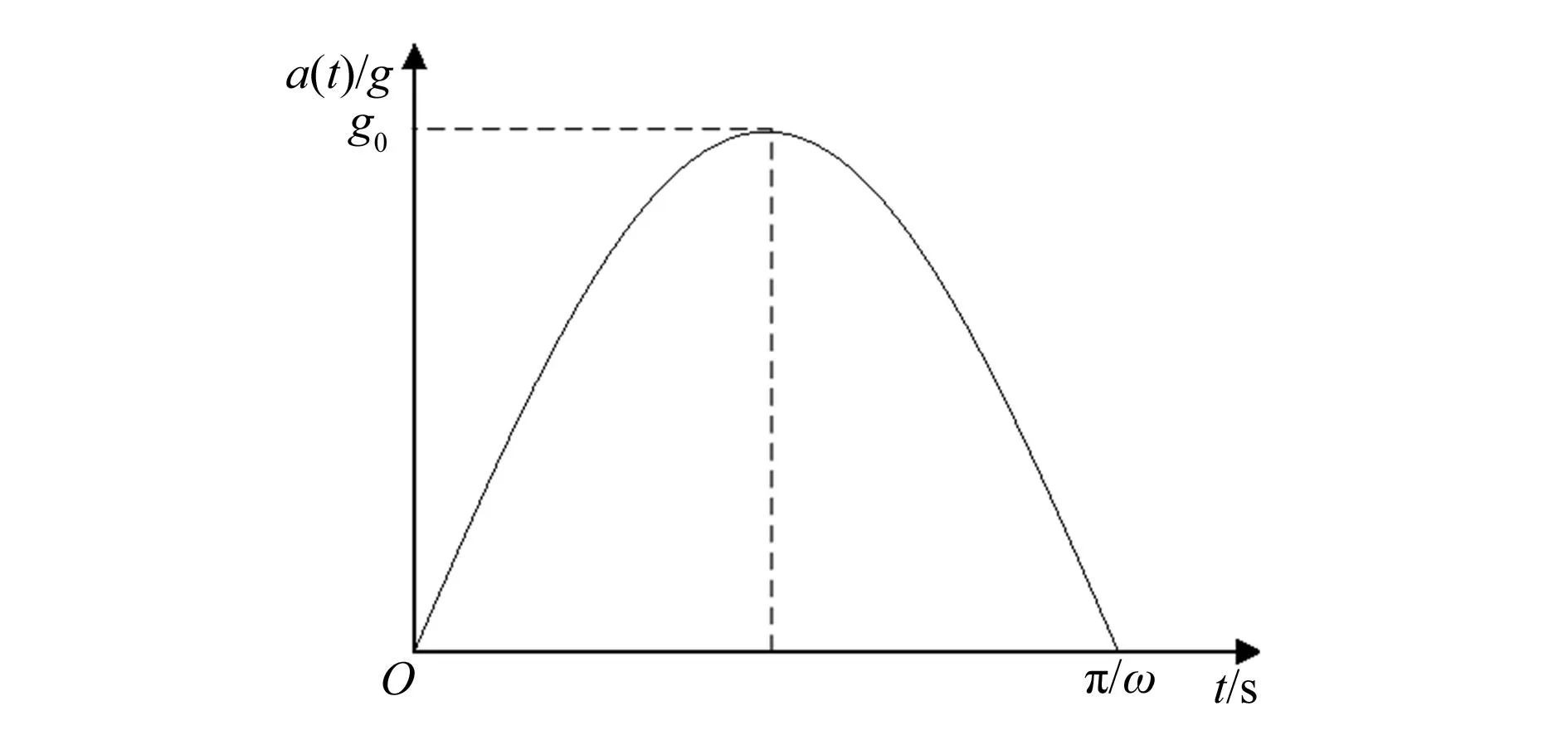
图3 半正弦脉冲曲线

式中:g0为加速度幅值,ω为角频率。

本文主要研究冲击载荷下敏感结构的位移响应情况,即受迫振动下梁-质量块的位移。

令

(4)

写成矩阵形式:

(5)

令

(6)

式中:A0为冲击载荷幅值,φ为冲击载荷相位。

(7)

采用矢量法[6]对矩阵进行求解,设此方程组的特解为

(8)

式中:A1、A2、A3分别为梁-质量块、玻璃基底与贴片胶的位移幅值,j表示虚部。

对于位移的解取复数虚数部分,将式(8)代入式(5)解得

(9)

将式(9)代入式(8)即可得到受迫振动下各等效质量块的时间-位移关系式。

1.2 传感器测试信号解算

对于四端固支的压阻式加速度传感器,其输出电压取决于电桥上压敏电阻变化,当受到惯性力作用时,电桥上相邻电阻变化趋势相反,相对电阻变化趋势相同,假设压敏电阻在四梁上位置、扩散浓度、受力大小完全相同,此时输出电压Uo可表示为

(10)

式中:Ui为输入电压,π44为硅剪切压阻系数,σ1、σt分别为压敏电阻受冲击下纵向应力与横向应力。

由应力应变关系及纵向应变与横向应变之间的关系可将式(10)转化为只与纵向应变ε1有关的方程,因此加速度计输出电压与梁上压敏电阻所受应变的关系为

(11)

式中:E为弹性模量,μ为泊松比。

图4 梁上压敏电阻处冲击变形简化

结合式(11)和压敏电阻变形可得

(12)

将加速度传感器敏感结构简化为图5所示的两端固支结构,梁-质量块上x位置处的挠度w计算公式为

(13)

图5 均布载荷下梁-质量块模型受力等效图

式中:q为敏感结构所受荷载,l、b、h分别为梁的长、宽、高,l2为质量块长度,惯性矩I=bh3/12,集中力F=ql2。根据式(13)可得荷载q,从而解算得到冲击载荷下传感器敏感结构位移最大值。

2 动力学响应模型验证

由第1节可以看出通过矢量法化简后得到的矩阵表达式中参数较多,求解得到的梁-质量块、玻璃基底和贴片胶的位移响应结果较复杂,且计算量大,求解较困难。引入MATLAB数学软件,凭借计算机强大高效的运算能力,通过调用各参数的方式来实现各阶方程的计算。

2.1 传感器校准测试信号验证

用霍普金森杆测试系统对压阻式加速度传感器进行冲击试验,测试系统如图6所示,将加速度传感器固定在入射杆末端的安装座上,调节气泵气压,当弹丸撞击霍普金森杆的一端时,在杆中产生一个向杆另一端传播的应力波,当应力波到达加速度传感器与安装座的接触面时反射为拉伸脉冲,当压缩脉冲与拉伸脉冲叠加会在安装界面产生静拉力,使安装座与传感器飞离杆端,此时激光多普勒设备和加速度传感器测得的信号发生变化,通过采集卡保存到PC机进行数据解算处理,得到加速度传感器测得的加速度数据和其敏感结构位移响应结果。

图6 霍普金森杆测试系统

对压阻式加速度传感器在量程范围内进行5次冲击试验,通过实测加速度传感器数据分别验证动力学响应模型,以其中一组数据为例,分别解算激光多普勒设备和加速度传感器实测数据,得到过载加速度曲线,如图7所示,多普勒测得冲击载荷峰值为36 843.4g,脉宽为27.45 μs。

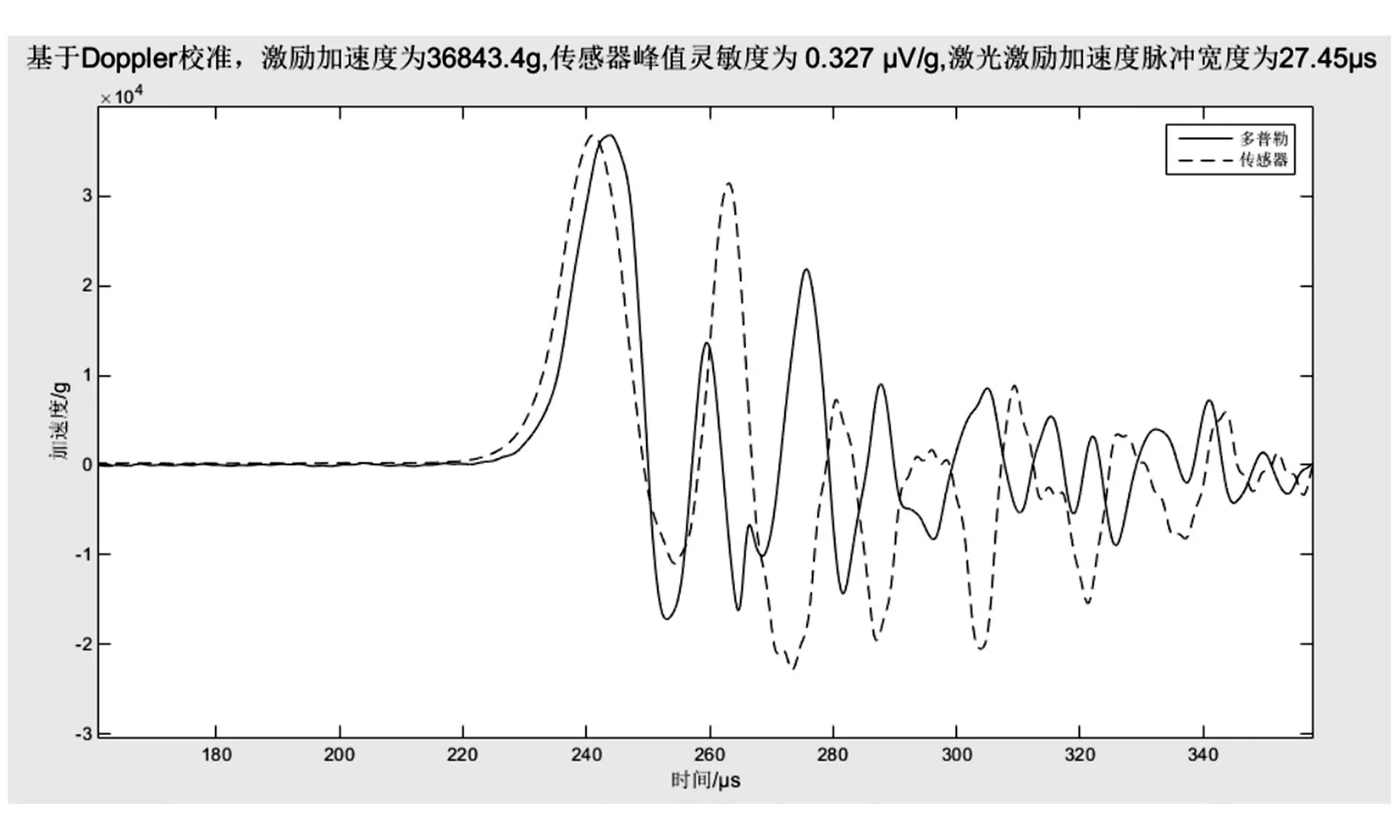
图7 传感器测试数据图

提取冲击载荷下传感器的时间-输出电压数据进行解算,得到敏感结构梁-质量块的时间-位移曲线,如图8所示,位移最大值为0.033 8 μm。

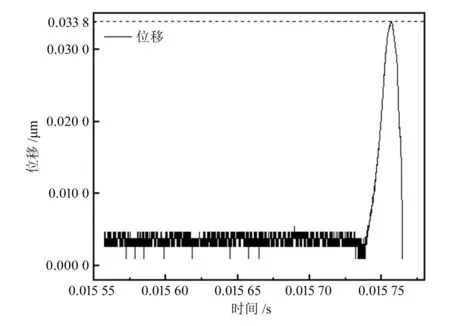
图8 试验解算时间-位移曲线

2.2 基于MATLAB的动力学响应模型数值计算

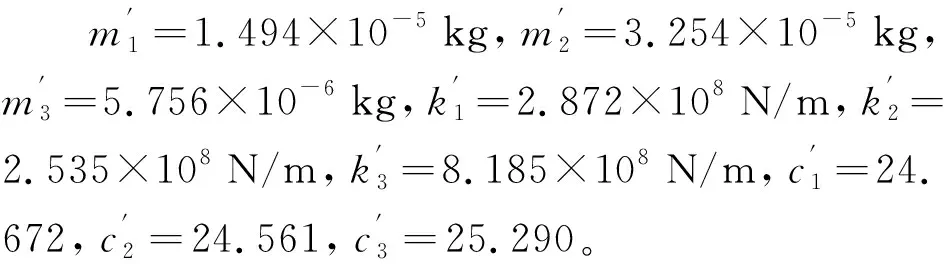
将多普勒实测获得的冲击过载输入MATLAB编译的响应模型,通过数值计算,可得到相同加速度峰值和脉宽过载环境下加速度传感器敏感结构的时间-位移响应曲线,如图9所示。理论位移最大值为0.036 8 μm,与通过实测数据解算得到的位移最大值对比,误差为8.88%。

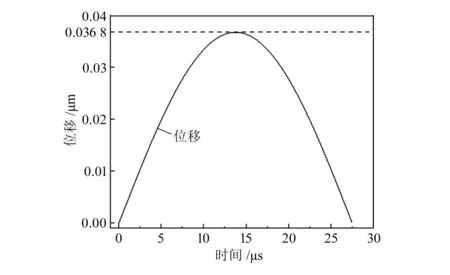
图9 MATLAB计算时间-位移曲线

2.3 数值计算与试验对比分析

为进一步验证响应方程的准确性,通过解算实测获得的5组试验数据,分别得到加速度传感器敏感结构的实际位移和多普勒测得的冲击载荷,将多普勒测得的不同冲击峰值和冲击脉宽的过载加速度输入 MATLAB编译的响应模型中,通过数值计算得到加速度传感器敏感结构的理论位移,与解算得到的实际位移进行对比分析。由表1可知,加速度传感器的响应模型理论位移与实测获取的试验位移的误差均小于10%,可以有效表征加速度传感器在冲击载荷下的位移响应过程,进而为加速度传感器的优化设计提供可靠参考。

表1 响应方程与试验结果对比

3 结束语

本文通过分析压阻式加速度传感器封装体结构的动态响应过程,并对比理论与试验结果,表明动力学响应模型可以较好地实现对多自由度结构在受迫振动下的位移响应分析。针对压阻式高量程加速度传感器,已构建的多自由度动态响应模型可为其高量程提升及封装结构优化等提供理论指导与工程参考。

考虑到实际封装过程中管壳内灌封胶形状并不规则,灌封胶相关参数具有一定误差,因此后续需要加强加速度传感器封装的过程控制,对现有转接板外形进行规则化改进,从而提升封装工艺精度。