SMA解锁装置设计与分析

王 讯,关世玺,张孟轲

(中北大学航空宇航学院,山西 太原 030051)

武器装备中有各种用于连接结构分离如弹头与载体末级分离、火箭级间分离等的解锁装置[1],目前这类解锁机构多为火工装置,虽然技术比较成熟,但可靠性低、稳定性差,造成的污染让精密仪器产生很大的误差[2]。非火工装置的优势是低冲击、无污染[3],目前主要以形状记忆合金(shape memory alloys,SMA)驱动的解锁装置居多。美国国家航空航天局曾开发了一种由SMA管驱动的解锁装置[4],但该装置所需驱动力大、解锁时间长且同步性较差;Huang等[5]设计了一款SMA丝解锁装置,虽然SMA丝的触发时间短,但提供的驱动力小[6]。本文设计了一种SMA丝驱动的两级直推式分瓣螺母解锁装置,两级解锁可以大大减小SMA丝所需的驱动力。

1 结构设计

本文设计的SMA丝解锁装置如图1所示,为最大尺寸不超过φ54 mm×70 mm的圆柱体。装置主要由承载机构、解锁机构和壳体组成,其状态包括锁紧和分离。锁紧时,螺栓20和分瓣螺母19配合,将被连接件1与上端盖2压紧,分瓣螺母在径向使用一级钢球18与支撑环4进行约束,驱动弹簧3产生的推力一部分与一级钢球18作用在支撑环4上的静摩擦力平衡,另一部分与二级止动球8作用在支撑环上的力平衡,触发块13与二级止动球8被压紧,记忆合金丝11处于未通电状态。解锁时,形状记忆合金丝11通电产生回复力,拉动触发块13向下移动直到二级止动球落入触发块的凹槽,这时支撑环的平衡被打破,驱动弹簧产生竖直向下的推力推动支撑环向下运动,直到一级钢球落入支撑环球窝,此时螺栓和分瓣螺母之间的预紧力解除,由涡卷弹簧14产生转动力矩,在转动盘6和直动盘16的凹槽导向下作用到支撑手上产生径向推力,推动分瓣螺母19径向移动,完成分离。

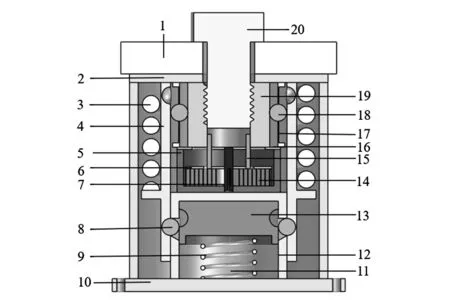
1—被连接件;2—上端盖;3—驱动弹簧;4—支撑环;5—撑开器壳

2 驱动单元设计

SMA解锁装置的驱动单元主要由驱动弹簧、涡卷弹簧、安全弹簧和SMA丝组成。对整个装置分析可知,驱动单元是整个解锁装置的关键,因此需对驱动单元进行详细的设计。

2.1 Brinson本构关系

SMA具有非线性以及参数的多变性,用简单的数学公式很难准确地表述其力学行为。目前工程上常用的描述SMA特性的模型有Tanaka模型、Liang-Rogers及Brinson模型[7],它们都采用马氏体体积百分数ξ来描述SMA的相变过程。其中Brinson模型用应力诱发马氏体体积分数ξS与用温度诱发马氏体体积分数ξT的和代替ξ[7],这更加符合真实工况,用于工程计算具有较高的准确性。本文选用SMA在受控回复边界条件下的Brinson本构模型进行驱动器设计,图2所示为驱动器简化模型。

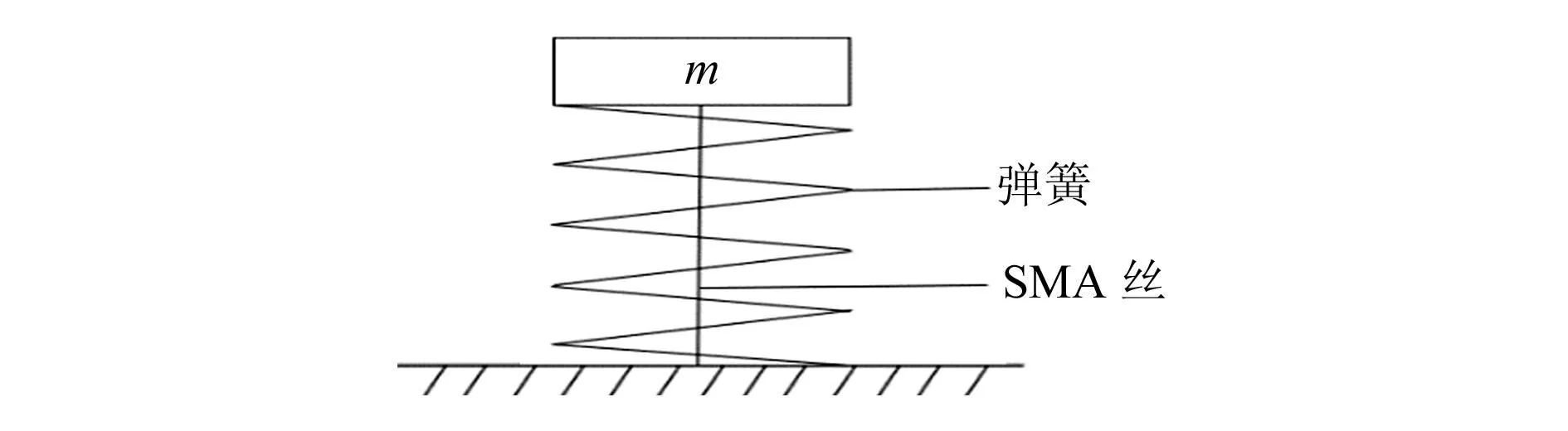
图2 驱动器模型简图

模型方程如下:

σ-σ0=Ω′(ξS-ξS0)+Θ′(T-T0)

(1)

其中:

(2)

式中:σ为应力,σ0为σ的初始值,ξS0为ξS的初始值,T为合金丝温度,T0为T的初始值,S为记忆合金丝的横截面积,D为弹性模量,L为合金丝的长度,k为弹簧刚度,Θ为热弹性系数,Ω为相变系数。

SMA在加热过程中应力与温度的关系如下:

(3)

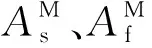
2.2 SMA丝材料本构参数标定

在进行本构方程拟合时,需要SMA丝材料参数。对本文装置所用的SMA丝进行DSC(差式扫描量热仪)测试以及室温和高温下的拉伸试验,实验仪器如图3所示,以获取其相变温度和马氏体与奥氏体相下的弹性模量。

何为翻译比喻？顾名思义，翻译比喻就是指把翻译活动或翻译活动中的主体——译者——比作其他事物。严格来说，翻译比喻只是一种感性的思考，比喻的创造者或使用者们借助于一些与翻译活动有着相似外形或者共同实质的事物来描述翻译，以突出翻译的特点。针对翻译比喻这一宽泛的概念，本文将探讨的范围局限在有关于译者的比喻，即专指译者或与译者有关的比喻，并非所有的翻译比喻。

图3 实验仪器

DSC实验仪器型号为梅特勒托利多DSCI,其升温速率为5 ℃/min,实验所得结果如图4所示。拉伸试验机型号为UTM4204-GD,室温和100 ℃下的拉伸实验结果如图5所示。

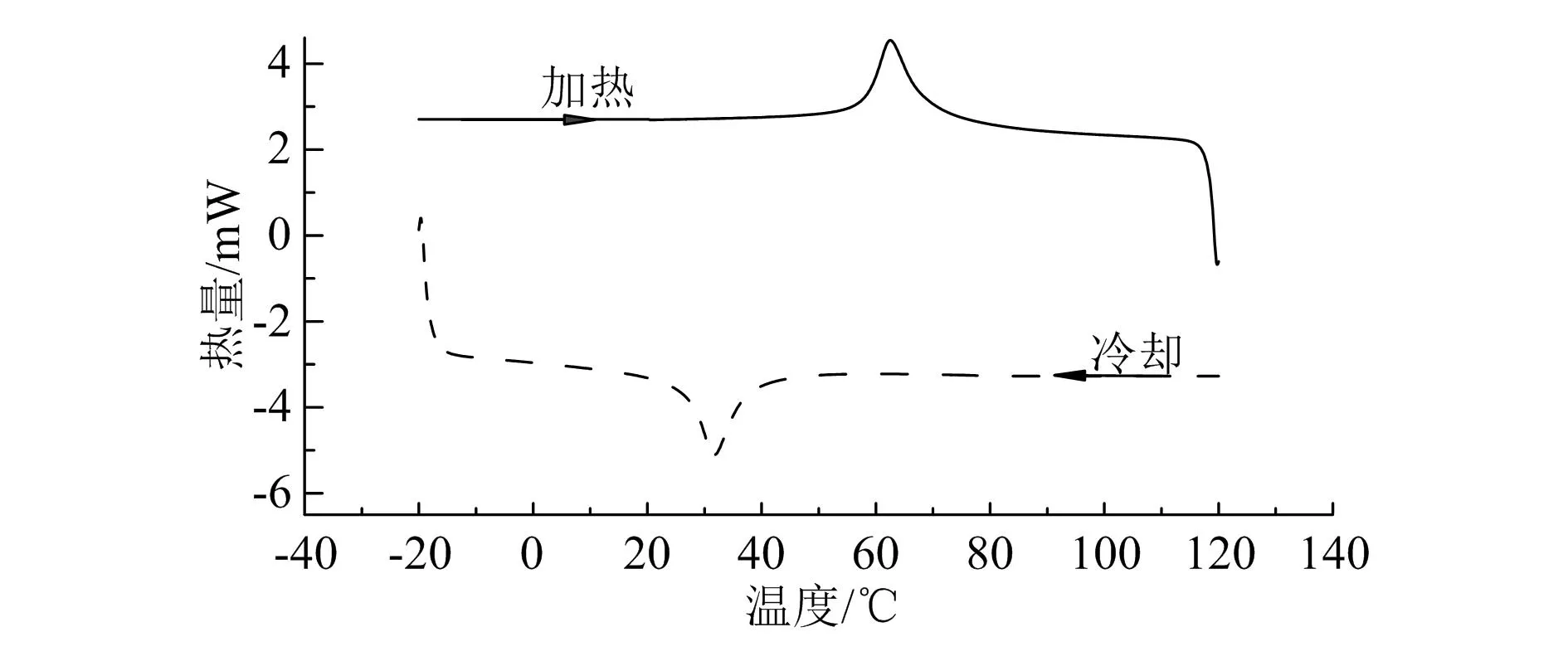
图4 样品DSC测试结果

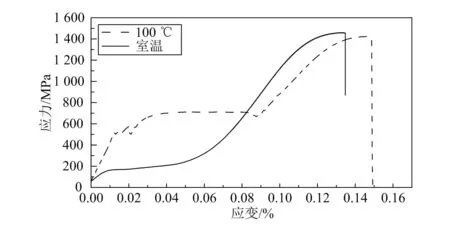
图5 室温和高温拉伸试验

实验所得SMA丝的部分参数见表1,表中Ms、Mf和As、Af分别为马氏体相变与奥氏体相变开始相变温度和结束相变温度,EA和EM为奥氏体和马氏体相时的弹性模量。

表1 SMA本构材料参数

2.3 驱动单元部件设计

为确定驱动器中驱动弹簧驱动力的大小,需要对分瓣螺母进行受力分析,如图6所示。

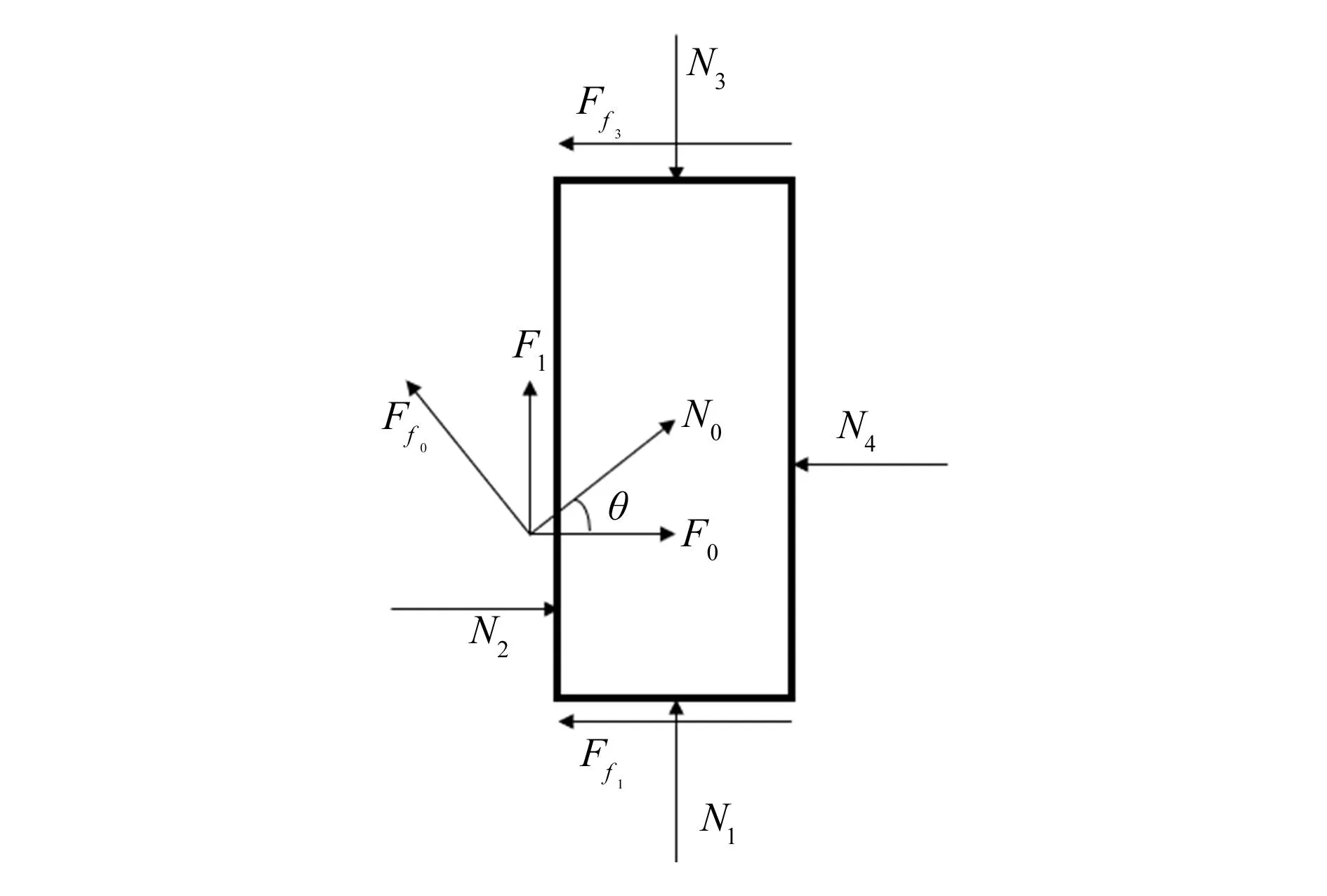
图6 分瓣螺母受力分析图

轴向力平衡方程:

N1+F1+Ff0·cosθ=N3

(4)

径向力平衡方程:

Ff0·sinθ+Ff1+N4+Ff3=F0+N2

(5)

其中:

F0=F1cotθ

(6)

Ff0=υ0N0

(7)

Ff1=υ1N1

(8)

Ff3=υ3N3

(9)

综合以上公式化简得到:

N4=F1(cotθ+tanθ)+N2

(10)

将轴向预紧力为5 kN、θ为60°代入式(4),得到钢球与分瓣螺母间的正压力为231 N,将该值的1.5倍作为驱动弹簧的初始设计参数之一。

根据装置安装条件,确定驱动弹簧中径D为36 mm,钢丝直径d为4 mm,材料为60Si2Mn,剪切模量G=8 000 MPa,取有效圈数为n=3,两端磨平。弹簧主要设计参数计算如下:

c=D/d

(11)

(12)

(13)

(14)

式中:c为绕旋;K为刚度系数;Fmax为最大工作载荷;τmax为最大剪切应力,为640 MPa;H0为自由高度;N为总圈数。由此,驱动弹簧设计参数见表2,表中H为弹簧初始安转高度。

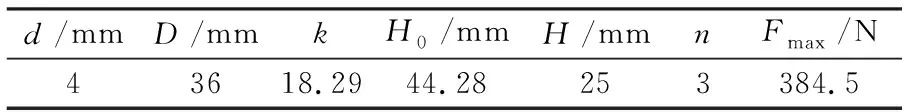
表2 驱动弹簧设计参数

同理,得到安全弹簧的设计参数见表3,弹簧材料为60Si2Mn。

表3 安全弹簧设计参数

2.4 分瓣螺母径向撑开机构设计

为了说明涡卷弹簧分离装置的优势,对传统的分离弹簧斜面径向撑开方式与本文的涡卷弹簧径向撑开方式进行比较。分离弹簧斜面径向撑开方式的斜面如图7所示。

图7 斜面示意图

根据高滨等[8]的研究,为了避免施加轴向推力时分瓣螺母和斜面发生自锁,其上、下端的接触角度必须满足:

(15)

式中:α和β为斜面与水平面的夹角,μ为摩擦系数。

对分离弹簧斜面径向撑开方式分析得知,当μ取0.2时,(α+β)必须大于22.6°。取α=β=11.3°,连接分离装置的分瓣螺母壁厚为2 mm,即z×cosα=2,其中z为斜面长度,分瓣螺母的径向位移为2 mm;径向所需推力为10 N,需要施加10.2 N的力;斜面位移为2.04 mm,总接触面积为109 mm2。在不考虑自身重力的情况下,斜面式分离方式弹簧推力在斜面上的分力会压紧斜面,从而产生大小为0.4 N的摩擦力,导致摩擦热的产生。该撑开方式因分离弹簧的存在,所需的轴向安装空间较大。因此,基于应用空间考虑,本文选择涡卷弹簧径向撑开方式。

对涡卷弹簧径向撑开方式进行分析,首先对平面涡卷弹簧进行受力分析,得到如下平衡方程:

F·l+ε=M·θ

(16)

式中:F为撑开手推力;l为推动距离,即分瓣螺母的径向移动量,取值为1.66 mm;γ为轴转过的角度,取γ=π;ε为撑开手与盘之间的摩擦热,由于本文设计的解锁装置解锁时间很短,因此可忽略摩擦热的影响。涡卷弹簧依据GB/T 7336—1994标准进行设计计算,具体设计参数见表4,弹簧材料为60Si2Mn。

表4 涡卷弹簧设计参数

3 分瓣螺母承载能力校核及装置预应力模态分析

3.1 分瓣螺母连接强度校核

分瓣螺母是解锁装置的主要承载部位,受预紧力和外部载荷作用,因此要对其进行强度校核,螺栓、分瓣螺母材料为双线性钢材,材料参数见表5。

表5 螺栓螺母材料参数

目前,很少对精细螺纹强度进行校核,因为对螺纹进行网格划分和有限元计算都比较费时费力。ANSYS软件中提供了螺栓预紧力,利用简化模型就能计算螺杆螺母真实的受力情况,本文在给定的预紧力下对螺纹连接强度进行校核,结果如图8～10所示。

图8 螺栓连接面应力分布

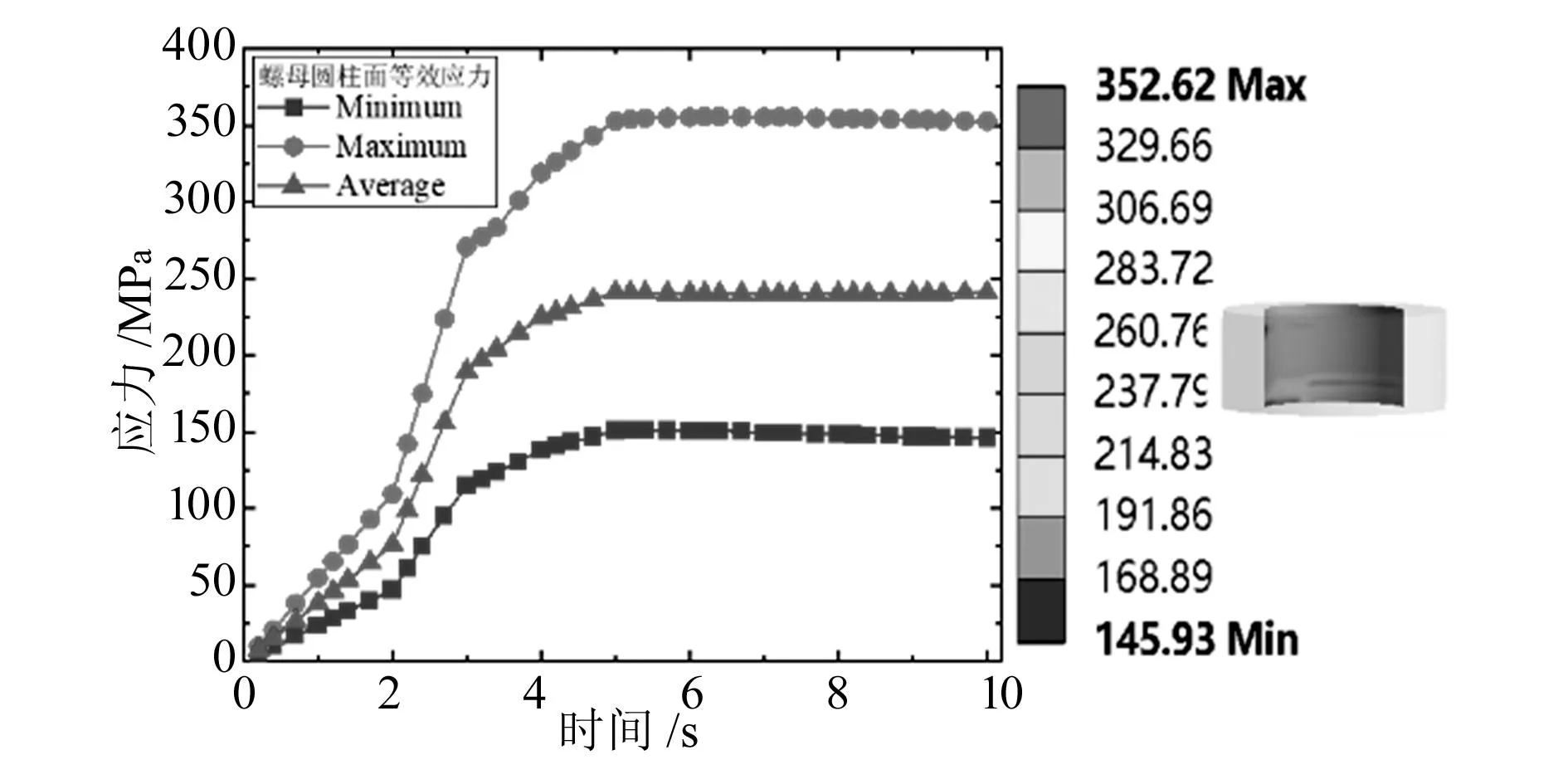
图9 螺母连接面应力分布

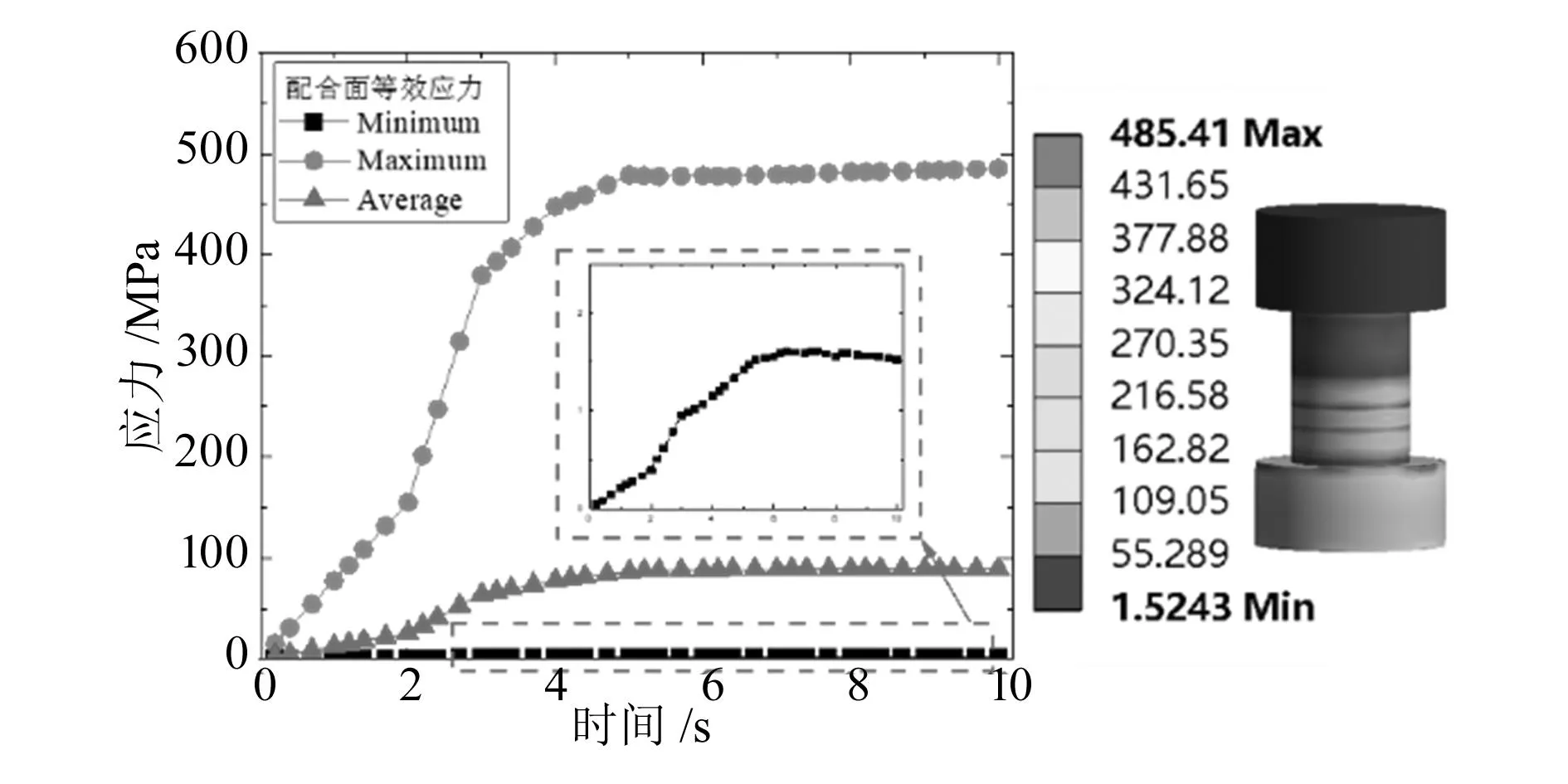
图10 螺栓连接整体应力分布

由仿真结果可知,螺栓圆柱面最大应力为330.87 MPa,螺纹圆柱面最大应力为352.62 MPa,均小于材料的屈服强度450 MPa,构件只发生弹性变形。而螺栓和螺母整体的应力为485.41 MPa,稍大于材料的屈服应力,但值得注意的是,应力最大的地方均在螺母的圆周,一般工程上都会对螺母进行倒角处理,因此可以减小此处的应力。综上所述,螺栓和螺母的强度满足连接要求.

3.2 装置预应力模态分析

为避免装置在工作时由于外界振动导致误解锁,需在预紧力条件下对其进行模态分析,即预应力模态分析[9]。将5 kN轴向预紧力施加在螺栓上,模态分析结果如图11、12所示。

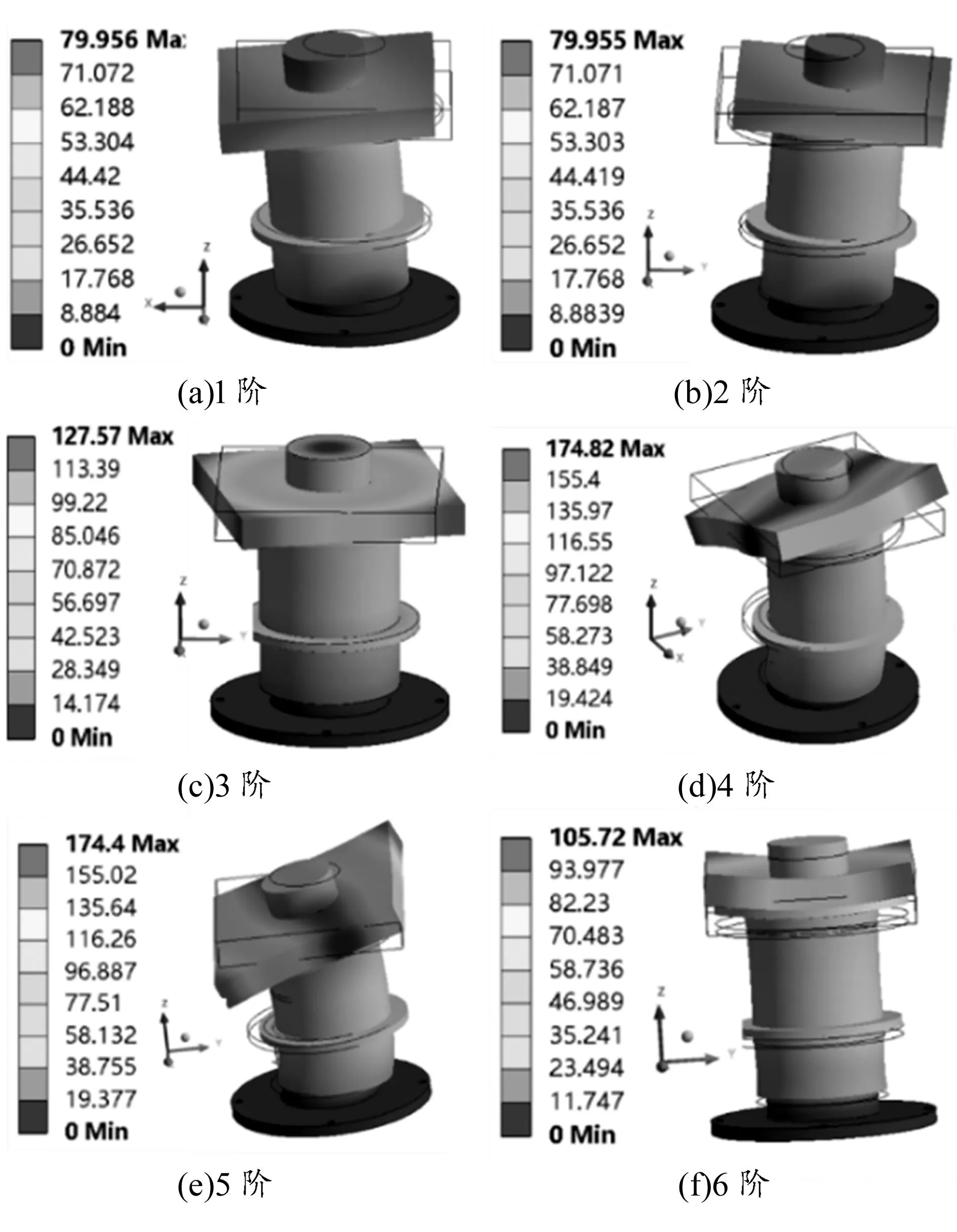
图11 各阶振型云图

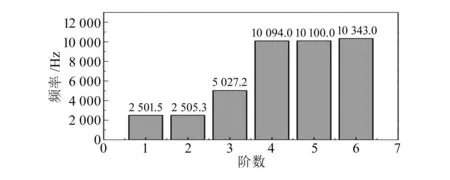
图12 各阶自振频率

1阶振型对应x方向的左右摆动,2阶振型对应y方向的前后摆动,3阶振型对应绕z轴的扭转,4阶振型对应绕y轴的扭转,5阶振型对应绕x轴的扭转,6阶振型对应z方向的上下窜动。通过对装置工作原理分析可知,出现误解锁最大的可能为装置z方向发生滑移。装置的6阶振型刚好对应z方向的上下窜动,但6阶振型的自振频率为10 343 Hz,而正弦振动的频率一般不会超过100 Hz,随机振动的频率也不会超过2 000 Hz[10],由此可见,该装置不存在由随机振动引起的误解锁风险。

4 结束语

本文对SMA丝驱动的直推式分瓣螺母解锁装置进行了设计与分析,得到了连接解锁机构驱动器的数学模型,并通过受力分析对系统各部件进行了计算,得到了具体设计参数。利用DSC实验和室温及100 ℃下的拉伸试验,对驱动器所用的记忆合金丝的本构参数进行了标定。在ANSYS中对分瓣螺母进行了静强度校核以及预应力模态分析,结果表明装置在工作条件下不会发生塑性变形,在随机载荷振动下也不会发生误解锁。