基于滑模理论的城市轨道车辆稳定性自动化控制研究
2024-03-11王天予周大琼梁修书
王天予,唐 平,周大琼,梁修书
(1.重庆交通大学交通运输学院,重庆 402260)
(2.重庆文理学院数学与大数据学院,重庆 402160)
(3.重庆城市职业学院,重庆 402160)
(4.重庆市江津区教师发展中心,重庆 402260)
常规的磁悬浮系统中存在无法确定具体参数、非线性以及不稳定开环等特征,如何更好地进行悬浮控制一直是业内研究的热点问题。20世纪90年代,龙志强等[1]进行了非线性补偿以及PI控制的设计,汪科任等[2]针对悬浮稳定性设计了以增益矩阵为基础的悬浮矩阵,然而以上技术没有解决多电磁铁时对应的误差协同及补偿。针对多电磁铁悬浮系统,本文以滑模理论为依据设计了磁悬浮系统的动力学模型,加入扰动观测器以及协同控制律,增强了磁悬浮车辆悬浮控制的稳定性,经过实验验证,该方法有效可行。
1 磁悬浮系统
1.1 系统简介
以磁悬浮列车单节车厢为例,磁悬浮系统构造如图1所示,系统包括5组磁悬浮架,用来支撑和保证车体悬浮稳定[3],磁悬浮架主要由极板、电磁铁模块、托臂、防滚吊杆以及防滚梁等组成。
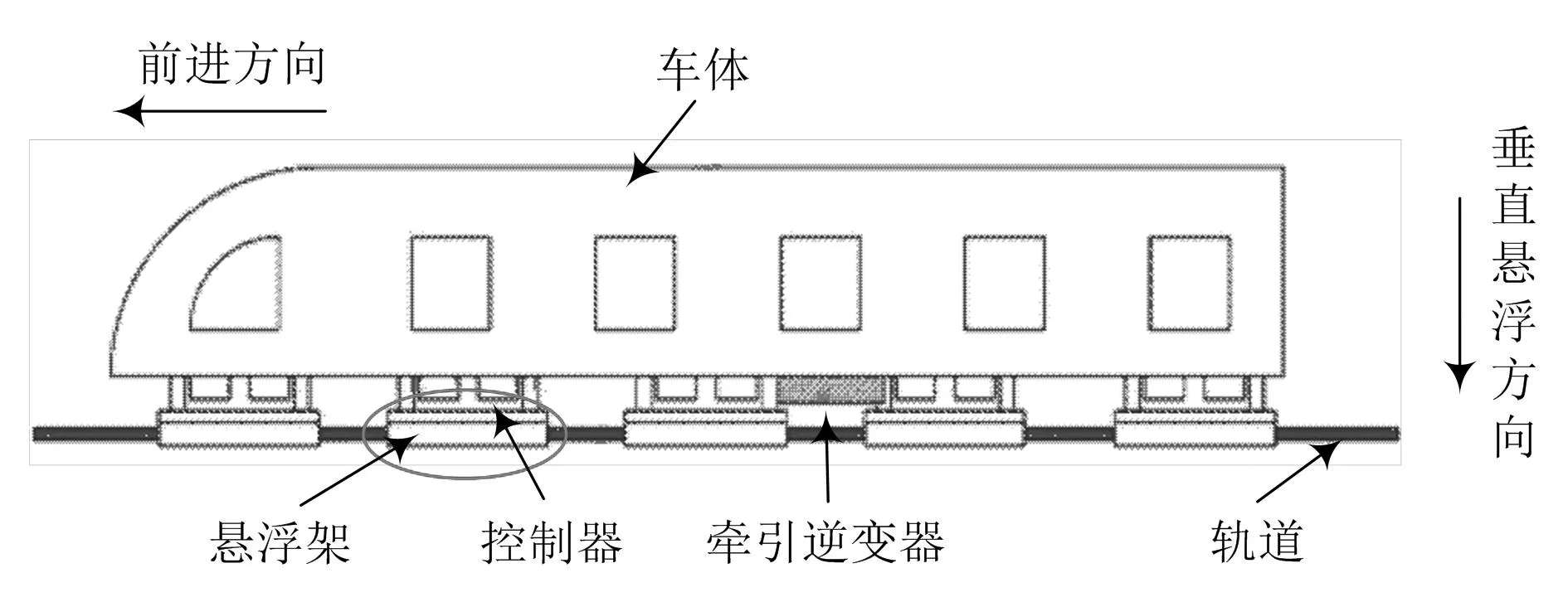
图1 磁悬浮系统示意图
1.2 系统动力学建模及分析
对磁悬浮系统进行动力学建模,所建动力学模型如图2所示。图中,电磁铁悬浮模块1由电磁铁线圈1、2组成,电磁铁悬浮模块2由电磁铁线圈3、4组成。电磁铁悬浮模块1、2的电磁力分别为Fm1与Fm2,电磁铁悬浮模块1、2与轨道之间的悬浮间隙分别为τm1与τm2,O为质心,模块中心到O的距离为a,刚性极板相对于水平面的倾角为α。

图2 系统动力学模型
设4个电磁铁线圈有相同的匝数Nm,则基于图2所示的动力学模型[4]并结合电磁学理论[5],可以将磁悬浮系统电磁力描述为:
(1)
式中:μ0为空气磁导率,S为磁极面积,im1、im2分别为电磁铁悬浮模块1、2的控制电流,t为时间。
由于极板的倾角很小,且电磁铁悬浮模块与轨道间的悬浮间隙也很小,因此结合图2及式(1)可以将极板的倾角α近似为:
(2)
中心点竖直方向对应的位移分量τg为:
(3)
极板旋转引起的位移τα为:
(4)
极板质量对模型影响较小,可以忽略不计,则模型在竖直方向上受到的合力Fg为:
Fg=Fm1+Fm2-2msg
(5)
式中:电磁铁悬浮模块1及2的质量均为ms,g为重力加速度。
极板与质心产生的转矩Tα为:
Tα=-(Fm1-Fm2)a
(6)
质心的动力学方程如下:
(7)
(8)

设mα=I/a2,mα为极板旋转的等效转动质量,结合式(6)及式(8)可以得到:
(9)
式中:Fα为导致极板旋转的合力。将公式(7)代入式(9),合并同类项可以得到:
(10)

2 滑模控制器设计
2.1 扰动观测器设计
为了更好地量化干扰量,需要设计扰动观测器[6-7]。建立一数学模型,该模型可以在控制器中更好地处理干扰量对磁悬浮控制的影响。假设干扰项Wi(t)和未建模时的动态非线性特性ΔDmi及气动阻力ΔBmi以及它们的导数是已知的有界函数,设定观测误差分别为:
(11)

(12)
其中:
(13)

2.2 滑模控制律设计
加入扰动观测器以及斩波器[8]的滑模控制系统如图3所示。
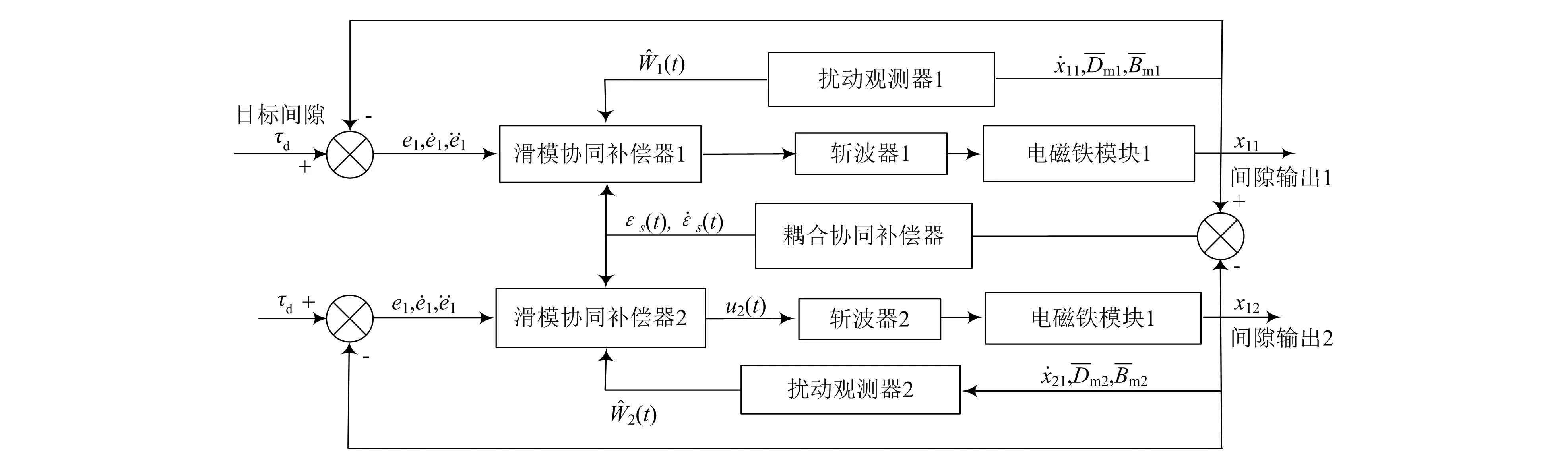
图3 滑膜控制系统
模型跟踪误差ei(t)为:
ei(t)=xi1(t)-xd
(14)
式中:xd为期望输出。
式(14)对时间求导得到磁悬浮架的速度和加速度:
(15)

(16)

结合图3,可以将滑模协同控制律μi(t)设定为:
μi(t)=μieq(t)+μisw(t)+μioh(t)
(17)
式中:μisw(t)、μieq(t)分别为第i个电磁铁模块中的切换控制律和等效控制律[11],μioh(t)为耦合协同时对应的补偿项。
基于扰动观测器预估值,等效控制律可以表述为:
(18)
切换控制律可以表述为:
(19)
式中:ξ1、ξ2为切换系数。切换控制律能够使模型到达滑模面的状态,但采用sgn()函数无法保证引入的控制量具有连续性,容易出现振颤现象[12],因此使用饱和函数sat()函数等效sgn():
(20)
式中:φ0为边界层厚度。由于采用了饱和函数,因此能够保证控制量的连续性。
耦合协同时对应的补偿项为:
(21)
由式(21)可以看出,补偿项受电磁铁模块同步误差及交叉耦合系数的影响,当系数c1、c2均为0时,将不能实现控制协同的功能,不能够补偿间隙产生的同步误差。
3 实验与结果分析
3.1 实验设计
通过设计磁悬浮系统实验平台对协同控制效果的有效性进行实验验证。搭建的平台如图4所示,包括电磁铁模块2组、磁悬浮控制器2套、磁悬浮传感器2个。磁悬浮控制器的通信以及耦合通过CAN总线连接实现,电磁铁控制模块示意图如图5所示。

图4 磁悬浮系统实验平台
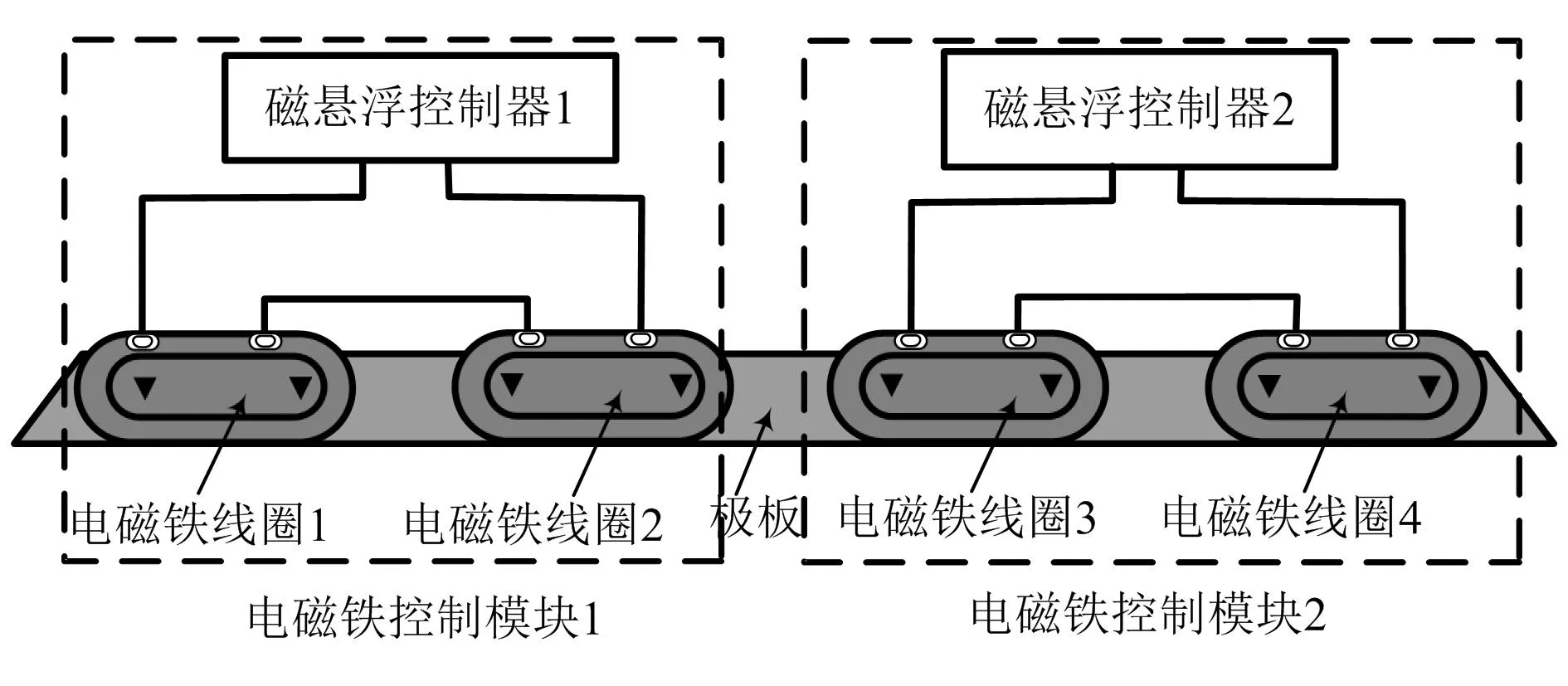
图5 电磁铁控制模块示意图
实验分两组进行,通过对比两组实验结果进行验证。一组实验使用传统PID控制,不加入协同控制,PID的比例增益Kp的值设为9 500,积分增益Ki的值设为100,微分增益Kd的值设为370;另一组实验使用基于滑模理论的控制系统,系统参数见表1。
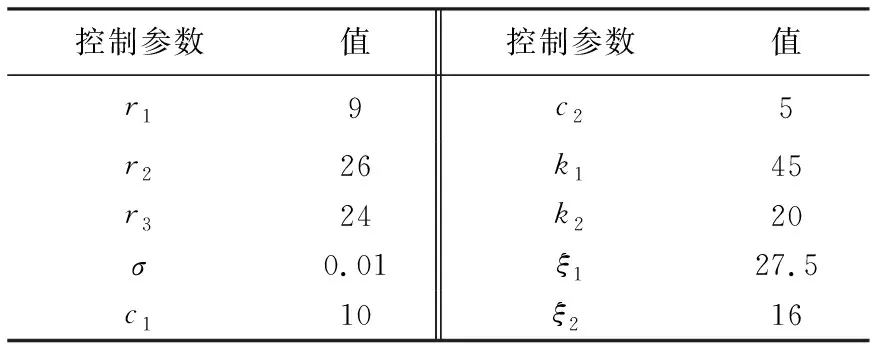
表1 基于滑模理论的控制系统参数
3.2 结果分析
第一组实验仅通过PID控制进行系统控制,设计工况为空气弹簧均不进行充气,当磁悬浮架稳定在静态悬浮状态时,在平台上方1 m的位置间隔7 s先后施加100 N的载荷,冲击力实验中数据采样的频率为512 Hz。磁悬浮模块的悬浮间隙变化如图6所示,悬浮电流波动如图7所示。

图6 PID控制悬浮间隙
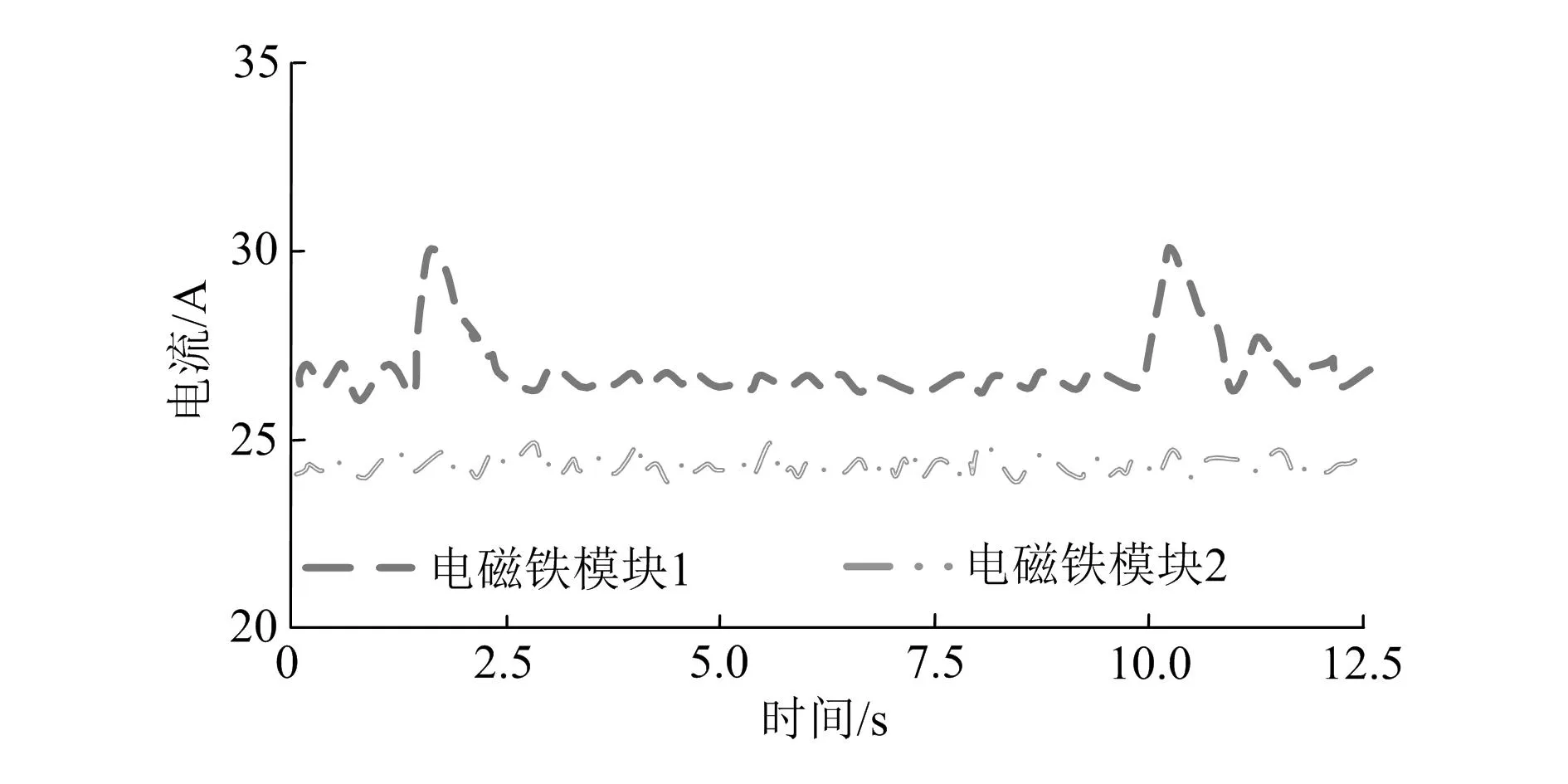
图7 PID控制悬浮电流
由图可知,仅为PID控制时,两次载荷冲击下电磁铁模块1悬浮间隙波动幅值最大为0.430 mm,电磁铁模块2悬浮间隙波动幅值最大为0.030mm。电磁铁模块1的电流波动幅值最大为4.7 A,电磁铁模块2电流波动幅值较小,在1.0 A左右。
第二组实验工况、条件与第一组相同,控制系统采用以滑模理论为基础、加入协同控制律的控制系统,得到的悬浮间隙变化如图8所示,悬浮电流波动如图9所示。

图8 改进控制系统悬浮间隙
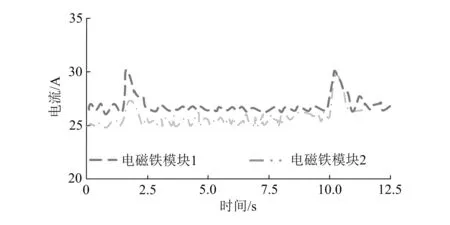
图9 改进控制系统悬浮电流
由图可知,两次载荷冲击下电磁铁模块1悬浮间隙波动幅值最大为0.262 mm,电磁铁模块2波动幅值最大为0.249 mm。电磁铁模块1悬浮电流波动幅值最大为2.12 A,电磁铁模块2悬浮电流波动幅值最大为2.21 A。
综合图6~图9可知,单纯使用PID控制系统,电磁铁模块1与电磁铁模块2的悬浮间隙差值较大,最大为0.400 mm,电流波动差值最大达到3.7 A;使用基于滑模理论的控制系统时,由于加入了协同控制律,悬浮间隙差值最大仅为0.013 mm,电流波动值最大仅为0.09 A。由此可以看出,改进控制系统能够更好地降低悬浮间隙差值,与单纯PID控制相比,跟踪误差约减少了40%,在更大程度上避免了滑橇触轨。
4 结束语
本文针对磁悬浮车辆悬浮控制问题,提出了基于滑模理论和协同控制律的控制系统。实验结果表明,该系统能更好地避免电磁铁的耦合扰动,提高车辆稳定性。与传统的PID控制相比,基于滑模理论的控制具有更好的鲁棒性和适应性,但仍有优化空间,如优化扰动观测器性能、实现更好的协同控制等。未来,将继续关注磁悬浮车辆的研究动态,以期取得更多创新成果。
