基于VARTM的碳纤维单向与三维编织混杂织物树脂灌注工艺

2024-03-11户迎灿张联合崔健谢金路王晓明任浩张健榜查一斌秦成张辉倪宇峰

工程塑料应用 2024年2期

户迎灿，张联合，崔健，谢金路，王晓明，任浩，张健榜，查一斌，秦成，张辉，倪宇峰

(1.中车青岛四方机车车辆股份有限公司，山东青岛 266111；2.东华大学材料科学与工程学院纤维材料改性国家重点实验室，上海 201620； 3.东华大学机械工程学院，上海 201620)

碳纤维增强树脂基复合材料(CFRP)凭借比强度和比模量高、耐疲劳性好、可设计性强等优势，在地铁列车减重提速方面效果显著。转向架作为地铁关键承力结构之一，主要用以控制、平衡轨道上的总质量，同时减少轨道磨损，但传统钢质转向架约占列车总重的37%[1]，采用CFRP对其结构进行轻量化设计，不仅可以有效减轻列车的结构质量，还可以显著提高车辆的安全性能和使用寿命。

对于地铁转向架侧梁这类大型复杂形状结的构件，需要对局部典型结构件进行试制并对树脂灌注过程进行分析。以往在试制过程中通常采用人工试错法，不仅效率较低，而且造成了生产成本的增加。数值模拟的快速发展，逐渐成为对大型复杂结构件试制的主要研究手段，不仅可以对各种制件进行树脂灌注模拟，对过程进行可视化，还可以为实际生产加工提供一定的指导[2]。

20世纪90年代，已经研究并开发了树脂传递模塑(RTM)成型工艺树脂灌注过程的模拟技术[3-4]。其中包括具有规则边界的二维几何体的有限差分法、考虑瞬态效应的有限元技术和有限元/控制体技术。有限元/控制体一致性技术使用有限元方法求解压力场的控制方程，并使用控制体积方案跟踪树脂流动前沿的位置，研究表明，采用有限元/控制体技术非常适合树脂灌注充模时的数值模拟，目前已被确立为RTM充模模拟商业软件的标准[5-6]。

Kim等[7]提出了一种预测剪切变形机织物渗透性的解析模型，利用PAM-FORM和PAM-RTM软件对U型复合材料结构的真空辅助树脂传递模塑(VARTM)成型过程进行了仿真，发现模拟与实验制备的树脂填充时间和流动前沿较为匹配。Rodrigues等[8]利用PAM-RTM软件研究不同注射压力下CaCO3的加入对树脂浸润纤维预制体的影响，结果表明树脂流动前沿、充填时间、充填压力等参数数值计算结果与实验数据吻合良好。高猛等[9]通过PAM-RTM软件对复合材料电池箱上盖板的RTM树脂充填过程进行模拟，发现树脂充模时间与树脂黏度、纤维体积含量、压缩速度相关。Grössing等[10]的研究表明PAM-RTM软件可用于预测树脂灌注过程中流动前沿随时间变化趋势以及结构件内部的干区气泡等缺陷。

三维编织碳纤维织物内部呈相互交织的空间网状结构，具备优异的吸能特性。但受到编织角大小和轴向纱线数量的限制，复合材料轴向性能较低，无法满足一些对轴向承载性要求较高的复合材料结构件的应用要求。而单向碳纤维具备优异的轴向性能，将三维编织与单向碳纤维混杂增强不仅可以实现优势互补，还可以减少织物不同渗透率对复合材料灌注成型过程的影响。因此，为验证单向和三维编织混杂织物增强环氧树脂复合材料的成型工艺性，分析树脂的流动规律，基于以上研究，笔者对侧梁典型结构复合材料方形管进行缩比建模，利用PAM-RTM软件对方管进行树脂灌注模拟并与VARTM工艺制备的方管进行对比分析。

VARTM是RTM的衍生工艺，采用单侧模具的形式，可以降低模具的使用成本，其主要流程为：先将碳纤维增强材料在底部模具中铺设，然后在真空袋下覆盖和密封，空气从空腔中抽出，依靠大气压力将树脂注入碳纤维增强材料。

采用VARTM工艺制备得到的单向和三维编织混杂织物复合材料方管，其产品质量主要取决于树脂对单向和三维编织混杂增强织物的浸润程度，而且单向织物和三维编织织物的结构不同，导致树脂对两种织物的浸润性不尽相同。采用数值模拟的方法可以将VARTM中的树脂灌注过程可视化，通过建立不同的模型还可以观察到每层铺层树脂的浸润程度，预测整个VARTM中树脂灌注过程的灌注时间以及灌注质量[11]。

1 实验部分

1.1 主要原材料

单向碳纤维织物：T700，300 g/m2，宜兴市中碳科技有限公司；

三维编织碳纤维织物：T700，1 200 g/m2，采用352锭环形编织机制备的三维角联锁结构编织织物，编织角为30°，厚度为1.33 mm，江苏高路复合材料有限公司；

环氧树脂：ME306R-A[12]，东华大学；

固化剂：ME306R-B[12]，东华大学；

丙酮：WF300，上海凌峰化学试剂有限公司；

柔性真空袋薄膜：LVF2308，上海沥高科技股份有限公司；

导流网：VI130W，上海沥高科技股份有限公司；

聚四氟乙烯管：DG-SF12，上海道冠橡塑五金有限公司；

脱模布：R60AD，上海沥高科技股份有限公司；

脱模剂：Zyvax®Flex-ZTM 5.0，肯天化工(上海)有限公司；

密封胶带：AT-200Y，上海道冠橡塑五金有限公司。

1.2 主要仪器及设备

真空泵：WOB-L，上海泰坦科技有限公司；

树脂收集器：RB10-1214，厦门宥德材料科技有限公司；

玻璃板：1 000 mm×600 mm×8 mm，滕州市优瑞商贸有限公司；

大型工业烘箱：YB-1，上海亦博实业有限公司；

分析天平：HZT-A，苏州金钻称重设备有限公司；

游标卡尺：DL3944，宁波得力集团有限公司。

1.3 碳纤维增强织物面内渗透率的理论模型

VARTM工艺树脂灌注过程中，碳纤维织物的渗透率是极为关键的参数。渗透率作为纤维织物的固有属性，反应的是纤维织物对树脂流动的阻碍作用，对树脂的灌注过程有着直接的影响，直接决定了数值模拟的准确性，包括预测树脂流动前沿的位置、灌注所需时间以及气泡和干斑等缺陷的产生。

碳纤维织物的渗透性通常由纤维束和纤维束间隙的特性决定，即取决于多孔结构的几何形状，与流体性质和流动机制无关[13]。对于较薄的纤维织物，可以假设两个主轴位于织物平面内，第3个主轴的方向与织物平面垂直[14]。目前，已有大量关于具有特定结构纤维织物渗透性的建模工作，特别是解决几何结构高度形成的双尺度孔隙的问题[15-16]。

然而，采用建模方式难以准确量化不均匀分布的纤维丝束的渗透性以及束间间隙的几何形状对纤维织物渗透率的影响。因此，描述纤维织物渗透率的模型通常对纤维体积分数具有一定依赖性，这在很多实际应用中得到了验证，但同样不能准确预测具有复杂孔隙网络纤维织物的渗透率。所以目前只能通过实验的方式对织物渗透率进行测定，或在数值模拟中详细设定可以描述增强织物孔隙形状和尺寸的参数，通过数值模拟的方法进行模拟实验[17]。

树脂浸润织物的过程属于非饱和径向流动，受到拉普拉斯方程控制，其由达西定律和不可压缩流体的连续方程组合而成，达西定律[18]基本表达式见式(1)。

式中：v是树脂流动的速度；ΔP是施加的压力梯度；μ是树脂的黏度；K是渗透率张量。

Weitzenböck等[19]为了计算各向同性增强织物渗透率，将模具内的压力梯度确定为流动前沿位置的函数，通过极坐标系下求解拉普拉斯方程进行实现，将新的压力分布带入达西方程，利用边界条件获得了各向同性增强织物的理论计算模型公式，见式(2)。

式中：rf是实际流动前沿半径；r0是注胶口半径；t，ε分别是时间和孔隙率。

对于各向异性纤维织物，在树脂流动过程中可以观察到椭圆形流动前沿，因此压力分布的二阶偏微分方程不再是拉普拉斯方程[19]，见式(3)。

通过应用物理域变化可以将各向异性系统转换成准各向同性进行求解或者利用笛卡尔坐标系转换成极坐标系进行求解。Khan等[20]对二维径向流的数学模型进行求解，使用了Ahn等[21]提出的二维径向流法确定的平面内渗透率的公式，见式(4)和式(5)，不同的数学模型或者转换方式以及求解过程的假设条件不一样都可能得到不同的解析解。

式中：x0和y0是按比例缩放的入口尺寸；xf和yf是实际流动前沿的半长轴和半短轴的尺寸；tf是当前流动前沿的时间；φ为织物孔隙率。

本次实验测定主要考察树脂在面内两个方向上的树脂流动情况，采用了基于达西定律二维渗透率表达式，见式(6)。

式中，ux是x方向树脂充模速率；uy是y方向树脂充模速率是二阶渗透率张量；η为黏度。

不可压缩流体运动的连续方程见式(7)。

将式(6)代入式(7)可以得到式(8)。

由于二维渗透率张量是对称张量，即Kxx=Kyy，公式(8)可以简化为式(9)。

由于PAM-RTM软件可以定义渗透率方向，因此在测试碳纤维织物渗透率的过程中，可以直接测定主/辅渗透率方向上的渗透率，无须考虑渗透率主/辅方向是否与碳纤维织物的横向和纵向方向一致，主/辅渗透率方向渗透率具有正交各向异性，所以增强织物的充模前锋会近似椭圆形，则渗透率张量可以表达为：

则式(10)变为：

将式(11)进行极坐标转换可以得到(下标e表示极坐标转换)：

测定条件是在恒定注射压力下进行，可定义边界条件为：注入口r=r0处，P=Pin(注胶口处压力)；流动前沿r=rie处[rie是i方向上t时刻树脂充模前锋位置，i=(x,y)]，P=Pf(流动前沿处的压力)，求解式(12)得到式(13)：

根据多孔介质孔隙中实际流体流动速率与平均流速的关系，可得式(14)：

对式(14)求积分得到树脂充模前锋位置与时间t的关系，见式(15)。

即可得到渗透率的计算公式，见式(16)和式(17)。

式中：rxe是主渗透率方向上t时刻树脂充模前锋位置；rye是辅渗透率方向上t时刻树脂充模前锋位置。

1.4 碳纤维增强织物面内渗透率的测定

渗透率主要取决于纤维结构，与流体性质和流动机制无关，因此可以选取替代测试液进行测定，但要满足牛顿流体和不可压缩的性质，本次渗透率测定采用二甲基硅油代替树脂，采用实验室自制的试验装置，如图1所示。

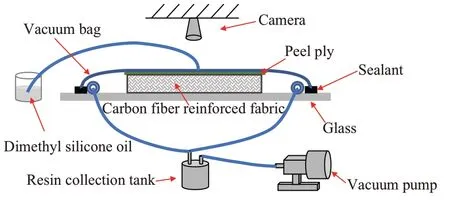
图1 增强织物渗透率测定试验装置示意图Fig. 1 Schematic diagram of the test device for determination of permeability of reinforced fabrics

首先，将单向织物裁剪成360 mm×200 mm的尺寸备用。之后用干净的医用纱布蘸取丙酮擦拭玻璃板模具并晾干，在玻璃板模具上用密封胶带围成比增强织物尺寸大50 mm的矩形区域，依次铺设单向织物和脱模布，完成后用打孔器在真空袋中间打孔，将孔定位在单向织物中间位置并把真空袋沿着密封胶带进行密封。随后连接好注胶和出胶管道以及阀门，关闭注胶阀门，打开出胶阀门和真空泵进行抽真空，真空泵压力为0.1 MPa，保压12 h并且压力始终保持不变后，将刻度尺沿主/辅渗透率方向固定。最后启动摄像机并同时打开注胶阀门开始灌注，记录灌注全过程。对于三维编织织物渗透率测定，只需将单向织物渗透率测定中的单向织物替换成三维编织织物，两种增强织物渗透率测定如图2所示。

图2 增强织物渗透率测定Fig. 2 Permeability determination of reinforced fabrics

增强织物的渗透率可以通过树脂流动前锋的位置进行计算，并且对树脂流动前锋的位置处理后得到新的树脂充模前锋位置Ti，可以发现Ti和渗透率之间存在线性关系，因此，可以通过线性拟合的方式对试验测定的数据进行拟合操作。令：

式中，Ti是将原t时刻树脂流动前锋半长轴和半短轴处理后得到新的t时刻树脂充模前锋位置，其中i=(x，y)。

2 结果与讨论

2.1 碳纤维增强织物面内渗透率测定结果

2.1.1 单向碳纤维织物面内渗透率测定结果

通过摄像机记录单向织物渗透率(KU)测定过程中的树脂流动前锋位置，每隔5 s采集一次主/辅渗透率方向t时刻树脂流动前锋位置，由于初始时刻二甲基硅油测试液流动前锋并不明显，因此从10 s开始记录t时刻树脂充模前锋位置，x方向树脂充模前锋记为rUxe，y方向树脂充模前锋记为rUye，具体结果见表1。

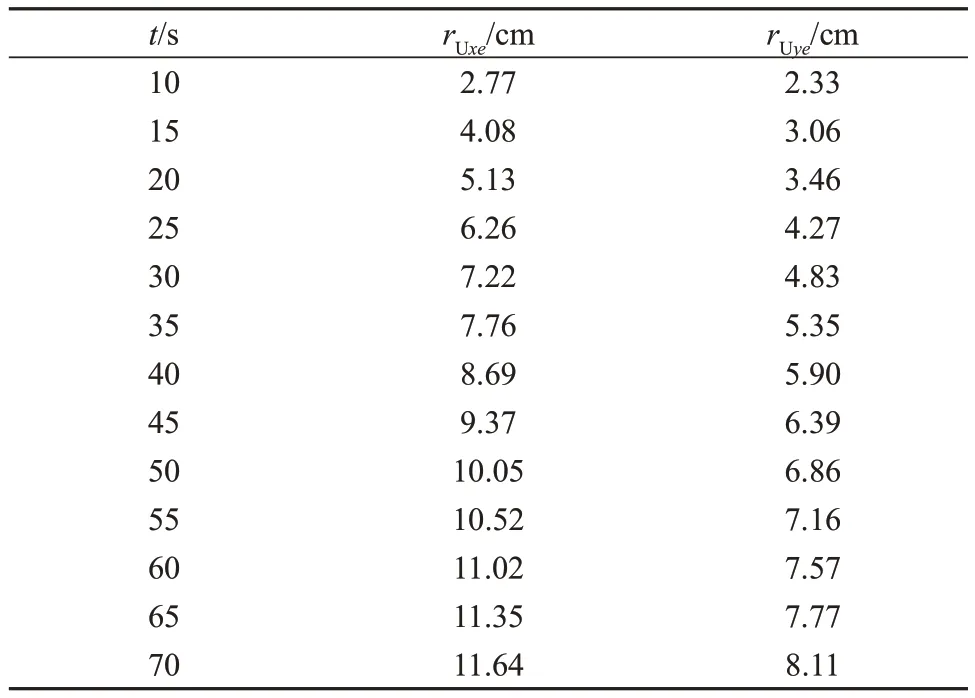
表1 单向织物主/辅渗透率方向t时刻树脂充模前锋位置Tab. 1 Resin filling front position at time t in the main/auxiliary permeability direction of unidirectional fabric

使用公式(18)对表1中单向织物主/辅渗透率方向t时刻rUxe和rUye处理，得到处理后t时刻树脂充模前锋位置TUx和TUy，并与灌注时间t进行线性拟合，结果如图3所示。R2代表试验数据与理论模型中拟合函数之间的吻合程度，R2越接近1，吻合程度越高。

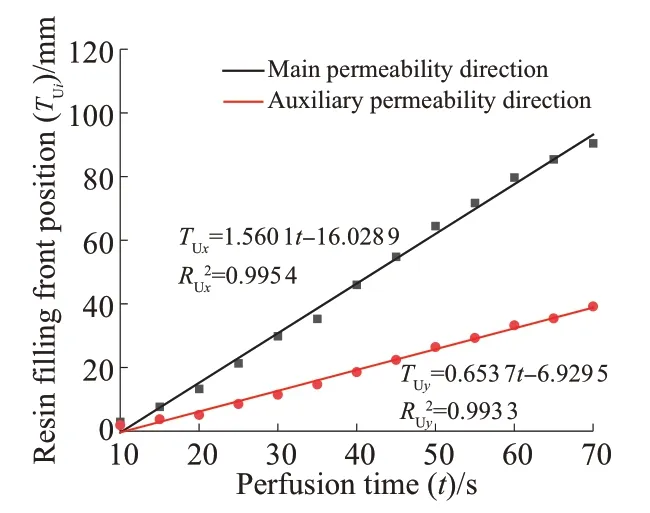
图3 单向织物主/辅渗透率方向树脂充模前锋位置拟合结果Fig. 3 Fitting results of resin filling front position in the main/auxiliary permeability direction of unidirectional fabric

图3结果表明，单向织物主渗透率(KUxx)拟合结果中RUx2为0.995 4，辅渗透率(KUyy)拟合结果中RUy2为0.993 3。随后将主/辅渗透率方向拟合斜率代入公式(16)和公式(17)中，计算得到KUxx=1.12×10-10m2，KUyy=4.70×10-11m2。

2.1.2 三维编织碳纤维织物面内渗透率测定结果

通过摄像机记录三维编织织物渗透率测定全过程中的树脂流动前锋位置，由于测定初始时刻树脂流动前锋并不明显，因此从12 s开始采集数据，此后每隔10 s记录一次主/辅渗透率方向树脂流动充模前锋位置，x方向记为rFxe，y方向记为rFye，数据见表2。

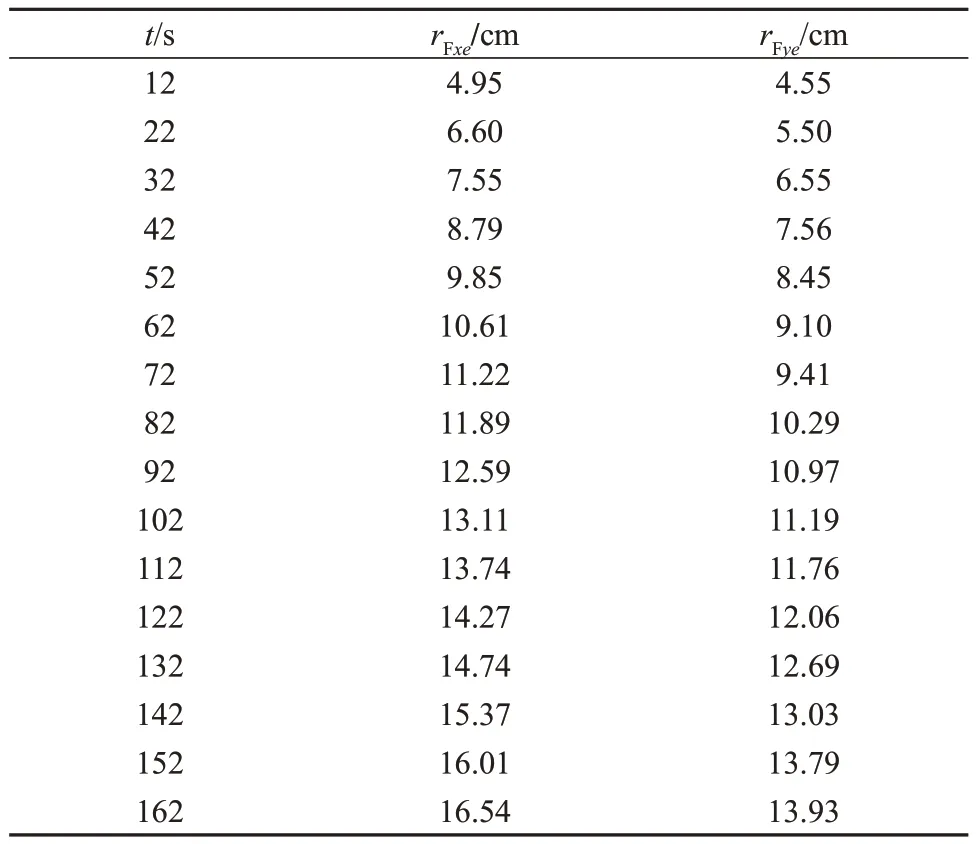
表2 三维编织织物主/辅渗透率方向t时刻树脂充模前锋位置Tab. 2 Resin filling front position at time t in the main/auxiliary permeability direction of three-dimensional woven fabric

通过公式(18)对三维编织织物t时刻rFxe和rFye进行处理，得到t时刻树脂充模前锋位置TFx和TFy，与时间t进行线性拟合，结果如图4所示。三维编织织物主渗透率(KFxx)树脂充模前锋位置的线性拟合结果中RFx2为0.998 1；辅渗透率(KFyy)树脂充模前锋位置的线性拟合结果中RFy2为0.996 7。将主/辅渗透率方向树脂流动前锋位置线性拟合的斜率代入公式(16)和公式(17)中，计算得到KFxx=8.03×10-11m2和KFyy=5.54×10-11m2。

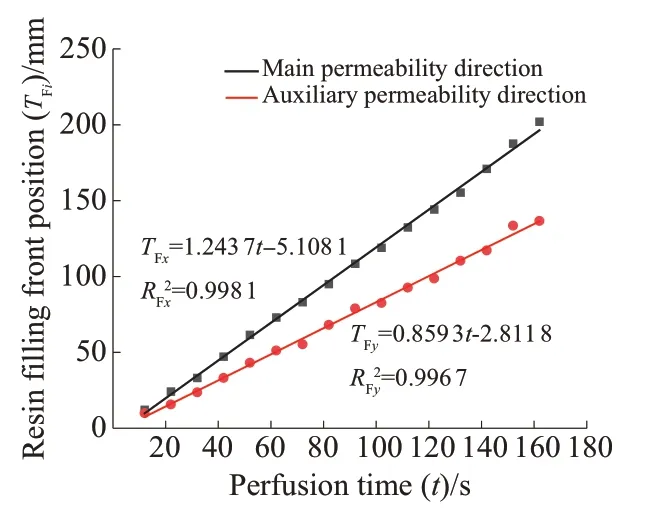
图4 三维编织织物主/辅渗透率方向树脂充模前锋位置拟合结果Fig. 4 Fitting results of resin filling front position in the main/auxiliary permeability direction of three-dimensional woven fabric

从以上数据可以看出，单向织物主渗透率(KUxx)最大，三维编织织物主/辅渗透率(KFxx，KFyy)次之，单向织物辅渗透率(KUyy)最小。这主要是因为单向织物沿主渗透率方向取向度高，孔隙结构较为简单，流体在单向织物主渗透率方向流动阻碍小，而三维编织织物内部纤维交织，取向均匀，主/辅渗透率值差异较小。

2.2 复合材料方管VARTM工艺树脂灌注过程的模拟分析

2.2.1 树脂灌注过程仿真模拟参数

在使用PAM-RTM软件对复合材料方管进行VARTM工艺树脂灌注过程仿真模拟时，根据实际工艺的工况条件，对仿真模拟参数进行合理预设。而仿真模拟参数中最重要的是碳纤维织物的渗透率以及灌注过程边界条件的设置，由于PAM-RTM软件的自身特点，可以根据碳纤维织物的主/辅渗透率和方向进行定义。仿真模拟过程采用恒压注射，具体参数见表3。

表3 仿真模拟相关参数Tab. 3 Simulation related parameters

2.2.2 树脂灌注过程仿真模拟

利用三维建模软件CATIA建立复合材料方管模型，然后将建立完成的方管模型导入HyperMesh软件中，对方管模型进行网格划分，针对PAM-RTM软件的特点，网格划分为三角形网格，网格尺寸选择5 mm，网格单元共10 096个；最后将方管模型导入到PAM-RTM软件中，进行仿真模拟基本参数的设置和边界条件设置，如图5所示，表面蓝色区域代表注胶口位置，即实际工况中的导流网区域，绿色区域代表出胶口位置。

图5 复合材料方管边界条件设置Fig. 5 Setting of boundary conditions for composite square tube

根据复合材料方管实际铺层要求，单向和三维编织织物交替铺层，对建立的模型进行区域划分，如图6所示，Zone1，Zone11，Zone21，Zone31，Zone41分别对应单向织物、三维编织织物、单向织物、三维编织织物和单向织物。

图6 复合材料方管铺层区域划分Fig. 6 Division of layered areas for composite square tube

将相关模拟参数以及注胶口和出胶口的位置设置完成后，运行PAM-RTM软件进行计算，得到复合材料方管填充时间分布结果和填充压力分布结果，分别如图7和图8所示。

图7 复合材料方管填充时间分布云图Fig. 7 Cloud map of filling time distribution for composite square tube

图8 复合材料方管填充压力分布云图Fig. 8 Cloud map of filling pressure distribution for composite square tube

针对图7复合材料方管填充时间分布结果进行分析，左侧图谱中不同颜色代表了不同的填充时间，从蓝色到红色，填充时间依次增加，同时也表示树脂浸润碳纤维增强织物的先后，填充时间分布结果显示填充时间为3 897 s。

在图8复合材料方管填充压力分布云图中，左侧图谱中不同颜色代表了不同位置的压力分布，从蓝色到红色，压力分布呈上升趋势，蓝色表示真空压力，红色表示注射压力。并且能够观察到，距离注胶口越近的区域压力越大，而距离出胶口越近的区域越接近真空压力。

2.3 复合材料方管的VARTM成型与分析

2.3.1 复合材料方管的VARTM成型工艺流程

使用VARTM工艺制备单向和三维编织混杂织物复合材料方管的主要流程如图9所示。

图9 VARTM成型工艺流程Fig. 9 VARTM forming process

(1)选取合适的硬质泡沫作为方管的模具，另一侧采用柔性真空带包覆，而且采用单侧模具可以降低生产成本。

(2)在硬质泡沫表面按单向/三维编织/单向/三维编织/单向的铺层设计进行铺层，铺层完成后再铺一层脱模布，方便后续脱模，并在其中一个端口脱模布表面铺导流介质，加快树脂的流动，减少树脂灌注时间。

(3)在铺有导流介质的一侧接注胶口，另一侧接出胶口，利用柔性真空袋将整套装置密封，并在出胶口管道处依次连接树脂收集器和真空泵。

(4)检查装置的气密性，若气密性良好，方可进行灌注。

2.3.2 复合材料方管VARTM成型实验分析

在复合材料方管VARTM灌注成型中，通过大气压与真空压力差将树脂灌注到柔性真空袋内部的单向和三维编织混杂预成型体中，保持出胶口真空状态，观察树脂流动前沿的位置，通过使用相机记录整个树脂的灌注过程，并与PAM-RTM软件得到的树脂灌注仿真模拟结果进行对比，结果如图10所示。

图10 基于VARTM的复合材料方管树脂灌注过程仿真模拟和实际成型Fig. 10 Simulation and actual forming of resin infusion process in composite square tube based on VARTM

从图10的复合材料实际制备和仿真模拟结果对比中发现，在相同的灌注时间下，实际灌注中的树脂流动前沿位置要慢于仿真模拟中的树脂流动前沿位置，灌注时间为92 s时，由于时间较短，观察不明显，但从灌注2 124 s和模拟灌注结束3 897 s可以明显看出实际灌注较慢，最终实际灌注所用时间为4 052 s，误差约为3.8%，在合理的误差范围内[22]。而实际灌注的树脂流动前沿相较于仿真模拟延后，可能是因为实际灌注的真空压力并不能像仿真模拟保持绝对真空，也有可能是因为在织物铺层时制件棱边处织物发生变形导致三维编织织物编织角变化引起纤维取向变化，造成实际灌注时间较长。另外，从3 897 s的填充仿真模拟结果看出，模型完全被填充，没有缺陷。

图11为复合材料方管的固化脱模。将完成灌注的复合材料方管置入烘箱中，设置固化程序进行加热固化，固化完成后待自然降温冷却到室温后方可脱模，将泡沫模具处理干净后可得到复合材料方管。观察发现，复合材料方管表面没有产生明显的缺陷，与仿真模拟得到的结果一致，说明仿真模拟对复合材料方管实际的树脂灌注具有一定的指导性和可靠性。