基于特征构造和改进PSO算法的分布式光伏功率预测
2024-03-10孟令哲曾新华庞成鑫
孟令哲,周 翔,曾新华,庞成鑫
(1.上海电力大学电子与信息工程学院,上海 200090;2.复旦大学工程与应用技术研究院,上海200433)
大多数分布式光伏并没有完善的天气数值测量、卫星云图以及预报系统[1-2],相比集中式光伏电站,功率预测难度较大。文献[3]利用聚类方法进行天气分类,文献[4]采用多种天气融合进行预测。相比集中式光伏电站,分布式光伏历史数据量较少,天气分类进一步缩减可用数据,导致预测精度不高。
针对以上问题,建立了基于聚类算法的特征工程,聚类的指标以及结果作为新的特征,以扩大分布式光伏数据集的样本规模;提出改进粒子群优化算法(PSO),该改进算法基于一种跳出循环策略,确保PSO 算法避免局部最优情况发生,向全局最优方向迭代,并应用于模型超参数优化中。
1 分布式光伏数据预处理
采用拉依达(3-Sigma)准则[5]来判断异常数据,并对异常数据进行插值处理。分布式光伏输出功率数据一般服从Beta 分布或者正态分布[6],认为测量数据x和平均数据μ之差若超过3 倍的标准差δ,则判定为异常数据,如式(1)所示,将原始数据压缩到[0,1]范围内,最后预测时反归一化处理。
2 相关性分析及特征构造
只考虑光伏出力不为0 时刻的点,由于各个环境变量对分布式光伏输出功率各不相同,应对整个数据相关性进行分析,以便于模型的降维处理,减少计算时间。每个环境变量序列与光伏输出功率相关性计算公式如式(2)所示:
式中:R(Xj,Xk)为相关性系数;Cov(Xj,Xk)是两个向量的协方差;Var(Xj)和Var(Xk)是两个向量各自的方差。
引入二分聚类算法对原始数据进行聚类,相比于传统k-means 聚类算法[7]能克服陷入局部极小值的情况。聚类后的每个数据都会有一个欧氏距离的数据特征,该数据点是每个时间点的所有欧氏距离,欧氏距离计算公式如式(3)所示:
式中:d(x,y)是欧氏距离;xi是归一化后特征;yi是归一化后的光伏出力。该公式描述了与集群中心点的距离,中心点指的是典型天气情况下的输出功率和气象因素之间的关系。每个时间点计算的欧氏距离作为独立输入特征,引入到数据集训练,其机理相当于先于模型训练前,分析输入和输出的相关性,该相关性指标纳入到训练模型中,再引入聚类结果的特征。由于分布式光伏的数据可能没有明确天气的特征,所以无法进行传统的典型天气如晴天、阴天、雨天的划分,若采用聚类算法划分,则无法说明该类别是否属于某种典型天气,而只能说明归类结果。扩充后的数据集再进行监督学习,因此,本构造方法的训练特征增加二维,分别为聚类结果及欧氏距离,可用数据增加,能够解决分布式光伏测量系统测量数据少的问题。
3 网络模型
为了保留数据时序性,所提出的单步预测模型以长短时记忆网络(LSTM)为基础,引入注意力机制在LSTM 之后分配权重,提出改进后的PSO 算法作为网络超参数的优化,并采用由序列到监督的学习方法。
3.1 LSTM 循环神经网络
LSTM 在1997 年由Hochreiter 和Schmidhuber 所提出,是一种适合处理时间序列连续性的网络,相比于循环神经网络(RNN)会出现陷入梯度消失和爆炸的情况,LSTM 网络能够解决长期依赖的问题[8]。LSTM 网络的一个单元结构如图1 所示。
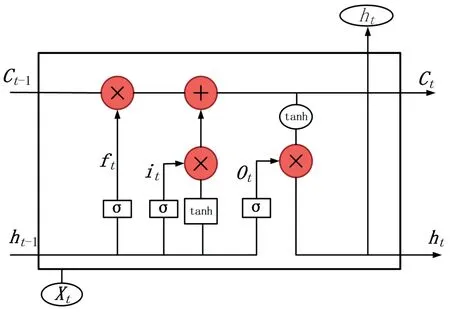
图1 LSTM单细胞结构
3.2 引入注意力机制的网络模型
注意力机制是一种人类视觉反映到大脑而产生不同关注点的机制。现有如LSTM 模型之类的模型虽能学习输入与输出相关性,但无法准确关注到各个输入对输出的影响程度大小,而注意力机制相当于对输入值进行一个权重的分配,其它模型如BP 神经网络与注意力机制的结合在处理长序列的任务时表现并没有LSTM 结合注意力机制好。因此,将注意力机制与LSTM 模型相结合进行分布式光伏预测,所提模型的框图如图2 所示。
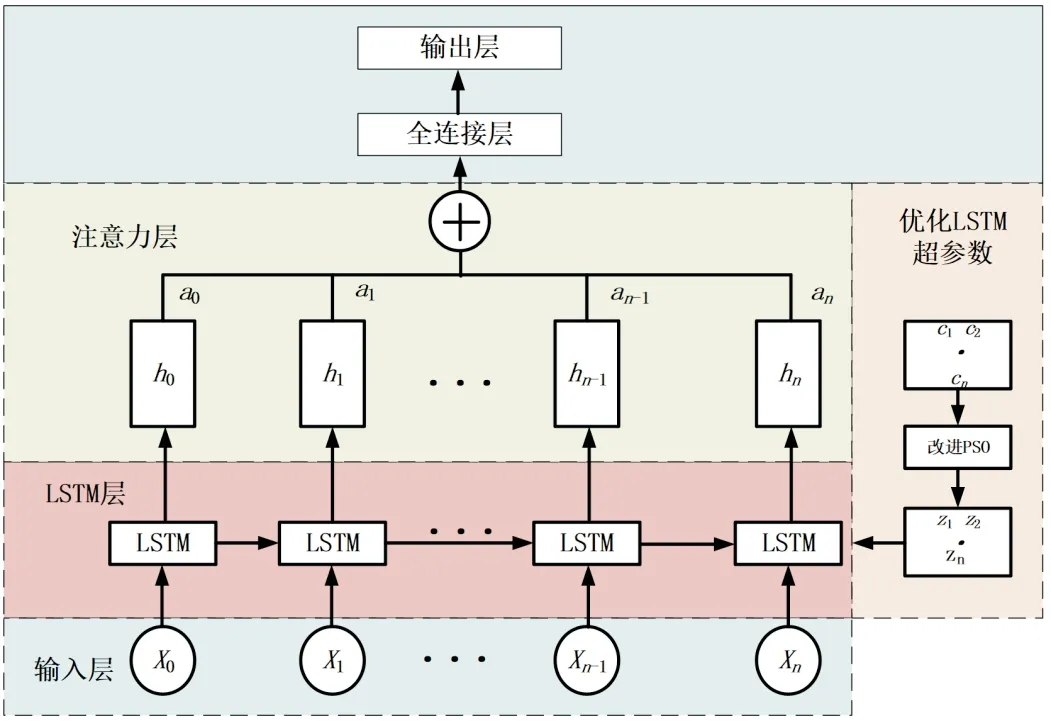
图2 网络模型框图
X0~Xn为输入网络模型的历史数据,包括气象数据、历史输出功率,称为输入层。该数据流过LSTM层进行特征提取学习,其中,利用改进的PSO 算法优化整个LSTM 网络的超参数,优化的参数结果返回到LSTM 层中。在注意力层中,h1~hn为输入序列的状态值,进行相似性判断后求两者向量点积,按概率赋予各部分之间的权重a1~an,赋予较强特征较大的权重,反之同理,根据权重系数,对h1~hn加权求和,使得模型对强特征的表达能力更强,最后,数据通过全连接层输出预测结果。
3.3 改进PSO 的超参数优化
使用粒子群算法进行超参数优化,共进行维度为3 的超参数优化,控制变量为抓包数大小,LSTM隐藏层神经元大小,正则化率。目标函数如式(4)所示,该公式反映了预测值与真实值的差值比之和,数值越小,说明模型拟合程度越高。
式中:predict为光伏输出功率预测值;true为真实值。
针对标准粒子群算法存在容易陷入局部最优的问题[9],本文提出一种改进的PSO 算法,用于在循环中跳出局部最优点,并进行下次迭代。标准PSO 算法出现局部最优的原因主要有以下两点:(1)粒子速度衰减较快,导致粒子在迭代到一定代数的过程中,速度太小,无法进行搜索更新;(2)对于某些复杂问题,虽然粒子速度没有明显衰减,但是被更新到最优位置的概率大大减小。
为了解决陷入局部最优的问题,提出以下策略:每次迭代时,当获得一个局部最优位置,则对所有粒子的位置进行编码成一个向量,对此时的粒子进行聚类,聚类中心点随迭代次数增加而减少,防止迭代刚开始时,粒子最优位置不清晰,错误选择最优位置,但必须选择以每次迭代的局部最优位置作为一个中心点,也即加入先验知识,如果局部最优聚类簇数小于某一个中心点聚类簇数,则保存全局最优到一个数组当中,引入变异策略,按照一定概率,当变异值大于0 且数组不为空集,则自行随机选择数组中的元素作为全局最优,否则就初始化粒子和种群。由于数组中的粒子都是历史的最优值,再次选择时可以提高粒子速度,同时,初始化会重新生成最优值,避免一直在局部最优值下迭代。为了实现快速优化,获得全局最优和局部最优之间最佳平衡,引入自适应惯性权重ω,公式为:
式中:ωmax和ωmin是惯性权重的最大值和最小值;f为目标函数值;favg为平均值;fmin为最小值。
ω用来控制粒子的速度大小,ω大时,由基本PSO 更新公式知,全局搜索能力强;ω小时,粒子速度减小,局部搜索能力强。当每个粒子测量到的光伏输出功率误差基本一致时,粒子速度变小,则陷入了局部最优,此时优化得到的优选变量为非最优值,导致LSTM 网络参数设置不合适,最终使得预测质量降低。由式(5)可知,引入的自适应惯性权重ω增大,增大了全局搜索能力,避免了继续朝着局部最优处更新粒子,粒子全局最优得到更新。
3.4 评价指标
本文采用的评价指标共有三种:均方根误差(RMSE)、平均绝对误差(MAE)、拟合度[10]。RMSE与MAE均反映了预测值与真实值的偏差程度,拟合度的值越接近1,说明模型拟合效果越好。三种评价指标的公式如下:
式中:RMSE、MAE、R2均为模型评价指标;Pi为第i时刻光伏发电功率的真实值;P'i为第i时刻光伏发电功率的预测值;Piav为发电真实值的平均值;n为测试集的总时刻。
3.5 总流程
图3 为神经网络预测光伏功率流程图,数据预处理包含了数据的清洗。利用聚类算法,生成聚类结果及欧氏距离作为新特征扩充数据集。特征工程构造完毕后,归一化数据进行监督学习,划分为训练集、测试集以及预测集三类。在训练集中,经过3.3节的算法,在该算法循环中初次训练网络模型,根据适应度函数得到最优超参数,在测试集应用最优超参数进行训练,输出评价指标来判断该模型的性能。预测集用于输出归一化的预测值,反归一化预测值后,最终输出预测结果。
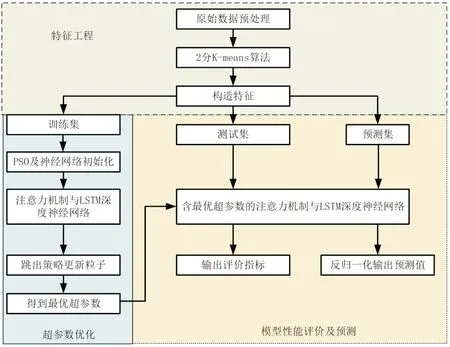
图3 神经网络预测光伏功率流程图
4 实验分析
本研究的目的是在数据量少的情况下,预测分布式光伏电站的发电量,所用数据集为澳大利亚公开光伏数据集(DKASC),包含了分布式光伏的输出功率以及各类气象因素,原始数据有全局辐射水平、温度、相对湿度、漫反射水平、风速、降雨量、相位。采用平台为python3.8 版本。将数据进行异常数据的检测和归一化处理后,构造特征工程并融合数据集。测试集选取了一天内150 个输出功率不为0 的时间点,用于直观反映预测效果。训练集与测试集之比为7∶3。
由式(2)计算得各因素相关系数为:全局辐射水平0.903、温度0.423、相对湿度0.556、扩散水平辐射0.117、风向0.001、降雨量0.362 2、电流0.996,欧氏距离特征相关系数为0.574 6,聚类结果特征相关系数为0.481 1,与输出功率有较高相关性,证明了所提特征构造方法有效。由以上分析可知,风向及扩散水平辐照度与光伏输出功率的相关性最小,该类特征不应作为模型的训练特征。
改进PSO 的初始化参数,设置为迭代次数90 次,加速因子C1为2,C2为3,惯性权重最大、最小值分别为0.7 和0.3,粒子数50 个,搜索维度为3 维。目标函数如式(4)所示,优化迭代曲线与未优化迭代曲线如图4 所示,标准算法在迭代至16 代时,算法开始有一个较长时间的收敛,而改进后的算法在第78 代后才收敛,这是由于收敛速度与收敛计算时间存在矛盾。改进后的算法由于其粒子初始化的原因,导致在经过局部最优时重新迭代,算法收敛速度下降。改进后的迭代曲线上有两次适应度函数迅速增加,这是由于跳出循环策略的引入,选择了历史最优值或者粒子初始化,从而跳过局部最优,经过两次突变后,目标函数继续下降,并最终收敛,而标准的PSO算法,停靠在局部最优处不再收敛。改进的PSO 算法从初始目标函数值的2.4×1010降至1.4×1010。标准PSO 算法从初始目标函数值的2.6×1010降至2.2×1010。
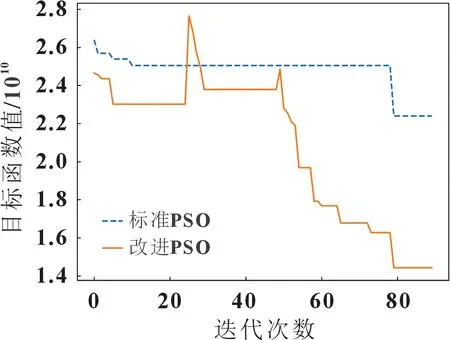
图4 粒子群算法优化曲线对比图
优化超参数的初始值和寻优范围如表1 所示。最终的优化结果是神经元数量为57,dropout 比率为0.015 64,Batch size 为34。在此超参数下,固定模型的训练效果最好。
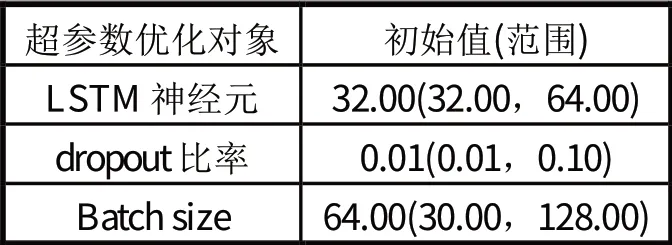
表1 超参数优化值
表2 展示的是不同超参数的取值,进而形成的评价指标。初始超参数均取表1 中的初始值。由表2可以看到,改进后的PSO 算法相比标准PSO 算法优化LSTM 网络超参数后,RMSE、MAE均下降,而预测精度提升。说明与标准算法相比,改进算法的收敛性更好,找到了更能满足目标函数最小值的控制变量,而结合图4,标准算法的适应度函数已经在第15代趋于稳定不再收敛,因此可以说明该算法陷入了局部最优,而改进后的算法无论在适应度函数曲线上下降方面,还是在优化超参数使得模型性能得到提升方面,均证明了所提改进效果的有效性。
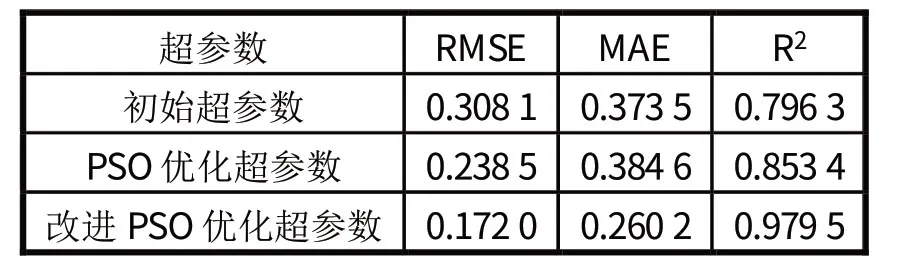
表2 不同超参数对性能指标的影响
网络模型共有4 层,包括2 个LSTM 层,一个注意力层以及一个全连接层。较高的学习率会增加丢失先验知识的风险,因此引入了学习率自适应调整策略,每经过10 次迭代,学习率降低为原来的1/10,初始学习率为0.01,采用Adam 优化器。
图5 展示了预测结果的对比,所提模型采用注意力机制与LSTM 网络结合,且采用改进的PSO算法进行超参数的优化,LSTM 模型是指去除超参数优化及注意力机制预测的结果。总体来看,相对于LSTM 模型,所提模型的预测值与真实值更接近,曲线较为平滑,预测效果良好。在光伏出力较高的时间点,与真实值贴合更紧密,表明模型可以准确预测高出力点的值。在光伏出力趋势波动较大时,LSTM 模型预测极端变化点的输出功率结果相比实际值会偏高,而所提模型在极端点的预测与真实值几乎一致。
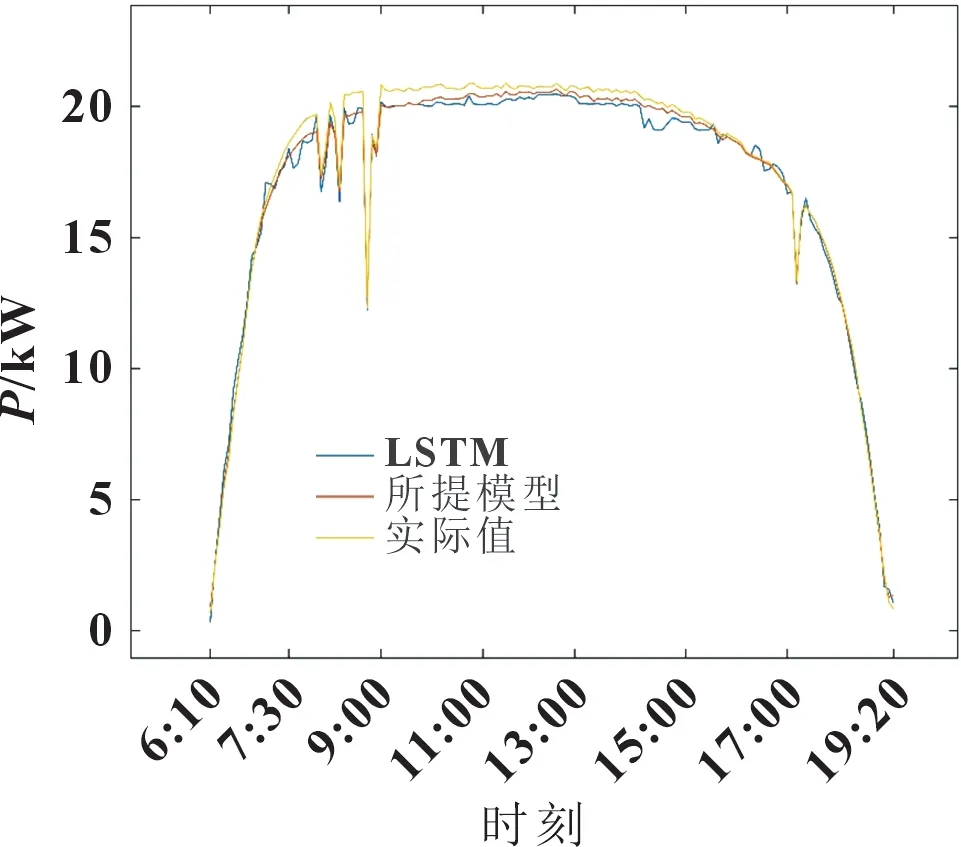
图5 分布式光伏总预测曲线
表3 是不同方法评价指标的数据。每次实验和迭代由于寻优各有差异以及模型的学习效果不同,数据均有变化,最大变化率不足5%,各种方法和模型下的实验均进行5 次,取平均值。

表3 预测方法评价指标对比
方法一是简单LSTM 监督模型,其中超参数为初始参数;方法二引入聚类算法构造特征,扩充数据集;方法三引入了注意力层;方法四引入改进PSO 算法优化超参数。随着模型深度增加,RMSE与MAE评价指标均依次降低,R2指标均依次升高,说明模型的拟合效果较好。构造特征后,RMSE及MAE均有较大幅度降低,这是由于原始数据被扩充后,网络模型提取了更多有用信息,同时,各个特征的相关性信息也被充分提取。相比于方法三,方法四的评价指标改善情况显著,这是由于超参数的选择可以改善模型性能,而优化超参数会让固定结构的模型把性能发挥到极致。
表4 对比了不同神经网络对评价指标的最终影响,均采用特征工程以及使用优化算法进行超参数自动调优。从表中可以看出,LSTM 的评价指标优于其他三类神经网络,而Bi-LSTM 网络与LSTM 网络的评价指标接近,且只有对于MAE,Bi-LSTM 低于LSTM,因此选用LSTM,而不选用Bi-LSTM 网络是合理的。可以看到,相比于BP 神经网络,RNN 性能有较大的提升,这是由于RNN 神经网络具有时序性,相比BP 神经网络能够更好处理时间序列。

表4 预测模型评价指标对比
5 结论
本文提出了一种基于数据分析和挖掘的神经网络模型,应用于分布式光伏历史数据有限输出功率的短期预测场景。基于欧式距离的特征工程的构造方法,新特征与输出功率之间存在较强联系,最终在预测评价指标上表现较好。同时,为了让模型更加关注到与输出功率存在强联系的数据,引入了注意力机制到LSTM 模型当中。实验证明,模型评价指标R2相比于简单模型进一步提高,最终拟合度接近98%。提出了一种避免PSO 算法陷入局部最优的策略并应用于神经网络的超参数自动寻优,该策略是经过一个局部最优的判据后,选择初始化粒子或者更新粒子跳过局部最优点,实验证明,相比标准的PSO 算法,适应度曲线突起后大幅度下降,避免出现局部最优不再收敛的情况。
