基于相关性的大型救援装备模块划分方法

赵 京, 张晓丹, 张自强, 苗 磊

(北京工业大学材料与制造学部, 北京 100124)

我国国土面积辽阔,地质条件复杂,是受到地震、泥石流、滑坡等重特大自然灾害影响最为严重的国家之一,应急救援装备在灾害救援中发挥着至关重要的作用[1-4]。 但当灾害发生时,对于边远山区、交通闭塞的情况,大型救援装备因体积、质量大,在道路桥梁损毁严重、陆地运输受阻时难以快速运抵灾害现场。当前,模块化技术逐渐成为复杂机械装备的发展趋势之一[5-7],可以帮助大型救援装备进行“大转小”设计制造和转运,通过建模分析模块的划分方案及快速拆装结构,在保证结构可靠性的前提下控制较小的模块体积和质量,优化模块拆装时间,形成快速拆装的模块化救援装备,可在灾时分模块拆解,使用空运抵达灾害现场,并在现场高效组装快速投入抢险救灾,极大提高救援效率,减少人员伤亡和财产损失。因此,模块化技术成为解决大型救援装备灾时转运和投用效率问题的有效途径和必然趋势[8-9]。

模块化是指以模块为基础,综合了通用化、系 列化、组合化的特点,解决复杂系统类型多样化、 功能多变的一种标准化的高级形式[5]。当前,已有众多学者针对机械装备提出了各类模块化设计及划分方法[10-12],例如,文献[13]针对机械产品的产品族,提出了模块化产品配置设计方法,文献[14]面向产品的生命周期,通过构建产品描述模型提出了一种有效性驱动的模块聚类方法。现有这些方法主要考虑了快速响应市场需求,能够有效降低产品的研发和维护成本,取得了一定的研究成果。

然而,目前的这些模块化方法对于救援装备的特殊场景并不适用,未考虑救援装备模块运输便利性问题,也未对模块拆装作业效率等问题进行探究。这些问题正是救援装备模块化需要考虑的首要问题,而目前在救援装备的模块化理论方法方面存在空白。因此,本文针对大型救援装备,提出了一种基于零部件相关性的模块划分方法,有助于实现救援装备的模块化运输和灾害现场快速拆装,解决大型救援装备在灾时的转运和投用效率问题。

1 零部件相关性评价

模块化的本质就是将一个系统中具有相似或相关功能和结构的部分聚合在一个模块中,形成模块内高内聚、模块间低耦合的系统状态[13]。在本文中,则是评价救援装备零部件之间的相关性,即零部件之间的联系紧密程度,据此将零部件聚合在不同的模块中。

1.1 指标体系构建原则

大型救援装备是一个复杂的机械系统,其零部件之间的相关性维度多,关系复杂,构建相关性评价指标体系应当按照一定的原则执行。本文在一些通用原则的基础上,结合模块化救援装备在灾时救援场景的特殊需求,确定了构建相关性指标体系的几个原则:

1) 整体性原则。应保证相关性指标体系应能够全面反映零部件之间的相关性,进而保证基于此相关性进行的模块划分最合理。

2) 独立性原则。同一层次内的评价指标之间应当是相互区分、相对独立、互为补充的关系。

3) 可行性原则。应当考虑数据采集的可行性,合理设置指标,使得指标评价切实可行。客观指标数据应当容易获取,主观指标应当明确评价标准。

4) 拆装便捷性原则。对于救援装备,本文致力于实现其模块的便于运输和快速拆装,因此各相关性指标均应当服务于衡量零部件之间的拆装便捷性。

5) 精简性原则。指标体系应当在满足整体性原则的同时以拆装便捷性原则为核心目标,减少其他无关的冗余指标项,使指标体系对救援装备有足够的针对性且足够精简,以减少数据量。

6) 客观性原则。应当尽可能设置客观的评价指标,以客观直接可测的数据,或行业公认的技术指标等作为相关性评价指标,一方面可以减少专家评价数据量和工作量,另一方面可保证相关性评价数据的精确性和客观稳定性。

1.2 相关性评价指标体系

有专家学者在机械装备的模块化设计中提出了一些评价零部件相关性的指标[15-17],但这些指标较为宏观,定性指标居多,难以精确量化,且未关注模块的拆装便捷性,难以针对救援装备满足特殊需求。因此本文参考这些指标,在前述的构建原则基础上,通过装配车间调研、咨询技术专家等方式,针对救援装备确定了如图1所示的零部件相关性评价指标体系。

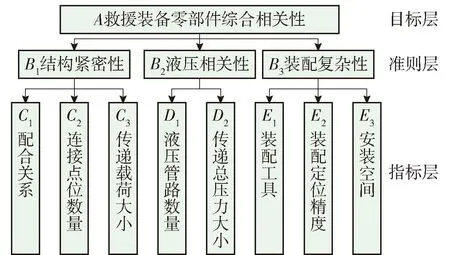
图1 救援装备零部件相关性评价指标体系Fig.1 Correlation evaluation index system of rescue equipment components

按照客观性原则,在指标体系中尽可能地设置了客观定量指标,例如指标C2、D1和D2完全不依赖专家主观经验,具有绝对的客观性;一些指标如C1、E1和E2等建立在客观的技术数据基础上进行评价,也具有较高的客观性。表1列出了各相关性指标的评价标准,按照此标准,即可对救援装备各零部件间各指标的相关性进行评价,得到0～1的相关性得分。

表1 相关性评价标准

1.3 层次分析法确定指标权重

指标的权重系数反映了各指标对总目标“综合相关性”的贡献程度,即将来模块划分时被重视的程度,直接影响到模块划分结果的科学性。层次分析法(principal component analysis, AHP)[18]是一种简洁高效的确定权重系数的方法,本文采用层次分析法来确定各指标权重,能够较好地反映专家意图,即模块划分时对各相关性指标的重视程度。

经过专家咨询和计算,得到各层次指标的权重及各指标项对于目标层的综合权重,如表2所示。因此,相关性指标体系中各指标项对于目标层的综合权重向量为

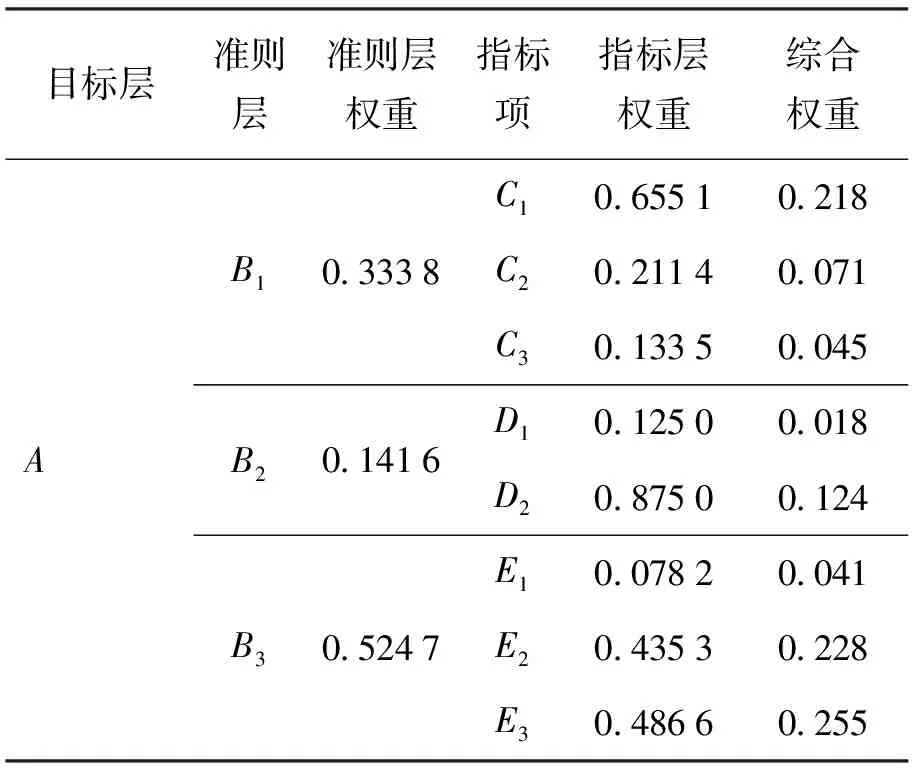
表2 指标权重

W*=(0.218,0.071,0.045,0.018,
0.124,0.041,0.228,0.255)T

1.4 综合相关性矩阵

对于指标体系中的每个指标项Ik(k=1,2,…,8),救援装备的所有零部件C={C1,C2,…,Cn}(n为零部件总数)按照表1的评价标准两两分析相关性,可以得到若干个相关性矩阵:

Rk=[krij]n×n

式中:krij为零部件Ci和Cj在指标Ik上的相关性。显然,0≤krij≤1,且krij=krji,当i=j时,krij=1,该矩阵为对称矩阵。

(1)

式中:rij为零部件Ci和Cj之间的综合相关性。rij的值越大,表明两零部件之间具有整体越强的相关性,未来将更有可能聚合在同一模块中。显然0≤rij≤1,R也是对称矩阵。

2 模块聚类分析

基于综合相关性矩阵R,采用聚类算法逐步将相关性较强的零部件聚合在同一模块中即为模块的聚类分析过程,聚类结果即为模块划分结果。

2.1 层次聚类算法及其改进

在当前互联网时代,发展了大量的数据聚类算法[19-20]用于数据分类、数据分析等领域,但这些方法大多都需要改造才能应用于机械零部件的模块聚类分析,而针对救援装备特殊的救援场景应用需求,尚没有发展出可用的方法。本文在分析对比常用的聚类算法后,选择了Tang等[21]提出的一种基于商空间理论的层次聚类算法作为基础,并针对救援装备进行改进。

层次聚类算法是一种常用的数据聚类分析方法,该算法无须指定聚类数目和聚类中心等参数,无须通过坐标计算距离,基于相关性矩阵即可直接进行聚类,适合本文进行救援装备零部件的聚类。Tang等的算法在普通数据集的聚类中有较好表现,但针对救援装备的特殊需求还需要进行改进,下面简要介绍改进后的算法。

对于救援装备的零部件集C={C1,C2, …,Cn},有综合相关性矩阵R=[rij]n×n,可求得归一化距离矩阵:

D=[1-rij]n×n=[dij]n×n

式中:dij为零部件Ci和Cj之间的归一化距离,0≤dij≤1,其值越小,距离越近,则越有可能将两零部件聚在同一簇中。

令集合

Λ={dij}={λ0,λ1,λ2,…,λp}

式中:p为矩阵D中各不相同的元素个数;λi(i=1,2,…,p)为矩阵D中各不相同的元素之一,称为粒度,且有0=λ0≤λ1<λ2<…<λp。

设限制单个模块质量最大值为mmax,记m(Mi)为模块Mi的总重,记d(Mi,Mj)为模块Mi与模块Mj之间的相关性距离。通过以下算法,即可生成救援装备零部件的层次聚类结构。

步骤1i⟸0,A⟸∅,M={M1,M2,…,Mn}={{C1},{C2},…,{Cn}}。

步骤2输出X(λ0)=M。

步骤3i⟸i+1,A⟸M,M⟸∅。

步骤4Mtemp⟸∅。

步骤5取质量最大的模块Mj∈A,Mtemp⟸Mtemp∪Mj,A⟸A-{Mj}。

步骤6按质量从小到大遍历Mk∈A:

步骤6.1 若m(Mtemp∪Mk)≤mmax,转步骤6.2,否则转步骤7;

步骤6.2 若d(Mj,Mk)≤λi,Mtemp⟸Mtemp∪Mk,A⟸A-{Mk}。

步骤7M⟸M∪{Mtemp}。

步骤8若A≠∅,转步骤4;若A=∅且M≠X(λi-1),输出X(λi)=M。

步骤9若i=p或M={{C}},转步骤10;否则转步骤3。

步骤10结束。

相比于Tang等的算法,主要的改进如下:在步骤5中,取集合A中质量最大的模块Mj作为后续步骤的聚类中心,在步骤6中,按质量从小到大的顺序逐个操作模块,先判断模块质量是否超出限制,然后计算两模块之间的相关性距离,若距离足够近,则聚集在同一模块中。通过这些调整,使得算法倾向于以质量较大的零部件(模块)作为聚类中心,从最小质量的零部件开始向中心聚集,可以有效保证中心零部件的核心特性,避免质量较小的零部件剩余在最后,导致划分不合理的情况。

此外,算法中模块Mi与Mj之间的相关性距离d(Mi,Mj)有3种度量准则[22]可以选择,如表3所示,将生成不同的层次聚类结构。

表3 模块间相关性距离度量准则

经过上述算法,即可生成救援装备零部件的层次聚类结构{X(λi)|∀λi∈Λ},其结构示意如图2所示,该层次聚类结构的每一层,都代表着一种模块划分方案,自底向上聚类,粒度λi值越来越大,代表着其对应层次的零部件聚类(模块划分)结果粒度越来越粗,模块数量越来越少,单个模块内部零部件数量越来越多。

图2 层次聚类结构示意Fig.2 Schematic diagram of hierarchical clustering structure

2.2 非均匀粒度聚类

前面提到,图2中每一层代表的模块划分方案中每个模块的粒度都是相同的,然而每个模块中零部件之间的相关性却各不相同,一般认为这样的模块是粗糙的[23],将会导致未来的优化目标函数产生突变,不利于后期的评价和优选。非均匀粒度聚类能够弥补上述均匀粒度聚类的不足,本质是将上述层次聚类结构中每一层中的模块取并集,得到所有模块的种类,然后排列组合就能使不同粒度的模块出现在同一模块划分方案中[13,24],如图3所示。

图3 非均匀粒度聚类示意Fig.3 Schematic diagram of clustering with non-uniform granularity

例如,对于前述救援装备零部件层次聚类算法生成的层次聚类结构:

{X(λi)|∀λi∈Λ}

每一粒层X(λi)包括mi个模块Mj,即

X(λi)={M1,M2,…,Mmi}

将所有粒层取并集即可得到该聚类结构中所有的模块组成的集合:

(2)

同时,由于采用3种不同的模块距离度量准则,可以生成3种不同的聚类结构及其模块集合MS、MC和MA,因此可以将这些模块全部收集起来,得到 3种模块距离准则下聚类生成的全部模块的集合,即

M=MS∪MC∪MA

(3)

3 多目标优化

对于救援装备的模块集合M,将这些模块进行排列组合,组成一个完整的装备即为一种非均匀粒度聚类的模块划分方案。但当模块种类较多时,排列组合数量呈指数级增长,难以枚举出所有可能,需采用优化方法,从中选择出最优模块划分方案。

本文研究的重点在于模块划分的方法,而对于优化方法,本着成熟、便捷、稳定的原则,本文直接采用遗传算法[25]进行求解,其运行过程不再赘述,下面介绍其在本文优化问题应用上进行适应性改造的几个重点环节。

3.1 多目标优化模型

3.1.1 问题描述

对于救援装备全部模块的集合:

M={M1,M2,…,Mm}

式中m为生成的模块总数。

每个模块包含救援装备中的若干零部件,即

Mi={Cj|∀Cj∈C}

通过对这些模块进行排列组合,可以得到若干模块划分方案,每个模块划分方案可以表示为

X={Mi|∀Mi∈M}

因此,模块划分方案的多目标优化可以表述为:以模块集M为基础,进行选择和排列组合,得到若干模块划分方案X,选择其中满足指定优化目标的一个最优方案X*,作为救援装备的最优模块划分方案。

3.1.2 优化目标

1) 耦合度

定义两模块间的耦合度为两模块之间存在的两两零部件综合相关性的平均值,则将方案X中两两模块间耦合度之和——“整体耦合度”作为极小化目标函数F1(X),其公式可以表示为

(4)

耦合度主要反映方案中模块之间的联系紧密程度,能够间接反映模块拆分的可行性,以及将来进行模块装配的难度和耗时情况。

2) 内聚度

定义模块内部的内聚度为模块内部各零部件间的综合相关性之和,则将方案X中所有模块的内聚度之平均值——“平均内聚度”作为极大化目标函数F2(X),其公式可以表示为

(5)

内聚度主要反映方案中各模块内部零部件之间的联系紧密程度,即不可分程度。

3) 粗糙度

定义模块的粗糙度为模块内部各零部件间综合相关性的方差大小,反映模块内部相关性的离散程度及模块的粗糙程度,则将方案X中所有模块的粗糙度之平均值——“平均粗糙度”作为极小化目标函数F3(X),其公式可以表示为

(6)

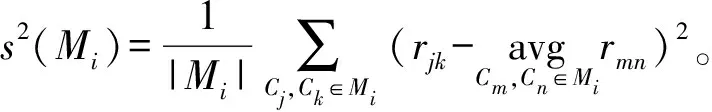
粗糙度主要反映方案中各模块内部零部件之间关系的一致性,间接反映出聚类的合理性和模块的稳定性。

4) 模块数量

救援装备拆分的模块数量尽可能少,从而降低救援装备的转运成本和装配难度。因此将模块划分方案X中的模块数量作为极小化目标函数F4(X),其公式可以表示为

minF4(X)=|X|

(7)

模块数量可以在一定程度上反映该方案在灾时转运和装配投用的效率。

式(4)～(7)中:rjk表示零部件Cj和零部件Ck的综合相关性,可以由式(1)求得的综合相关性矩阵R查得;|Mi|表示模块Mi中的零部件个数;|X|表示方案X中模块个数。

上述4个目标函数的权重系数可由AHP法求得,过程略,权重向量为

w=(0.275,0.387,0.14,0.198)T

3.1.3 约束条件

由于模块排列组合方式随模块数量呈指数增长,而其中的大部分排列组合方式并不能正确组成完整的救援装备,因此需要一定的约束条件限制可行解的范围。对于一种模块划分方案X,需要确保其中的各模块能够不多不少地恰好包含救援装备的所有零部件。即对于一个模块划分方案X={Mi|∀Mi∈M},其包含的若干模块Mi应当满足

(8)

3.2 染色体二进制编码

本文优化问题的自变量是模块的排列组合,本质上可以转换为方案中各模块的有无,因此染色体可以采用二进制进行编码。

首先对模块进行编码。对于一个模块Mi={Cj|∀Cj∈C},使用布尔向量mi来代表该模块:

mi=(c1,c2,…,cj,…,cn)

其中:

按照上述规则对模块集M中的每个模块进行编码,得到m个布尔向量mi,按照特定的顺序将其按行排列,形成布尔矩阵:

矩阵Z称为救援装备零部件与模块之间的构成矩阵。

然后对模块划分方案进行编码。对于方案X={Mi|∀Mi∈M},使用布尔向量x进行表示:

x=(x1,x2,…,xi,…,xm)T

其中:

这样的向量x即可表示方案X的染色体。

根据上述二进制编码,可以将约束条件式(8)写作线型方程组的形式:

(9)

3.3 染色体规范化调整

由于遗传算法中的交叉和变异具有随机性,为使交叉和变异之后的染色体x仍然满足约束条件式(9),避免无效个体遗传至子代,需要根据某些规则对染色体进行规范化调整。文献[13]中简要介绍了一种类似的调整方法,本文的方法略有不同,步骤如下。

1) 关闭冲突基因

首先定义2个概念:若∃Ct∈C,有Ct∈Mi且Ct∈Mj,则称模块Mi与Mj冲突。对于染色体x=(…,xi,…,xj,…)T,若基因xi=xj=1且模块Mi与Mj冲突,则称基因xi与xj冲突。

若染色体x存在基因冲突,则应保持交叉片段或变异点位基因值不变,将其他片段中的冲突基因值置为0,即可关闭冲突基因,得到新的染色体x′。

2) 查找缺失零部件

关闭冲突基因后,该染色体当前包含的零部件计算式为

c=x′T·Z=(c1,…,ci,…,cn)

式中:ci=1代表该染色体包含零部件Ci;ci=0则代表该染色体缺失零部件Ci。

若缺失的零部件数量较少,可按后续步骤填补缺失的零部件。若缺失数量过多,则说明该个体具有严重缺陷,直接标记为缺陷个体并从种群中移除,从而淘汰掉不利基因的个体,避免无效的优化搜索。

3) 构建缺失零部件和填充模块的构成矩阵

对于构成矩阵Z,取其中一些行,这些行代表的模块仅包含缺失零部件,仅保留这些行中缺失零部件对应的列,即可得到缺失零部件和填充模块之间的构成矩阵:

该矩阵中每行代表一个模块,每个模块中仅包含缺失的零部件,n′为缺失零部件的数目,m′是满足仅包含缺失零部件的模块数目,显然m′≥n′。

4) 求解填充模块组合方式

将矩阵Z′中每行代表的模块进行排列组合,至少有1种方案y=(y1,y2,…,ym′)T可以使得各模块恰好共同提供缺失的零部件。事实上,这与前述的约束条件式(9)类似,求解填充模块组合方式的问题可转换为求线性方程组

的元素均为0或1的解y。

显然,该方程至少有一个可行解,对于多个解的情况,只需随机选取其中一种即可。

5) 调整染色体基因

对于上一步中求解选取的一个组合方式可行解y=(y1,y2,…,ym′)T,取其中等于1的若干元素{yi},找到矩阵Z′中对应的若干行向量{m′i},回溯其在矩阵Z中的位置,即可找到这些行向量代表的模块{Mi}及其在染色体x′中的基因点位,将这些基因值置为1,即可得到规范化调整后的染色体x*,其满足约束条件式(9):ZTx*=(1,1,…,1)T。

4 应用实例

挖掘机具有作业效率高、通用性好、作业功能多样等优势,是抢险救援当中应用最广泛、最主要的大型机械装备之一[26]。完成对挖掘机的模块划分,可为其他救援装备的模块划分及设计提供良好的示范和指导作用。因此,本文将以天津移山YS220液压挖掘机应用本文提出的方法,验证方法的有效性。

4.1 综合相关性矩阵的建立

YS220挖掘机总质量为22 t,体积大,零部件数量多,结构复杂,为减少计算量,避免不必要的模块拆分,本文确定了该挖掘机的27个零部件,作为相关性分析和聚类的最小单元,即零部件集:

C={C1,C2,…,Ci,…,C27}

各零部件的名称及质量如表4所示。

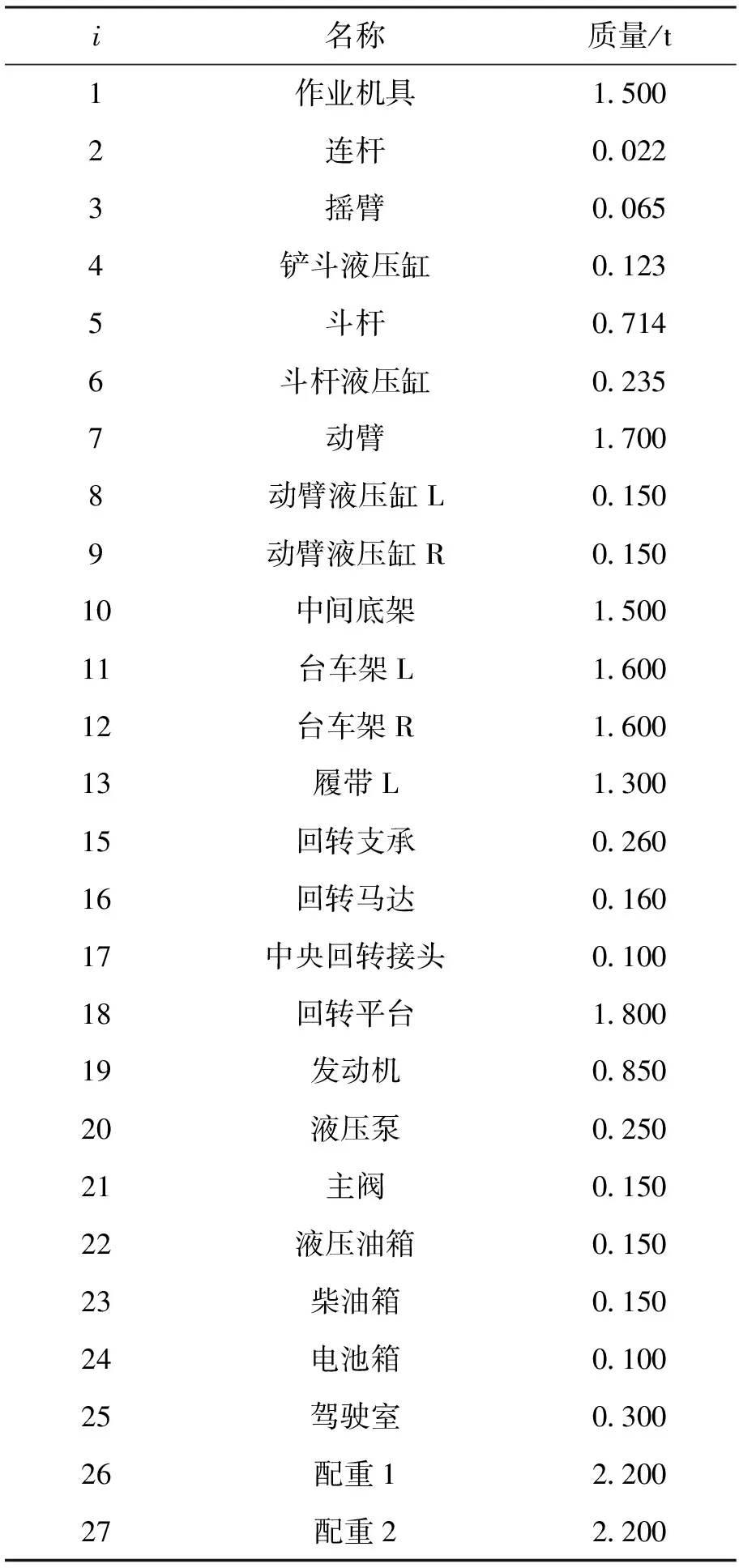
表4 YS220挖掘机零部件集C

按照1.2中提出的相关性评价指标体系,邀请有关专家对每个指标项评价这些零部件两两之间的相关性,得到8个指标的相关性矩阵Rk(k=1,2,…,8),根据式(1)即可求得YS220挖掘机的零部件综合相关性矩阵:

R=[rij]27×27

式中:rij为零部件Ci和Cj之间的综合相关性,具体取值如图4所示,矩阵中值为0的元素已略去。

图4 综合相关性矩阵RFig.4 Comprehensive correlation matrix R

4.2 基于相关性的零部件聚类分析

基于综合相关性矩阵R,应用2.1中介绍的零部件聚类算法,限制单个模块质量最大值mmax=3 t,分别采用3种模块距离准则进行求解,得到3种不同的层次聚类结构,其中部分粒层结果如表5所示。

表5 部分粒层聚类结果

接下来根据式(2)和(3),将3种层次聚类结构中的所有模块放在一个集合中,得到包含所有(共51种)模块的集合M。

4.3 模块划分方案的多目标优化

根据3.2中介绍的二进制编码方案,对模块集M中的所有模块进行编码,并按照一定规则排列,得到YS220挖掘机零部件与模块之间的构成矩阵Z51×27,如图5所示,前27行的分块矩阵为对角阵,且矩阵中值为0的元素已略去。

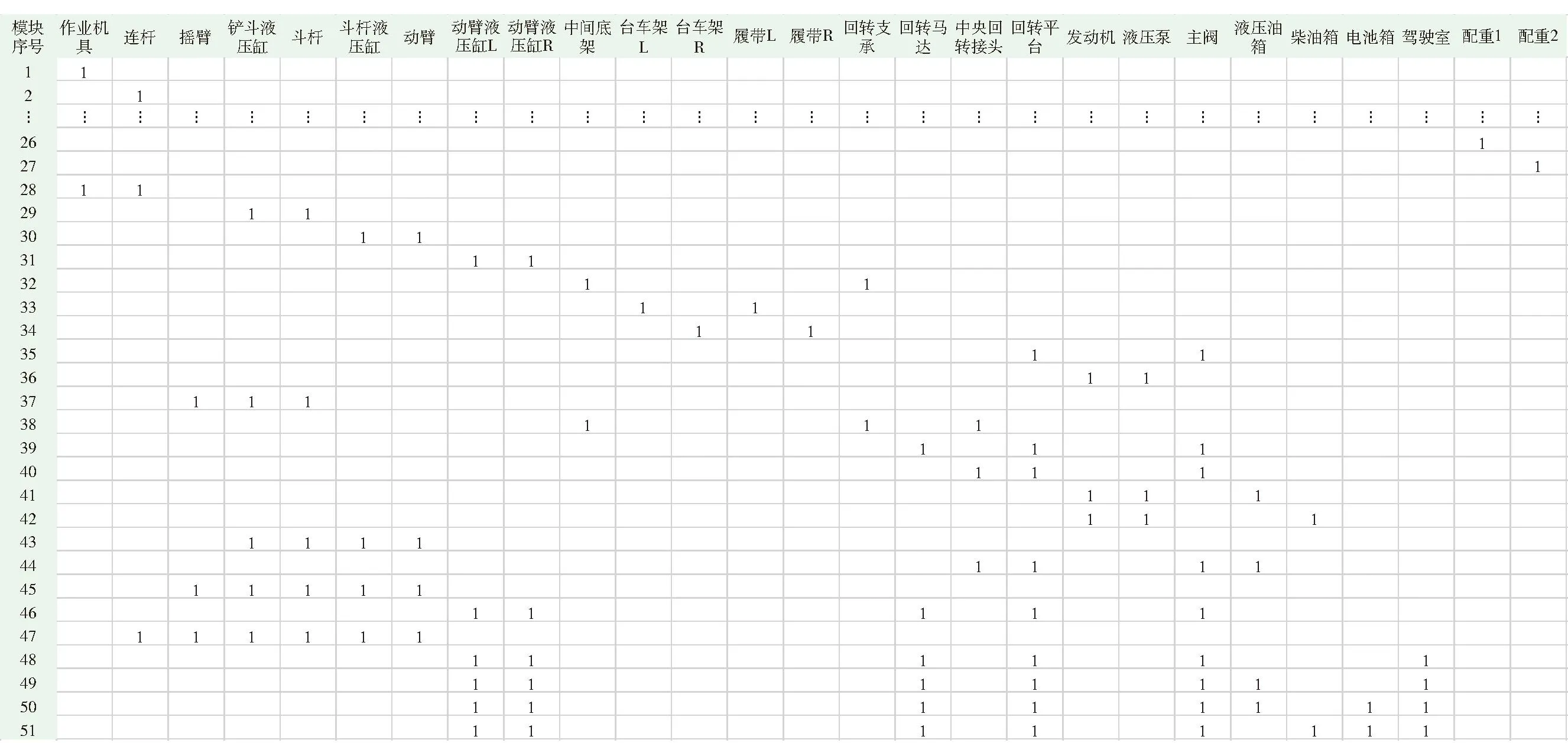
图5 YS220挖掘机零部件与模块的构成矩阵ZFig.5 Composition matrix Z of components and modules of YS220 excavator

对于图5所示的51种模块,理论上有251种排列组合方式,但在式(9)的约束条件下,可行解空间相对较小,在3.3节染色体规范化调整机制的作用下,可保证优化过程在可行解的范围内进行,避免无效搜索影响求解效率。

应用3.2介绍的二进制编码规则,对前述3种层次聚类结构中的每一层方案进行二进制编码,作为遗传算法的初代种群P0,设定交叉概率0.9,变异概率0.2,种群大小20,迭代次数100代,求解得到最优个体x*,对照构成矩阵Z解码,得到YS220挖掘机的最优模块划分方案,如表6所示。最优个体x*的目标函数值分别为F1(X*)=1.019 76,F2(X*)=1.049 79,F3(X*)=0.025 42,F4(X*)=9.0,二进制编码为:

表6 最优模块划分方案X*

10000 00000 00000 00000 00000 11000 00110 00100 01000 01001 0

可以看到,该模块划分方案中每个模块均不超过模块质量限制,模块的组成满足约束条件式(8),方案的整体耦合度低、平均内聚度高、平均粗糙度好、模块数量少。在各项约束和优化目标等方面具有较好的表现,与专家按照经验提出的划分方案相比,避免了专家经验水平的差异性,表现出了更高的效率和稳定性,验证了本文方法的有效性。

5 结论

1) 本文提出了一种基于相关性的大型救援装备模块划分方法。在该方法中:相关性评价数学模型补充了目前针对救援装备零部件相关性评价的空白,能够较全面地反映零部件间的联系紧密程度;通过调整聚类算法的聚类中心和顺序,解决了现有方法聚类结果不稳定、模块划分不合理等问题;对遗传算法进行适应性改造,提出了染色体规范化调整的方法,解决了交叉变异导致的不满足约束条件等问题,使遗传算法能够适用于本文的优化问题。

2) 通过在YS220挖掘机上进行应用验证,结果表明:本文方法能够有效对救援装备进行相关性评价、零部件聚类和方案优化,得到的模块划分结果在各方面均具有较好表现,与专家按照经验提出的划分方案相比,具有更高的效率和稳定性,验证了本文方法的可行性和有效性。该方法为救援装备的模块化设计提供了一种可行的技术路线,在其今后的模块化实践中具有重要指导意义,有助于解决其灾时转运和投用效率的问题。