基于液膜反转的定向井临界携液模型研究
2024-03-08于相东石书强李国良房金伟段传丽齐丹
于相东,石书强,李国良,房金伟,段传丽,齐丹
(1.中国石油渤海钻探工程公司油气合作开发分公司,天津 300457;2.重庆科技大学石油与天然气工程学院,重庆 401331)
气井积液是气井开采中后期面临的一个重要难题,随着地层压力的衰竭、边底水的锥进,气体流速逐渐降低,当气体流速不足以携带井筒中的液体时,井筒开始积液,气井一旦积液,将严重影响气井的正常生产,甚至出现水淹停喷的现象。因此,准确预测气井积液时机对于气井的高效开采至关重要[1]。苏里格区块属于典型的低渗致密气藏,且气藏水体分布复杂,目前苏里格区块定向井占比高达15%,其中苏20、苏25、苏49 和苏76 区块已积液气井占比达到21%,严重制约了气井的正常生产,大幅降低气井产能。因此,准确预测气井积液时机对提高苏里格区块气井产量至关重要。常见的TURNER 等[2-4]液滴模型并不适用于苏里格区块定向井(现场定向井井斜角低于45°,主要集中在30°左右),现场试验结果表明,常用的液滴模型预测结果偏低,误差较大,主要是由于角度的存在使得液滴无法在管道中长距离运移,最终液滴会撞击管壁形成液膜。表1为不同携液模型考虑因素汇总,李闽等[5-14]对液滴形状、曳力系数、安全系数以及模型系数进行了修正。1969年,WALLIS等[15]提出了液膜反转是气井积液的主要原因,之后BELFROID 等[16-18]开展了倾斜管气井携液机理研究,在TURNER 模型基础上添加了角度修正项从而建立了适用于水平井的临界携液模型,但该模型仍然是液滴模型的延伸,未考虑液体流量(Ql)对临界携液流速的影响,与实验观察相悖。虽然BARNEA 提出了较为完善的机理模型,但由于机理模型计算复杂、需要的条件苛刻,导致其适用性较差[19]。为建立适用于定向井的临界携液模型,开展了不同管径、液体流速、气体流速、角度条件下气井积液与携液测量实验。

表1 不同携液模型考虑因素汇总Table 1 Summary of factors to consider in different liquid-carrying models
1 实验装置及参数范围
1.1 实验系统
为研究定向井积液与携液机理,设计并搭建了实验装置。图1为实验流程,由供液系统、供气系统、测控系统和实验架组成,其中实验架包括有机玻璃管、标尺、2 个压力传感器、实验支架等,实验支架可实现任意角度条件。供气系统包括螺杆式空压机、储气罐、气体流量计、压力计等。供液系统包括水箱、液体泵、液体流量计。实验测控系统包括无纸记录仪、电脑,其中无纸记录仪可同步计量液体流量、气体流量(Qg)、压力数据,实现数据的实时同步测控,保证了实验的准确度,同时配备有高速照相机,可实时拍摄管道中液体流动状态。

图1 定向井积液与携液流动模拟实验流程Fig.1 Flow chart of simulation experiment for liquid loading and carrying flow in directional wells
1.2 实验范围
实验管道采用是内径为50、62、76 mm 的有机玻璃管,总长度7 m,为消除入口效应的影响,压力计和照相机流动规律拍摄点离入口距离2 m,实验介质为空气和水,气体流量介于0.1~300.0 m3/h,液体流量介于0.1~20.0 m3/h,压力介于0~0.8 MPa,温度为室温,角度介于5°~30°(根据苏20、苏25 和苏76 区块的46 口定向井数据获得见图2),为方便观察倾斜管中积液与携液规律,选用的是透明的有机玻璃管,且贴有刻度。为了准确计量气体流量,在气体流量计后,安装了压力传感器10,其主要目的是用来折算实验管道中气相流速,高速照相机可拍摄倾斜管气液两相流动规律。
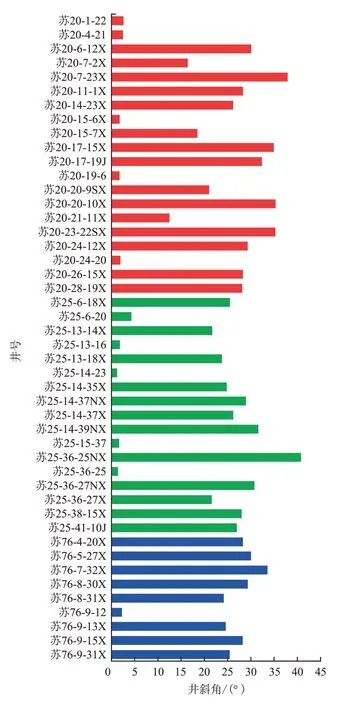
图2 苏20、苏25和苏76区块定向井井斜角范围Fig.2 Inclination range of directional wells in Block Su20,Block Su25 and Block Su76
2 实验现象及结果
2.1 气体流量对积液的影响规律分析
本次实验重点研究倾斜管中气井积液与携液流动规律。因此,分别进行了15°、30°、45°时气井积液与携液流动规律测量实验研究,图3 是倾斜角为15°时(与垂直法线方向夹角),不同气量条件气液流动规律,本次实验中观察到,当液体流量较低时(0.2 m3/h),气量为180 m3/h时,液体以液膜或液滴的形式在管道中连续向上流动,在高气量条件下液体主要以液膜和液滴的形式流动,这主要是由于气体流量较大时,气体对液体剪切力较大,管壁上的液膜会被撕碎成液滴,由于倾斜管中角度的存在,导致液滴无法长距离运移,最后会撞击在管壁上形成液膜,这与FADILI观察的现象一致[20]。随着气体流量的降低(170 m3/h),气体对液体的剪切力逐渐减小,导致液滴量在逐渐减少,当气体流量进一步降低(120 m3/h),气体剪切力不足以携带液体时,液膜开始反转,此时管道下部逐渐出现液膜聚集现象见图3d。图4 和图5 分别是角度30°和45°时积液过程,与15°时表现规律一致。

图3 倾斜角为15°时积液过程Fig.3 Liquid loading process at 15°

图4 倾斜角为30°时积液过程Fig.4 Liquid loading process at 30°
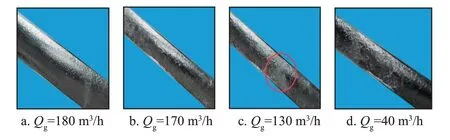
图5 倾斜角为45°时液积液过程Fig.5 Liquid loading process at 45°
图6为气相表观流速与压力梯度关系曲线,可知随着气相表观流速的减少,压力梯度逐渐减小,当气体流速低于9 m/s 后出现压力梯度快速增加的现象,这主要由于在高气体表观流速条件下,气体摩擦阻力梯度占据主导作用,随着气体流速的降低,液体重力作用逐渐增强。当气体对液体剪切力不足以携带管壁上液膜时,液膜开始出现回落现象,液膜回落瞬间液体与管壁间的摩擦阻力趋于0,由于此时液体整体趋势仍然向上运移,所以摩擦阻力仍然存在。图7为不同气体流量条件下压力梯度变化曲线,可知随着气体流量的减小,压力梯度逐渐增大,且压力梯度波动幅度在逐渐增大。

图6 气相表观流速与压力梯度关系曲线Fig.6 Gas superficial velocity and pressure gradient relationship curves
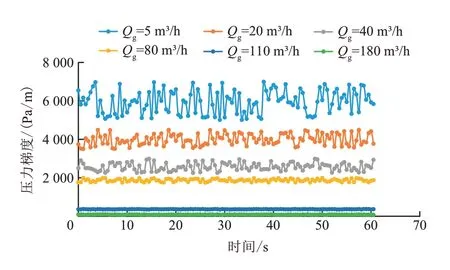
图7 不同气体流量条件下压力梯度变化曲线Fig.7 Pressure gradient variation curves under different gas flow rate
2.2 角度变化对积液影响规律分析
从图3b、图4b、图5b 可以看出,在相同条件下,随着倾斜角度的增大,管壁上液膜厚度的分布均匀度降低,这主要是由于随着角度的增加,重力作用逐渐增强,靠近管壁下部的液膜厚度逐渐增加。从图3c、图4c、图5c可知,随着倾斜角度的增加,管壁下部液膜厚度逐渐增大,液膜开始发生反转时所需的气体流量逐渐增大,临界携液气量逐渐增加。图8为不同角度条件下的压力梯度变化曲线(Ql=0.2 m3/h,Qg=150 m3/h),可知随着角度的增大,压力梯度逐渐减小,同时波动幅降低。图9为不同角度条件下临界携液流速,可知随着倾斜角度的增加,临界携液流速逐渐增大,这主要是由于随着角度增加管道下部液膜厚度逐渐增大,携带液体需要更大的临界携液流速。
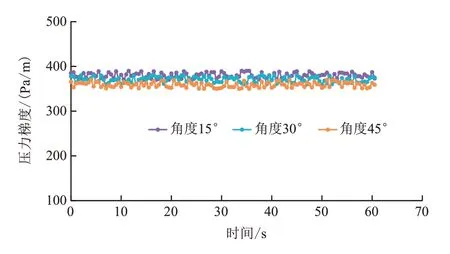
图8 不同角度条件下压力梯度变化曲线Fig.8 Pressure gradient variation curve under different angle
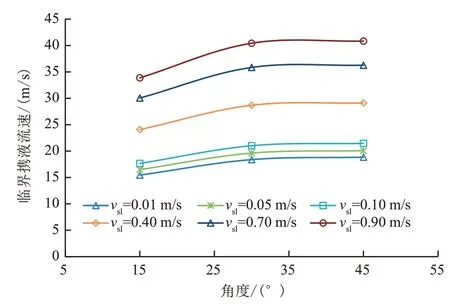
图9 角度与临界携液流速关系曲线Fig.9 Relationship curves between angle and critical liquid carrying flow rate
2.3 液体流量对积液影响规律分析
对于倾斜管来讲,液滴模型已不再适用,BELFROID 在TURNER 模型基础上添加角度项进行修正,但BELFROID 认为液膜反转才是倾斜管积液的根本原因。无论是TURNER 模型、SHI 模型还是BELFROID 模型,在建立临界携液模型时都忽略了液体流量对临界携液流速的影响,但从DUNS 等[21]提出的过渡流与环状流转换边界来看,液体流量直接会影响气井积液过程。为研究液体流量对气井积液的影响,分别分析了不同液量条件下临界携液流速。图10 为角度45°、气体流量180 m3/h 条件下不同液体流量时携液情况,可知当液体流量较低时(小于0.2 m3/h),此时管道中呈现出高速流动的环状流,液体以液膜的形式连续向上携带,当液体流量大于0.6 m3/h 后,管道出现了液膜反转和堆积的现象,随着液量的增加,管道中液体回落的幅度越来越大,过渡流的流动特征越来越明显,积液现象越来越严重,这表明液体流量是影响气井积液的重要因素,在模型建立时不能被忽略,这与WANG等[12]的观点一致。

图10 不同液体流量条件下携液状态Fig.10 Liquid carrying state under different liquid flow conditions
图11 为液体流量0.1、0.2、0.6、1.0、1.5 m3/h 时的压力梯度变化曲线,可知气体能正常携液时管道压差波动较小,随着液量的增加管道中压力梯度逐渐增大,压力梯度波动幅度逐渐增大,气液流动越来越呈现出过渡流的流动形态和特征,井筒严重积液。

图11 不同液体流量条件下压力梯度变化曲线Fig.11 Pressure gradient variation curves under different liquid flow rate conditions
图12为液体表观流速与临界携液流速的关系曲线,可知随着液量的增大,临界携液流速逐渐增加,而常规的液滴模型忽略了液体流速对临界携液流速的影响,明显不合理。

图12 液体流速与临界携液流速关系曲线Fig.12 Relationship curves between liquid flow rate and critical liquid carrying flow rate
2.4 管径对临界携液流速的影响
油管尺寸是影响气井积液的另外一个因素,因此,本次实验同样分析了管径对临界携液流速的影响规律,图13为管径对临界携液流速的影响规律,可知随着管径的增加,临界携液流速在逐渐增大,这主要是由于在环状流条件下,随着管径的增加液膜量逐渐增大,携带液体需要更大的气量。

图13 管径与临界携液流速变化曲线Fig.13 Variation curves of pipe diameter and critical liquid carrying flow rate
图14 为不同油管尺寸条件下气水两相流动状态,可以看出在气体流量130 m3/h,液体流量0.2 m3/h,油管内径分别为50、62、76 mm 时的流动状态,可知当油管内径为50 mm 时,气体可以连续携带液体,随着管径的增加,气体携带液体能力逐渐减弱,这主要是由于管径越大,气体流速越小,需要的临界携液流速越大。从图14c可知当油管内径为76 mm 时,管道下部出现了液体的聚集,已经呈现出分层流的迹象,同时液体液开始发生回落情况,因此,管径越大临界携液流速越大。

图14 不同油管尺寸条件下流动状态Fig.14 Flow state under different tubing sizes
3 临界携液模型建立
3.1 模型建立
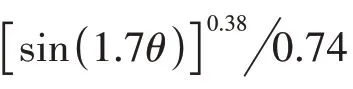
式(1)中:vsg为临界携液流速,单位m/s;C是经验常数。
在垂直管中,1969年WALLIS等[15]提出了无因次气流可作为液膜反转的判断准则,并提出了经典的液膜反转界限方程(经验方程):
上述方程可转化为:
式(2)—式(3)中:D为油管内径,单位m。

式中:a1、a2为系数。
利用实验数据对C值进行分析发现,C值是关于液相表观流速、管径的函数,随着液相表观流速和管径的增大C值逐渐增大,m是关于油管尺寸的线性函数,随着管径的增大m逐渐增大(图15)。本次实验中C值介于0.85~1.80,m值介于0.34~0.49。
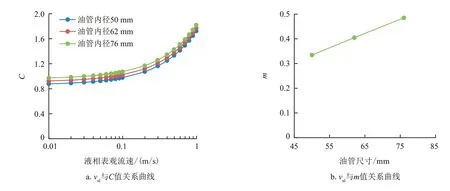
图15 vsl与C值和m值关系曲线Fig.15 Relationship curves of vsl and C,m,respectively
基于实验数据,分别对C和m进行拟合可得到C和m的函数方程:
将式(5)和式(6)带入到方程(4)中可拟合得到a1和a2值:
将式(5)、式(6)和式(7)代入到式(4)中,即可得到定向井临界携液模型:
图16 为模型计算值与实验测量值的对比图,可知计算值与实测值均匀地分布在对角线上,表明新模型计算精度较高,平均相对误差为-0.38%,平均绝对误差为4.29%。

图16 模型计算值与实验测量值对比Fig.16 Comparison of model calculated values with experimental measured values
3.2 模型验证
为了进一步验证本模型的准确性,收集整理VEEKEN[23]文献中62 口积液气井数据,角度范围介于13°~64°、产液量介于0.012~6.280 m3/d,油压介于0.4~11.1 MPa,管径介于44.704~156.972 mm,天然气密度介于0.58~40.00 kg/m3,同时利用文献数据分别与BELFROID 模型、李丽模型、刘永辉模型、WANG 模型、TURNER 模型等进行了比较,图17为新模型与VEEKEN 文献数据对比结果,可知新模型在预测62 口气井时,有57 口气井判断积液,准确率为91.94%,进一步表明新模型的准确度较高。
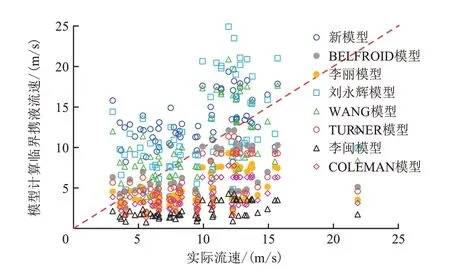
图17 新模型与VEEKEN文献数据对比结果Fig.17 Comparison results between the new model and VEEKEN literature data
4 结论
1)定向井积液规律实验结果表明:在相同角度、液量条件下,管径越大,临界携液流速越高;随着角度的增加,管壁下部液膜厚度逐渐增大,井筒越容易产生积液;液体流速越大,临界携液流速越大,因此,不能忽略液体流速对临界携液流速的影响;液滴模型不适用于倾斜管,液膜反转是引起倾斜管积液的主要原因。
2)基于BELFROID 模型和WALLIS 提出的液膜反转经验模型,考虑管径、气体密度、液体密度、角度、液体表观流速、重力加速度等参数,建立了定向井临界携液模型,并基于实验数据得到了C和m值的表达式,在预测实验值时新模型的平均绝对误差为4.29%,在预测文献中62口积液气井时新模型预测准确度为91.94%,计算精度较高,同时新模型较常规模型考虑了液体流速和管径的影响,适用性更强。
3)本模型仅适用于井斜角低于45°、油管尺寸介于50~76 mm 的定向井,并不适用于预测角度大于45°的气井。
