基于改进蚁群优化算法的AGV路径规划

陈岁繁,王浈元,李其朋

(浙江科技大学 机械与能源工程学院,杭州 310023)

路径规划是移动机器人(automatic guided vehicle,AGV)实现自主移动与导航功能中必不可少的一部分[1-2]。传统的优化算法主要有经典算法和智能算法。经典算法有A*算法[4]、快速随机树(rapid random tree,RRT)算法[5]等,智能算法包括遗传算法[6]、粒子群算法[7]、蚁群算法[8]等。蚁群算法由于鲁棒性强,且易与其他算法结合,成为研究热点。但是蚁群算法也存在搜索空间大、局部最优、收敛速度慢、拐点较多等问题。研究者基于蚁群算法缺点,提出了很多改进方案。例如:刘新宇等[9]提出一种蚁群-聚类自适应路径规划方法,解决了传统蚁群收敛速度慢的问题;宋宇等[10]通过结合A*算法,对启发函数、信息素浓度及挥发因子进行重新定义,提高了算法的寻优能力和搜索效率。Masoumi等[11]设计了一种以用户为多目标中心的蚁群优化算法,能适应不同优先级的多目标优化问题;高茂源等[12]分别从启发因子、信息素及挥发因子三个方向改进蚁群算法,提升了算法的收敛速度和寻优效率。

基于传统蚁群算法在AGV路径规划中有搜索效率低、寻找路径长、拐点个数多等方面的问题,本研究设计了一种改进的蚁群优化算法。首先对启发函数进行改进,提升搜索效率;然后更新信息素,解决路径规划时易陷入局部最优的问题;接着降低路径的拐点;最后引入动态避障策略,解决路径规划时出现的死锁。

1 环境模型构建

1.1 栅格图

环境模型有很多,比如可视图空间、拓扑图、栅格地图等。栅格地图是运用黑白两色栅格表示AGV的可移动区域和禁行区域[13-14],对障碍物的表示简单易懂,是目前环境建模中应用较多的模型。以10×10栅格为例,建立静态环境下AGV运动栅格地图,如图1所示。

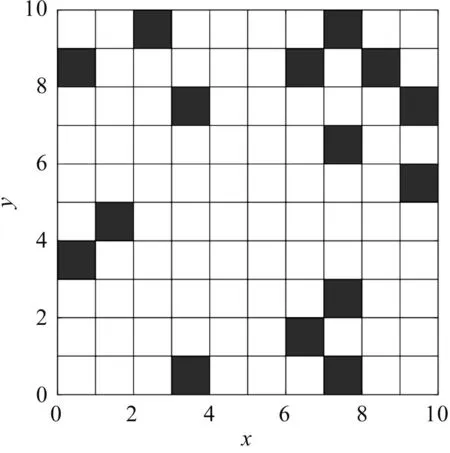
图1 栅格地图Fig.1 Grid map

根据环境模型,设置栅格地图的栅格号从下往上、从左往右依次按1、2…10的顺序递增,坐标(xi,yi)(i为栅格号)与栅格编号的关系如下:

(1)

式(1)中:L为栅格边长;X为栅格地图行数;Y为栅格地图列数。

1.2 步长搜索方式

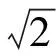
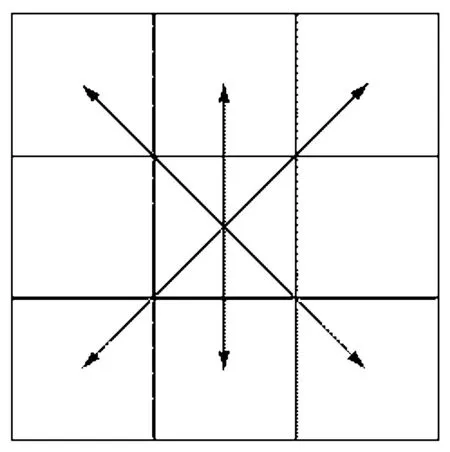
图2 步长搜索方式Fig.2 Step size search method

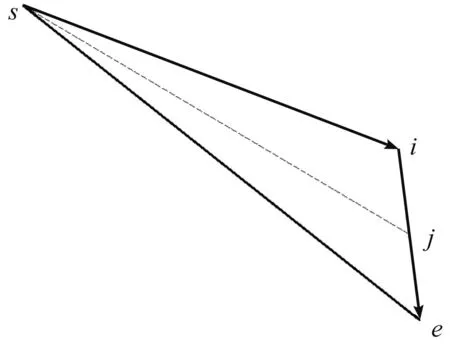
图3 路径的各个节点Fig.3 Each node of the path

2 蚁群算法

蚁群算法是20世纪末科学家Dorigo等最早提出的一种智能算法[16],该过程包括状态概率(state transition probability,STP)的选择和信息素的更新(pheromone update,PU)。

2.1 状态概率选择

传统蚁群算法在搜索过程中根据蚂蚁当前栅格和障碍物选择下一可行栅格,蚂蚁t时刻从节点i运动到节点j的概率一般通过轮盘赌法确定,它的状态转移概率

(2)

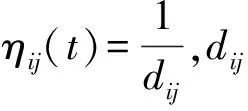
2.2 信息素更新

信息素更新包括信息素挥发和强化。信息素挥发,一是防止信息素浓度过高掩盖启发信息,二是避免过快陷入局部最优。信息素强化是为了让蚂蚁向最优解靠近,增加经过路径上的信息素浓度,加快路径最优解的寻找速度。信息素更新表达式如下:

τij(t+1)=(1-ρ)τij(t)+Δτij(t) 。

(3)

(4)

式(3)和式(4)中:(1-ρ)为信息素残留;Δτij(t)为t时刻蚂蚁从路径坐标(i,j)中经过时的信息素增量;Q为信息素强化系数;Lk为蚂蚁k从起始点到目标点之间的路径总长。

3 改进的蚁群算法

3.1 改进的启发信息

传统蚁群算法只考虑了蚂蚁t时刻在路径坐标(i,j)上的距离,本研究引入起始点和目标点,路径的各个节点如图4所示。

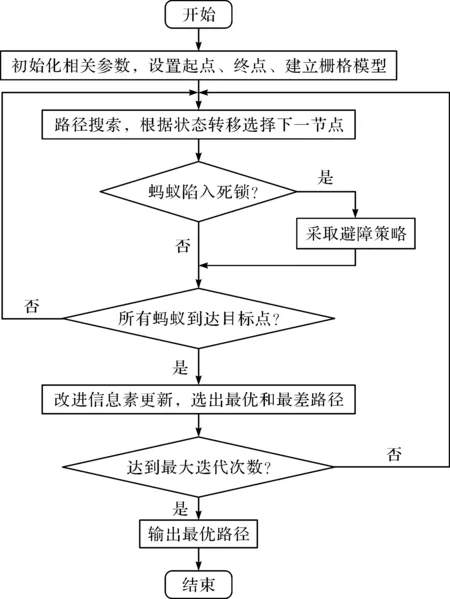
图4 改进的蚁群优化算法流程图Fig.4 Flowchart of improved ant colony optimal algorithm

预估代价最早出现在A*算法中,它指当前点到目标点之间的大概距离,而不是精确数值,可以引导算法朝着最短目标路径方向去搜索。预估代价的计算一般采用曼哈顿距离[17],即两点在水平方向上的总和。

成熟收获前对所有试验小区均取样考种，共36个小区，每处理10株进行考种。考查性状有株高、根颈粗、有效分枝部位、主花序长、单株一次和二次分枝数、单株角果数、角粒数、千粒重、单株产量。实收小区产量晒干折单产。

在引入预估代价值的基础上,添加一个平衡因子,加快算法的收敛。综合考虑起始点、当前点、下一点、目标点,使蚂蚁搜索空间变小,搜索效率得到提升,增强路径寻优能力。改进后的表达式如下:

(5)

(6)

式(5)和式(6)中:dje为节点j到目标点e的距离;ε为平衡因子;dsi为起始点s到节点i的距离;Nc和Nm为迭代次数。

3.2 改进的信息素更新

对信息素的更新主要围绕着路径来进行。

3.2.1 狼群分配机制

传统的蚁群算法在对最优和最差路径中的信息素进行更新时,由于所用方法相同,路径中的信息素相差不是很大,路径的搜索效率也有所下降。因此,需要对信息素的更新公式进行改进,在此引入狼群算法。狼群在捕猎时主要有搜索、围攻、更新几种行为,狼群算法是受狼群捕猎时的行为启发提出的一种算法[18]。头狼最具智慧和攻击性;探狼是狼群的精锐,需要探找猎物;其余需要围攻猎物的狼称为猛狼。狼群捕猎的基本过程包括游走、奔袭、召唤、狼群更新等[19]。

寻找到最差路径的蚂蚁,会散发信息素,这样会诱导在后面的搜寻路径的蚂蚁。采用狼群分配机制,可以防止路径陷入局部最优,有效缩短蚂蚁搜索路径的长度。改进的信息素更新表达式如下:

τ′ij(t+1)=τij(t+1)+Δτij,2-Δτij,1;

(7)

(8)

(9)

式(7)、式(8)和式(9)中:Δτij,1、Δτij,2分别为最差路径信息素减少量和最优路径信息素增加量;ξ和λ分别为每次搜索时找到的最优、最差蚂蚁数;L1和L2分别为蚂蚁到达目标点的最长、最短路径;Lav为蚂蚁到达目标点的平均路径;Q1和Q2分别为信息素的减少和增加系数,取Q1=0.5,Q2=1。

3.2.2 拐点影响因子

传统蚁群算法在更新信息素时,一般只考虑路径长度,而没有考虑路径拐点带来的影响。因此,本研究对信息素增量Δτij(t)进行改进,加入拐点影响因子,动态调节路径长度和拐点的数目。改进后的表达式如下:

(10)

Sk(t)=xLk+yFk。

(11)

式(11)中:x为路径长度因子;Lk为路径的总长;y为拐点影响因子;Fk为拐点个数;x和y的取值范围均为(0,1]。

3.3 动态避障策略

蚁群在最初搜索时,会产生许多交叉路径,由于禁忌表的存在,很多蚂蚁没有到终点,就在最后搜索的路径上停下来,于是就会发生死锁[20]。遇到复杂环境时,出现死锁的概率更高,从而降低了收敛速度。传统回退策略虽然可以减少死锁蚂蚁,但回退次数过多会使搜索时间变长,影响搜索效率。对此,本研究引入改进的避障策略,在蚂蚁搜索初期,加入动态避障因子Tj,得到新的状态概率表达式如下:

(12)

(13)

式(12)和式(13)中:σ为避障系数,取值为大于0的常数;G1为表示节点j周围可行栅格;G2为障碍栅格;G3为被禁忌表限制栅格。

3.4 改进的蚁群优化算法流程

改进的蚁群优化算法流程图见图4。

4 仿真试验分析

仿真平台,MatLabR2017a软件;仿真环境,系统为Windows 10,64 bit,内存为8 GB,CPU为core i5-82501,6 GHz。

4.1 参数分析

每个参数在各自合适的范围内各选取5个值,组成相应集合:ρ∈{0.1,0.3,0.5,0.7,0.9};Q∈{1,5,8,10,12};α∈{1,2,3,4,5};β∈{1,3,5,6,8};根据参数集合,选取一组初始参数:α=1,β=1,ρ=0.1,Q=1;设置蚂蚁数M=50,迭代次数N=100;仿真试验在20×20的栅格环境下进行,每次只改变其中一个参数值。首先改变启发因子α,分别仿真试验5次,选择得到最优路径和最小迭代次数的数值,之后依此类推;将每个参数仿真所得到的数据拟合,各参数对路径长度和迭代次数的影响见图5。由图5可知,上述4个参数可以取得最佳路径和最小迭代次数的数值范围分别为2≤α≤3、5≤β≤6、0.5≤ρ≤0.7和8≤Q≤10。根据各参数范围可以选出最佳参数,见表1。

表1 最佳参数Table 1 Best parameter

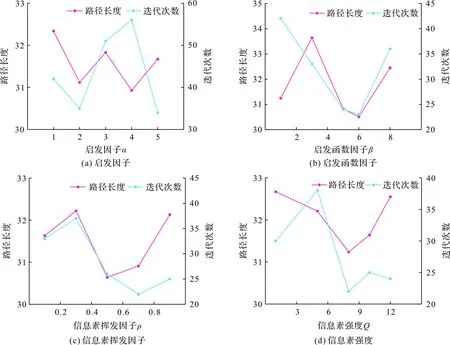
图5 各参数对路径长度和迭代次数的影响Fig.5 Impact of various parameters on path length and iteration times

4.2 20×20栅格环境的试验

选择简单的栅格环境进行仿真,将本研究改进的蚁群优化算法所得结果分别与传统蚁群算法、高茂源等[12]的算法进行对比,在20×20栅格环境下的仿真数据见表2,3种蚁群算法的路径和收敛情况如图6所示。

表2 3种蚁群算法在20×20栅格环境下的仿真数据Table 2 Simulation data of three ant colony algorithms under grid environment 20 × 20

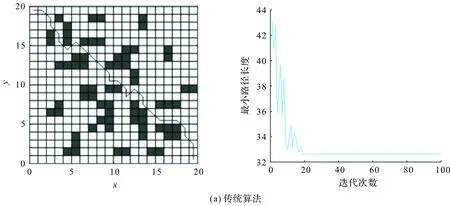
图6 3种蚁群算法在20×20栅格环境下的路径和收敛情况Fig.6 Path and convergence of three ant colony algorithms under grid environment 20 × 20

由表2可知,在简单栅格环境下,运用本研究的改进的蚁群优化算法,得到的最佳路径长度、迭代次数及拐点数,相比传统蚁群算法分别降低了9.7%、57.8%、65.0%,相比高茂源等[12]的算法,分别降低了4.3%、38.5%、46.2%。

4.3 30×30栅格环境下试验

为了更加深入地验证改进的蚁群优化算法具有先进性,再选择复杂的栅格环境进行仿真,在30×30栅格环境下的仿真数据及3种蚁群算法的路径和收敛情况,见表3及图7。

表3 3种蚁群算法在30×30栅格环境下的仿真数据Table 3 Simulation data of three ant colony algorithms under grid environment 30 × 30

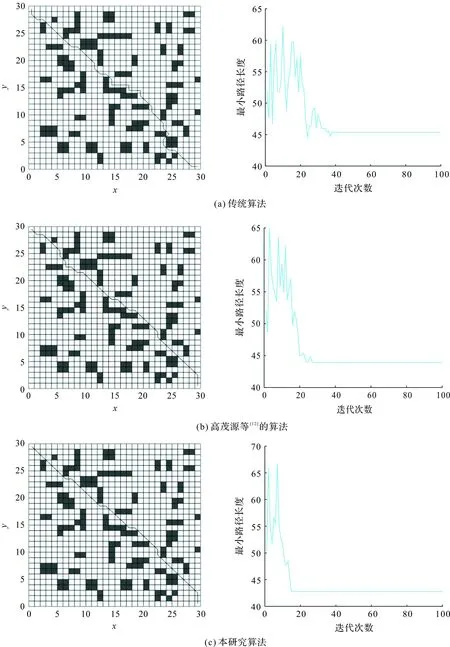
图7 3种蚁群算法在30×30栅格环境下的路径和收敛情况Fig.7 Path and convergence of three ant colony algorithms under grid environment 30 × 30

由表3可知,在复杂栅格环境下,相比传统蚁群算法及高茂源等[12]的算法,运用本研究的改进的蚁群优化算法,最佳路径长度分别缩短了6.6%、3.6%,拐点数分别减少了64.0%、43.7%,迭代次数分别降低了60.5%、42.3%。

通过在简单环境及复杂环境下进行仿真可以看出,本研究的改进的蚁群优化算法在搜索效率、收敛速度、路径寻优等方面,相比传统蚁群算法及高茂源等[12]的算法有了较大的提高,提升了AGV路径规划的综合性能。

5 结 语

传统的蚁群算法在AGV路径规划时存在搜索效率低、拐点个数多、寻找路径长等问题。本研究设计了一种改进的蚁群优化算法:首先,在蚁群优化算法中加入预估代价值策略来改进启发函数,不仅增强了目标点向导作用,而且提升了搜索效率;然后,更新信息素,通过结合狼群算法分配机制,解决路径规划时易陷入的局部最优问题;接着,降低路径的拐点;最后,引入动态避障策略来解决死锁。仿真试验表明,相比传统算法,AGV运用改进的ACO算法进行路径规划,迭代次数和拐点数等均有显著降低,证明改进的ACO算法提升了AGV路径规划的性能,可以很好地解决AGV路径规划时遇到的问题。