基于载波调制PWM的对称六相与三相PMSM串联系统矢量解耦控制

刘陵顺，闫红广，葛宝川

（海军航空大学，山东 烟台 264001）

0 引言

近年来，多相电机因其具有高效率、小力矩脉动、低噪声、强容错性以及低逆变器电压或电流值等优点，在舰船电力驱动、多电飞机、机车牵引、电动汽车等领域得到越来越多的关注[1-3]。此外，高于五相的多相电机，还可以实现同一逆变器（Voltage Source Inverter，VSI）驱动的多台电机串联系统的独立运行[4-7]。这是因为每台多相电机的矢量控制只需要2个电流分量，多余的自由度可用于完成控制与其串联的其他电机。这种多电机运行模式经济性强、节省空间，因而在武器装备、纺织、造纸等行业具有潜在应用价值。

在多电机串联系统中，电机各相绕组之间需要遵循一定的串联联结关系。文献[8-9]对奇数相和偶数相多相电机的串联规则进行了系统研究。文献[9]介绍了2 台五相感应电机的串联系统，相对于定子绕组之间的直接联结，按照特定的串联规则更有助于提高直流母线电压的利用率。文献[10-12]指出，串联系统中各电机独立运行的理论基础是要求每台电机具有正弦波分布的磁动势。

在对称六相与三相电机的串联驱动系统中，用于控制六相电机的电流分量不流过三相电机，而当三相电机功率远小于六相电机功率时，控制三相电机的电流分量在流过六相电机时产生的影响可以忽略，因而更适用于大功率六相电机串联小功率三相电机的应用场合。针对这种串联系统的共直流母线结构特点，文献[13]指出，要合理分配母线电压以提高母线电压利用率，同时进行电流限制以保证逆变器可靠工作。

对于这种新颖的单逆变器多电机串联解耦控制技术，国外的研究主要集中在多相感应电机构成的串联系统方面。文献[14-16]研究了隐极式对称六相和三相PMSM 串联系统中，对于非正弦磁动势中的空间谐波耦合规律及解耦控制策略，并基于仿真验证指出永磁同步电机同样可以构成这种串联系统。文献[17-18]研究了凸极式对称六相和三相PMSM 串联系统的控制问题，实现了2 台电机控制量的分别给定和解耦运行。

针对凸极式对称六相与三相PMSM 构成的串联系统，基于其解耦控制的数学模型，本文分析了电压补偿方法、控制量变换与叠加方法、电流限制方法、直流母线电压的分配方法等。设计了零序信号注入的载波调制PWM 控制策略，试验验证了变速、变负载等不同运行工况下动态解耦运行的可行性。

1 基于载波调制PWM的矢量控制系统

在单逆变器驱动的对称六相与三相PMSM串联系统中，2台电机定子绕组的连接方式如图1所示[10]。

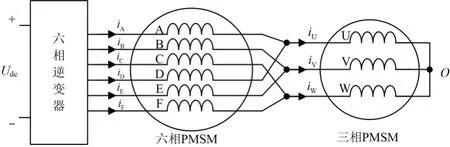
图1 对称六相串联三相PMSM系统示意图Fig.1 Symmetrical six-phase series-connected three-phase PMSM system

六相（VSI）的六路输出分别对应连接至对称六相PMSM 的绕组引入端，六相电机A 相和D 相绕组的引出端连接在一起，并接至三相电机的U 相引入端；同理，可完成BE-V、CF-W 相绕组的连接。经理论分析可知，六相VSI输出电流经过解耦变换后，分别映射到d1q1、d2q2和o1o2这3个相互垂直的子空间中。可利用d1q1子空间内的电流分量实现对称六相PMSM 的独立控制；利用d2q2子空间内的电流分量实现三相PMSM 的独立控制；o1o2平面为零序平面，仅产生损耗，不参与任意一台电机的机电能量转换。这样即可实现对称六相和三相PMSM 系统在同一台VSI 驱动下的解耦控制[18]。

1.1 串联系统的数学模型

串联系统在自然坐标系下的定子电压方程为：

式（1）中：ΨsA～ΨsF、ΨsU～ΨsW分别为对称六相和三相PMSM 每相定子绕组磁链；rs1、rs2分别为对称六相和三相PMSM 每相定子绕组电阻；iA～iF和iU～iW分别为对称六相和三相PMSM每相绕组电流。

式（3）（4）中：θr1与θr2分别为2 台电机转子磁场轴线与定子A相或U相绕组轴线之间的电角度。

对称六相与三相PMSM 在d1q1、d2q2坐标系下的电压、磁链分别为：

式（5）～（8）中：Ld1、Lq1、Ld2、Lq2、Lsσ1、Lsσ2分别为对称六相和三相PMSM 在d1q1、d2q2坐标系下的主电感和定子漏感；ωr1、ωr2、ψf11、ψf21分别为对称六相和三相PMSM的转速、转子永磁磁链。

由式（7）（8）可知，在这种串联系统中：三相PMSM 对六相PMSM 没有任何影响；而六相PMSM 要在三相PMSM 产生1 个漏磁压降，但是这并不影响两者的解耦和独立控制。

对称六相PMSM的转矩方程为：

式（9）（10）中：p1和p2分别为六相和三相PMSM 的极对数。

对称六相和三相PMSM 的电磁转矩分别由id1、iq1和id2、iq2控制。id1、iq1和id2、iq2分别处于2 个相互正交的子空间内，因此，可分别实现独立控制2台电机。

1.2 电压补偿以及电压给定值的叠加方法

根据串联规则，可得VSI调制信号给定电压如下：

三相PMSM 的磁通/力矩电流分量需要流经六相PMSM，所以六相PMSM 的定子漏阻抗将在三相PMSM 上产生压降。在生成VSI 控制信号时，漏阻抗压降的耦合作用需要进行补偿。其中，对称六相PMSM的ed1、eq1表达式如下：

三相PMSM的ed2、eq2表达式如下：

由式（12）可以看出，对称六相PMSM 的ed1、eq1表达式不包含三相PMSM 的漏阻抗引起的压降，这主要是因为对称六相PMSM 的磁通/力矩电流分量流经三相PMSM 时，在串联联结点处相互抵消，因而不会在三相PMSM 上产生漏阻抗压降。式（13）中的漏阻抗压降系数设置为0.5，主要是因为三相PMSM 相电流的一半流经六相PMSM的每一相中去。

综上所述，在该控制策略下，控制对称六相PMSM的电压给定值为：

控制三相PMSM的电压给定值为：

将对称六相PMSM 调节并补偿后产生的电压给定值ud1、uq1以及三相PMSM 调节并补偿后产生的电压给定值ud2、uq2分别进行的坐标反变换后，形成各自的uα、uβ和uz1、uz2；再对其分别完成2 6 变换和2 3 变换，形成控制对称六相PMSM 电压给定值u*A～u*F以及控制三相PMSM 的电压给定值u*U～u*W；最后，按照式（11）对应叠加及限制后得到六相VSI 的控制电压信号，为载波调制PWM提供调制波。

1.3 电流限制策略

由于2 台电机工作所需电压和电流均由VSI 提供，VSI 能够提供给所带负载的电流上限取决于开关器件的自身性能以及采取的制冷方式[18]，在id=0的矢量控制策略下，该串联系统中电流限制表达为：

式（16）中：IM表示逆变器输出相电流最大幅值，表示逆变器输出相最大有效值。

每台PMSM的限制电流值为：

1.4 直流母线电压的分配关系及提高方法

为了控制2 台串联PMSM 的独立运行，应用载波调制PWM技术须要形成2个频率信号的叠加信号，使逆变器输出2个正交子空间内各不关联的电压信号驱动各自的PMSM。另外，采用改进的载波调制PWM技术，即利用零序信号注进后的载波PWM 方法提高线性控制区域，如图2所示。

图2 零序信号注入调制的载波Fig.2 Carried-wave modulated with zero-sequence signal injection

由于2 台PMSM 串联在同一台VSI 中，VSI 线电压则取决于2台PMSM的线电压叠加。考虑到它们的电压给定值的频率、最大值以及相位关系在大多数情况下均不同，在线性调制范围内必须使VSI 的2 个线电压同时达到极值作为可行范围，即可行范围内的任一工作点均能实现线性调制，工作点的实际位置取决于它们的转速和负载大小[9]。

定义调制度：

式（19）中：V1为相电压基波最大值；Udc为直流母线电压；i=1,2分别表示六相和三相电机。

在线性调制范围内，可得：

2 台电机调制度MM1、MM2的线性可行范围如图3所示。

图3 对称六相串联三相PMSM系统线性调制范围Fig.3 Linear modulation region of two-motor series-connected system

六相电机的给定相电压是由调制度MM1和直流母线电压Udc以及角频率ωr1决定的；而三相电机的给定电压表达式是由调制度MM2和直流母线电压Udc以及角频率ωr2决定的。

需要注入的零序信号Zs设定为：

其在-Udc2-uMIN≤Zs≤Udc2-uMAX范围内。

式（21）中：

将零序信号Zs与原调制信号简单相加后，得到如下方程组，该方程组表征调整后的合成调制信号：

定义调制信号的最大值为：

定义调制信号的最小值为：

经推导可得：

调整前的合成调制信号相对于坐标横轴来说是上下不对称的，这样很容易超出线性调制范围，即超出载波幅值范围，产生过调制问题。经调整后，合成的调制波信号相对于坐标横轴是上下对称的，实现了线性调制范围扩大和直流母线电压利用率的提高。

1.5 串联系统基于载波调制PWM的矢量控制系统

图4 给出了基于载波PWM 调制的id=0 矢量控制系统框图。图中有2 个反馈量：一路是六相VSI 的输出电流，该电流经变换矩阵T计算后得到αβ子空间和z1z2子空间的电流值，然后经各自同步旋转坐标变换矩阵R1和R2，得到电流分量实际值，即将对称六相PMSM 的αβ子 空 间 的iα、iβ转 变 成id1、iq1，将 三 相PMSM 的iz1、iz2转 换 成id2、iq2，最 后 将id1、iq1和id2、iq2反馈到系统输入端与给定值进行比较产生控制信号；另外一路是2台电机的转子位置角，该参数起到两个作用，一是提供转角信号给控制系统各个坐标变换使用，二是该信号经微分后反馈到比较器输入端与给定转速进行比较，实现转速的稳定和控制。

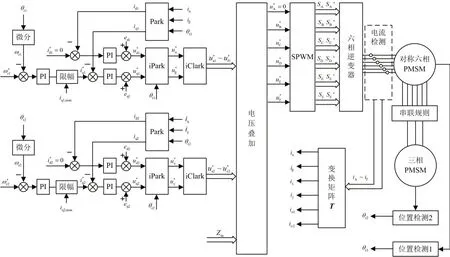
图4 基于载波调制PWM的id=0矢量控制系统原理图Fig.4 Schematic diagram of vector control system of id=0 based on carried-wave modulated PWM

2 系统试验

对称六相永磁同步电动机及其串联三相永磁同步电动机的样机，六相PMSM参数：额定功率P1=1.5kW，额 定 转 速n1=1500r/min，p1=2，rs1=1Ω，Ld1=0.003mH，Lq1=0.0057mH，ψf1=0.2Wb。 三 相PMSM 参数：额定功率P2=1.5kW，额定转速n2=1500r/min，p2=2，rs2=1.2Ω，Ld2=0.01mH，Lq2=0.02mH，ψf2=0.45Wb。在串联系统稳态运行（六相电机转速为500 r/min、负载转矩为2.7 N·m；三相电机转速200 r/min、负载转矩2 N·m）的基础上，分别进行单台电机负载、转速的突变试验。

2.1 六相PMSM负载和转矩突变的动态试验

现将六相电机转速给定，由500 r/min 突变为600 r/min，待稳定后再突变为500 r/min。观察2 台电机的实际转速和转矩变化，结果如图5 a）所示；将六相电机的负载给定，由2.7 N·m 突变为0 N·m，待稳定后再突变为2.7 N·m，观察2台电机的实际转速和转矩变化，结果如图5 b）所示。图5 的原图为四通道示波器采样画面截图，四通道共用时间轴（横轴），而各通道的纵轴零点分别为各通道箭头标示位置（画面左侧）。各通道所表示的物理含义及数值均在图中进行了标示。其中，第一、三通道分别为六相电机和三相电机的转速，对应纵轴每格256 r/min；第二、四通道分别为六相电机和三相电机的转矩，对应纵轴每格4 N·m，下同。由图5 a）可以看出：六相电机在转速突增或突减时，三相电机转速和转矩均未受到明显影响；且由于转动摩擦系数的存在，在六相电机转速较高的稳态时，六相电机的输出转矩略高于2.7 N·m。由图5 b）可以看出，六相电机在转矩突增或突减时，三相电机的转速和转矩均未受到明显影响。

图5 六相电机状态突变的试验结果Fig.5 Experimental results of mutation of six-phase motor state

2.2 三相PMSM负载和转矩突变的动态试验

将三相电机转速给定，由200 r/min 突变为300 r/min，待稳定后再突变为200 r/min，观察2 台电机的实际转速和转矩变化，结果如图6 a）所示；将三相电机的负载给定，由2 N·m突变为0 N·m，待稳定后再突变为2 N·m，观察2 台电机的实际转速和转矩变化，结果如图6 b）所示。

图6 三相电机状态突变的试验结果Fig.6 Experimental results of mutation of three-phase motor state

由图6 a）可以看出：三相电机在转速突增或突减时，六相电机转速和转矩均未受影响；且由于转动摩擦系数的存在，在六相电机转速较高的稳态时，六相电机的输出转矩高于2 N·m。由图6 b）可以看出，三相电机在转矩突增或突减时，六相电机的转速和转矩均未受影响。

由串联系统的动态试验可知，当该串联系统中任意一台电机的转速或负载发生突变时，另一台电机的运行状态完全不受影响，本文所提控制策略能够实现2台电机的解耦运行。

3 结论

本文针对单逆变器驱动的凸极式对称六相和三相PMSM 双电机串联系统，研究了基于载波调制PWM 技术的id=0 矢量控制策略，建立了串联系统的数学模型，给出了电压补偿以及电压给定值的叠加方法、电流限制方法、直流母线电压的分配方法和注入零序信号的直流母线电压率的改善策略等。通过2台电机在负载突变和转速突变的动态试验，验证了串联系统在所提控制策略下能够实现2台电机的解耦独立运行。