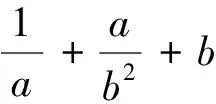对一道二元函数最值问题求解的多视角探究

安徽省合肥市肥东县城关中学 (231600) 王东海

1 考题呈现

(2023届高三武汉市重点高中4月联考第16题) 已知正实数x,y满足xy2(x+y)=9,则2x+y的最小值为.

分析：本题是二元方程约束条件下的二元目标函数最值问题,试题简洁、优美,设有陷阱并有一定的难度,呈现出一定的综合性与选拔性,需要较高的逻辑推理、数学运算、直观想象等核心素养.可以通过均值不等式法,或消参减元法,也可采取数形结合的方法来处理.

2 解法探究

视角1 观察到约束条件为四次式,故考虑对约束条件进行降次,然后用基本不等式法处理.

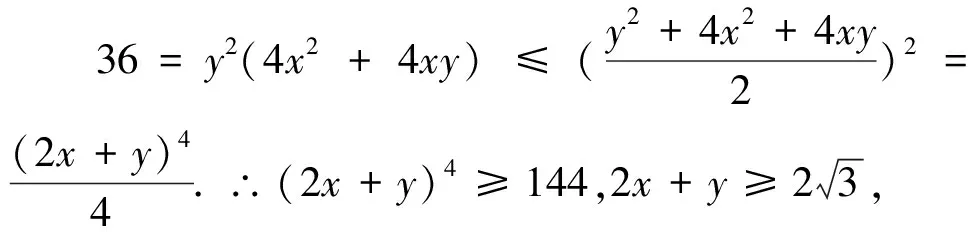
视角2 如果将约束条件换个角度配凑,也能凑成可以使用均值不等式的式子.

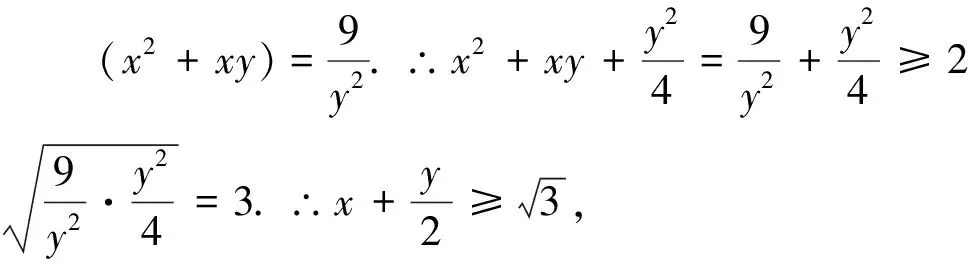
视角3 对于约束条件下的目标函数最值问题,还可设目标函数为k,进而设法去求k的最值.

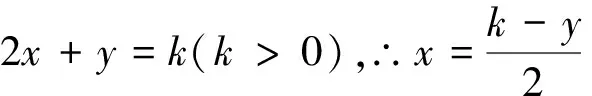
视角4 除了将约束条件降幂思路外,我们也可以对目标函数升幂来处理.

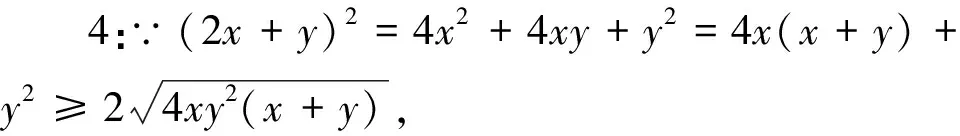
视角5 考虑2x+y=x+(x+y),而约束条件中也有同样的部分,故可以双换元来处理.

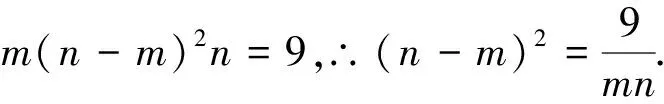
视角6 对于二元约束条件,我们可以用一个变量表示另一个,从而达到消参减元的目的.

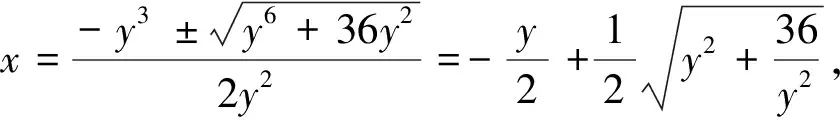
视角7对于解析1、2配凑法往往较难,那么可以考虑用待定系数法可以很快实现配凑.

解析7:∵mx+ny+ny+(x+y)=(m+1)x+(2n+1)y(m,n>0)≥

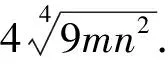
视角8 将2x+y设为S,则可看成一条曲线,而约束条件也看成曲线,故考虑数形结合解决.

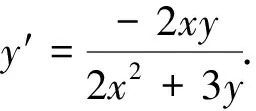
3 命题背景分析

本题命制的背景是拉格朗日乘数法求极值问题.其基本原理是:设给定二元函数z=f(x,y)和附加条件φ(x,y)=0,为寻找z=f(x,y)在附加条件φ(x,y)=0的极值点,我们可以先构造拉格朗日函数L(x,y,λ)=f(x,y)+λφ(x,y),由于φ(x,y)=0,我们可以发现z=f(x,y)的极值即为L(x,y,λ)的极值,且与λ无关.此时分别求L(x,y,λ)对x,y,λ的一阶偏导数,令它们等于零,即

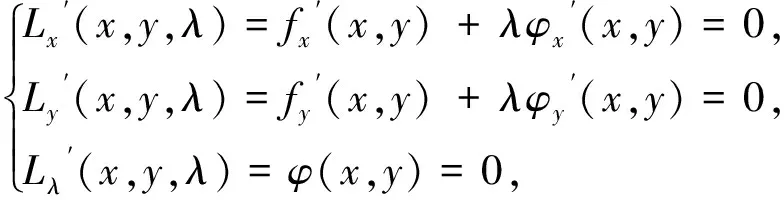
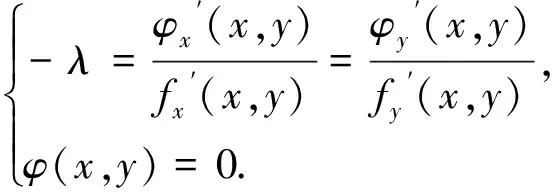
拉格朗日乘数法的优点是:一是把目标函数和等式约束统一到一个拉格朗日函数中;二是将条件最值问题转化为无条件最值问题.

应用拉格朗日乘数法解答考题如下:

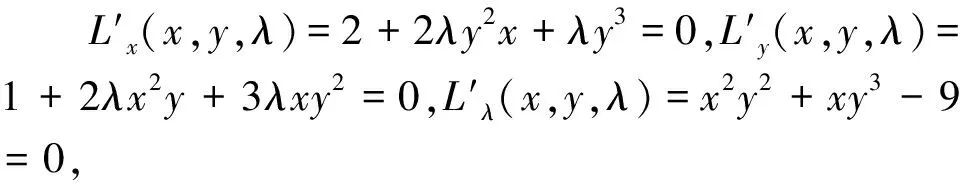
4 高考溯源

题1 (2022年全国Ⅱ卷12题)若实数x,y满足x2+y2-xy=1,则( ).

A.x+y≤1 B.x+y≥-2

C.x2+y2≤2 D.x2+y2≥1

题2 (2020年江苏高考)已知5x2y2+y4=1(x,y∈R),则x2+y2的最小值为.