基于无抽样离散小波变换的复杂纹理织物疵点检测

杨晓波

(浙江树人学院,浙江 杭州 310015)

近年来,小波变换因具有多分辨率特性已被广泛应用于织物纹理检测领域。小波变换可以实现局部增强,由于织物疵点大多分布在局部区域,利用小波变换可以对疵点进行聚焦检测。Sarraf等[1]选用Daubechies D2[2]小波基对织物纹理图像进行滤波,利用分形理论[3]提取织物特征,对包含25种疵点类型的3 600幅织物进行检测,检测精度达到89.5%,但检测速度较低,仅为30.48 cm/min;Han等[4]采用自适应分解尺度小波提取共生矩阵对子图像进行分析,该方法实时检测能力较弱;Yang等[5]通过图像增强突出织物的纹理特性,该方法只对部分种类织物疵点具有较强响应,存在一定的局限性;Jasper等[6]也采用自适应小波基进行织物疵点检测,由于疵点样本较少,且其采用的标准小波变换平移可变,不适合检测细小局部疵点;Yang等[7-8]采用非采样自适应小波提取差异特征进行疵点检测,检测精度达到97.5%,该方法对简单纹理的织物疵点检测精度较高,对于复杂纹理或花色织物的疵点检测精度仍较低。鉴于此,本文采用无抽样离散小波,通过自适应选择小波分解尺度对复杂纹理织物疵点进行检测,增强分解后的图像疵点区域,采用多尺度小波分解的图像融合方法对织物疵点进行实时检测。

1 无抽样离散小波变换原理

由于标准小波平移后会发生能量变化,因而不适用于图像检测和识别领域。无抽样离散小波能够对图像信号进行综合处理,且具有平移不变特性,因而对不同位置图像的检测结果依然保持稳定。

一维无抽样小波的分解计算通过高通和低通滤波器进行卷积操作完成,如式(1)(2)所示:

(1)

(2)

式中:j表示小波分解尺度;n表示分解尺度个数;*表示卷积运算;cj和wj分别表示无抽样小波分解在尺度j上的逼近值和小波系数;cj+1表示在cj基础上的小波分解系数;wj+1表示在不同方向上的小波分解系数;hj和gj分别表示尺度j上的高通与低通滤波器脉冲响应系数。

二维无抽样小波的分解可通过扩展一维无抽样小波分解得到,经过行变换和列变换可以将一维无抽样小波扩展为二维无抽样小波,如式(3)～(6)所示:

(3)

(4)

(5)

(6)

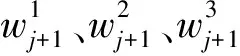
cj+1、wj+1与cj的尺度相同,当疵点分布于织物的不同位置时,二维无抽样小波具有平移不变特性,有利于准确检测织物疵点。

2 小波选择与疵点判定

疵点判别通过分析图像区域的能量变化来实现。由于疵点中的像素比正常纹理像素更亮或更暗,因此图像经过预处理后,疵点区域的能量分布与正常区域存在差异,经过无抽样离散小波处理后,疵点区域的能量增强,与此同时,正常区域的能量减小,从而两类区域的能量差异进一步扩大,有利于判别织物疵点。织物疵点的判别流程如图1所示。

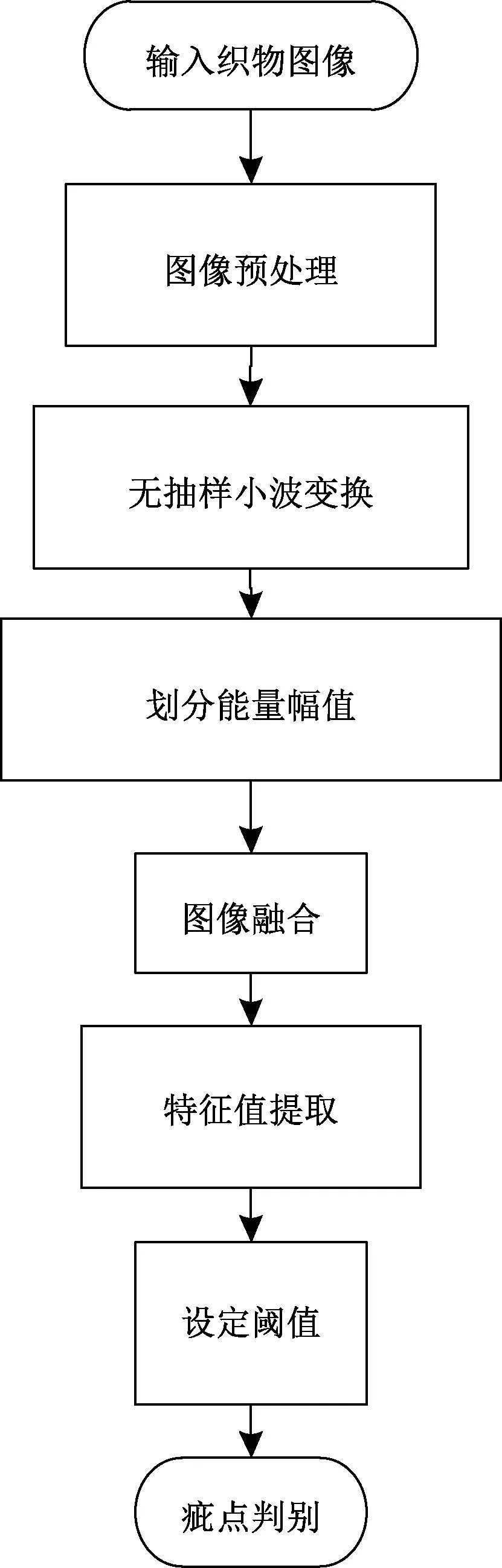
图1 织物疵点判别流程图Fig.1 Flowchart of fabric defects identification

从图1可知,获取织物图像后,首先进行图像预处理,然后利用无抽样小波将像素信息转化为频率域,并划分能量幅值,图像经融合处理后便可提取相应的特征值,最后设定阈值,超过设定阈值时即判定存在疵点。

2.1 小波基和分解尺度选择

利用无抽样离散小波进行疵点判别,关键是要选择合适的小波基和小波分解尺度。小波基的选择主要考虑两大因素,其一是小波基的数学特性,重点考察小波基的正交性、紧支撑和消失矩阵等;其二是所选小波基能够突出图像的局部特征。由于Daubechies D2小波[2]可以实现快速小波转换,同时具有正交性、连续性和紧支撑性,分解过程计算量较小,因而本文选用Daubechies D2小波作为小波基,对织物的各类疵点进行检测。

小波分解尺度的选择需要考虑织物图像的纹理特征,复杂纹理的织物图像包含的信息量较大,选择分解尺度时需突出疵点的能量信息,选择的尺度以适中为宜,因为尺度过大将增加算法的计算量,不利于实时性检测;尺度过小则会遗漏较小的疵点信息,检测效果下降。

由于织物表面纹理具有较强的周期性,正常纹理的能量将向固有频率点集中,疵点区域的能量分布则相对分散。另外,不同织物的纹理周期存在差异,因此纹理的固有频率点也存在不同。

由于疵点区域与正常区域的能量分布在不同区域,因此在选择小波的分解尺度时应满足的条件为:

(7)

式中:FD表示疵点的通带频率;FTi表示正常纹理在i方向上的阻带频率,i=1,2,3分别表示水平、垂直和对角线方向。

通过式(7)可以得到小波分解尺度的最小值,由于不同方向上的织物纹理存在不同的固有频率点,因此在选择小波分解尺度时也应有所不同。

不同类型的织物疵点所需要的小波分解尺度不同,为了保证疵点检测的通用性,从最小的小波分解尺度开始,采用连续的小波分解尺度簇用于检测各种类型的疵点,分解尺度簇经过Daubechies D2小波变换后输出,输出的小波系数为:

(8)

式中:Owc为输出小波系数;h、v和d分别为水平、垂直、对角线3个方向的起始尺度;N为分解尺度的总个数。

2.2 特征提取和疵点判定

织物图像经过无抽样离散小波变换后,可以得到空间能量频谱分布,提取相关的能量特征即可判别纹理图像中是否存在疵点,具体的能量特征值为:

(9)

(10)

(11)

式中:HE、VE、DE分别表示水平、垂直和对角线方向的幅值能量;CPi表示在i方向的小波系数。

特征提取的流程如图2所示。提取织物的图像特征,首先需累积图像区域的幅值,从而获得累积向量,接着计算累积向量的能量,当累积向量的能量大于直接求取的图像能量时,则认为该区域存在疵点,否则认为该区域为正常织物纹理区域。

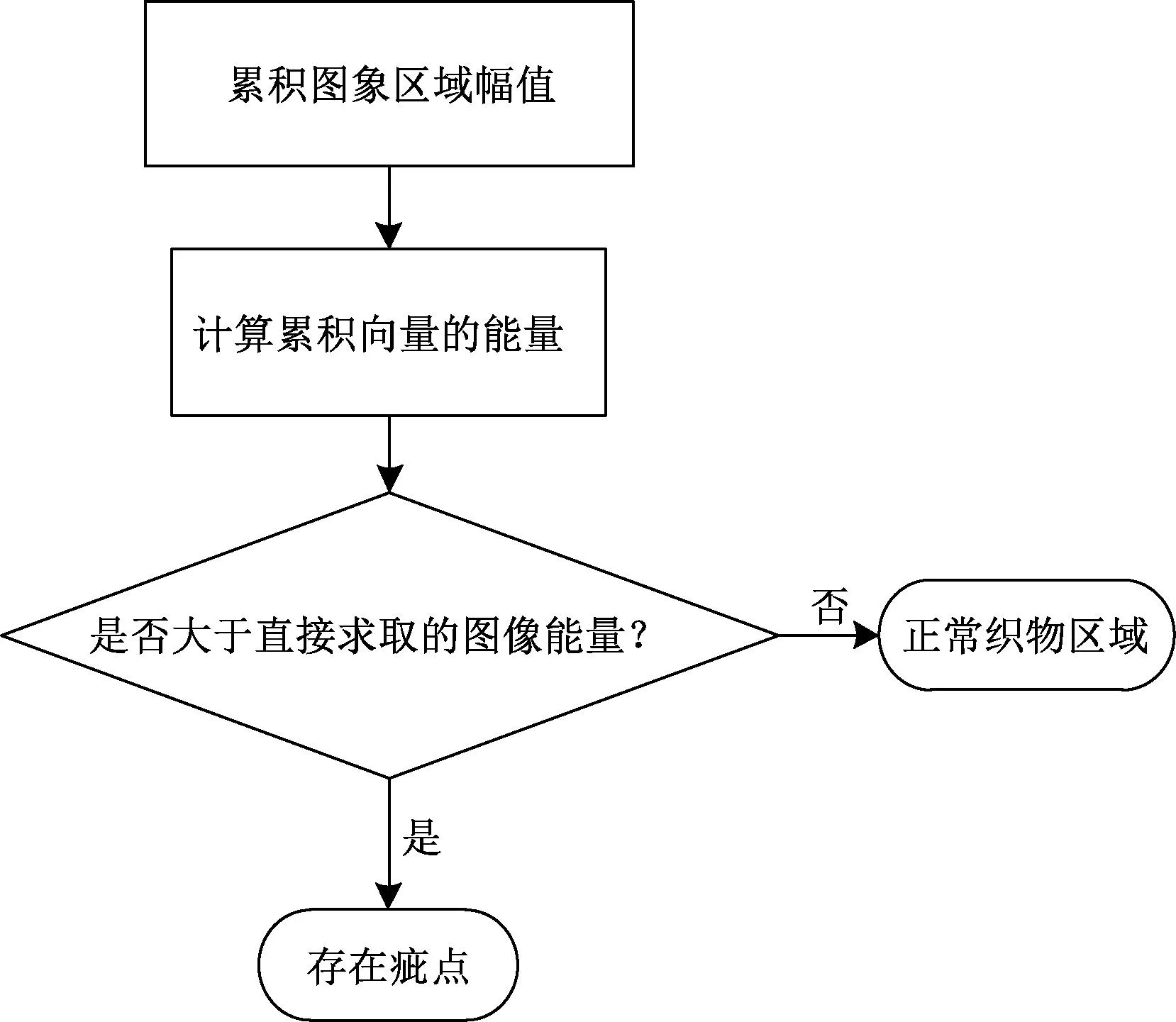
图2 织物图像特征提取流程图Fig.2 Flowchart of feature extraction of fabric image

进行疵点判定时,首先从织物图像区域中提取HE、VE、DE3种能量特征;接着将这3种能量与设定的阈值进行比较,当任何一种幅值能量超出设定阈值,则判定该区域存在疵点,否则可认为该区域为正常纹理。该判定方法不仅能判定疵点的准确位置,而且可以检测出疵点的特征,如该疵点的构成要素是暗像素还是亮像素。

3 对比实验

为了验证无抽样离散小波检测方法的可行性,测试样本选用常见的花色织物疵点类型,采用无抽样离散小波检测方法对不同类型的织物疵点进行检测。实验选用XLP8K6C-H-F4型CCD线阵相机(深圳市度申科技股份有限公司)获取疵点样本,织物表面分辨率设定为0.358 mm/像素,疵点样本图像的大小为512像素×512像素,每个检测图像的子区域设定为64像素×64像素。

本文实验累计采集图片总数54 006张,其中合格样本图像 30 242张,疵点样本图像23 764张,采用本文算法对检测样本进行测试,通过分析检测正确率和误判率,评定最终的检测结果。选用的常见花色织物疵点种类如图3所示。

图3 8种常见花色织物疵点Fig.3 8 types common fabric defects in different patterns and colors.(a)Broken picks; (b) Missing end; (c) Hole; (d) Nep(e) Oil contamination; (f) Square eye;(g) Drop stitch; (h) Coarse knot

当织物出现疵点时,正常织物的纹理模式将会发生变化,疵点区域的内部像素变化有别于正常纹理区域。检测过程中,选取断纬、缺经和油污为有代表性的花色织物疵点,采用的无抽样小波分解尺度个数为2,对图像进行分解,所得结果如图4所示。

图4 3种花色织物疵点的无抽样离散小波检测结果Fig.4 Non-sampling discrete wavelet detection results of three color fabric defects.(a) Broken weft; (b) Horizontal energy diagram; (c) Testing result;(d) Lack of warp; (e) Vertical energy diagram; (f) Testing result; (g) Oil contamination; (h) Horizontal energy diagram; (i) Testing result

选用常见花色织物的漏针、破洞和棉结类型疵点进行检测,对应的无抽样小波分解尺度个数分别为2、1和3,所得结果如图5所示。

图5 另外3种花色织物疵点的无抽样离散小波检测结果Fig.5 Non-sampling discrete wavelet detection results of another three color fabric defects.(a) Drop stitch; (b) Horizontal energy diagram; (c) Testing result;(d) Hole; (e) Vertical energy diagram; (f) Testing result;(g) Nep; (h) Horizontal energy diagram; (i) Testing result

从图4和图5可知,当疵点类型不同时所采取的小波分解尺度数也要相应改变,这样才能得到较好的检测结果。为了客观分析小波分解尺度个数与各类疵点检测能力之间的关系,可以通过计算疵点区域特征平均值与正常区域特征平均值的比值(见式(12))对其进行判定。

(12)

式中:Ui代表某种疵点在疵点区域中的特征值;Uj表示在正常纹理区域所获得的特征值;p为疵点判别指数。

当计算所得p值较大时,则说明疵点区域与正常区域差异明显,可以设定正常区域对应的p值为阈值,超过设定阈值即可判定存在疵点。

利用不同小波分解尺度对各类织物疵点进行检测,检测结果如图6所示。随着小波分解尺度个数的增加,6种类型疵点的判别指数也随之增加,表明当小波分解尺度个数增加时,计算量会随之加大,检测精度也会相应增加。缺经疵点频率响应主能量区与正常纹理的频率点较为接近,因此只需1个分解尺度就能判别织物的疵点区域。其他类型的疵点频率响应主能量区与正常纹理的频率点相差较远,因而需要较高的分解尺度提取特征值,如脏纬、松经、断纬和棉结疵点都需要2个及以上分解尺度才能获得较好的检测效果;当小波分解尺度个数为3时,疵点判别指数较大。

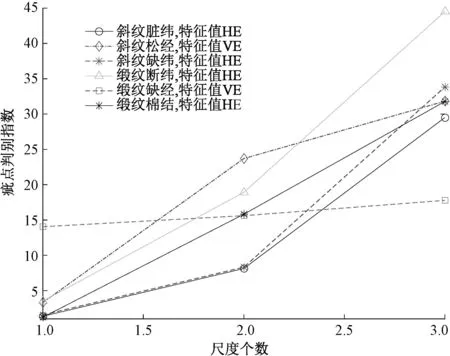
图6 不同小波分解尺度对各类织物疵点的检测结果Fig.6 Detection results of fabric defects with different wavelet decomposition scales

小波分解尺度的自适应选择取决于待测织物的纹理和疵点频率特性,纹理不同则对应的小波分解尺度不同,同时不同的频率反映不同的图像信息,因此在选择小波分解尺度时,尽可能选择能够使疵点频率增强的尺度。

为了表明无抽样离散小波适合于织物疵点检测,分别选用常见的主流算法[9-11]与本文无抽样离散小波检测算法进行实验,并对结果进行对比分析。实验采用100幅大小为512像素×512像素的疵点图像样本和150幅大小为512像素×512像素的正常纹理疵点图像样本进行检测,疵点类型分别选取断纬、缺经、油污、漏针、破洞和棉结,检测结果与织物疵点国家样照进行比对,与国家样照一致定为正确,反之则为不正确,对比结果见图7。

图7 对比实验结果Fig.7 Comparative experimental results

从图7可知,无抽样离散小波算法的平均正确率达到97%,高于其他主流检测方法,说明无抽样离散小波算法比较适合于检测复杂纹理织物疵点。

另外,为了检验疵点识别算法的实时特性,本文采用4种不同的疵点检测算法对织物疵点进行实时检测,检测结果见表1。

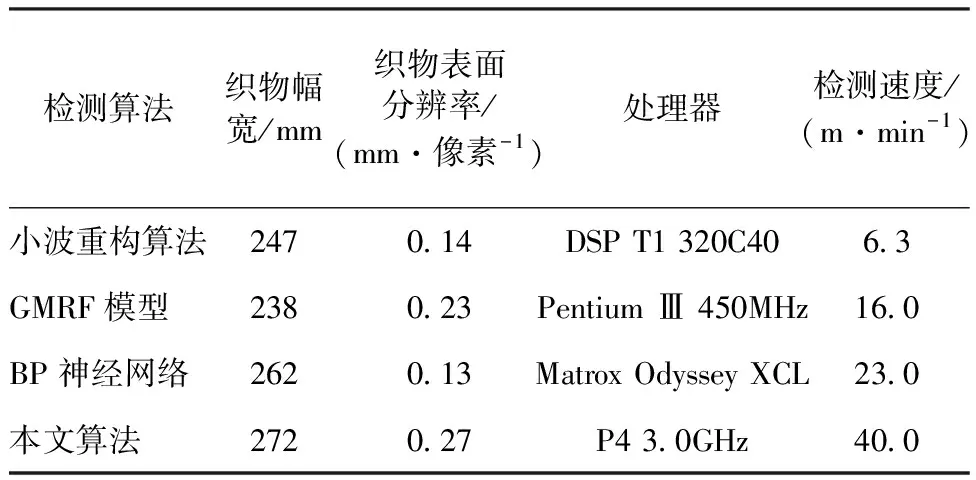
表1 不同处理器的疵点检测结果Tab.1 Defect detection results for different processors

从检测结果来看,织物幅宽较为接近,不同处理器结合不同检测算法,检测速度存在较大差异,无抽样离散小波检测法的检测速度高于其他3种检测算法,表明无抽样离散小波检测法的实时检测性能较优。

4 结 论

为了提高织物疵点的检测精度,本文提出一种基于无抽样离散小波变换算法,通过算法分析和对比性实验得出以下结论:

①无抽样离散小波平移不变特性有利于准确检测分布于织物的不同位置疵点。经过无抽样离散小波处理后,疵点区域的能量增强,正常区域的能量减小,区域的能量差异变大有利于判别织物疵点。

②选用Daubechies D2小波作为小波基对织物的各类疵点进行检测。小波分解尺度的选择需要考虑织物图像的纹理特征,选择的尺度以适中为宜。

③从织物图像区域中提取水平、垂直和对角线方向能量作为特征值,与设定的阈值进行比较,判定该区域是否存在疵点,该判定方法不仅能判定疵点的准确位置,而且可以检测出疵点的特征。

④分别选取6种类型的织物疵点进行对比实验,无抽样离散小波算法的平均正确率达到97%,高于其他3种主流检测方法,说明无抽样离散小波算法比较适合于检测复杂纹理织物疵点;无抽样离散小波检测法的实时检测性能优于其他3种主流检测算法。