基于T-S模糊神经网络的光伏发电机组自动控制
2024-03-08杨振睿沈主浮
杨振睿,沈主浮,孙 辰,蔡 斌,姜 宽
(1.国网上海市电力公司市区供电公司调度控制中心,上海 200080;2.国网上海市电力公司市区供电公司总师室,上海 200080)
0 引言
太阳能作为一种应用较为普遍的可再生能源,环保效果显著,因此其广泛应用在电力系统中[1]。光伏发电主要由光伏发电机组完成,该机组由多个部分设备组成,包含光伏阵列、蓄电池组等。光伏发电机组在运行过程中,具有出力随机波动[2]、转动惯量变化显著等特性,导致直流近区电网较为薄弱,对电网的暂态稳定造成了不利影响[3]。在光伏接入量较大时,转动惯量会大幅度降低,直接影响整个电网的安全稳定运行。因此,进行光伏发电机组的自动控制可保证电网稳定运行。
为实现光伏发电机组的自动控制,汤茂东等[4]和樊国东等[5]分别基于离散一致性算法和基于负荷频率协调优化实现光伏机组的自动控制。上述方法均具有一定的控制效果,但是在控制过程中,对于最大功率点跟踪效果不高,导致控制质量大幅度下降。因此,为了提升光伏机组自动控制能力,本文对光伏机组进行详细研究和分析后,依据光伏机组的结构和运行特点,提出基于T-S模糊神经网络[6]的光伏发电机组自动控制方法。
1 光伏发电机组自动控制方法设计
1.1 光伏发电机组系统
1.1.1 光伏阵列数学模型
由于电网中大量接入光伏发电机组后,其与直流近区电网之间的连接导致直流近区电网薄弱[7],因此,为保证光伏发电机组自动控制效果,需通过建立光伏发电系统模型,分析光伏机组特性。光伏发电机组和直流输电系统是光伏发电机组重要组成部分,光伏阵列和母线之间的接入通过逆变器完成,功率输出则经由直流输电系统完成。
光伏阵列是光伏发电机组中的重要发电设备之一,在实际应用中,为分析其伏安特性需构建数学模型,该模型构建时需参考光伏阵列厂家提供的组件参数[8]。假设光照强度和电池板温度分别为S和T,则此时光伏阵列的数学模型公式为
(1)
式中:i1为输出电流;u1、usc为不同端口电压;uoc为开路电压;isc为光伏发电组件中,光子激发产生的电流;um为最大输出大功率点m处的电压;im为m点的电流;C1、C2为不同的调节系数。
由于光伏阵列的实际和参考2个工作条件之间存在差异,则在实际情况下的uoc、isc、um、im的计算公式为
(2)
式中:a、b、c为常数;Sref和Tref分别为对应光照强度、光伏电池板温度参考值;uocref和iscref分别为开路与短路情况下的电压和电流;umref和imref分别为最大功率点的电压和电流。
光伏阵列最为普遍的是集中式结构,该结构由多个光伏组件组成[9],且组成方式为并联和串联。在不考虑接线损耗和组件差异的情况下[10],光伏阵列端口处的电压和电流计算公式为
(3)
式中:udc和iPV分别为光伏阵列端口处电压和电流;Ns和Np分别为串联组件、并联组件数量。
依据式(3)即可对单个光伏组件的电压和电流进行求解;获取集中式光伏阵列的数学模型,将求解结果代入式(1)中得出,其计算公式为
(4)
1.1.2 光伏阵列特性
依据1.1.1小节的分析可知,S会对光伏阵列产生直接影响,而温度直接随着光照强度的增强而增加,光照强度越高,光伏输出功率也越高[11]。因此,正常情况下,存在2种光照情况,第1种为均匀光照、第2种为不均匀光照。在第1种情况下光伏阵列的P-V曲线中的极值点只有1个,点即为MPP;在第2种情况下光伏阵列P-V曲线中的极值点存在局部和全局2种,则存在多个MPP。2种光照情况下的光伏阵列特性曲线结果如图1所示。
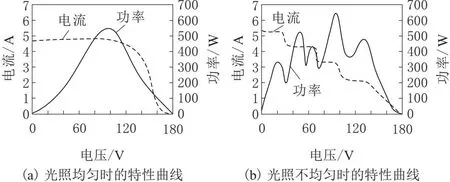
图1 光伏阵列特性曲线
1.2 光伏发电机组自动控制
1.2.1 自动控制方案制定
根据上述分析得出,光伏发电机组在发电过程中,S是影响光伏发电机组运行状况的主要因素,同时,在实际环境中,S的变化存在随机性和实时性,因此也导致存在随机性和实时性的变化特性。而对光照和温度的实时跟踪[12],是实现光伏发电机组自动控制的基础,因此需要迅速跟踪最大功率点(MPPT)。文中采用基于T-S模糊神经网络对MPPT实行控制,制定控制MPPT的控制方案,其结构如图2所示。
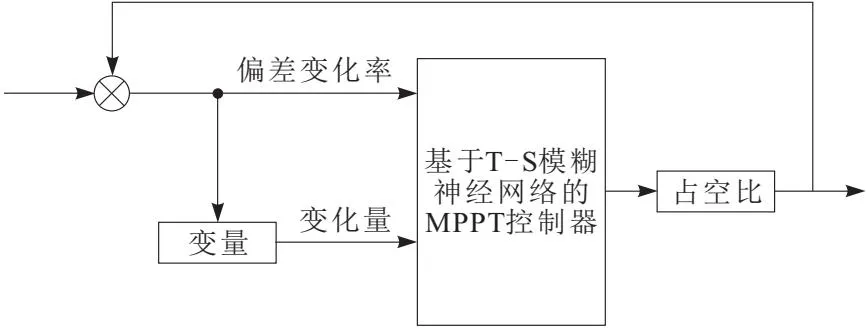
图2 光伏发电机组自动控制方案结构
该控制方案在对MPPT实行控制时,可对升压电路的绝缘栅双极型功率管的占空比进行调整,保证光伏阵列的运行一直处于最大功率点的位置[13]。当偏差变化率e(k)等于0时,光伏阵列则一直处于最大功率点位置,因此,为获取该时刻的输出功率P(K),需获取光伏阵列在各时刻输出的电压U(K)和电流I(K)的测量结果。Δe(K)表示e(K)的变化量,最大功率点控制器的输入即为Δe(K)和e(K),并且对其在k和k-1此2个时刻下的状态实行对比和判断,以此调整占空比的大小。
1.2.2 光伏发电机组自动控制模型
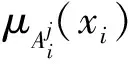
a.模型前件网络,该网络部分包含4个层:
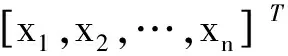
第3层为规则层:为获取所有模糊规则的适应度结果,需对全部的模糊规则前件实行匹配,完成匹配后计算权值ωj结果,该计算采用乘积法完成。
第4层为归一化层:采用归一化的方式完成ωj的处理,并将处理结果作为模型后件网络部分中第3层的连接权值,则归一化的处理公式为
(5)
b.模型的后件网络部分:该网络部分共由3层组成,第1层与前件部分相同;第2层则对所有的模糊规则输出量实行计算,如果输入的变量用xi表示,则第j层的输出量ulj的计算公式为
(6)


当控制规则相同时,如果后件网络参数较多,则会增加上述参数调整的难度,对模型实行简化处理,以此减少后件网络部分中的参数,则权值学习过程中,误差代价函数E的计算公式为
(7)
式中:yr、yt分别为期望和实际2种输出值。

(8)
式中:β为学习速率。
结合最佳跟踪结果和自动控制模型实现光伏发电机组自动控制。
2 测试分析
为测试本文方法对于光伏发电机组的控制效果,将本文方法用于某电力企业的直流近区光伏发电系统中,测试本文方法的应用效果,该系统结构如图3所示。
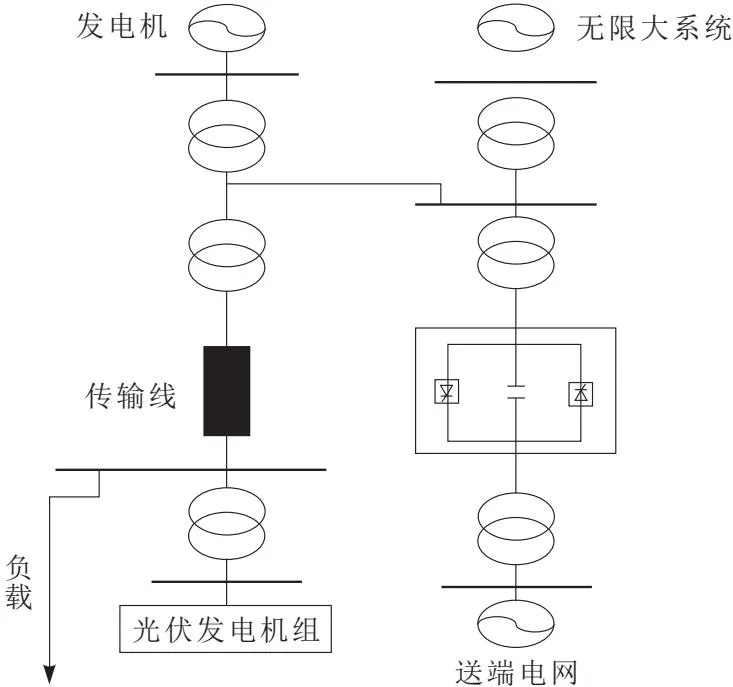
图3 直流近区光伏发电系统
该系统中的直流输电电压为850 kV,光伏电站的相关参数详情如表1所示。
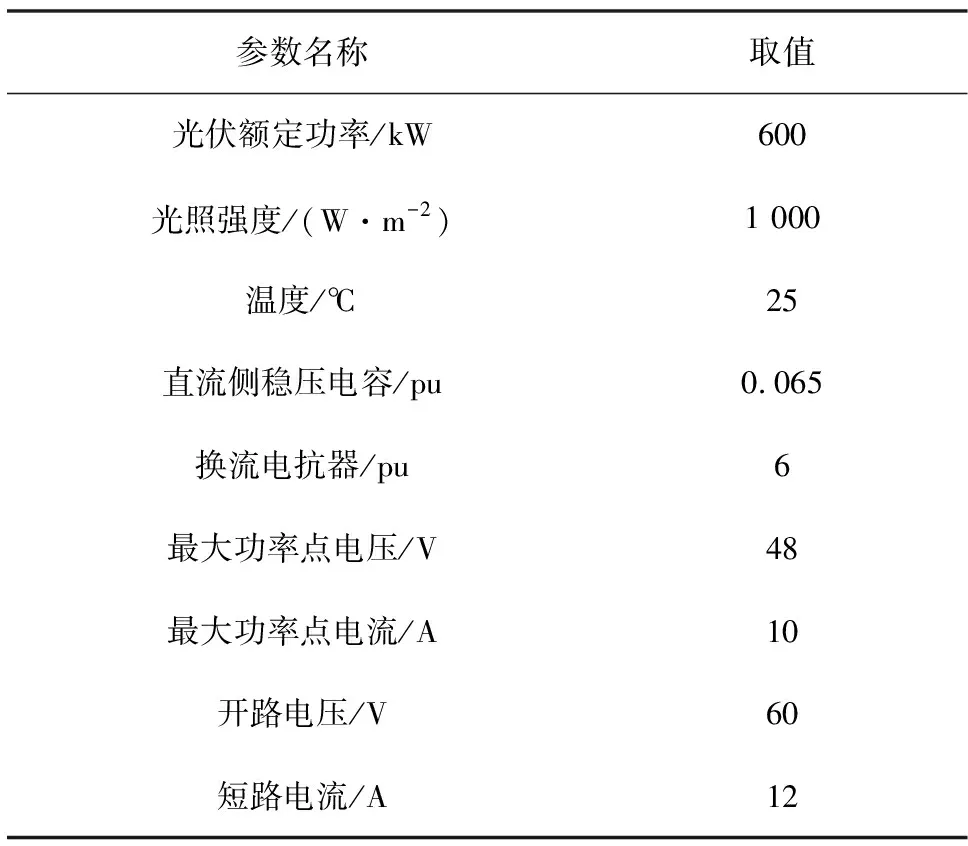
表1 光伏电站的相关参数
为衡量本文方法对于光伏发电机组特性的分析可靠性,获取光照强度变化情况下,光伏阵列功率和电压输出结果,如图4所示。前40 s光照强度为1 000 W/m2,40~120 s光照强度为550 W/m2,120~180 s光照强度为800 W/m2。
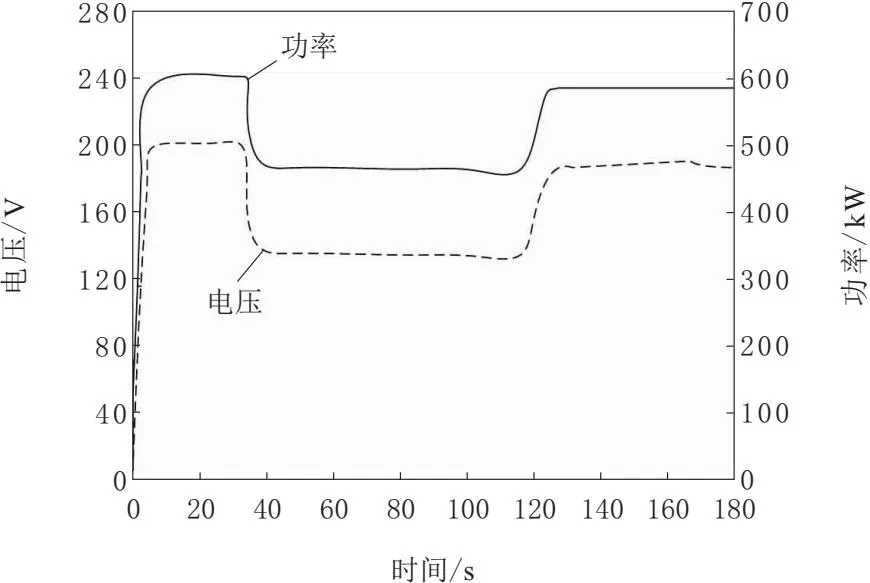
图4 光伏阵列功率和电压输出结果
由图4可知,光伏阵列的输出功率和电压在光照强度发生变化后,也随之发生变化,表明光伏阵列输出功率和电压会受到光照强度的直接影响,与实际情况吻合。
为衡量本文方法的应用效果,以光伏阵列MPPT的跟踪作为衡量标准,获取本文放在不同光照情况下,对于光伏阵列MPPT的跟踪结果,如图5所示。
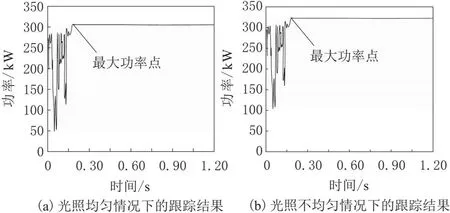
图5 光伏阵列MPPT的跟踪结果
由图5可知,在2种光照情况下,本文方法均可完成光伏阵列MPPT的跟踪,且跟踪所需时间均在0.3 s以内,能够有效跟踪MPPT。即使光照不均匀,导致MPPT的变化发生显著波动情况下,本文方法依旧能够快速完成MPPT跟踪。
为进一步衡量本文方法的应用效果,获取本文方法对光伏发电机组实行自动控制后,不同时刻功率的波动结果,并将该结果与控制前的功率波动结果实行对比,判断本文方法对功率波动的控制效果,结果如图6所示。

图6 功率波动控制效果
由图6可知,经过本文方法控制后,功率的波动变化值被平稳控制在260 kW以内。表明本文方法的自动控制效果良好,能够针对光伏发电输出异常情况实行有效控制,保证光伏发电机组的输出稳定性。
为衡量本文方法的应用效果,采用本文方法获得在2种光照情况下直流近区光伏发电系统在不同时刻内产生的弃光量,期望标准为30%以下,结果如图7所示。
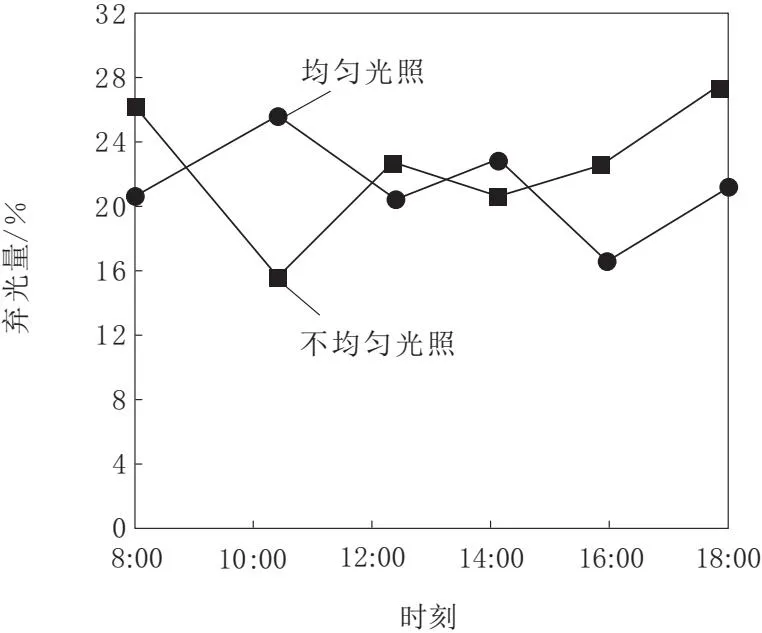
图7 弃光量测试结果
由图7可知,本文方法应用后,在2种光照情况下光伏发电机组的弃光量均在30%以下,满足控制需求。因此,本文方法具有良好的自动控制效果,能够最大程度降低机组弃光量,应用效果良好。
为进一步衡量本文方法的应用,采用本文方法在2种光照情况下,对光伏发电机组实行控制,获取光伏发电机组在不均匀光照下,发生负载突变情况下输出的频率结果,如图8所示。本文的期望频率控制偏差标准低于0.3 Hz。
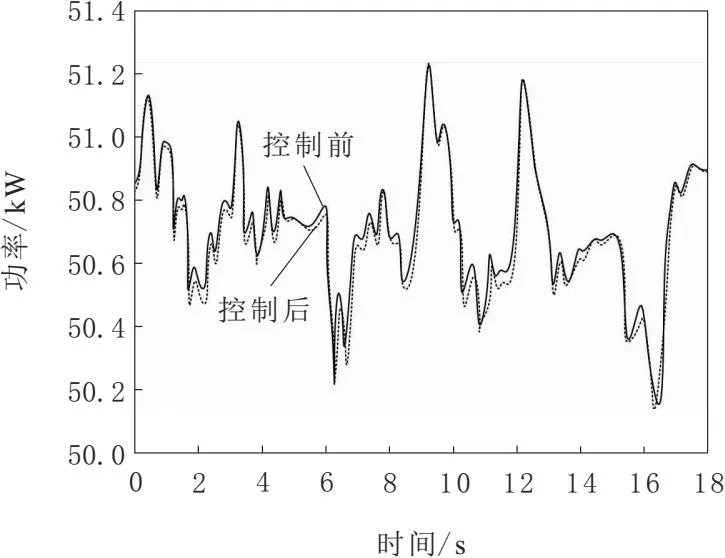
图8 光伏发电机组输出频率控制结果
由图8可知,本文方法控制后,光伏发电机组输出频率结果的最大值和最小值分别为52.2 Hz和48.6 Hz,该结果和理想控制结果之间的偏差值均低于0.3 Hz,因此,本文方法的应用性较好,能够满足控制需求。
3 结束语
光伏发电机组的大量并网,对于电网的稳定存在一定的不利影响,因此,需实现光伏发电机组的自动控制,保证机组的运行状态。本文提出基于T-S模糊神经网络的光伏发电机组自动控制方法。经过相关测试后可知,本文所提方法能够有效分析出光伏发电机组在不同光照情况下的输出特性,并可快速、精准实现最大功率点的跟踪,控制效果良好,控制后光伏发电机组的输出功率和频率均满足控制需求,以此可保证电网的稳定运行。
