结构参数对不锈钢织物透光与电磁屏蔽的影响

池烨馨, 俞科静, 徐 阳

(江南大学 纺织科学与工程学院,江苏 无锡 214122)

从雷达探测、电子侦察、卫星通信到手机通讯、电磁探伤、医疗诊断领域,电磁波技术覆盖在从军事国防到人们日常生产生活的各个领域中。然而,随着各类电子设备及精密仪器电磁兼容要求的日益提升,以及军事、航空航天等领域光电探测、人机交互等系统对电磁防护的需求日益迫切,对电磁屏蔽材料提出了更高的性能要求。因此,高性能电磁屏蔽材料的研究显得十分重要。它不仅有利于解决电磁波引起的电磁干扰问题,而且对提升通讯网络、信息传输、武器装备等安全性、国家安全、社会生活及经济发展具有重大意义[1]。随着现代电子学向柔性和可集成性方向发展,在一些特殊领域如航空视窗、平面显示屏、精密电子器件、军事等都对电磁屏蔽材料的透光性提出了更高的要求[2-3]。因此,设计研发兼具高透光性能和电磁屏蔽性能的材料至关重要。

电磁屏蔽是电磁波在屏蔽体表面的反射和在屏蔽体内的吸收及在屏蔽体内部的多次反射损耗造成的电磁能衰减[4]。电磁屏蔽性能取决于许多因素,如电导率、磁导率和结构,这主要归因于吸收、反射和透射的电磁屏蔽[5]。其中,电磁波的反射和吸收是电磁干扰屏蔽效应的主要电磁衰减机制。材料的电导率越高,与自由空间的阻抗不匹配程度越高,反射损耗越大;吸收损耗则通过将电磁波在材料体内转为热能而耗散衰减[6]。目前以单一材料制备的透明电磁屏蔽织物主要有透明导电氧化物系材料[7]、碳系材料[8-9]、导电高分子聚合物材料[10]及金属系材料[11-12]。金属系材料中,金属纤维或金属化纤维不但具有金属材料固有的优点,还能在一定程度上拥有天然纤维和合成纤维所具有的柔软性[13-15]。其中最具代表性的不锈钢织物,具有高导电、高导磁、屏蔽效能持久、耐洗涤耐腐蚀的特点,在电磁屏蔽领域应用广泛[16]。不锈钢织物的透光性能和电磁屏蔽性能与其结构参数(线径与线距)有关,如图1所示。图1中,p代表线距,mm;d代表线径,mm。线距越小,线径越大,则屏蔽效能越好,但透光性能会降低。因此,如何实现不锈钢织物的高透光率与强电磁屏蔽效率是一个巨大的挑战。

图1 不锈钢织物Fig.1 A stainless steel mesh

本文在分析不锈钢织物主要结构参数对其透光性能及屏蔽效能影响的基础上,基于织物覆盖系数理论与麦克斯韦光的电磁学说,以SUS316不锈钢为例,研究并分析了不锈钢织物的线径与线距对其透光、电磁屏蔽性能及综合性能的影响规律,以期为高透光电磁屏蔽材料的结构设计提供一定的理论支持。

1 结构参数对透光与电磁屏蔽效能的影响

1.1 仪器与设备

Lambda 950 UV-Vis-NIR 分光光度计(铂金埃尔默企业管理(上海)有限公司),Keysight E5063A矢量网络分析仪(深圳市美佳特科技有限公司)。

1.2 结构参数与不锈钢织物透光性能的关系

由于实际生产限制,目前商用SUS316不锈钢单丝直径最小在20 μm左右。根据相关研究,当金属网的线宽远远大于可见光的波长时,可以认为金属引起全反射,金属网的其余部分可以在正常入射下作为总透射[17]。故可见光透光率可用未被遮盖面积占总面积的比例表示[18],如下式所示。

T/%=(1-d/p)2×100

(1)

式中:p代表线距,mm;d代表线径,mm。

根据式(1)通过数值计算方法分析不同线径与线距对不锈钢织物透光性能的影响。由于不锈钢织物最细直径为 20 μm,而不锈钢丝过粗会影响不锈钢织物的柔性,同时为了保证不锈钢织物具有一定的透光率,不锈钢织物的线距设置为0.2、0.4、0.6、0.8 、1.0、1.2 mm。在定线距条件下,讨论不同线径对不锈钢织物透光率的影响,线径-透光率曲线如图2(a)中a1～a6所示;设置不锈钢纤维的线径为0.02、0.05、0.08、0.10、0.12、0.15 mm,在定线径条件下,讨论不同线距对不锈钢织物透光率的影响,线距-透光率曲线如图2(b)中b1～b6所示。

由图2(a)中曲线a6可以看出,在线距为1.2 mm时,随着线径的增大,透光率逐渐降低,且随着线径的增大,曲线a6的斜率逐渐变化,曲线呈现由陡峭到平缓的趋势。a1～a6曲线呈现相同的规律,且六条曲线斜率变化较大的区间都在透光率0～20%内。这说明在线径较大的时候,线径的改变对透光率影响比较微弱,而当线径偏小时,线径的细小变化也会引起透光率的大幅波动。随着a1～a6曲线的线距从0.2 mm增大到1.2 mm,曲线逐渐变得平缓。

图2(b)中曲线b1～b6呈现了与曲线a1～a6相反的变化趋势,在固定线径的前提下,线距越大,透光率越大,且曲线变化从剧烈逐渐变为平缓。其中,曲线b1～b6均表现出相同的变化趋势,且在透光率80%～100%内,曲线斜率变化程度极大。这说明在透光率小于80%时,线距的微小变化就会引起透光率的大幅波动,而当透光率大于80%后,透光率对线距变化的敏感程度降低。

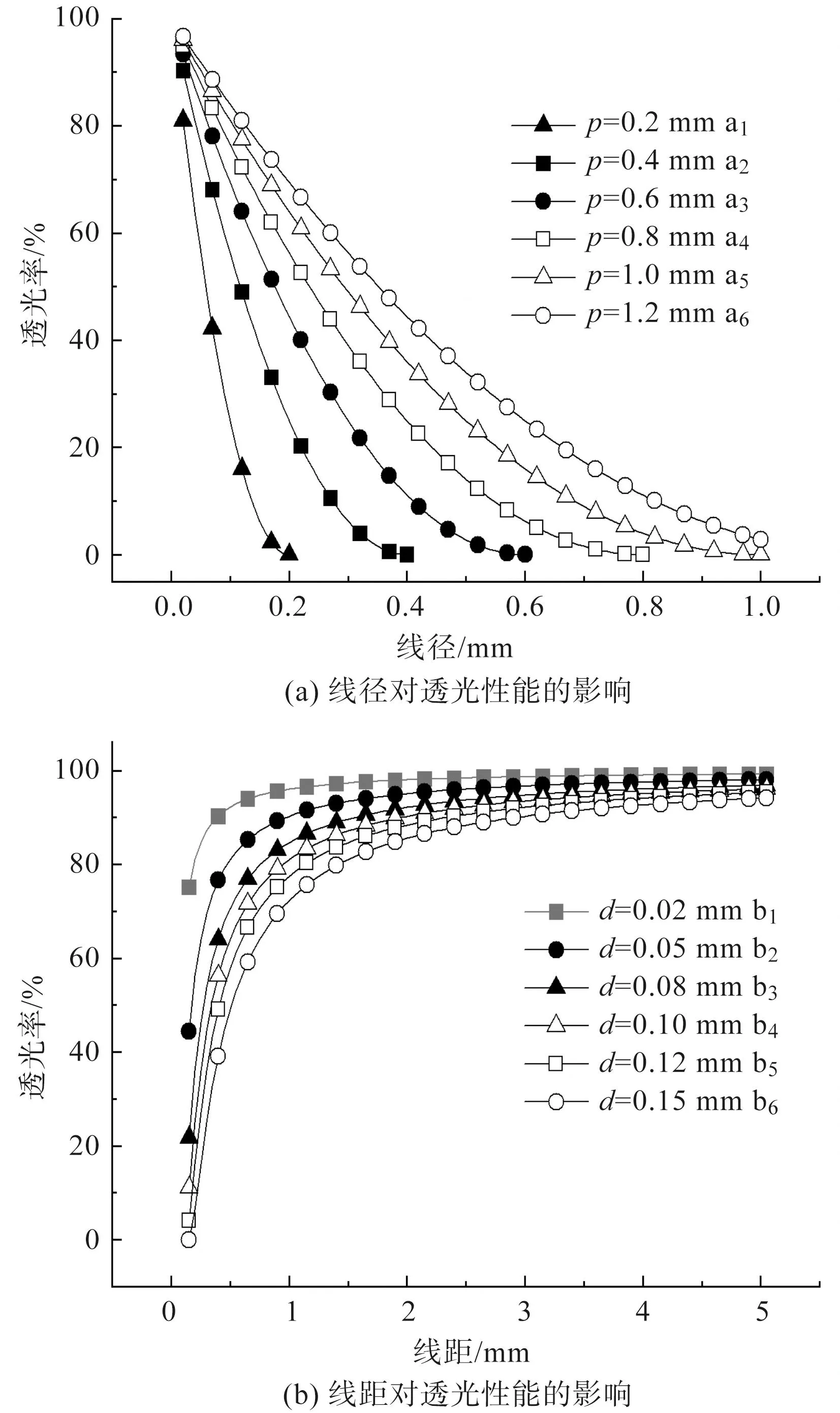
图2 结构参数变化对透光性能的影响Fig.2 Effect of variation of structural parameters on light transmission properties

1.3 结构参数与不锈钢织物屏蔽性能的关系

对于不锈钢织物而言,对电磁波的反射损耗是其实现电磁干扰屏蔽的主要机理。目前对电磁屏蔽性能的测试方法主要有三种,其中法兰同轴测试法设备成台性好,操作简单,频率范围较广包括高低频段,为30～1 500 MHz,测试结果稳定性较好。对于各向同性电磁屏蔽织物的性能测试,基本选用法兰同轴法[19]。

金属丝网屏蔽效能计算模型如下式所示,其在30～1 500 MHz内的计算结果如图3所示。

式中:SE为电磁屏蔽值,dB;p为金属丝交织间距(中心距),m;d为金属丝直径,m;Rf为金属丝单位长度的交流电阻,Ω/m;Xf为金属丝单位长度的电抗,Ω/m;f为频率,Hz。

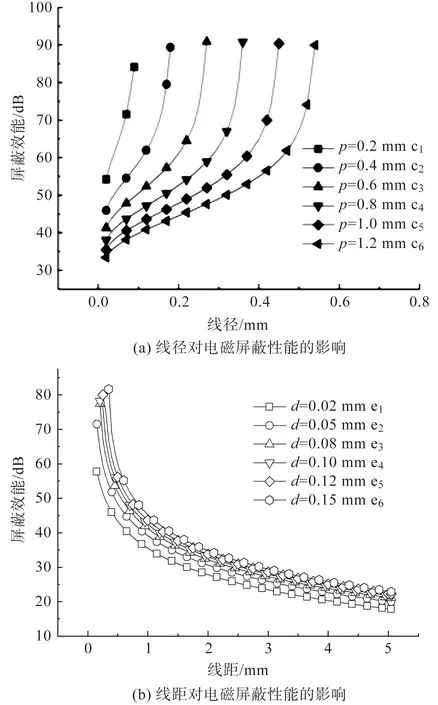
图3 结构参数变化对电磁屏蔽性能的影响Fig.3 Influence of structural parameter variations on electromagnetic shielding performance

由图3(a)中曲线c1～c6可以看出,在固定线距的前提下,随着线径的增加,屏蔽效能呈现由缓转急的变化趋势。当屏蔽效能在55～65 dB时,曲线的斜率变化最剧烈。同时,随着c1～c6曲线线距的增大,曲线呈现整体下移的趋势。这说明线距增大时,线径对屏蔽性能的影响越剧烈,而线距较大时,屏蔽效能的上限趋于接近,下限会逐渐降低。

由图3(b)中曲线e1～e6可看出,在固定线径后,随着线距的增加,屏蔽效能先急速减小后变化缓慢。当屏蔽效能偏低时,线距的变化对其影响变得微弱,当屏蔽效能在40～60 dB时,线距的微小变化也会导致屏蔽效能效率的数量级改变。随着线径的缩小,整体的屏蔽效能会降低,且线径越小,降低幅度越明显,线径较大时,线距-屏蔽曲线更趋于接近。

1.4 结构参数变化对透光与电磁屏蔽性能影响分析

上述结果表明,电磁屏蔽性能随着相同含量导电栅格单元面积的减小而增大,这一方面可能是因为较小的导电光栅面积和导电网格单元的均匀分布增强了电磁波上的阻抗失配和相互作用,从而使更多的电磁波通过反射和吸收而衰减[20]。另一方面,在图2与图3中的多条曲线呈现的非线性规律也可能是由于电磁波在通过不锈钢织物时出现的衍射现象。

利用标量衍射理论对不锈钢织物的夫琅禾费衍射特性分析,可发现其衍射图样中的衍射能量分布呈现十字交叉形,能量大部分聚集在中心次级,沿坐标轴分布着一些强度较弱的点[21]。即衍射到中心阶的能量为最大化,其余的传输能量被衍射到高阶。且根据Ulrich的等效电路模型与传输线理论分析,不锈钢织物的屏蔽效能与其总电磁波透射有关,总电磁波透射较小时,屏蔽效能变化明显,而总电磁波透射较大时,变化减缓[22]。

电磁波入射会发生电磁衍射现象,而这些高阶衍射能量主要影响了成像质量中的杂散光水平,能量越低,杂散光均匀化程度越好。根据惠更斯-菲涅耳衍射理论,一个更大的狭缝(其d减小,p保持不变)会导致更强的光集中。此外,较小的线径有利于抑制杂散光,这一理论验证了图中曲线的趋势[23]。在夫琅禾费平面光栅衍射实验理论的指导下可进行Matlab仿真。通过程序设计,得到衍射光强分布图和条纹分布图,并可从缝宽参数的调整,根据其衍射光强的分布变化,探究其在550 nm可见光入射情况下,结构参数变化对衍射效应的影响[24]。通过Matlab对不同尺寸网格衍射能量分布计算,其结果如图4所示。

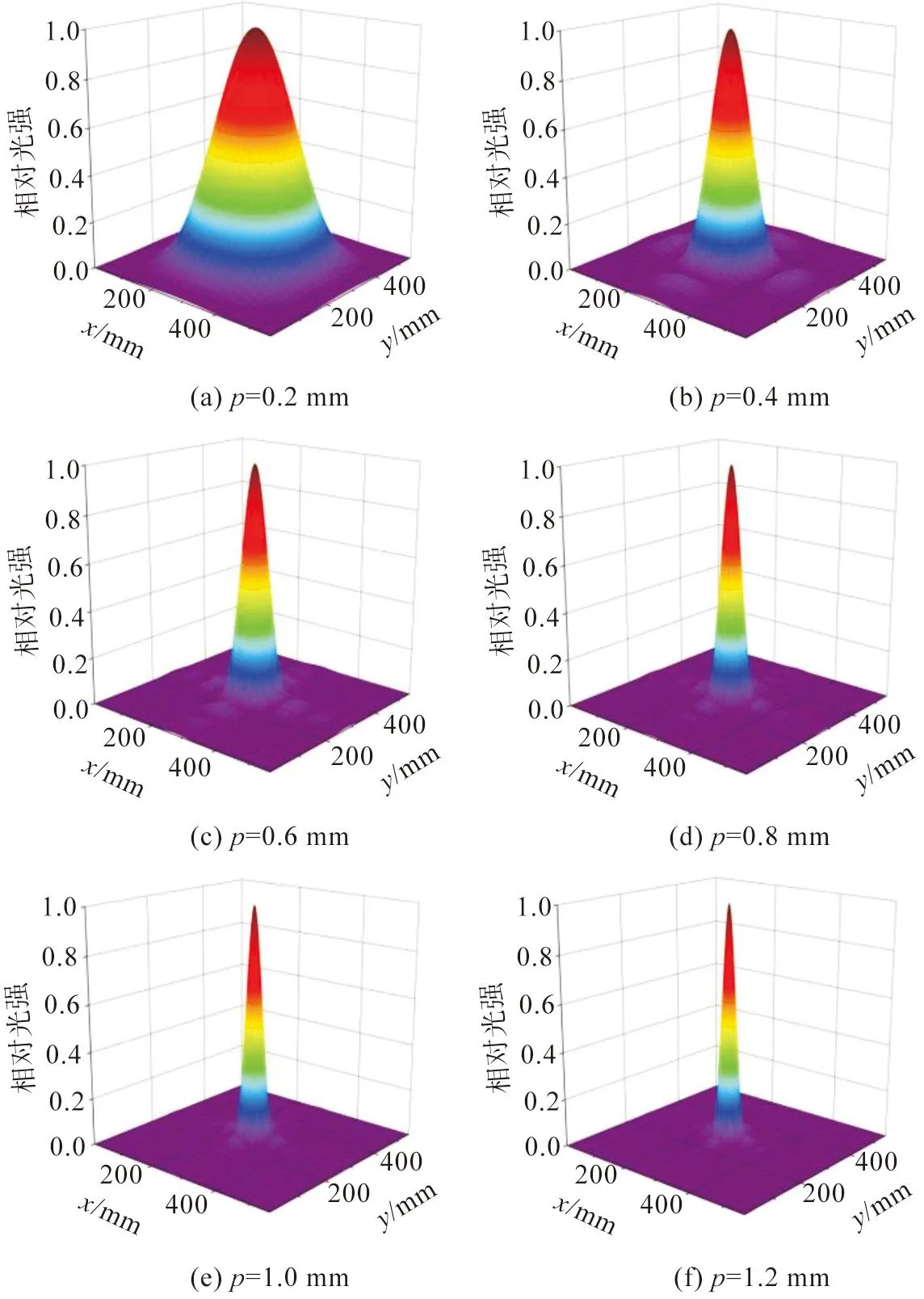
图4 不同尺寸网格衍射能量分布Fig.4 Diffraction energy distribution of different sizes

从图4中(f)到(a),随着线距的缩小,其中心级能量不断增加,高阶衍射能量在(d)到(f)中较为明显,可看出随着尺寸变化高阶衍射能量变化并不剧烈;而在图4(a)中,高阶衍射能量受到极大抑制,即随着网格线距与线径的缩小,中心点的能量会大大集中,使得高阶能量相应地减低。

根据电磁衍射机理,不锈钢织物的透光率与电磁屏蔽效能主要与网格中心衍射能量有关。如图2中b1～b6曲线所示,在透光率80%～100%内,此时网孔的高阶衍射已经受到了极大的抑制,这时线距的改变对于透光率的影响极为微弱,故在图2中表现出了陡然上升的趋势。相应地,在这一范围内的图3中曲线e1～e6可以看出,在屏蔽效能40～50 dB出现了陡降到平缓的变化,即线距的微弱变化会导致屏蔽效能的大幅度增加,这是由中心阶能量的集中带来的。同样地,在透光率0～20%内,图2中曲线a1～a6的陡降就是由于高阶衍射的影响过大,从而影响了成像质量,而在55～65 dB的屏蔽效能区间,线径在增加到一定程度时,由于此时高阶衍射的影响可忽略,中心阶能量集中,屏蔽效能会随着网孔的缩小快速提高至接近金属平板。

综上所述,当不锈钢织物线距较大时,其高阶衍射能量分布较为趋同,此时的结构参数变化对透光率的影响并不大,而当线距较小时,高阶衍射能量会出现明显地降低,此时线径与线距的变化会大幅影响透光率与屏蔽效能的呈现。因此,随着不锈钢织物结构参数趋于精细,即在保证透光率的情况下,将网格的结构参数尺寸等比缩小,可使得电磁波的高阶衍射能够得到抑制,从而使屏蔽效能更好,可见光成像质量更优。

1.5 不锈钢织物透光与电磁屏蔽性能测试与表征

根据1.2与1.3中理论分析结果,设计并制备线径为0.02～0.08 mm,线距为0.4～1.6 mm的三个不锈钢织物。三个样品的理论透过率为90%。

1.5.1 不锈钢织物透光性能测试与表征

本文采用如图5所示UV-Vis-NIR分光光度计对不锈钢织物样品进行透光率测试,测试波长为400～760 nm。测试结果如图6所示。

图5 UV-Vis-NIR分光光度计Fig.5 UV-Vis-NIR spectrophotometer

由图6可看出,三款不同结构参数但理论透光率相同的不锈钢织物,其透光率极为接近,约为86.25%。与理论计算结果相比,实验所测得的结果略微偏小。其主要原因是由于不锈钢织物结构使得光产生了衍射现象,检测设备无法收集到所有的高级次衍射光,从而使得实验检测数据小于理论值。

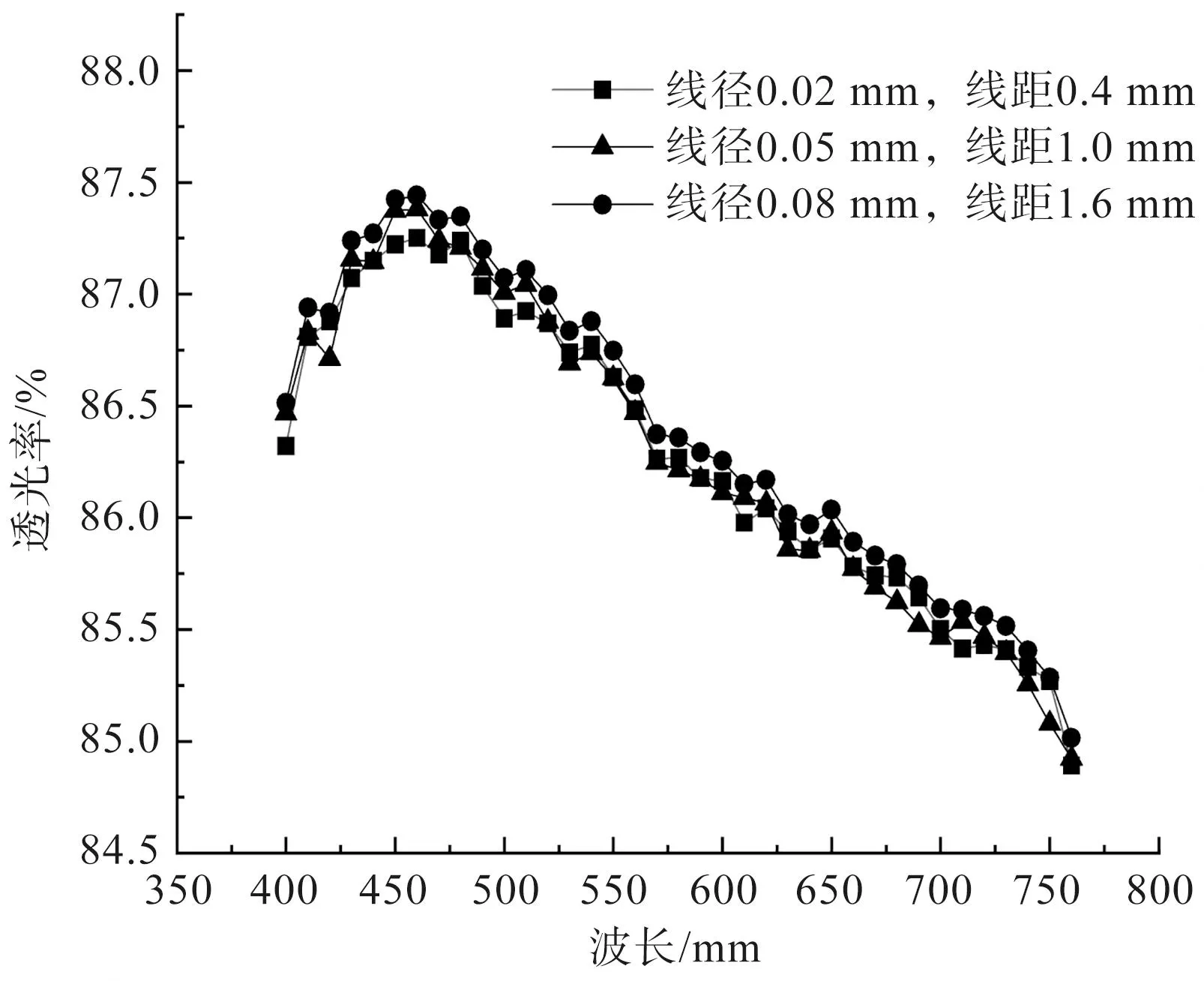
图6 不锈钢织物透光率测试结果Fig.6 Stainless steel fabric light transmission test results

1.5.2 不锈钢织物电磁屏蔽性能测试与表征

参考标准GB/T 30142—2013《平面型电磁屏蔽材料屏蔽效能测量方法》,采用法兰同轴法测试织物在30～1500 MHz频率内的电磁屏蔽效能。测试设备包含Keysight E5063A矢量网络分析仪、DR-S01法兰同轴屏蔽效能测试装置,如图7所示。测试结果如图8所示。

图7 法兰同轴测试装置Fig.7 Flange coaxial testing device

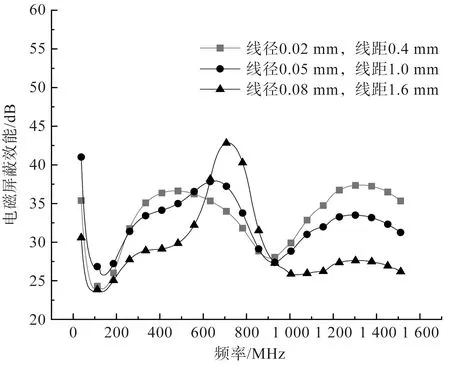
图8 不锈钢织物电磁屏蔽性能测试结果Fig.8 Test results of stainless steel fabrics’ electromagnetic shielding performance

由图8可知,三款不同结构参数的不锈钢织物的电磁屏蔽性能均在30～45 dB内,电磁屏蔽效能较好,但相比理论计算结果的40～50 dB存在一定差距。这是由于实际制备过程中存在的厚度不均匀、不锈钢丝接触点偏移、实测中的电磁泄漏等会对实测结果造成不可忽视的影响。

2 综合分析

基于上述对于透光性能与屏蔽效能影响的分析,本文利用正交试验设计方法,设计线径与线距两个因素,并根据1.2与1.3中分析,每个因素选取六个水平数,如表1所示。

其中透光性能通过式(1)计算得到,电磁屏蔽效能通过式(2)计算得到,综合性能引入TOPSIS评价方法。通过备选方案与理想值的距离分析综合性能的优劣,如评价因子Q[25],Q的值通过下式计算得到。

Q=TSU

(3)

式中:T为不锈钢织物的透光率,%;S为不锈钢织物的电磁屏蔽效能,dB;U为杂散光均匀度。

表1 不锈钢织物性能分析因素水平Tab.1 Performance analysis factor levels of stainless steel fabrics

根据表1分别对不同结构参数的不锈钢织物的透光性能、电磁屏蔽效能与综合性能三个指标进行直观分析,通过比较因子的每个水平均值的大小来评论此因子的水平好坏,并利用极差R,分析因素对指标影响的主次关系。指标分析结果如表2所示。

表2 指标分析结果Tab.2 Index analysis results

由表2极差分析结果可以看出,线距的透光性能极差R(0.49)大于线径(0.39),线距的屏蔽效能极差R(29.71)大于线径(13.04),线距的综合性能Q极差R(6 313.91)大于线径的(5 771.73)。因此,线距对不锈钢织物透光性能、屏蔽效能与综合性能影响最为密切的因素。对综合性能Q值分析时可发现,当透光率大于90%或小于50%时,Q值均较小,此时即便拥有较高的透光性能,但屏蔽效能的损失较大;而透光率在40%～60%内,Q值最大,但对于透光性能的下降较大;而透光率在70%～90%时,不锈钢织物的电磁屏蔽性能值达到 40～50 dB。即在保证90%及以上透光率的前提下,可设置不锈钢织物的线径在0.02～0.05 mm,线距在0.4～1.2 mm;而为了保证40 dB以上的屏蔽效能,可设置不锈钢织物的线径在0.02～1.2 mm,线距在0.2～1.0 mm。故为了不锈钢织物的高透光性能(大于90%)与强电磁屏蔽性能(大于40 dB)的兼容,可设置不锈钢织物的线径为0.02～0.05 mm,线距为0.4～1.0 mm。

3 结 论

本文以SUS316不锈钢织物为例,利用数值计算与机理分析相结合的方法,探究了结构参数(线径和线距)对透光和电磁屏蔽性能的影响,并引入TOPSIS评价体系,提出通过一种量化的方法以对比其综合性能优劣。主要结论如下:

1)线径和线距变化对不锈钢织物综合性能的影响存在的非线性规律。利用标量衍射理论,分析了高阶衍射能量变化对于不锈钢织物的透光率与电磁屏蔽效能的影响,解释了上述关系曲线中斜率急剧变化现象出现的原因。结果表明,在保证高透光率的情况下,不锈钢织物的结构参数同比越小,对总体性能的提升效果越好。

2)利用正交实验分析了线径与线距对不锈钢织物透光性能和电磁屏蔽性能的密切程度。通过极差分析可明确线距是对不锈钢织物透光性能、电磁屏蔽性能与综合性能影响最为密切的因素。

3)通过对评价因子Q的分析可知,当线径在0.02～0.05 mm、线距在0.4～1.0 mm时,不锈钢织物在90%透过率的前提下,其理论上能达到40～50 dB的屏蔽效能。

4)通过实验验证了理论分析结果,表明不锈钢织物的透光率实测值只有86%,存在4.4%的误差;电磁屏蔽测试结果为30～45 dB,数据误差在10%左右。