基于全局稳定性理论的e N 方法对高超声速有迎角锥背风流向涡转捩分析

陈 曦，涂国华，万兵兵，*，袁先旭，陈坚强，陈久芬

(1.空天飞行空气动力科学与技术全国重点实验室，绵阳 621000；2.中国空气动力研究与发展中心 超高速空气动力研究所，绵阳 621000)

0 引 言

高超声速边界层转捩会造成表面热流和摩阻剧烈变化，成为飞行器设计需要考虑的重要问题。针对诸如零迎角圆锥、平板外形等简单二维边界层的转捩现象，目前已有较充分的研究并取得了较大进展[1-5]。相较而言，虽然三维边界层转捩更能体现真实飞行的流动特征，但由于其流动结构复杂而研究难度大，相关研究尚处于起步阶段。典型的三维边界层转捩研究模型包括有攻角圆锥[6-13]、美澳HiFIRE-5的椭锥[14-20]、美国空军AFOSR的BOLT模型[21-22]以及中国空气动力研究与发展中心（CARDC）的升力体标模HyTRV[23-24]等。这些模型的共同点是由于周向压力梯度的存在，驱使流体从高压区向低压区汇聚，进而形成3种特征流动区域，即流向涡区（流线汇聚）、横流区和接触线区（流线发散）。下面重点介绍流向涡转捩研究现状。

流向涡转捩研究最早在风洞开展[25-26]，风洞实验主要关注转捩位置的参数影响规律，少量实验开展了扰动波的定量测量。由于缺乏空间场测量数据，难以判断流向涡的主导失稳模态。随着算法和计算机技术的发展，近年来涌现出不少涉及流向涡转捩的数值模拟结果。数值模拟可依赖动态模式分解（dynamic mode decomposition, DMD）技术[27]得到不同频率的扰动信息，通过傅里叶分析可得到流向涡转捩中扰动频谱、幅值等物理量的定量演化过程[22]。相比风洞实验和数值计算，稳定性分析可以更快速、更直接获得流向涡主导失稳模态。早期的流动稳定性分析忽略了流向涡的周向流动变化，而采用局部一维线性稳定性理论（linear stability theory, LST）分析当地位置点的流动稳定性特征。最早将流向涡的展向变化纳入考虑的是Choudhari等的工作[15]，他们将椭锥短轴流向涡稳定性问题归结为二维矩阵特征值问题（BiGlobal），发现BiGlobal结果与一维分析问题结果相差较大，于是他们得出结论：流向涡问题需要考虑展向流场变化。Choudhari等求解的是时间模式BiGlobal问题，不能描绘流向涡模态在空间上的失稳特征。Paredes等[17]开展了空间模式下的BiGlobal问题研究，发现流向涡存在对称和反对称模态，在低雷诺数条件下两者具有相似的性质，而在高雷诺情形下对称模态比反对称模态更不稳定。李晓虎等[28]根据模态形状函数分布特征将对称和反对称模态进一步细分为Y模态和Z模态，其中Y模态主要分布在流向涡肩部，而Z模态主要分布在流向涡柄部（stem region），此外Z模态频率、相速度和增长率等都较Y模态低。最近，Choudhari等[20]采用面推进抛物化稳定性方程（3D parabolized stability equations, PSE3D）研究了小迎角飞行工况下椭锥流向涡扰动演化问题，他们发现反对称模态最不稳定，其基于PSE3D（全局稳定性理论）的eN方法得到的N值在飞行试验转捩位置达到15左右。针对HyTRV升力体标模，流向涡结构主要存在于标模下表面中心区和上表面肩部区域。下表面中心流向涡结构类似于椭锥短轴上的流向涡，而上表面肩部流向涡是一种非对称的三维涡结构。Chen等[24]针对该非对称流向涡开展了稳定性分析，发现在流向涡肩部外缘区的失稳模态（称为外模态）占主导。

有迎角圆锥是工程常见的典型标模，但其背风流向涡转捩研究还相对较少。陈曦等[29]针对高超声速常规风洞工况下有迎角圆锥背风流向涡失稳开展了稳定性分析和直接数值模拟工作，基本流采用转捩场的平均流，研究发现反对称模态最不稳定，其N值在DNS转捩位置可达10左右。Li等[30]针对相同工况，以层流场开展了稳定性分析，进一步明确在上游反对称的Z模态占据主导地位，可能导致转捩提前发生。由于该模态分布主要集中在流向涡柄部的内剪切层区域，因此也被称为内模态。他们还发现流场中存在被流向涡修正的Mack（第二）模态不稳定性。随后他们还考察了背风中心线小突起粗糙元对流向涡稳定性的影响，发现外模态被抑制，流向涡转捩可能被延迟[31]。Paredes等[32]研究了迎角对钝锥背风面流向涡的影响，发现随着迎角从0°增大到5°，背风面中心线失稳位置逐渐前移，但由于与风洞实验转捩位置对应的N值都低于2，他们推测模态失稳前的非模态增长可能参与了转捩过程。最近，Zhang等[33]利用BiGlobal和PSE3D分析了飞行工况下有迎角钝锥流向涡失稳特性，发现内卷涡是其主导涡结构，导致内模态具有与外模态相当的失稳频率，与前人研究中外卷涡主导的结果不同；他们还发现由于冷壁效应，该内模态具有声辐射性质，而Mack模态最不稳定。Wang等[34]利用直接数值模拟和BiGlobal分析考察了壁温比对钝锥背风面流向涡转捩的影响，发现增加壁温比虽然可以抑制流向涡不稳定性，但却导致流向涡转捩提前，他们认为转捩提前的原因在于高壁温比促进了侧面横流不稳定性，后者影响了流向涡转捩进程。

综上所述，有迎角圆锥背风面流向涡失稳研究还不充分，特别是缺乏理论与实验的细致对比研究。本文将针对不同工况下的有迎角圆锥背风流向涡开展全局稳定性分析，分析流向涡不同模态的失稳机制，并结合风洞实验分析转捩N值。

1 风洞实验条件和结果

风洞实验是在CARDC口径1 m暂冲吹吸式高超声速风洞中进行，可通过选定喷管和控制总温总压参数获得所需来流马赫数和单位雷诺数，并配备快速送机机构，便于瞬时测热实验，详细介绍可参考文献[35]。实验模型为半锥角7°的圆锥模型，总长约800 mm，其中锥顶端采用可更换结构，头部半径rn=0.05、5 mm，见图1。图1还展示了迎角α0、直角坐标系（x为轴向，y指向背风中心线，z指向垂直于x-y平面方向）及相应的速度分量（U, V, W）、随体坐标系（ ξ,η,ζ）及相应的速度分量（Uξ,Vη,Wζ）和半锥角（ θ0）。模型共加工两套，一套是金属模型，用于脉动压力测量，采用8个高频脉动压力传感器（PCB，采样频率3 MHz，安装在同一条母线上，具体位置x=125、205、285、365、445、525、605、685 mm）；一套是非金属模型，由金属头部和聚四氟乙烯尾部组成，金属头部理论长度为165 mm，非金属段长度为635 mm，非金属段可用于红外热图测量，采用红外热像仪系统。红外测温技术可以在不破坏模型表面的情况下获得模型表面温度分布，然后根据层流到湍流的明显温升特点判断转捩位置或阵面。本文考察的风洞工况见表1。

表1 风洞实验工况Table 1 Wind tunnel experimental conditions

图1 研究模型、来流条件、直角坐标系和随体坐标系等示意图Fig.1 Sketch of the model, freestream conditions, the Cartesian coordinate system ( x, y, z )and the body-oriented coordinate system ( ξ, η, ζ )

利用红外热像仪测得模型表面温度随时间的变化，采用阶跃热流法[36]求得表面热流分布。在阶跃热流法中，假设模型表面热流变化为阶跃形式，据此可推得热流值Q如下：

其中， ∆Tw为壁温在 ∆t时间内的变化值， ρ1、c1和k1分别为模型材料的密度、比热和热传导系数。本文采用流动稳定段 ∆t=1 s的温升数据计算热流值。图2给出表1中3个工况下背风面热流分布。热流数值根据以往实验模型的物性参数标定，存在一定误差，但热流变化对物性参数并不敏感。若参考背风中心线热流分布，以热流开始快速抬升位置作为转捩起始位置，以热流峰值位置作为转捩终止位置，则3个工况下的转捩发生区（图2绿色带状区）分别为x∈(165mm,250mm) （ 工况1）、x∈(200mm,280mm)（工况2）和x∈(200mm,310mm)（工况3）。我们注意到转捩区长度大致在100 mm左右，远大于相近工况下的数值模拟结果[34]。这说明我们的转捩区划定偏保守，扰动的非线性效应在转捩区前期可能并不显著。图中还可看到，工况1和工况2的转捩阵面与工况3的转捩阵面明显不同，可能是由于流场结构的差异导致。从第3节中可见，工况1和工况2的背风面中心线附近流场在转捩位置附近还未发生明显卷曲，而工况3的流场已出现明显的流向涡结构。此外，还注意到工况2和工况3的转捩阵面并不对称，推测可能的因素有两个：一是模型安装存在微小的偏航角；二是表面因加工误差存在不均匀粗糙度。考虑到中心线附近转捩结果的局部对称性较好，而本文关注的流动正好集中在背风面中心线附近，因此该实验结果对本文的理论分析研究仍具有参考意义。

图2 红外试验测得的圆锥背风面转捩阵面（左列，虚线表示中心线）和对应的背风中心线热流值Q分布（右列）（a）工况1，（b）工况2，（c）工况3Fig.2 Infrared measurement of transition fronts (left) and axial variations of the wall heat flux in the leeward center lines (right), (a) Case 1，(b) Case 2，(c) Case 3

图3给出工况1不同流向站位处压力传感器测得的扰动功率谱。在x= 125 mm出现200 kHz左右高频扰动峰值，在x= 205 mm出现150 kHz左右的高频峰值，之后下游功率谱变为宽谱，没有明显的扰动峰值，表明转捩已经发生。

图3 工况1的功率谱Fig.3 PSD of Case 1

2 计算方法与分析理论

2.1 数值模拟方法

本文采用高精度数值模拟方法求解笛卡尔直角坐标系(x,y,z)下的Navier-Stokes方程，方程中空间黏性项采用四阶中心差分格式，对流项在经过Lax-Friedrichs通量分裂后采用三阶WENO差分格式；时间项采用三阶Runge-Kutta离散格式进行推进，推进的时间步长采用当地化CFL参数，这里设定为0.8。边界条件为：壁面采用无滑移、无渗透的等温条件，上边界采用来流条件，出口采用一阶外推法。

计算网格在流向、周向和法向分别布置501、301和301个点，并在近壁和头部附近加密。为了准确捕捉流向涡的周向流场变化，网格在背风流向涡附近也做了加密处理。网格分布特征如图4所示。为了验证网格无关性，针对工况2，补充计算一套不同网格，即法向和展向网格均增加到351个点。图5给出基于这两套网格的基本流流向涡结构，不同颜色曲线代表不同网格下的流向速度等值线，对比了x= 550 mm和x= 950 mm的流向涡结构。可以看出二者基本无差异，说明现有网格分辨率足够计算流向涡结构。

图4 网格分布特征（流向间隔5个点绘制，法向和展向网格均间隔2个点绘制）Fig.4 Computational mesh(For clarity, every fifth points in the axial direction and every second points in other two directions are plotted)

图5 工况2下两套网格的流向涡结构对比（流向速度等值线，间隔为0.1）Fig.5 Grid independent test of the laminar solution (axial velocity) for Case 2

2.2 全局稳定性理论及eN方法

全局稳定性理论有两种分析方法，分别是BiGlobal和PSE3D。BiGlobal是求解当地二维特征值问题的理论方法，相比LST方法，增加考虑了展向流动变化，可预示更复杂的涡流动失稳机制。PSE3D是面推进的三维抛物化稳定性方程方法，解决的是扰动空间演化问题，比直接数值模拟方法效率高且不失精度。基于全局稳定性的eN方法的基本理论框架是通过BiGlobal获得当地扰动模态；然后将其作为入口条件，利用PSE3D沿流向推进获得不同流向站位的扰动增长率；最后通过eN方法积分增长率，获得N值分布。下面具体介绍理论方法。

BiGlobal和PSE3D均要求基本流在流向是缓变的，这点在随体坐标系下是成立的，即基本流沿ξ方向（母线方向）变化缓慢。于是，下面均基于随体坐标系构建BiGlobal和PSE3D的方法体系。

对于BiGlobal方程，将流场分解成层流场加扰动场，其中扰动场基于平行流假设，其三维扰动形式为：

其中，q≡(ρ,u,v,w,T)T，代表时均场，为以温度脉动峰值归一化的扰动形状函数；ε表征扰动幅值大小，一般假设ε≪1；ω为扰动频率；待求的α实部为扰动波数，虚部负值为增长率；c.c.代表共轭。本文中，增长率和位置信息一般用有量纲来表示，而其他物理量均采用对应的来流值无量纲化。将上式代入(ξ,η,ζ)坐标系下的Navier-Stokes方程，通过线性处理（只保留一阶小量）可得空间BiGlobal方程如下：

其中，A0、A1和A2是包含层流场信息的算子，具体形式见文献[24]。

针对该方程，采用四阶有限差分离散。展向计算域根据流场特征选取为 0≤ϕ≤23 ，其中 0代表背风中心线，而另一个展向边界（ ϕ=23）远离流向涡结构；法向外边界距离壁面17 mm左右，同样远离流向涡结构。经过计算表明，进一步扩大计算域并不影响分析结果。在背风中心线处采用对称或反对称边界条件，在其他边界处均为在计算过程中，分别采用对称和反对称条件来得到对称模态和反对称模态。对于工况1和工况2，我们发现反对称模态和对称模态性质相近（主频、增长率、相速度和形状函数等性质），但对称模态更不稳定，因此本文展示的结果均为采用对称条件得到的对称模态结果；对于工况3，外模态对中心线处边界条件并不敏感，而内模态则在反对称条件下更不稳定，因此展示了对称外模态和反对称内模态的结果。根据流场结构和不稳定性性质的不同分别采用从100到201和从100到300不等的网格点。方程采用隐式Arnoldi方法[37]进行迭代求解，当找到一个物理不稳定模态时，可进一步采用牛顿迭代法计算该模态在频率或流向位置连续变化时的特征值。牛顿迭代方法[33, 38]可写作如下形式：

其中下标j代表迭代步数，Ξ、F和JF可表示为：

f1是离散的全局稳定性方程（与式（3）一致），可写作如下矩阵形式：

f2是归一化条件：

当F的模（离散形式下有）小于1×10-7时，迭代停止，即可得到特征值。

对于PSE3D方程，考虑非平行效应影响，将流场作如下分解：

同样，代入Navier-Stokes方程后，基于层流场和扰动形状函数均沿流向ξ缓变，仅保留其一阶流向导数项，并忽略非线性项O(ε2)，可得PSE3D方程，形式如下：

式中L和M为包含层流场信息的微分算子，具体形式见文献[24]。

该方程的离散方式与BiGlobal方程一致，求解方法采用一阶隐式欧拉格式的流向推进方式，用来推进的入口条件由BiGlobal给出。为保证形状函数沿流向ξ缓变，需在每步迭代α使得：

其中：

当前后两步的波数差别的绝对值小于1×10-5时迭代收敛。得到α后，即可积分其虚部（负值为增长率）得到N值：

其中，ξ0代表扰动中性失稳（即BiGlobal预测的扰动增长率为零）位置。

3 结果与分析

图6给出3个工况下圆锥背风区流向速度剖面云图，可以看出圆锥背风中心线附近都存在流向涡结构，且其强度随雷诺数或迎角的增大而增强。下面分别针对这3个工况的流向涡开展全局稳定性分析。

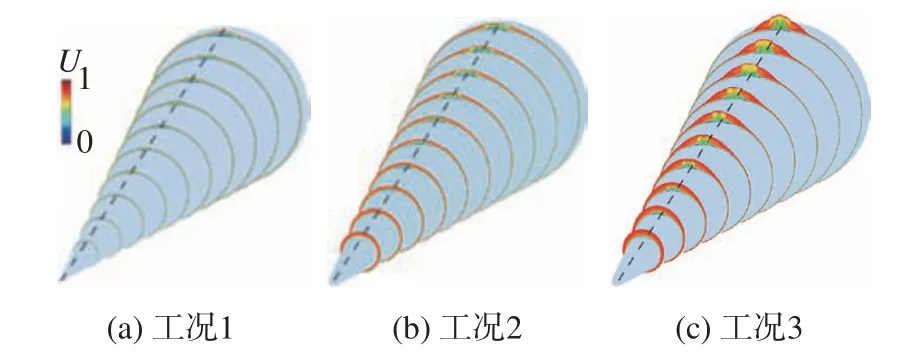
图6 3个工况的背风面流向涡结构沿流向的演化（云图代表流向速度，虚线为背风中心线位置）Fig.6 Axial evolutions of leeward vortices in Case 1, Case 2 and Case 3（Dashed lines represent the leeward centerlines）

3.1 工况1

工况1为小迎角尖锥流动，其背风流向涡结构并不显著，如图7所示。背风对称面附近的基本流在约401 mm之前只能看到微微隆起，推测上游主要由修正的二维边界层不稳定性主导。为了验证这一推测，对x= 401 mm之前的流向涡进行全局稳定性分析。

图7 工况1在x = 101、401 mm流向站位处的流向速度分布Fig.7 Axial velocity profiles in y-z planes at x = 101 mm and x = 401 mm for Case 1

之前的工作以及研究[17]表明反对称模态与对称模态性质相似，但后者更不稳定。图8为x= 101 mm、f= 190 kHz的对称模态特征谱，可见特征谱上只有一个不稳定模态。计算表明上游流场只存在这一个不稳定模态，该模态随流向站位和频率的变化关系如图9所示。图9（a）显示，模态的温度脉动形状函数上下双层结构，且其主频随流向位置向下游发展而逐渐减小，属于典型的Mack模态特征，因此可判断该模态属于Mack模态。图9（a）的理论预示结果与图3风洞实验频谱在转捩之前随流向站位的变化规律一致。此外，从图9（b）可以看出，Mack模态的无量纲相速度集中在0.85～0.95，且随频率增加先减小后缓慢增加。这些结果与二维情形一致。在401 mm处，除了主Mack模态外（绿色五角星），还出现高频不稳定模态（蓝色和浅蓝色五角星）。从图9给出的形状函数分布看，高频不稳定模态同样也属于Mack模态。

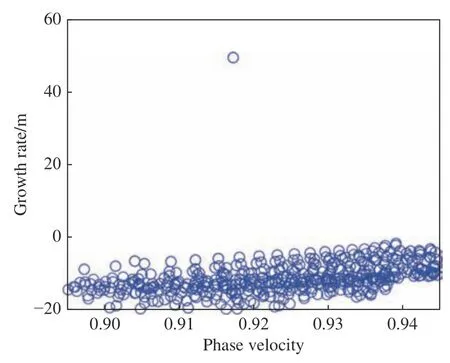
图8 工况1在x = 101 mm流向站位处频率为190 kHz的特征谱Fig.8 Eigenvalue spectrum for frequency 190 kHz at x = 101 mm in Case 1

图9 工况1在6个流向站位处的不稳定模态分布，云图表示x = 401 mm处的前两阶模态（最不稳定频率）的温度形状函数（实部）分布Fig.9 Variations of (a) growth rates and (b) phase velocities with frequency at six axial stations.Insets are the temperature disturbance(real part) distributions of the two most unstable modes in y-z planes

利用PSE3D方法对上述主导模态的增长率进行积分获得N值分布，如图10所示，图中不同颜色曲线代表不同频率的N值。可以看出，频率越低，N值越大，在x= 500 mm处，最大N值为5左右。与图2（a）的实验转捩位置相比可知，转捩区对应的N值约在2～2.5之间。此外，高频扰动在x= 400 mm后开始重新增长，表明流向涡不稳定性开始出现。

图10 工况1不同频率流向涡失稳模态的N值（绿色区域表示实验测量的转捩位置范围）Fig.10 Axial variations of N-factors of unstable modes for the leeward vortex with several frequencies in Case 1（The green zone represents the experimental measured transition zone）

3.2 工况2

相比工况1，工况2的迎角仍为2°，但模型钝度和来流雷诺数均有增加。图11展示了4个流向站位处的背风中心线附近的流向速度云图，可见在300 mm前流场都保持较好的二维特征，300 mm处流场在背风中心线附近有近似均匀的隆起（即低速区），该低速区在350 mm处出现明显的周向扭曲，并在400 mm处出现流向涡形态的卷曲。工况2的基本流在300 mm之前与工况1的基本流定性一致，之后则呈现更复杂的流动特征，这是因为头部钝度和来流雷诺数较工况1有显著增加的缘故。

图11 工况2在x = 100、300、350、400 mm流向站位处的流向速度层流场Fig.11 Axial velocity profiles in y-z planes in Case 2 at x = 100, 300, 350, 400 mm

基本流在x= 300 mm前后的差异直接导致流动不稳定性在300 mm前后呈现迥异的特征，如图12所示。从图12（a）可以看出，在x= 300 mm之前，Mack模态为唯一不稳定性；随着流向站位向下游变化，其主频从350 kHz递减至100 kHz，其最大增长率则先增后减。这与工况1中的最大增长率沿流向逐渐递减不同。此外在上游工况2中Mack模态明显比工况1中的稳定，这些差异主要源自钝度影响：更大的钝度抑制了Mack模态的增长。

图12 不同流向站位的不稳定模态增长率随频率的变化：（a） x = 100 ~300 mm； （b）x = 350 mm；（c） x = 400 mm.五角形代表Mack模态，圆圈代表流向涡外模态和内模态；（d） x = 400 mm处最不稳外模态形状函数（温度脉动实部）分布； (e) x=400 mm处最不稳内模态的形状函数（温度脉动实部）分布Fig.12 Variations of the growth rate with frequency at (a) x = 100 ~300 mm; (b) x = 350 mm; (c) x = 400 mm.(d) and (e) are, respectively,the temperature disturbance (real part) distributions of the most unstable inner and outer modes in y-z planes at x = 400 mm(Pentagon: Mack modes; Circle: inner and outer modes of leeward vortex)

在x= 350 mm处，Mack模态仍占据主导地位，但还出现了多个流向涡模态，如图12（b）所示。其中，在Mack模态频带附近出现两支外模态（扰动集中在外剪切层），而在低频区出现两支内模态（扰动集中在内剪切层）。外模态的失稳频带非常宽，其中一支外模态（红色符号）在100 kHz附近还呈现三维Mack模态特征。随着基本流在下游进一步卷曲，流向涡模态在x= 400 mm成为主导失稳模态，见图12（c）。图12（d、e）展示了x= 400 mm处最不稳定流向涡外模态和内模态的形状函数分布，可见外模态分布在流向涡肩部处的外剪切层，而内模态位于流向涡柄部内剪切层，与之前研究结果[30]一致。

由于流向涡内外模态远在实验观察到的转捩位置之后才逐渐成为主导失稳模态，因此它们不大可能是转捩的主导因素。在转捩位置之前只有Mack模态，于是在图13只给出了Mack模态的N值变化曲线。与工况1结果相似，扰动频率越低，失稳区越靠后而N最大值越大。与实验转捩位置（见图2（b））对应的最不稳定频率约为120～160 kHz，转捩区对应的N值约在0.4～2.5之间。

3.3 工况3

工况3比工况2的迎角增加2°，迎角的增加导致周向压力梯度增大，进而在圆锥背风面产生更显著的流向涡结构，如图14所示。流向涡结构早在x= 180 mm处就已显现，在x= 250 mm处已发展成熟。

图14 工况3在x = 120、180、250、350 mm流向站位处的流向速度层流场Fig.14 Axial velocity profiles in y-z planes in Case 3 at x = 120, 180, 250, 350 mm

图15展示了6个流向站位处的不稳定模态扰动增长率分布。可以看出，上游Mack模态依然为主导不稳定性（图15（a）），其主频是工况2中相同位置处Mack主频的一半左右，这是因为工况3迎角增加导致背风面边界层厚度增大的缘故。随着边界层的快速卷曲，低频流向涡内模态（蓝色和绿色圆圈）率先出现（图15（b））。然后在180 mm处成为主导不稳定性（图15（c）），而Mack模态的最大增长率和主频皆沿下游单调下降，直到在200 mm之后完全消失（图15（d））。在200 mm处，失稳频率范围达20～350 kHz的外模态（红色圆圈）出现，并最终在下游成为主导模态（图15（e、f））。

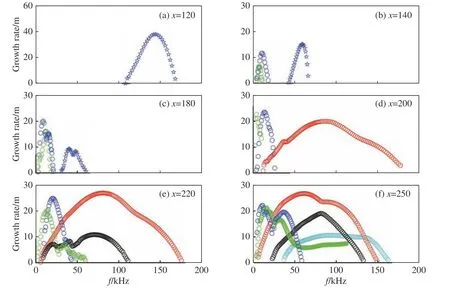
图15 工况3不同流向站位处的不稳定模态扰动增长率分布（五角形代表Mack模态，圆圈代表流向涡外模态和内模态）Fig.15 Variations of growth rate with frequency for unstable modes in Case 3 at x= 120, 140, 180, 200, 220, 250 mm(Pentagon: Mack modes; Circle: inner and outer modes of leeward vortex)

图16给出了x= 250 mm处流向涡失稳主导模态的形状函数分布，图16（a、b）表示图15中前两阶最不稳定的外模态（红色圆圈和黑色圆圈），图16（c、d）表示图15中前两阶最不稳定的内模态（蓝色圆圈和绿色圆圈）。可见外模态分布在流向涡肩部外缘，而内模态分布在流向涡柄部。

图16 工况3下x = 250 mm处前四阶不稳定模态的温度（实部）形状函数分布（云图）：（a、b）前两阶外模态；（c、d）前两阶内模态.频率为图14（f）中各模态最不稳定频率，线图为流向速度等值线图，间隔为0.1Fig.16 Temperature disturbance (real part) distributions of the two most unstable (a, b) outer and (c, d) inner modes in y-z planes at x=250 mm overlaid by the axial velocity contour lines

图17给出了不同频率模态扰动的N值演化曲线，可见Mack模态在上游率先失稳，这与前两个工况相似，但最大N值均难以超过2；而反对称内模态在200 mm后迅速失稳并很快成为主导不稳定性，与风洞实验观察到转捩位置附近（图2（c））对应的最不稳定频率约为30 kHz，转捩区对应的N值约在1.8～6之间。

图17 工况3不同频率流向涡失稳模态的N值（实线：反对称内模态；虚线：对称外模态；点划线：对称Mack模态.绿色区域表示实验测量的转捩位置范围）Fig.17 Axial variations of N-factors of unstable modes for leeward vortex with several frequencies in Case 3 (Solid lines:inner modes; dashed lines: outer modes; solid dotted lines: Mack modes.The green zone represents the experimental measured transition zone)

4 结 论

本文针对高超声速有迎角圆锥的背风流向涡，利用BiGlobal和PSE3D方法开展了全局稳定性与转捩分析，并结合风洞实验研究了流向涡转捩N值，进一步认识了流向涡转捩机制，主要结论如下：

1） 在流向涡较弱的阶段，Mack模态为主导不稳定性；当流场出现明显周向卷曲时，流向涡失稳模态开始出现，并随着卷曲的加强而逐渐成为主导模态，同时Mack模态逐渐消失。流向涡模态可按扰动分布分为外模态和内模态，其中外模态具有较高主频和相速度，内模态主频和相速度相对较低。

2） 结合风洞实验测量的转捩位置，对于2°小迎角圆锥，流向涡较弱，基于全局稳定性得到的转捩N值不到3；而对于4°迎角圆锥，流向涡相对较强，转捩完成时的N值能达到6左右。

对于本文选择的工况与研究模型，实验中转捩发生位置对应的模态失稳的N值都比较小，说明转捩不全由模态失稳贡献完成的。模态失稳扰动需要通过风洞中来流扰动的激励和演化而来，期间扰动以非模态形式存在，可能经历非模态增长。前人研究[39]表明非模态增长是引起转捩的重要机制之一，因此下一步将开展非模态分析，以确定非模态增长机制是否可能在上述工况的背风区转捩中扮演重要角色。

致谢：本文用到的风洞实验数据得到了中国空气动力研究与发展中心徐洋工程师等的帮助，在此表示感谢！