考虑移动式储能调度的配电网灾后多源协同孤岛运行策略

2024-03-07王育飞李可铭于艾清

电力系统自动化 2024年3期

王育飞，李可铭，2，薛花，于艾清，米阳

（1.上海电力大学电气工程学院，上海市 200090；2.国网上海市电力公司金山供电公司，上海市 201500）

0 引言

近年来，自然灾害等极端事件的发生愈加频繁，而配电系统作为电力系统的末端，因其较为脆弱的特点更易受到破坏，从而造成大面积停电现象［1］。电力作为国民经济命脉，是关系到国计民生的重要能源产品，电力系统的安全稳定运行是维持社会生产秩序的前提［2］。因此，利用各类恢复资源为灾后配电网及时提供能量支撑，提升配电网应对极端事件的弹性能力具有重要意义。

随着各类同步发电机、风光储系统等分布式电源（distributed generator，DG）的快速发展与普及应用，国内外学者对利用DG 进行配电网灾后孤岛运行也开展了广泛研究。文献［3-4］考虑孤岛划分与网络重构的相互配合，利用DG 与主网的协调控制对配电网进行灾后恢复。文献［5］计及新能源与负荷的动态不确定性对配电网恢复的影响，配合动态孤岛划分手段进一步提高配电网灾后恢复能力。文献［6］提出一种考虑主动孤岛和远程控制开关的综合恢复策略，在多时段孤岛运行中实现快速故障隔离及提高抵御极端事件影响的能力。然而，以上研究在孤岛运行层面仅进行了孤岛划分，且多以单源单孤岛的形式或提前设定好孤岛个数的形式进行孤岛划分，孤岛数目无法动态优化，多源协同能力未能充分发挥。

此外，移动式储能系统（mobile energy storage system，MESS）应用技术的发展也为配电网灾后恢复提供了新的手段。目前，MESS 除在闲置情况下提供削峰填谷［7］、降损调压［8］等服务以外，主要用于应急供电与负荷恢复。文献［9］考虑交通路网下的MESS 调度，建立了有源配电网灾后均衡恢复模型，实现了MESS 与本地电源为同等权重的负荷进行公平、均衡供电。文献［10］提出了端对端交易模式下的MESS 电能共享机制，通过优化MESS 的充放电功率以实现灾后配电系统的韧性提升。文献［11］创新性地提出可分离式移动储能的概念，将传统调度模式进行拓展延伸，使MESS 更加灵活地为灾后电网提供多时段的有功能量补充。文献［12］提出了混合移动式储能的使用方法，旨在调度其为灾后电、冷负荷协同供能。然而，实际交通网络作为MESS 的行驶载体，上述研究在路-电耦合方面未进行深入研究，行驶过程仅做了简化处理。

交通流量作为路网交通状况的一种衡量标准，移动资源的路径规划需要充分考虑交通流量产生的影响。文献［13］考虑实时交通数据及通信网络的影响，提出一种考虑MESS 辅助的多时段供电恢复策略。文献［14］将交通流量的影响直接量化为已知的交通道路通行时间，提出一种考虑MESS 与抢修队交替配合的电网修复策略。以上研究计及了实时交通情况对移动资源路径规划的影响，但多以预先设定好的全时段交通流量信息为基础，未能通过详细模型来刻画交通流量的动态变化。因此，无法充分考虑实际路况信息对MESS 现实调度产生的影响，所制定的调度策略脱离了交通层面的实际情况，导致调度结果过于理想。

基于现有研究的不足，文中提出一种考虑交通路网下MESS 调度的配电网灾后多源协同孤岛运行策略，充分考虑了交通流量的不确定性对MESS调度过程的影响。同时，将提高电能分配能力的多源协同手段考虑在内，并基于两阶段优化框架完成决策。算例验证表明，所提策略不仅可以在路-电耦合背景下为MESS 规划出参与灾后负荷恢复的最优路径，而且可以充分发挥多源协同能力，实现电能的最优分配和转移，有效提升灾后配电网的弹性水平。

1 考虑MESS 调度的配电网灾后多源协同孤岛运行框架与建模

1.1 路-电耦合背景下配电网灾后多源协同孤岛运行框架

随着电力系统与交通系统的耦合关系日益紧密，两系统均已具备信息互联互通的能力［15］。当极端事件发生后，引发的断线故障会将配电网分解为多块区域，交通路网的路段也会因极端事件的发生受到一定的破坏，进而影响到交通流量的分布。针对配电网的灾后恢复问题，除利用配电网本地的各DG 进行孤岛运行外，针对不存在本地DG 供电路径的失电孤岛区域，可选择移动类的电源资源（如MESS）进行辅助供电。

MESS 是连接交通路网与配电网的耦合设备，在制定调度策略时无法脱离实际交通背景单独制定，研究MESS 在路-电双网下的灾后调度对提升负荷恢复效果、提高与DG 间的协同运行能力具有重要意义。为此，文中提出了路-电耦合背景下考虑MESS 调度的配电网灾后多源协同孤岛运行框架，如图1 所示。

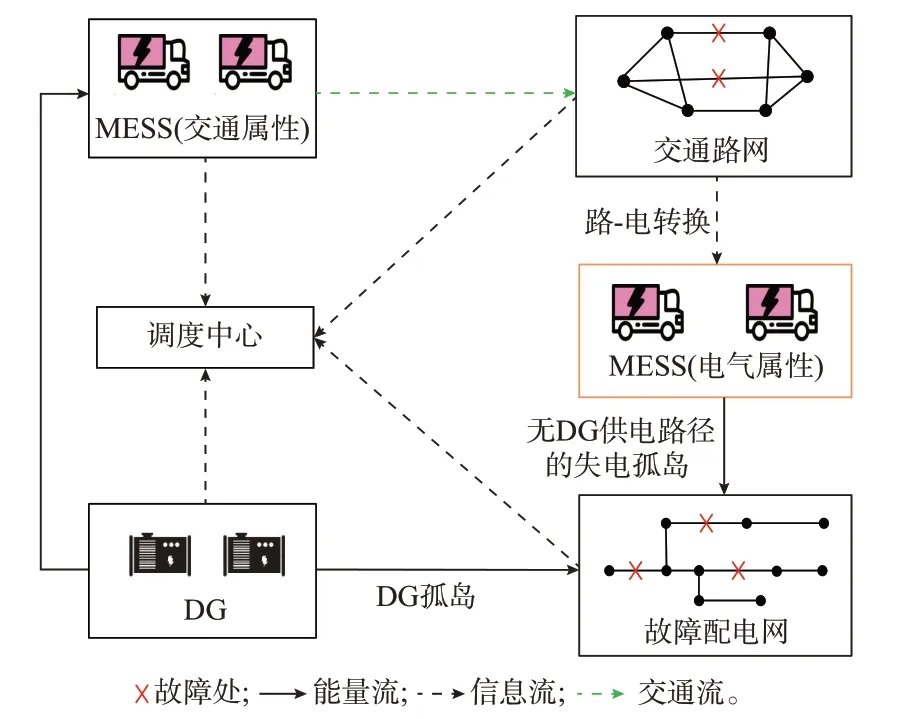
图1 路-电耦合背景下考虑MESS 调度的灾后运行框架Fig.1 Post-disaster operation framework considering MESS dispatching in the background of traffic-grid coupling

基于所建立的灾后运行框架，文中提出一种考虑MESS 调度的配电网灾后恢复策略。首先，调度中心根据对极端事件的评估结果，得到配电网和交通路网的受灾信息，再根据断线情况将受灾的配电网进行区域划分，明确需通过调度MESS 进行供电支撑的失电孤岛区域以及可通过DG 供电的区域。然后，针对MESS 供电的失电孤岛区域，基于路-电耦合特性决策出MESS 的最优调度路径，以实现对该区域内负荷电能的及时补充；针对可通过DG 供电的区域，为实现有限电能资源的优化分配并提高多源协同能力，将多源孤岛融合手段［16-17］纳入孤岛运行决策中。最后，通过各个电源间的协同配合，尽可能提高灾后配电网的负荷恢复效益。

1.2 路-电耦合背景下配电网灾后多源协同孤岛运行建模

1.2.1 MESS 行驶时间模型

调度MESS 进行供电恢复时，需要考虑实际交通网络对路径规划的影响，并在此基础上选取行驶时间最短的路径。文中采用适合中国道路交通情况的回归路阻函数模型［18］，以求解MESS 在各路段各种交通流量情况下的行驶时间，如式（1）所示。

式中：τij为车辆通过路段ij的行驶时间；βij，mv和βij，nmv分别为路段ij上机动车（含以汽车为载体的MESS）和非机动车的交通流量；βij，mv，max和βij，nmv，max分别为路段ij上机动车和非机动车的最大交通流量，即实际通行能力；Lij为路段ij的长度；vij，0为车辆在路段ij上的零流速度；k1和k2为回归参数，对应取值与路段类型有关，可通过最大似然估计法获得［19］。

为获得各个路段中交通流量的动态变化信息，所采用的流量预测模型应尽可能刻画出交通流的传播特性，以提高路径规划决策的适用性。差分Lighthill-Whitham-Richards（LWR）方程［20］可以用来描述车流速度、密度与流量的动态关系，而元胞传输模型［21］可作为差分LWR 方程的离散时间近似，并将交通路网中的各个路段转化为若干个元胞，元胞具有长度和车流方向两种属性，每个元胞都能反映交通流的传播特性。因此，可将元胞传输模型作为交通路段流量预测的基础。

由于车辆行驶时间取决于所选路径中各路段的交通流量，将路段转化为元胞之后，可将所有元胞内的机动车与非机动车交通流量总和最小作为流量预测模型的目标函数，其效果等价于车辆行驶时间最短［21］。具体的流量预测模型如下：

式中：Ttr为交通网中的时间集合；C为所有元胞组成的集合；A为两类车辆（机动车与非机动车）组成的集合；βc，a，t为t时刻元胞c中第a类车辆的流量预测值。

式中；ρ（c，d），a，t为t时刻从元胞c流向元胞d的第a类车辆的流量预测值；βc，a，max为任意时刻元胞c中第a类车辆的流量上限；π（c）和δ（c）分别为元胞c的上、下游元胞集合。式（3）表示每个元胞的车流量平衡约束。

式中；Qc，max和Nc，max分别为任意时刻可从元胞c流入流出的最大车流量和可存储在元胞c的最大车流量；γc为元胞c的堵塞系数。式（4）表示从元胞c流出的流量应满足的约束；式（5）表示流入元胞c的流量应满足的约束，其中表示元胞c出现交通拥堵时剩余的可占流量。

式中；βc，a，0为初始时刻元胞c中第a类车辆的流量值；ρ（c，d），a，0为初始时刻元胞c流向元胞d的第a类车辆的流量值。式（6）表示每个元胞的初始流量和每条元胞连线上的初始传输流量。

根据流量预测模型的结果，可将式（1）中的各变量替换成元胞变量，各个变量的含义由路段中的属性转化为元胞的属性。因此，在t时刻通过各个元胞的行驶时间τc，t均可由下式计算得到：

式中：Lc为元胞c的长度；vc，0为车辆在元胞c上的零流速度。

得到通过各元胞的行驶时间后，首先，基于配电网节点与交通网节点的耦合关系，利用Floyd 算法搜索MESS 从任意配电网出发节点到任意配电网目标节点所需行驶时间最短的路径，同时生成组成该路径的各个路段（元胞）。然后，将t时刻任意两节点间的最短行驶时间作为元素，构建t时刻的NN阶调度时间矩阵Ot，其中，NN为配电网节点个数。由于MESS 可能在整个配电网故障恢复期间进行多次调度，故在每一次调度的决策时刻都需要对流量预测模型进行重新求解，以实现交通流量和调度计划的滚动更新。

1.2.2 孤岛运行模型

为协调进行失电孤岛区域与含DG 区域的负荷恢复，本文在路-电耦合背景下，建立了考虑MESS调度的配电网灾后多源协同孤岛运行模型。

1）目标函数

为尽可能降低配电网灾后孤岛运行期间负荷的停电损失，考虑各类负荷的重要性，以加权切负荷量最小作为优化目标，即加权负荷恢复量最大。

式中：Tres为恢复过程的时间集合；N为配电网节点集合；ωi为节点i的负荷权重系数；Pdem，i，t和Pres，i，t分别为t时刻节点i的有功负荷需求量和恢复量。

2）约束条件

（1）负荷恢复约束

负荷恢复时，应保证负荷在需求量的限制范围内进行恢复。

式中：Qdem，i，t和Qres，i，t分别为t时刻节点i的无功负荷需求量和恢复量；xi，t为表示t时刻节点i的负荷是否投运的0-1 变量，投运则为1，否则为0。

（2）MESS 充放电管理约束

MESS 的充放电管理主要考虑MESS 的充放电特性以及MESS 在运行时对能量状态（state of energy，SOE）范围的要求。此外，MESS 在行驶过程中也会产生电能损耗，这会对MESS 到达目标点时的SOE 产生影响［22］。第m个MESS 通过元胞c时产生的电能损耗ΔEm，c如式（10）所示。

式中：σc为表示MESS 是否通过元胞c的0-1 变量，通过则为1，否则为0；vc为MESS 通过元胞c时的速度。

结合电能损耗ΔEm，c以及充放电状态与接入位置的耦合关系，MESS 的充放电管理约束如下：

式中：Ct为当前时间尺度内MESS 经过的元胞集合；Pch，m，t和Pdch，m，t分别为t时刻第m个MESS 的充电和放电功率；Sch，m，t和Sdch，m，t分别为t时刻第m个MESS的充电和放电状态；αm，i，t为表示t时刻第m个MESS是否接入节点i的0-1 变量，接入则为1，否则为0；Em，t为t时刻第m个MESS 的剩余容量；Pm，max为第m个MESS 的最大充放电功率；ηch，m和ηdch，m分别为第m个MESS 的充电和放电效率；Hm，max和Hm，min分别为第m个MESS 的荷电状态上、下限；Em，rat为第m个MESS 的额定容量；Qm，t为t时刻第m个MESS 的无功出力，Qm，max为其无功出力上限。

（3）计及行驶时间的MESS 接入点约束

调度MESS 时，除了需要满足接入点可容纳的MESS 个数限制外，还需确保MESS 由一节点调度到另一节点时至少需要花费时长为ζ的行驶时间。ζ为两点间的行驶时间，任意两节点间的行驶时间均由1.2.1 节提出的方法确定。此外，文中假设MESS 调度至目标点后，其安装时间忽略不计。

式中：ΩMES为MESS 的集合。

（4）交通路网与配电网的灾后约束

极端事件发生后，交通路网与配电网均受到一定程度的破坏，文中暂不考虑交通道路与配电线路的抢修工作。因此，灾后交通路网中受损路段的通行时间应定义为无穷大，受损配电线路始终断开。

式中：ΩFR为灾后交通路网中因受损而无法通行的路段集合；ΩFD为灾后配电网中受损的线路集合；M为一很大的正数；τij，t为t时刻车辆通过路段ij的行驶时间；zij，t为t时刻配电线路ij的开合状态，闭合为1，否则为0。

（5）计及多源孤岛融合的配电网拓扑约束

极端事件发生后，可通过孤岛划分手段对电能资源进行分配，以提高负荷恢复总效益。相较于传统孤岛划分方法中的单源单孤岛或将孤岛个数设置为提前预选好的主电源根节点的个数［5］，文中将孤岛个数动态优化的多源孤岛融合手段纳入孤岛运行决策中，通过优化孤岛划分后的拓扑实现电源出力与岛内负荷更好地匹配。

首先，需要保证生成的孤岛中不存在环路，而广泛应用的生成树约束会存在生成环路的可能。因此，文中利用断线解环［23］思想对该问题进行处理：

式中：R为所有环路组成的集合，可利用遍历图的方法获得；Rk为所选环路；|Rk|为组成所选环路的支路个数。

以保证孤岛的辐射状和连通性为基础，再将多源孤岛融合的判断引入拓扑约束当中，从而实现孤岛个数的动态优化：

式中：E为配电线路组成的集合；ΩADG为各电源节点组成的集合；λi，t为表示t时刻电源节点i是否为孤岛的主电源根节点的0-1 变量，若为1 则表示以电源节点i为主电源根节点的孤岛存在，否则为0。式（16）通过引入主电源根节点的表征变量，采用对其求和的方式替换了节点-边的数目关系中固定的根节点个数（电源个数），实现了孤岛主电源根节点的动态选择与孤岛范围的动态融合。

另外，还需要对λi，t的存在性进行约束：

式中：Fij，t为t时刻配电线路ij的虚拟潮流值；Di为虚拟负荷值。式（17）和式（18）通过用虚拟潮流的取值来完成对λi，t的耦合。根据大M法，当电源节点i为孤岛的主电源根节点时，虚拟潮流不受约束；反之，虚拟潮流将受Di的限制。

（6）其他约束

此外，孤岛运行模型还包括了配电网潮流和电压的安全约束、潮流平衡约束、DG 的出力范围约束等常规约束，具体见文献［24-25］。

2 考虑MESS 调度的配电网灾后多源协同孤岛运行策略

2.1 基于两阶段优化框架的孤岛运行决策流程

参考文献［26］的优化思路，本文基于两阶段优化框架制定了路-电耦合背景下考虑MESS 调度的配电网灾后多源协同孤岛运行决策流程，如图2 所示。两阶段优化框架的介绍以及采用该框架进行决策的必要性见附录A。

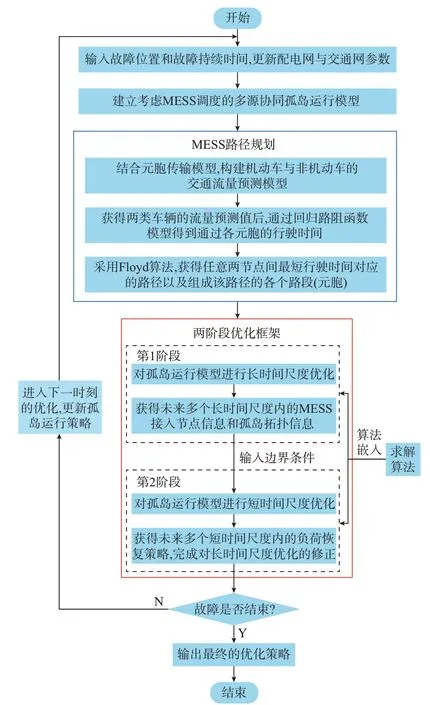
图2 孤岛运行决策流程图Fig.2 Flow chart of decision-making for islanding operation

2.2 求解算法

本文基于两阶段优化框架所建的长/短时间尺度孤岛运行模型均属于混合整数规划模型，且具有整数变量较多、高维且存在非线性等特征。因此，可选取智能优化算法进行求解。文中采用改进的免疫克隆选择算法（immune clonal selection algorithm，ICSA）进行模型求解［27-28］。

传统ICSA 模拟了免疫系统的克隆选择原理，因免疫系统具有多样性机制，ICSA 也具有一定的全局寻优能力。然而，传统的ICSA 在克隆选择时仅进行了抗体-抗原间的亲和力交流，未考虑抗体之间的亲和力。这种克隆操作会导致种群中出现大量相同或者相似的抗体，使得后期的选择和克隆操作中存在不必要的重复操作，同时种群多样性也会趋于贫化，从而影响算法的收敛和稳定，甚至使算法最终陷入局部最优。

针对传统ICSA 中因克隆选择操作未考虑抗体间亲和力从而导致的算法稳定性问题，文中利用文献［27］提出的抗体间亲和力模型对该问题加以解决：

式中：K（i）为第i个抗体的抗体间亲和力；θ和ε分别为被克隆的抗体个数以及未被克隆的抗体个数；di，j为抗体i和j之间的欧氏距离。

算法基本流程如附录B 图B1 所示。

3 算例分析

3.1 仿真算例

选取IEEE 33 节点有源配电网进行仿真分析，网络参考电压为12.66 kV，配电网共有32 条支路和5 个联络线开关，线路、负荷参数及网络初始拓扑见文献［17］；节点10、18、26 处接入3 个可控DG，其参数见附录B 表B1，暂不考虑具有不确定性的风、光等不可控DG 的参与；配电网中的负荷按重要程度分为一级负荷、二级负荷和三级负荷，权重系数分别取5、1 和0.2，负荷曲线见附录B 图B2；同时，在节点33 处停放两辆等待调度命令且处于满电状态的MESS，用于对灾后配电网的补充恢复，其参数［9］见附录B 表B1。

假设08：00 开始发生了极端灾害，除上级主网与配电网间发生中断，还造成了其余多线故障（线路1-2、2-3、7-8、16-17、27-28 以及联络线开关24-28），故障恢复时间持续9 h。结合故障断线情况，可先利用并查集方法找出无法通过DG 供电的失电孤岛区域，如图3 所示。

图3 灾后配电网区域划分Fig.3 Regional division of post-disaster distribution network

选取29 节点交通路网以完成对配电网的耦合，其拓扑及耦合关系见文献［8］，并假设交通节点7 与20、8 与15 之间的路段因损坏而无法通行。首先，将交通路网的路段属性转化为元胞属性，其结构简化图如附录B 图B3 所示。然后，根据附录B 表B2 所示的交通参数，结合1.2.1 节所建的交通流量预测模型获得各个路段（元胞）中交通流量的动态变化信息。最后，利用适合中国交通路况的回归路阻函数模型以及Floyd 算法进行MESS 的路径规划。其中，针对回归路阻函数模型中的回归参数k1和k2，可利用文献［19］提出的最大似然估计法进行计算。结合已知的交通参数，求解得到3 类路段的k1和k2分别为0.252 和0.748、0.288 和0.712 以及0.315 和0.685。

根据所提的两阶段优化框架，文中算例将3 h 作为一次长时间尺度优化的长度，将1 h 作为一次短时间尺度优化的长度。

3.2 孤岛运行结果分析

利用所提的配电网灾后孤岛运行策略对算例进行分析，得到的MESS 调度信息如表1 所示。MESS 的能量调度情况和孤岛拓扑变化信息分别如附录B 图B4 和图B5 所示。配电网一、二级负荷的灾后恢复结果如图4 所示。由于三级负荷恢复效果较差且恢复效益较低，为清晰展示其恢复率的动态变化过程，三级负荷的恢复率如附录B 图B6所示。

表1 MESS 调度信息Table 1 Scheduling information of MESS

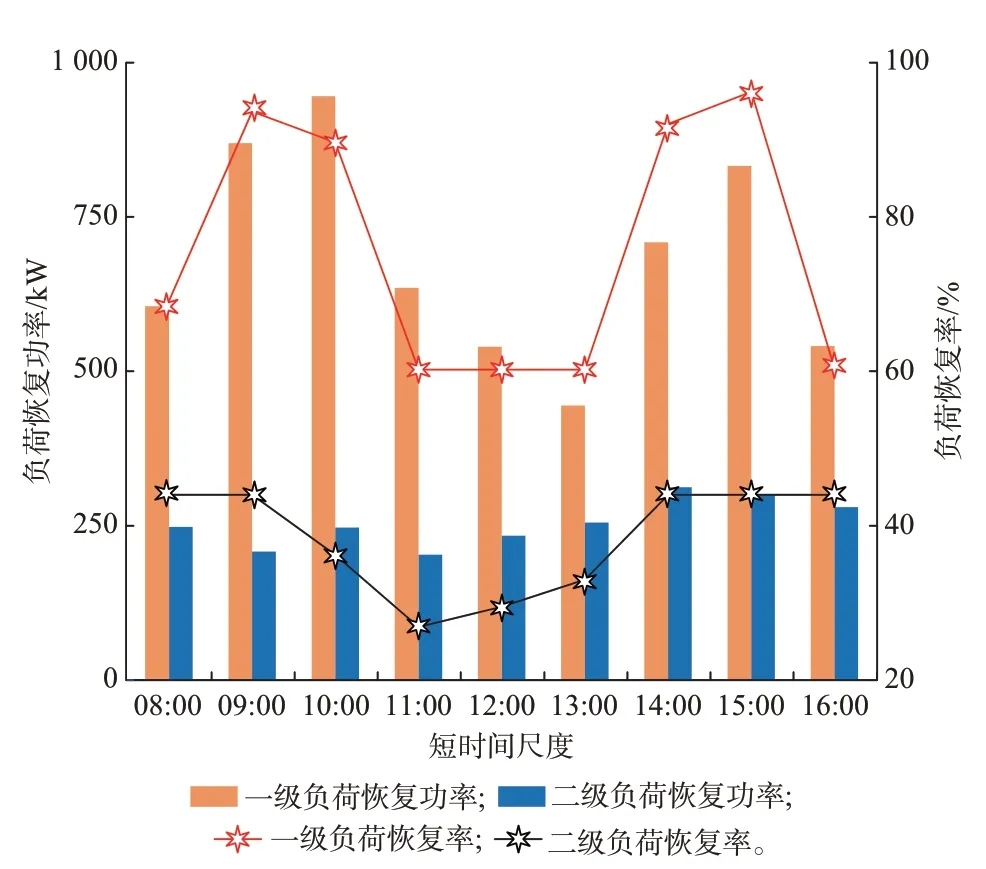
图4 灾后配电网负荷恢复结果Fig.4 Load restoration results of post-disaster distribution network

由图4 可知，所提的配电网灾后孤岛运行策略会使一级、二级负荷的恢复功率和恢复率呈现出不同程度的波动，这种现象是由负荷需求的时序波动性、孤岛拓扑信息的动态变化以及MESS 的调度情况共同决定的。

在08：00—09：00 时段，一级负荷恢复率显著低于09：00—11：00 时段的恢复率，而二级负荷恢复率变化不大。这是因为一级负荷优先级较高，MESS调度至供电区域后，主要为一级负荷供电，而二级负荷的恢复主要来自含DG 的孤岛区域。因此，二级负荷的恢复率不受MESS 供电区域恢复进度的影响。一级负荷在08：00—09：00 时段的恢复率低于09：00—11：00 时段的恢复率，这是因为MESS1 至少需要花费28 min 才能到达节点23，而MESS2 至少需要花费42 min 才能到达节点28，滞后了一级负荷的恢复进度。此外，10：00—11：00 时段的一级、二级负荷的恢复功率均有所提高但恢复率均有所下降，这是由该时段内一级、二级负荷的恢复需求量增加所造成的。

在11：00—14：00 时段，一级、二级负荷的恢复率相较于08：00—11：00 时段均有所下降。这是因为在11：00 后，MESS1 的能量不足以支撑下一个长时间尺度中的一级负荷恢复。因此，经过第2 个长时间尺度优化后，MESS1 被调度至节点5 处进行充电，行驶耗时36 min，节点24 处需求较大的一级负荷无法恢复，一级负荷恢复率降低。结合附录B 图B5 可知，在11：00—14：00 时段，DG1 与DG2 共同形成了一个多源孤岛，实现了所在区域的负荷恢复效果最大化，而MESS1 被调度至属于DG3 孤岛的节点5 处进行充电，DG3 在确保所属孤岛内的一级负荷完全恢复的同时，将剩余发电量转移至MESS1。因此，二级负荷恢复率也存在一定程度的下降。

在14：00—17：00 时段，相较于11：00—14：00 时段，一级负荷的恢复率先上升再下降，二级负荷的恢复率先上升再维持稳定。这是因为在该长时间尺度中，DG1 与DG3 形成了一个多源孤岛，DG3 所属孤岛区域的部分二级负荷重新得到了电力支撑；MESS1 从节点5 处离开，并耗时25 min 前往节点24处进行放电支撑，MESS2 依然停留在节点28 处进行放电。因此，一级、二级负荷的恢复率先得到了提升。考虑到二级负荷的恢复主要还是来自含DG 的孤岛区域，故二级负荷恢复率在后续时段维持稳定。而一级负荷恢复率在16：00—17：00 时段存在较大程度的下降，这是因为MESS1 在这一时段由于剩余容量的限制，无法完全满足一级负荷节点24的恢复需求。因此，一级负荷恢复率再次下降。

此外，MESS1 在11：00—14：00 时段从节点5 处获得的电量在14：00—17：00 时段自节点24 处进行了释放，这也说明了所提策略的另一优势：MESS 与DG 可以实现时-空双维度的协同，即以优先恢复重要负荷为目标，将原本分配给低优先级负荷的电量转移至MESS，而在其他时段再将该部分电量转移至其他区域的一级负荷，提高了社会总恢复效益，实现了电能的最优时空分配。

3.3 优化对比分析

3.3.1 孤岛运行策略对比

为了验证所提动态孤岛运行策略的优势，设置以下不同的对比策略进行分析：

对比策略1：不考虑DG 的多源协同能力，即利用单个DG 形成单个孤岛的传统方法进行独立孤岛运行，其余设置与所提策略一致。

对比策略2：考虑电源的多源协同能力，同时考虑交通路网下的MESS 调度，但仅进行一次最佳接入点的寻优，即仅进行单次调度，其余设置与所提策略一致。

对比策略3：考虑电源的多源协同能力，同时考虑交通路网下的MESS 调度，但不考虑交通流量的影响，仅利用基于最短路径长度的传统调度方法，其余设置与所提策略一致。

将所提策略与各策略进行对比，以验证所提策略的优势。经求解，所提策略、对比策略1、对比策略2及对比策略3 的加权负荷恢复量分别为32 874.41、31 671.39、30 666.42、32 564.83 kW。由此可看出，各对比策略的优化结果均与所提策略存在差异。根据文献［29-30］的配电网弹性分析可知，灾后配电网弹性水平的高低与加权负荷恢复量成正相关。因此，所提策略的配电网具有更高的弹性。

1）对比策略1

对比策略1 因没有考虑DG 的多源协同，DG1、DG2 和DG3 各自形成独立孤岛，有限的DG 功率无法得到最优分配，导致DG1 所在的孤岛区域中一级负荷恢复率降低，加权负荷恢复量相比于所提策略降低了1 203.02 kW。其中，对比策略1 的孤岛划分结果见附录B 图B7，一级、二级负荷的恢复率见附录B 图B8（a）。结果表明，对比策略1 虽然是属于可改变孤岛边界的动态孤岛划分方法，但并未考虑孤岛融合，阻断了电源间的联动能力。因此，计及多源孤岛融合手段的多源协同孤岛运行策略可以提高多电源在空间上的协调互补能力，充分发挥多源协同的优势，从而实现负荷恢复效果的进一步提高。

2）对比策略2

对比策略2 虽然考虑了多源协同，但并未充分发挥MESS 的时空灵活性，在仅进行单次调度的情况下，无法进一步发挥MESS 的能量时空转移能力，即无法将电量从DG 孤岛区域的低等级负荷转移至MESS 供电区域的重要负荷，仅能将自身容量的电量进行时间维度上的最优分配，无法进一步提高电能在空间维度上的分配能力。因此，相较于所提策略，加权负荷恢复量有较大减少。其中，对比策略2 的一级、二级负荷恢复率见附录B 图B8（b）。结果表明，基于能量时空转移的MESS 动态调度比仅进行一次MESS 调度更具优势，这是因为MESS 在配电网故障维修结束前就可能会出现电量提前耗尽的现象，如果只进行一次调度，MESS 则无法将其他区域内电源分配给低优先级负荷的多余电量转移至MESS 供电区域内的高优先级负荷，MESS 与其他电源间的协同能力受到限制，从而降低了总恢复价值。

3）对比策略3

在对比策略3 中，由于未考虑交通流量对MESS 路径规划的影响，加权负荷恢复量相较于所提策略也有一定程度的降低。这是因为在实际交通路网中，机动车与非机动车流量的动态变化会对实际调度时间产生影响，而基于最短路径长度得到的调度路径不一定是所需行驶时间最短的路径。在对比策略3 与所提策略中，MESS2 的调度路径相同，故负荷恢复效果的不同主要受MESS1 的影响。以11：00—14：00 时段为例，两策略的MESS1 调度路径结果对比如表2 所示。

表2 MESS1 调度路径对比Table 2 Scheduling path comparison of MESS1

可以看出，虽然对比策略3 的调度路径长度更短，但实际行驶时间比所提策略增加了11 min，这是因为交通节点24 与2、节点2 与3 之间的元胞流量更大，导致行驶时间增加，而所提策略在每次决策中都会通过流量预测模型得到流量最小的路径，规避了流量较大路段对调度过程的影响。同时，结合表1可知，11：00—14：00 时段属于MESS1 的充电时段，且MESS1 的总放电量大于其自身容量，而多出其自身容量的电量来自这一时段的充电量。这也表明所提策略可以使MESS1 更早地接入DG3 所属孤岛区域内的节点进行充电，从而将更多的电量由DG3所属孤岛区域的低优先级负荷转移至MESS 供电区域的一级负荷，通过缩短调度时间来改变电能分配结果，提高了总恢复价值。

此外，根据求解结果，所提策略中交通流量预测模型的求解耗时为6.04 s，远小于所节省的MESS调度时间，满足在线应用的需求。因此，考虑交通流量的影响具有更好的现实意义。

3.3.2 优化方法对比

为验证基于两阶段优化框架的优化方法的有效性，文中将单阶段优化方法（即不再进行长时间尺度优化，仅进行以1 h 为长度的短时间尺度优化）与其进行对比，对比结果如表3 所示。

表3 优化方法对比Table 3 Comparison of optimization methods

根据表3 所示的对比结果可以发现，两阶段优化的决策耗时仅为单阶段优化的23.6%，并且加权负荷恢复量仅降低了2.41%。这是因为在单阶段优化中，每个时段都需要对拓扑变量和MESS 接入点变量等大量整数变量进行重新决策，增加了决策难度和决策耗时，但目标函数的最优性得到了稍许提升；而在两阶段优化中，通过长时间尺度优化得到了拓扑变量与MESS 接入点变量的边界条件，决策难度和决策耗时显著减少，同时，用短时间尺度来优化在已知边界条件下的负荷恢复策略，使计算结果不会过多地偏离最优值。另外，由于两阶段优化中MESS 接入点的决策次数减少，流量预测模型的重新求解次数也随之减少，总决策时间进一步缩短，最终实现了决策耗时与计算精度的权衡。为进一步说明所提方法的扩展性和适用性，将在文中算例的基础上增加MESS 数量，由此得到的加权负荷恢复量与决策耗时结果如附录B 表B3 所示。由表B3 可知，随着MESS 数量的增加，所采用的两阶段优化方法依旧能在可预见的时间内完成求解，仍满足在线应用的需求。

此外，根据表3 可知，本文算例在单阶段优化中的孤岛拓扑变化次数比两阶段优化多了5 次，即单阶段优化中有8 个时段需要改变多个线路开关的开合状态，且MESS 总调度次数也比两阶段优化多了4 次，调度更为频繁，这均不利于决策者统筹规划配电重构系统与MESS 调度部门的协同配合。综上所述，所提策略更适合在两阶段优化框架的基础上应用于配电网灾后恢复。