基于多特征符号聚合近似和层次聚类的户变关系识别方法

周 赣，茅 欢，冯燕钧，华济民，曾 瑛

（1.东南大学电气工程学院，江苏省 南京市 210096；2.国网江苏省电力有限公司无锡供电分公司，江苏省 无锡市 214000；3.广东电网有限责任公司，广东省 广州市 510600）

0 引言

低压台区线损因在电网总损耗中占比较高而成为电力企业降损工作的重点［1］。正确的户变关系一方面可以保证线损统计的准确性和可参考性，另一方面为线损异常诊断工作的开展奠定基础，对线损治理具有重要意义。传统方法大多依靠人工核查来获取用户与台变的从属关系，效率低下，且拓扑日渐复杂，人工核查难以为继。近年来，随着智能电表（smart meter，SM）的普及和高级量测体系（advanced metering infrastructure，AMI）的不断完善，量测数据为台区线损的精益化管理提供了全方位的支撑［2］，依托这些数据进行户变关系识别，进而探寻更为准确的线损计算方法，已经成为理论研究和实际应用中的趋势。

目前，用户与台变之间的电压相关性分析是户变关系识别的重要依据，一些研究通过皮尔逊相关系数法［3-5］、灰色关联度分析法［6-7］等方法对用户与台变的从属关系进行梳理，但其准确性受限于数据预处理方式及人为设置的用以衡量电压相似度高低的阈值。由于户变关系识别实质上是要解决分类问题，另一些研究将聚类算法引入其中，相比于直接进行电压相关性分析，聚类算法具有更强的泛化能力，且能更有效地提取系统特征从而完成分类任务。文献［8］基于独立成分分析（independent component analysis，ICA）技术，以静态数据表征台区用户电压时序特征，随后利用k-means 聚类得到正确的户变关系。文献［9］利用变压器数目和各相出口电压已知的天然优势选取k-means 算法的聚类个数以及聚类中心，同时引入相关系数重新定义相似度的评估标准，从而提高识别准确率。文献［10］首先通过分段聚合近似（piecewise aggregate approximation，PAA）方法将电压曲线分段并降维，随后在引入一阶导数与动态时间规整（dynamic time warping，DTW）的基础上对k-means 算法加以改进，构建低压台区相位辨识模型。文献［11］通过t分布的随机近 邻 嵌 入（t-distributed stochastic neighbor embedding，t-SNE）方法实现台区用户电压数据降维，然后基于层次结构的平衡迭代归约和聚类（balanced iterative reducing and clustering using hierarchies，BIRCH）对用户相位及接入表箱进行辨识。文献［12］基于加速动态时间规整（fast dynamic time warping，Fast DTW）算法进行配变低压侧与用户侧电压曲线的相似性分析，然后采用基于融合自组织特征映射(self-organizing feature mapping,SOM）神经网络和k-means 的两阶段聚类算法进一步提升算法性能及计算效率。以上方法均在聚类前对数据进行降维处理，在保留了电压曲线主要特征的前提下，避免了长时间尺度数据带来的计算复杂、耗时严重的问题，提升了户变关系识别的效率。然而，当采集到的电压序列存在一定程度的数据缺失时，以上方法均需增设数据预处理环节，降低了求解效率，且最终户变关系识别的准确性极大地依赖于预处理效果的好坏，存在一定的局限。因此，寻求一种更为简单高效的电压曲线相似性特征提取方法，成为提升台区户变关系识别模型性能的关键。

本文提出了一种基于多特征符号聚合近似（multi-feature symbolic aggregate approximation，MF-SAX）和层次聚类的户变关系识别方法。首先，对传统的时间序列符号聚合近似（symbolic aggregate approximation，SAX）方法加以改进，不仅以符号化表达的方法来提升计算效率，还引入电压波动系数及变化趋势以便更好地提取电压曲线的动态特征；然后，采用编辑距离度量表征不同用户电压曲线字符串间的相似度，并结合层次聚类算法分析实际的户变关系，筛选出异常用户。实际算例结果表明，本文所提户变关系识别方法相比于现有方法准确率更高，误报更少，且当电压数据存在一定程度的缺失时无须增设插值预处理环节，具有更高的求解效率。

1 问题分析

错误的户变关系主要发生在同一供电片区或者相邻的供电片区，即给某个小区、街道或农村供电的几个邻近变压器及终端用户。本文对这一问题展开研究，在台区数目已知的片区内对用户和变压器的从属关系进行梳理。

配电网中的节点电压曲线主要有以下特性［13］：网络中同一个分支或者同一个配电变压器下的负载一般具有相似的电压曲线；负载之间的电气距离越近，其电压曲线的相似性越高。现分别从两个实际台区中随机抽取5 个用户的96 点日电压曲线，对上述相似度特性进行验证，采用式（1）计算电压序列X={X1，X2，…，Xs，…，Xn} 与Y={Y1，Y2，…，Ys，…，Yn} 之间的皮尔逊相关系数（Pearson correlation coefficient，PCC）C：

式中：n为电压序列的长度；Xs、Ys分别为序列X、Y中第s个电压的数值分别为序列X、Y的均值。

相关性热力图如图1 所示。图中：用户1 至5 来自台区1，用户6 至10 来自台区2。

图1 两台区用户电压曲线的相关性分析Fig.1 Correlation analysis of user voltage curves for two station areas

同一台区中用户的电气距离相对更近，其电压序列的相关性也会相应更高，而不同台区用户电压的PCC 值则会低于同一台区用户电压的PCC 值，反映在图1 中明显的色块差异上。由此可见，根据用户电压曲线的相似度差异进行台区户变关系识别具有一定的可行性。然而，当测试样本中的用户用电行为相似、电压波形接近时，仅以相似度差异作为判据显然是不可取的，需要探寻一种更为有效的户变关系识别方法。

2 基于MF-SAX 和层次聚类的户变关系识别方法

2.1 基于MF-SAX 的用户电压曲线表征方法

2.1.1 时间序列符号聚合近似方法

近年来，时间序列分析颇受欢迎，在实际应用中为了实现海量数据的快速分析，往往需要对长时间尺度下的数据进行降维处理。Keogh 等人提出了PAA 方法，将原始序列分割为若干条子序列，并利用分段均值表征各子序列的数值状况，相比于不做降维处理，在索引能力和计算速度上都取得了较大提升［14］。基于此，Lin 等人提出了SAX 方法，将分段均值映射到等概率区间，实现了高维连续数值到低维离散字符的转换，符号化表达在兼顾时间效率的同时大大提升了空间效率，在聚类、异常检测、可视化等数据挖掘任务中也表现出了更为优异的性能［15］。然而，降维处理难免会导致局部细节的丢失，可以引入附加参数，对时间序列的特征信息加以补充。常见的特征参数包括波动系数、变化趋势、峰度、偏度、自相关系数、峰峰值等，本文依托大量实验来评估这些特征参数对SAX 方法性能的提升效果。实验结果表明，相比于引入其他特征参数，引入波动系数和变化趋势其中之一便能够很好地区分不同用户的电压曲线，从而提升户变关系识别的准确率；而相比于引入单一特征参数，同时引入这两个特征参数能够从数据分布和动态变化两个不同的角度对电压曲线进行刻画，使算法能够出色地应对含有相似电压曲线的复杂情况。因此，本文将电压波动系数和电压变化趋势这两个附加参数引入传统SAX 方法中，提出了MF-SAX 方法，进一步加强了用户电压曲线的特征表达，为后续的户变关系识别模型提供了更为显著的特征输入。

2.1.2 附加参数的引入

1）电压波动系数

标准差反映了一组数据的离散程度，将电压检测值的标准差作为评价指标能够有效量化一段时间内配电网节点电压的波动情况［16］。各分段内的电压标准差可由式（2）计算得到：

式中：S为分段电压波动系数；d为该分段内的电压观测总数；Ug为该分段内的第g个电压观测值为分段电压均值。

2）电压变化趋势

曼肯德尔（Mann-Kendall，MK）法是一种对样本数据分布无特定要求的非参数检验方法，既能有效分析时序数据的变化趋势，又能克服序列中存在的少量异常或缺失值干扰。基于MK 趋势校验实现分段序列中电压动态变化趋势的符号化表达的步骤如下［17］。

步骤1：假设条件H0表示时间序列中样本点独立同分布，无相应的变化趋势。对于长度为m的用户电压子序列x={x1，x2，…，xp，…，xq，…，xm}，由式（3）计算检验统计量R。

式中：xp和xq分别为序列x中第p个和第q个元素的值；sgn(⋅)为符号函数。

步骤2：对于含有大量数据的样本，R服从正态分布，通过式（5）计算方差V（R）［18］。

步骤3：检验统计量Z满足式（6）。

在显著性水平α下进行双边趋势检验，当标准正态分布曲线左端与横轴所围面积为τ=1-α/2时，将对应位置处的横坐标记为Zτ。对于计算得出的检验统计量Z，若|Z|≥|Zτ|，则认为原假设H0不可接受，电压序列分段存在显著的变化趋势，Z>0时呈上升趋势，Z<0 时呈下降趋势；若|Z|<|Zτ|，则认为原假设H0是可接受的，电压序列分段呈平稳趋势［19］。本文给定显著性水平α=0.05，上升、平稳、下降趋势分别用符号I、S、D 表示。

2.1.3 基于MF-SAX 的电压曲线特征提取

1）大规模的样本数据集通常服从正态分布［20］，因而在较长时间尺度下提取长度为z的电压序列u={u1，u2，…，uh，…，uz}，并对其进行Z-Score 标准化处理，便能得到服从标准正态分布的新序列u′={u′1，u′2，…，u′h，…，u′z}，如式（7）所示：

式中：uh为原始电压序列中的第h个值；u′h为新电压序列中的第h个值；为原始电压序列的均值；σ为原始电压序列的标准差。

2）使用PAA 方法对u′进行处理，得到k个分段区间及第t个分段对应的电压均值Pt，1（t=1，2，…，k），计算各个分段内的电压波动系数Pt，2以及电压变化趋势Pt，3。对于电压曲线存在的少量缺失值，本方法直接以“-”表示，定义电压数据压缩率为z/k。

3）将电压均值及波动系数由数值映射为符号。在标准正态分布曲线上设置A-1 个断点，使之满足相邻两个断点所对应的概率值的相对间隔为1/A。在坐标平面上A-1 个断点的高度处进行水平切割，划分出A个等概率区间，分别对应于a、b、c等符号。当A的取值从3 变化到6 时，相应的断点序列B={B1，B2，…，BA-1} 如表1 所示。表中：BA-1为第A-1 个断点值。

表1 不同符号集的断点划分情况Table 1 Breakpoint division for different symbol sets

得到断点序列后，便可实现电压均值及波动系数的符号化转换：将所有小于B1的数值映射为符号a，将所有大于等于B1且小于B2的数值映射为符号b，依此类推。

4）符号融合，以字符串表征电压序列，u′最终转化为{P1，1，P1，2，P1，3，P2，1，P2，2，P2，3，…，Pk，1，Pk，2，Pk，3}。当符号数目取为5 且分段数目设置为6 时，某用户的日96 点电压曲线及其符号化表达生成过程如附录A 图A1 所示。

2.2 基于编辑距离的电压曲线相似性矩阵生成

经MF-SAX 处理后，各待检测用户的电压曲线从连续数值转换为离散字符串，相应地便能以文本处理或数据结构应用等多元化的形式进行后续的数据处理。本文采用编辑距离［21］（edit distance，ED）度量表征各用户电压曲线的字符串间相似度，其生成原理简单、可解释性强，因而逐渐成为自然语言处理领域中最为经典的文本匹配方法之一。两个连续非空字符串F与G之间的编辑距离可由下式计算得到：

式中：EF，G(i，j)为字符串F中的前i个字符与字符串G中的前j个字符之间的编辑距离；Fi为字符串F中的第i个字符；Gj为字符串G中的第j个字符；e为EF，G(i-1，j)、EF，G(i，j-1)、EF，G(i-1，j-1)三者中的最小值，分别对应于删除Fi、插入Gj以及将Fi替换为Gj这三种操作［22］。

以某两个实际用户对应的字符串片段为例，编辑距离矩阵的生成过程如附录A 图A2 所示。

2.3 户变关系识别流程

针对上述基于编辑距离生成的用户电压曲线相似性矩阵，采用层次聚类（hierarchical clustering，HC）算法进一步实现户变关系的识别。层次聚类是一种基于指定相似性度量准则构建嵌套聚类树的无监督学习方法，通过树状图对聚类结果进行可视化展示，由于操作灵活并且可以直观地展现类间层次关系而受到语义图像处理［23-24］等诸多研究领域学者的关注。考虑到相邻台区之间更容易产生户变关系错误匹配的问题［6］，所以首先根据地理信息系统（GIS）记录将距离相近的台区进行“捆绑”生成相邻台区集，再在该集合下开展户变关系梳理工作。图2 描述了基于MF-SAX 和层次聚类的户变关系识别算法流程。

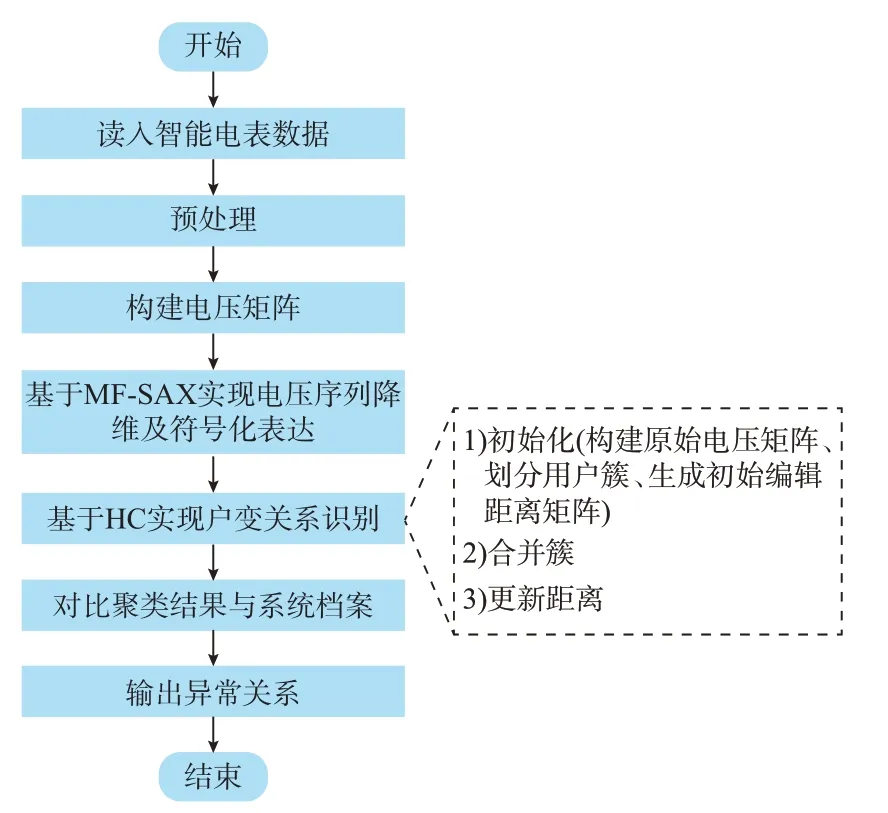
图2 户变关系识别流程图Fig.2 Flow chart of user-transformer relationship identification

1）用户电压矩阵构建：获取同一相邻台区集合下各用户的96 点电压数据，建立包含所有待检测用户的电压矩阵U0，如式（9）所示。

式中：Ua，b，c为用户c在第a天的第b个采样点处的电压值；M为待检测台区的用户总数；N为采样的时间跨度。

2）距离矩阵初始化：将每个用户划分为一个单独的簇，并以T1表示第1 个用户簇，以T2表示第2 个用户簇，依此类推，得到待检测用户初始簇集合T0={T1，T2，…，TM}，随后令用户簇集合T=T0，基于编辑距离的计算方法，获取电压曲线初始距离矩阵DM。

式中：Ev，w为用户v和用户w电压字符串之间的编辑距离。

3）用户簇合并：将用户簇集合T中距离最近的两个簇Tv和Tw合并为一个新簇Tvw，得到新的用户簇集合，即此时T从{T1，T2，…，Tv，…，Tw，…，TM}变为{T1，T2，…，TM，Tvw}。

4）距离更新：计算Tvw和T中其他用户簇之间的距离，并更新距离矩阵。

5）重复步骤3）和步骤4），当所有用户聚为一类时，停止循环。

6）在包含距离信息的树状图中进行水平切割，使上半平面的分支数等于所需的类别数量，从而得到聚类结果。

7）将HC 模块生成的聚类结果与原始系统拓扑档案进行对比，筛选出户变关系异常的用户。

3 MF-SAX 方法的有效性分析

从江苏省南京市某小区下的两个相邻台区中截取17 个表箱对应的同相电压曲线片段，构建测试样本，对SAX 不压缩、SAX 压缩、MF-SAX 相同压缩率三种方法进行错误识别数量和计算时间的对比分析。

实验在Windows 10 操作系统的Pycharm（基于Python 3.7）环境下进行，硬件配置为1.80 GHz Intel Core i5-5350U CPU。17 个表箱的电压曲线片段如图3 所示。图中：1 至14 号表箱隶属于台区1，记为正常用户，15 至17 号表箱隶属于台区2，记为异常用户。

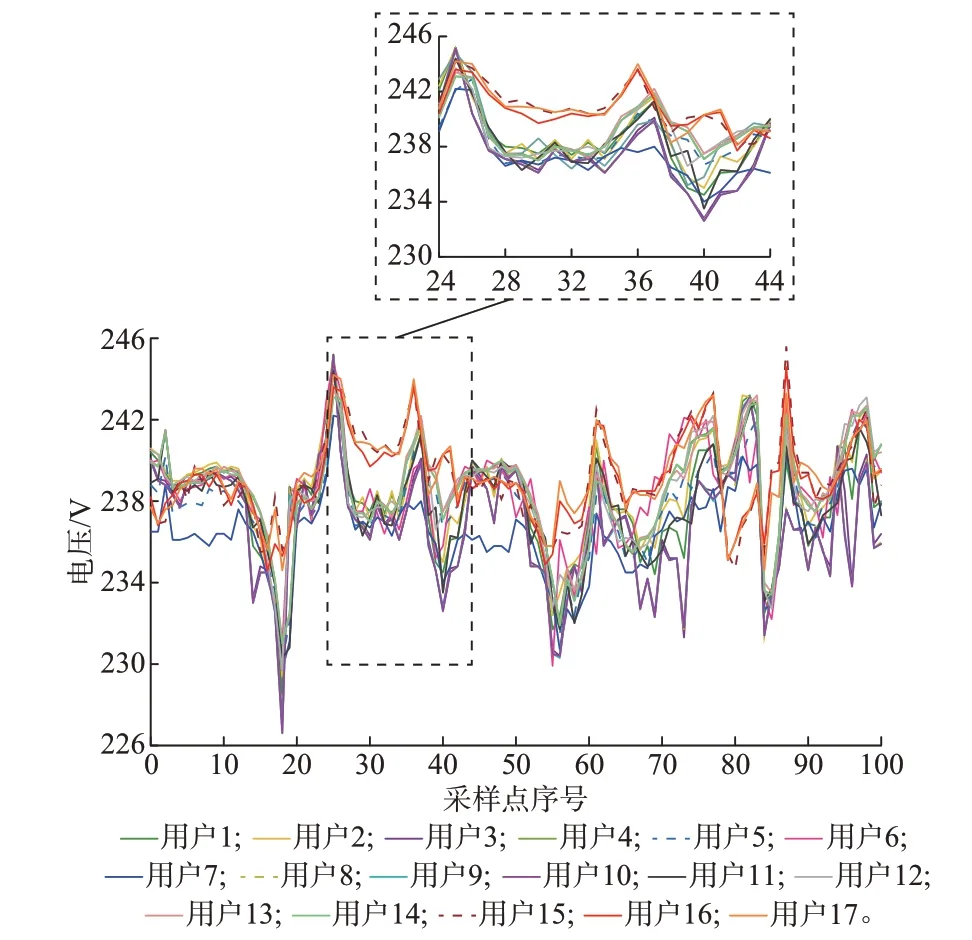
图3 电压曲线示意图Fig.3 Schematic diagram of voltage curves

在实验过程中将符号数目设置为5，将压缩率设置为20。SAX 不压缩、SAX 压缩与MF-SAX 相同压缩率三种方法生成的用户电压编辑距离矩阵热力图如图4 所示。图中：色块颜色越深，表示用户电压曲线的相似度越低。

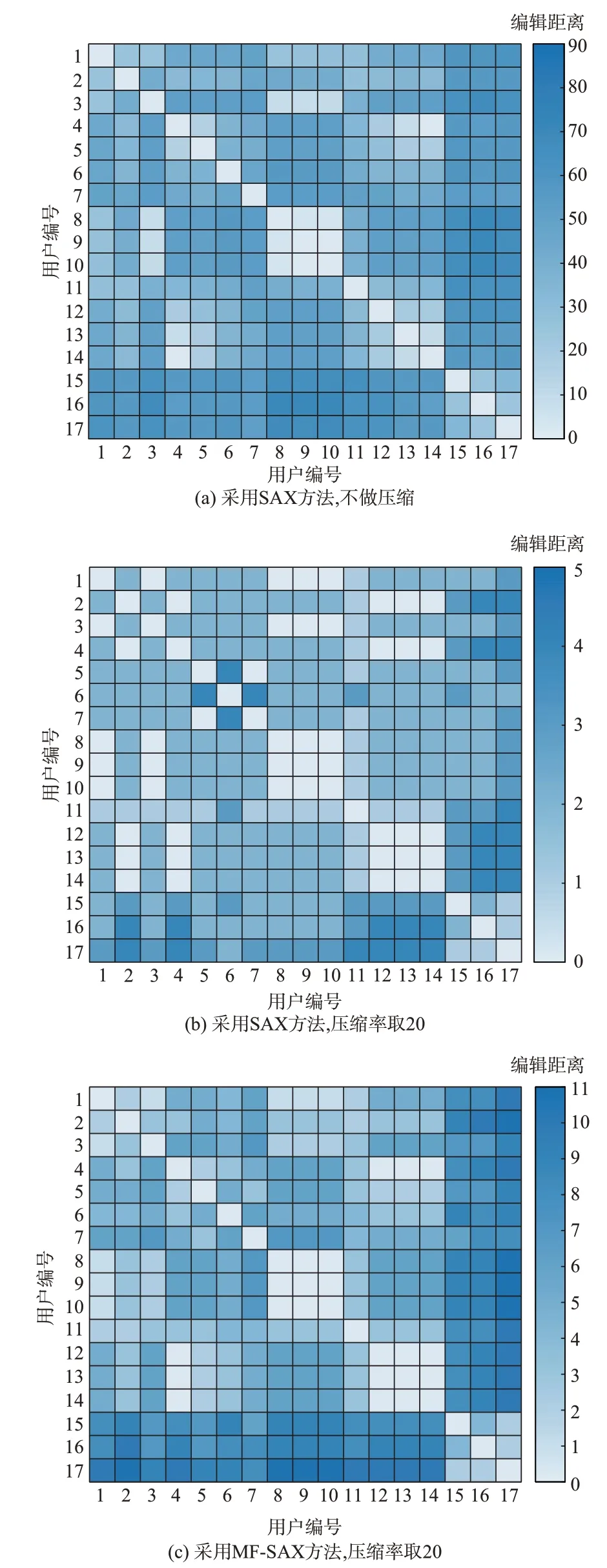
图4 三种方法生成的用户电压距离矩阵对比Fig.4 Comparison of user voltage distance matrices generated by three methods

分析图4 可知，SAX 压缩方法生成的热力图并不符合台区内部颜色浅、台区之间颜色深的规律。SAX 不压缩方法生成的热力图虽然基本符合这一规律，但是台区内外的颜色深浅对比不够强烈。相比之下，本文提出的MF-SAX 方法能够有区分度地体现不同台区之间用户电压曲线的差异，热力图中第15 至17 行和列的颜色明显深于左上角和右下角的正方形区域，表明正常用户和异常用户已经能够被区分开来。

表2 给出了三种方法的错误识别数量和计算时间。使用传统SAX 方法时，无论是否进行压缩处理，都发生了误报（将户变关系正常的用户识别为异常），说明当相邻台区之间的用户电压曲线较为相似时，仅仅依靠分段内的电压均值并不能有效地区分隶属于这些台区的用户。而MF-SAX 方法引入了电压波动系数和电压变化趋势这两个附加参数，使每一个分段内提取到的电压特征得到补充，更为全面地凸显了用户电压曲线之间的动态差异，提升了户变关系识别的效果。表2 结果表明，MF-SAX 方法既能将台区2 中混入的3 个异常用户全部筛选出来，又不存在误报的情况，户变关系识别结果完全正确，可见其实用性和有效性。

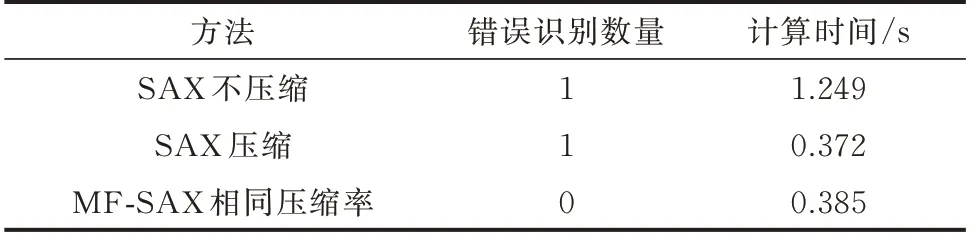
表2 三种方法的识别效果对比Table 2 Comparison of identification effect of three methods

此外，MF-SAX 方法的另一优势在于通过压缩处理来减少计算时间。分析表2 可知，当压缩率相同时，MF-SAX 方法与SAX 方法的计算时间非常接近，均明显少于SAX 不压缩方法，说明压缩处理能够加快方法的求解速度，提升求解效率。

4 算例分析

4.1 算例介绍

选择江苏省南京市某个具有正确拓扑档案的小区，对MF-SAX+HC 模型在户变关系梳理场景中的效果进行验证。该小区已知共有4 个台区，经现场梳理及历史线损统计分析后确认分别包含37、83、97、65 个用户。以4 个台区的用户电压数据及变压器低压侧电压数据混合构建测试样本，完整数据集为台区历史数据中采集率为100%的96 点电压数据，时间长度为7 天。数据组成方式如表3 所示。

表3 测试算例的数据组成Table 3 Data composition of test example

4.2 评价指标

为了评估模型性能，采用准确率（accuracy）fACC、标准化互信息（normalized mutual information）fNMI［25］和FMI（Fowlkes-Mallows index）fFMI作为评价指标。

fACC反映了识别正确的用户数在总用户数中的占比，用于评价户变关系识别模型的整体准确程度。

式中：y为待检测的用户总数；为聚类结果中第r个用户的类别标签，一般用数字表示；Lr为第r个用户的实际类别标签；δ(·，·)为判别函数，当两个自变量相等时取值为1，否则取值为0；ρ()为置换映射函数，将由数字映射为与Lr同名的标签。

fNMI是一种衡量两个序列数据分布相关性的评价指标，反映了聚类质量的好坏。

式中：J为实际类别数目；K为聚类产生的类别数目；yλ为实际分类中第λ个类别所包含的用户数目；yμ为聚类结果中第μ个类别所包含的用户数目；yλ，μ为上述两个类别的交集所包含的用户数目。

通过对比用户聚类输出结果与台区营销档案，可将户变关系模型的识别结果分为真阳性（true positive，TP）、假阳性（false positive，FP）、真阴性（true negative，TN）、假阴性（false negative，FN）4 种情况，对应的样本数量分别记为WTP、WFP、WTN、WFN，则fFMI计算如下：

4.3 测试方法选择

选择SAX+HC 方法、Pearson 相关系数识别法［3］、PAA+DTW-AP［26-27］方法以及t-SNE+BIRCH［11］方法，与本文所提MF-SAX+HC 方法进行对比。在MF-SAX+HC 方法以及SAX+HC 方法中，将压缩率设置为22，将符号数目设置为5；Pearson 相关系数识别法设置相关性判别阈值为0.8；对于PAA+DTW-AP 方法，将压缩率同样设置为22；t-SNE+BIRCH 方法经过参数优化，最终将t-SNE 实现的空间维度设置为3。

4.4 模型性能对比

对于本文所提MF-SAX+HC 模型以及其余对比模型，分别考察其在完整数据集下的表现以及处理数据缺失问题的能力。完整数据集下各模型的性能对比结果如表4 所示。

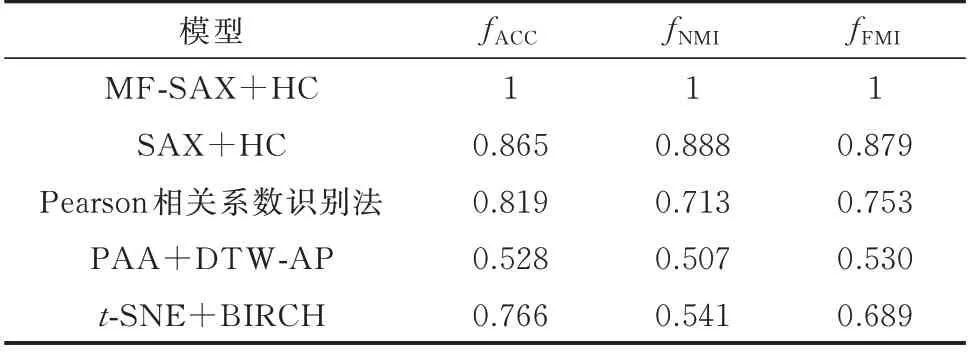
表4 完整数据集下各模型的性能对比Table 4 Performance comparison of models with complete data set

采用MF-SAX+HC 模型进行户变关系识别时，HC 模块生成的树状图见附录A 图A3，横坐标为用户/变压器编号，由于空间限制，不再进行展示。在自下而上的聚类过程中，用户根据距离远近逐层汇聚成簇。初始阶段各个用户自成一簇，随着簇与簇不断合并，最终所有用户聚为一簇。随后在树状图中进行水平切割，已知测试样本包含4 个台区，因而选择合适的切割高度，使其恰好被划分为4 类，切割分类过程以图A3 中的水平虚线表示。

随后模拟数据缺失的情况。以完整数据集为基础，随机选取其中2%的数据并将其置为空值，得到缺失率为2%的样本数据。考虑到除符号化表达方法外其余各方法均无法直接应对数据缺失问题，在使用前均先采用最近邻插值作为电压数据缺失值的填补。各模型的参数设置与处理完整数据集时保持一致，其性能对比结果如表5 所示。

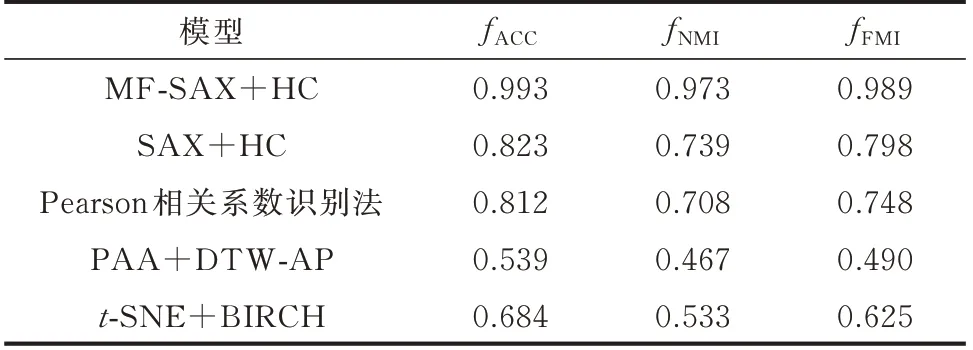
表5 数据缺失时各模型的性能对比Table 5 Performance comparison of models with data missing

综合分析户变关系识别结果与表中的性能指标，得到如下结论：1）相比于传统SAX 方法，MFSAX 方法通过引入电压波动系数和电压变化趋势这两个附加参数，强化了用户电压曲线的特征表达，综合利用了用户电压数据的静态数值特征和动态变化特征，提高了户变关系识别的准确率；2）在处理数据缺失问题时，符号化表达方法可以直接将样本数据代入求解，而其余各方法在使用前必须先进行插值预处理，导致工作量增加、求解效率降低；3）无论样本数据是完整还是缺失，MF-SAX+HC 模型的各项性能指标都明显优于其余对比模型，可见其不仅在完整数据集下具有出色的表现，在处理数据缺失问题时也能够很好地保证识别准确率。

5 结语

本文提出了一种基于MF-SAX 和层次聚类的户变关系识别方法。首先，阐述了基于用户电压曲线的户变关系识别原理；然后，通过引入电压波动系数和电压变化趋势两个附加参数来改进只以均值为变量的传统SAX 符号化表达方法；最后，提出了基于MF-SAX 和层次聚类的台区户变关系识别流程。算例结果表明，本文所提MF-SAX+HC 方法在充分挖掘了用户电压曲线蕴含的静态与动态特征信息之后，相比于现有方法准确率更高，误报更少，且在使用前无须预先进行用户电压数据的缺失值的填补，具有更高的求解效率。

然而，本文所提户变关系识别方法仍存在一定的局限性：一方面，研究过程中采用的数据主要来自信息采集成功率高且量测设备齐全的新台区，而缺乏对设备条件相对较差的老旧台区的研究；另一方面，压缩率的选取会对识别结果产生一定的影响，虽然可以依据经验来大致确定取值范围，但要获得最优解还需进行人工调节。未来，将针对以上两点对所提方法做出改进和完善。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。