融合信息物理社会因素的配电网可靠性评估方法

卢俞帆，刘 念，高舜安

（1.新能源电力系统国家重点实验室（华北电力大学），北京市 102206；2.国网冀北电力有限公司，北京市 100054）

0 引言

在重大社会活动背景下，电力企业需建立包括落实保障工作方案、重要基础设施的巡视检查等在内的重大活动电力安全保障工作机制，确保活动期间电力系统可靠运行［1］。配电网可靠性指标能够反映配电网按可接受质量标准和所需数量，不间断向系统末端用户供电的能力。通过可靠性评估，可以辨识配电网的薄弱环节，以便采取更有效的措施提升供电可靠性。近年来，随着新型电力通信、物联网、人工智能等技术的发展，配电网已成为融合信息物理社会因素的大规模复杂系统［2］，是能源领域信息物理社会系统（cyber-physical-social system，CPSS）［3］的重要组成部分。为准确量化信息、社会因素对配电网物理系统可靠性的影响，支撑面向重大社会活动的可靠性保障方案设计，亟须研究融合信息物理社会因素的配电网可靠性评估方法。

从信息系统的视角，一部分研究从信息系统功能特性的角度出发，考虑了信息系统功能失效［4-6］与信息传输可用性不足［7-11］对系统可靠性的消极影响。与上述研究不同，本文考虑了信息技术的应用对系统可靠性的积极影响。另一部分研究从信息系统技术应用的角度出发，运用在线监测数据，量化内部缺陷［12-16］与外部环境［17］因素对设备可靠性的影响，构建设备时变故障率模型。基于上述研究，本文综合考虑了信息系统缺陷识别、风险预警与社会系统缺陷消除、风险排查的共同作用，构成可靠性提升技术闭环。

从社会系统的视角，一部分研究从人因可靠性［18］的角度出发，量化了技术人员工作经验、心理状态等因素与缺陷消除率的关系［19-20］；另一部分研究从安全保障的角度出发，研究了如何制定科学的巡检、抢修方案。针对巡检工作，现有研究主要关注巡检周期对经济成本［21-25］与风险成本［24-28］的影响。针对抢修工作，主要研究集中于分析故障定位、复电操作时长对停电时间的影响［29-30］。

目前，有关配电网CPSS 的可靠性评估，存在以下问题：1）仅考虑了信息社会因素对物理系统可靠性的消极影响，忽略了信息技术作用与社会运维检修工作对可靠性的积极影响；2）分别研究了信息、社会各类因素对设备时变故障率、缺陷消除率的影响，未考虑信息社会因素协同作用对缺陷消除的综合影响；3）仅关注于人工巡检的作用，缺乏对巡检业务信息化现状的考虑；4）针对抢修工作的研究较为局限，忽略了故障定位技术、交通路况与保障物资对抢修工作的综合影响。

针对上述问题，本文提出了融合信息物理社会因素的配电网可靠性评估方法。首先，提出可靠性评估的信息物理社会交互框架。其次，在巡检业务信息化背景下，构建了设备发展型、破坏型故障状态转移模型，量化信息系统技术作用周期，社会系统人员缺陷消除水平、风险排除能力与设备故障率的关系。接着，构建故障恢复时间模型，全面量化故障定位技术精度，交通路况、保障物资充裕度与故障恢复时间的关系。最后，基于上述故障率与恢复时间，运用解析法计算系统可靠性，计算结果能够反映信息技术与社会保电工作的综合作用。

1 配电网可靠性评估的CPSS 交互框架

配电网CPSS 包含物理系统、信息系统以及社会系统3 个要素。其中，物理系统要素由电力线路、变压器、开关等物理设备构成；信息系统要素由设备状态感知系统、智慧运维保障系统、调度系统、地理信息系统和应急管理系统构成；社会系统要素则由运维、检修人员，应急车辆和物资构成。

配电网中物理设备故障按照形成机理可分为以下两类：1）发展型故障，设备从正常状态经过缺陷状态，最终发展为故障状态，此过程与设备自身老化情况密切相关；2）破坏型故障，设备受外部因素影响在短时间内由正常状态转变为潜在风险状态，最终发展为故障状态。破坏因素包括极端天气、人或动物的破坏行为等。

配电网CPSS 中，CPSS 间通过交互实现互相支撑、协同互补，提高配电网可靠性，各系统间相互作用关系如图1 所示。

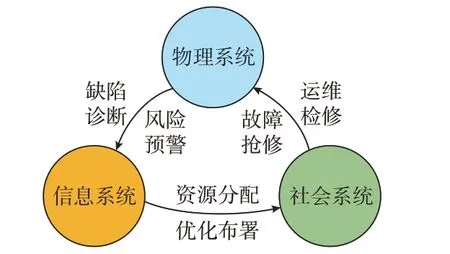
图1 配电网可靠性评估的CPSS 交互框架Fig.1 CPSS interaction framework for reliability assessment of distribution network

1）物理→信息：运用信息系统中的缺陷诊断、风险预警技术，识别设备早期缺陷并对设备所处环境中的破坏型风险因素提前预警。

2）信息→社会：通过信息系统对运维检修工作中所需的人、车、物等社会要素进行优化部署与调配，辅助完成日常运维检修与故障发生后的应急抢修工作。

3）社会→物理：通过社会系统运维检修工作对设备状态进行诊断、对风险因素进行排查，进一步降低设备故障概率；通过应急抢修工作完成对故障设备的修复，对失电负荷的复电。

2 CPSS 环境下的配电网设备可靠性模型

2.1 考虑信息社会因素的发展型故障状态转移模型

针对发展型故障，可将“正常-故障”两状态模型扩展为“正常-缺陷-故障”的三状态模型，定义了设备发展型故障状态转移模型，如图2 所示。在设备由正常状态发展为缺陷状态的过程中，信息系统缺陷诊断技术通过采集设备健康状况信息，及时发现设备内部缺陷［31］；进一步，通过社会系统运维检修人员的消缺工作使处于缺陷状态的设备恢复到正常状态。

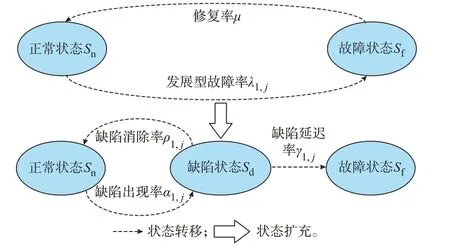
图2 配电网CPSS 中设备发展型故障状态转移Fig.2 Developmental fault state transition of equipment in CPSS of distribution network

发展型故障状态转移过程定义为发展型故障下设备状态和状态转移率的集合Pde={Sn，Sd，Sf，α1，j，ρ1，j，γ1，j，λ1，j，μ}，其中：Sn、Sd、Sf分别为设备正常状态、缺陷状态和故障状态；α1，j为缺陷出现率，表示单位时间内第j类设备缺陷出现的平均次数，由设备历史缺陷数据统计得到；ρ1，j为缺陷消除率，表示单位时间内发现第j类设备的缺陷并成功修复的次数，受设备健康指数和运维、检修人员缺陷修复效果的影响；γ1，j为缺陷延迟率，表示单位时间内缺陷设备发生故障的平均次数，由设备历史缺陷数据统计得到；λ1，j为发展型故障率，表示单位时间内第j类设备发生发展型故障的平均次数，受缺陷出现率、消除率和延迟率的影响；μ为修复率，表示单位时间内设备故障得以成功修复的平均次数，受社会系统人员、物资部署的影响。

2.1.1 缺陷出现率

设备在老化过程中经历缺陷状态，如不加干预则最终发展为严重故障造成停电［32］。设备由缺陷状态发展为严重故障的时序过程如图3 所示。图中：Tn、Tn+1、Tk、Tk+1分别为第n、n+1、k、k+1 个诊断周期对应的时刻。

图3 设备缺陷发展过程Fig.3 Developmental process of equipment’s defects

由于泊松分布适合于描述单位时间内随机事件发生，可假设在一定时间内电力设备出现缺陷的概率服从缺陷出现率为α1，j的泊松分布，如式（1）所示。

式中：P1，j（X=k）为第j类设备单位时间内出现k次缺陷的概率，其中，j∈NEq，NEq为设备种类集合。

2.1.2 缺陷消除率

在上述缺陷发展过程中，通过提前干预消除设备缺陷能有效降低设备故障率，用缺陷消除率ρ1，j来表征干预的效果。干预效果受到设备健康指数［33］和修复效果的共同影响，具体关系如式（2）所示：

式中：βj为第j类设备的消缺比，表示运维、检修人员修复设备缺陷的成功率；H为配电设备健康指数，可通过在线监测数据、检修报告和试验测试结果等方式获得；Kj和Cj均为第j类设备对应的模型适应性参数，且j∈NEq。不同类型设备对应不同的适应性参数，可基于中国某地区配电网2021 年设备运行工况统计数据通过拟合得到，各类设备的模型适应性参数如表1 所示，参数来源及拟合过程详见附录A。

表1 配电设备缺陷消除率计算参数Table 1 Calculation parameters for defect elimination rate of distribution equipment

由式（2）可知，设备缺陷消除率随健康指数增大而增大。进一步结合表1 中数据可知，电缆的缺陷消除率随健康指数的变化最为明显，说明设备健康状况对电缆缺陷发展过程的影响较为显著，可以通过提升电缆健康状况来抑制缺陷与故障的发生。

2.1.3 缺陷延迟率

设备发展型故障延迟时间h1，j为第j类设备由缺陷状态发展成故障状态的耗时。h1，j服从指数分布，其概率密度函数f(h1，j)和概率分布函数F(h1，j)分别如式（3）和式（4）所示。

式中：γ1，j为第j类设备的缺陷延迟率。

2.1.4 发展型故障率

基于上述故障延迟时间的概率密度函数，得到设备缺陷发展为故障的概率如式（5）所示：

式中：p1，j(t|m)为第j类设备在m时刻出现的缺陷在t时刻发生故障的概率；PD，j为第j类设备处于缺陷状态的概率；Td，n和Td，k分别为第n个和第k个等效诊断周期；Td为等效诊断周期，其与实际诊断周期T0，d之间的关系如式（6）所示；q为用于构造实际诊断周期与等效诊断周期关系的适应性参数，取值为正整数。

基于图2 所示的三状态转移模型，根据文献［34］中介绍的状态转移矩阵简化计算方法，得到设备处于缺陷状态的概率如式（7）所示，推导过程详见附录B。

由图3 可知，处于正常状态的设备在发展为缺陷状态后可进一步发展为故障状态或经过运维人员的修复后恢复正常。因此，从统计意义上说，单位时间内设备的缺陷出现次数等于发现缺陷并成功修复的次数与设备由缺陷发生故障的次数之和，即缺陷出现率等于缺陷消除率与延迟率之和，如式（8）所示。将式（8）代入式（7），化简得到式（9）。

进一步，计算截至t时刻第j类设备的故障发生率pj(t)，如式（10）所示。

将式（4）代入式（10）可得：

2.2 考虑信息社会因素的破坏型故障状态转移模型

针对破坏型故障，可将“正常-故障”两状态模型扩展为“正常-风险-故障”的三状态模型，定义了设备风险状态转移模型，如图4 所示。其中，在设备由正常状态发展为风险状态的过程中，信息系统风险预警技术通过捕捉风险强度信息，及时发现设备外部风险［35］；进一步通过社会系统运维检修人员的风险排查工作，使处于风险状态的设备恢复到正常状态。

图4 配电网CPSS 中设备破坏型故障状态转化Fig.4 Destructive fault state transition of equipment in CPSS of distribution network

与发展型故障类似，破坏型故障状态转移过程定义为破坏型故障下设备状态和状态转移概率的集合Pbr={Sn，Sr，l，Sf，α2，l，j，ρ2，l，j，γ2，l，j，λ2，l，j，μ}，其中：Sr，l为设备第l种风险状态；α2，l，j为风险出现率，表示第j类设备在单位时间内第l种风险因素出现的平均次数，由设备历史风险数据统计得到；ρ2，l，j为风险抑制率，表示单位时间内发现第j类设备所处环境中第l种破坏型风险并成功抑制的次数，受风险强度和运维、检修人员排除风险能力的影响；γ2，l，j为风险延迟率，表示单位时间内处于第l种破坏型风险状态的第j类设备发生故障的平均次数，由设备历史风险故障数据统计得到；λ2，l，j为破坏型故障率，表示单位时间内第j类设备发生第l种破坏型风险所致故障的平均次数，受风险出现率、延迟率和抑制率的影响。

2.2.1 风险出现率

和缺陷类似，第l种风险出现的概率服从风险出现率为α2，l，j的泊松分布。同样，可假设在一定时间内电力设备出现第l种破坏型风险的概率服从风险出现率为α2，l，j的泊松分布，如式（14）所示。

式中：P2，l，j(X=k)为第j类设备单位时间内出现k次第l种破坏型风险的概率，其中，j∈NEq，l∈NR，NR为破坏型风险种类的集合。

2.2.2 风险抑制率

当设备所处环境中出现如雨雪冰冻、施工作业等潜在破坏因素后，配电网运行异常势态感知技术能够结合预知的异常事件，根据预先设定好的关键特征阈值，实现异常隐患挖掘及风险预警。运维检修人员根据预警数据采取相应措施来抑制破坏型故障风险。抑制效果由风险抑制率ρ2，l，j表征，风险抑制率和风险抑制指数的计算方法分别如式（15）和式（16）所示。

式中：Al，j为第j类设备的第l种破坏型风险抑制指数；RN，l，j为第j类设备的第l种破坏型风险的实时强度，其计算方法如式（17）和式（18）所示；Ql为运维检修人员针对第l种破坏型风险的排除率；κl，j为故障率计算参数。

式中：RHis，l，j为第j类设备的第l种破坏型风险的历史风险强度。本文中考虑了强风、雨雪冰冻、车辆破坏和施工作业在内的4 种可能导致正常设备即刻故障的破坏型因素；NHis，l，j为过去一年内第j类设备由第l种破坏型风险所引发的故障次数；SN，l，j为设备所处环境中第l种破坏型风险实时强度；SˉHis，l，j为第l种破坏型风险强度在过去一年内的平均统计值［35］。

根据中国某地区配电网2021 年设备运行工况统计数据，结合上述模型确定设备的各类风险对应的故障率计算参数如表2 所示，参数拟合过程详见附录A。

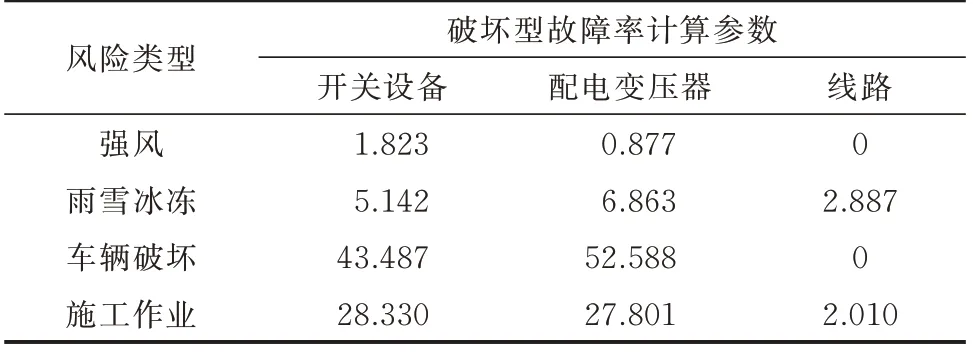
表2 配电设备各类破坏型故障率计算参数Table 2 Calculation parameters of various destructive fault rates of distribution equipment

2.2.3 风险延迟率

与设备发展型故障延迟时间h1相同，设备第l种破坏型故障延迟时间h2，l也服从指数分布，其概率密度函数和概率分布函数分别如式（19）和式（20）所示。

式中：γ2，l为设备第l种破坏型风险延迟率。

2.2.4 破坏型故障率

同样基于故障时间延迟模型，推导过程参考2.1.4 节，可得到设备各类破坏型故障率如式（21）所示。

式中：PR，l，j为第j类设备处于第l种破坏型风险状态的概率，推导过程详见附录B，与式（9）类似，PR，l，j的计算方法如式（22）所示；Tr，l为第l种破坏型风险的等效预警周期，其与实际风险预警周期Tr，0，l间的关系如式（23）所示。

式中：qr，l为用于构造第l种破坏型风险的等效预警周期与实际风险预警周期关系的适应性参数。

基于设备各类破坏型故障率计算得到设备总破坏型故障率，如式（24）所示。

2.3 考虑信息社会因素的设备故障恢复时间模型

设备的故障恢复时间包含故障定位时间、路程时间和维修时间3 个部分。故障定位时间受故障定位技术［36］精度与覆盖情况的影响；路程时间受保障点到故障点间的距离、交通路况以及抢修车辆的平均行驶速度的影响；维修时间受运维检修人员专业素质以及应急物资充裕度的影响，如式（25）所示。

式中：ui为设备i的故障恢复时间；d∈[0，1]为故障定位技术精度，d=0 表示设备所处位置无故障定位技术覆盖，d=1 表示故障定位精度达到100%，即设备i处发生的故障可由故障定位技术准确判断；uloca，i(⋅)为设备i的故障定位时间函数；Db，i为应急保障点b与设备i之间的地理距离；ωb，i为应急保障点b与设备i之间的路况因子；urou，b，i(⋅)为维修人员从保障点b到设备i间的路程时间函数；ure，i，c(⋅)为运维检修人员c修复设备i的平均维修时间函数；εb为保障点b的应急物资充裕度水平；i∈ΩE，b∈ΩDE，c∈ΩF，其中，ΩE、ΩDE和ΩF分别为设备、保障点和运维检修人员的集合。

故障定位时间由故障定位技术精度与覆盖情况共同决定，具体关系如式（26）所示。

式中：uloca，i，0为不考虑故障定位技术作用时设备i的原始故障定位时间，通常为3～8 h；r为模型修正系数。

运维检修人员从保障点b到设备i间路程时间的计算方法如式（27）所示。

式中：vtr为抢修车辆的平均行驶速度。路况因子ωb，i与车流密度fb，i相关［37］，具体关系如式（28）所示。

运维检修人员c修复设备i的平均维修时间［38］受应急物资充裕度影响，具体关系如式（29）所示。

式中：ure，i，c，0为运维检修人员c在εb为0 时的平均维修时间；l1为模型修正系数，此处可置为1。应急物资充裕度水平εb的取值可分别为0、1、2，受到物资数量指数、物资类型指数的综合影响，具体关系如式（30）所示。

式中：Mb为保障点b的物资数量指数；Cb为保障点b的物资类型指数，当物资数量、类型充足时Mb、Cb为1，否则为0。

综上所述，基于以上设备故障修复时间模型，得到综合考虑交通路况、运维检修人员专业素质和应急物资充裕度的恢复率如式（31）所示。

式中：μi为设备i的故障恢复率。

3 融合信息物理社会因素可靠性评估流程

融合信息物理社会因素的配电网可靠性评估流程如图5 所示。

图5 融合信息物理社会因素的配网可靠性评估流程Fig.5 Reliability evaluation process of distribution network incorporating cyber-physical-social factors

首先，对可靠性计算参数进行预处理。通过输入设备的各类风险强度、风险排除率计算风险抑制指数与各类风险抑制率，进一步结合设备的各类风险出现率与风险预警技术作用周期计算设备破坏型故障率。

其次，通过输入设备健康指数和运维、检修人员消缺比计算设备缺陷消除率。根据缺陷消除率计算缺陷延迟率，进一步结合缺陷延迟率与缺陷诊断技术作用周期计算设备发展型故障率。

然后，由车流密度计算保障点到故障设备的路况因子、物资数量和类型指数计算物资充裕度。结合保障点到故障设备间的距离和车辆行驶速度计算设备故障恢复时间。

最后，根据处理后的设备故障率、故障恢复时间，结合待评估区域配电网拓扑结构，运用解析法对配电网可靠性展开评估。运用解析法的过程中需要获得电源点到负荷点的最小路上的设备与线路，将非最小路上的设备与线路通过串并联等效折算到最小路上，最终形成各负荷点的故障率、停电时间列表并计算负荷点可靠性指标，基于负荷点可靠性指标进一步计算系统可靠性指标［34］，详细计算步骤见附录C。

4 算例分析

4.1 基础数据

本文的物理系统算例结构参考IEEE RBTS BUS 6［39］，系统拓扑与应急保障点保障范围如附录D 图D1 所示，各保障点到保障范围内各设备的距离、车流密度如表D1 至表D6 所示。根据中国某地区配电网2021 年设备可靠性指标与设备故障责任原因统计结果，可得物理系统中设备可靠性参数如表3 所示。针对2022 年某国际级重大赛事设置了不同等级的保电方案，各方案对应的可靠性模型参数如表4 所示。负荷点信息以及配电线路信息分别如附录E 表E1 和表E2 所示。

表3 物理设备可靠性参数Table 3 Reliability parameters of equipment in physical system

表4 不同等级保电方案对应的模型计算参数Table 4 Calculation parameters according to different ranks of power emergency scheme

4.2 设备发展型故障率计算

根据中国某地区配电网2021 年设备运行工况统计数据，配电变压器、电缆线路和开关设备的发展型故障率计算参数如附录E 表E3 所示。结合该数据，运用2.1 节中设备发展型故障状态转移模型计算得到设备发展型故障率，将其与设备发展型故障率统计数据对比，结果如表E4 所示，偏差比均小于0.5%，验证了该模型的有效性。

在缺陷诊断周期不变（T0，d=30 d）的前提下，改变消缺比得到3 类设备的发展型故障率与系统平均供电可用率指标（average service availability index，ASAI）如附录E 图E1 和图E2 所示。在消缺比不变（β=80%）的前提下，改变缺陷诊断周期得到3 类设备的发展型故障率与系统ASAI 如图E3 和图E4所示。

由附录E 图E1 可知，随着消缺比的不断提升，3 类设备的发展型故障率均有所下降。如式（2）所示，运维检修人员的消缺比与设备缺陷消除率呈正相关关系。因此，提升消缺比能够同步提升设备缺陷消除率，降低设备处于故障状态的概率，使设备发展型故障率得以降低。此外，由图E2 可知，由于设备发展型故障率降低，系统可靠性得到改善。当消缺比由50%提升至100%时，ASAI 由99.991 03%提升至99.993 15%。缩短缺陷诊断周期有利于及时发现并消除缺陷，防止设备由缺陷状态发展为故障状态。因此，如图E3 所示，缩短缺陷诊断周期，3 类设备的发展型故障率均有所下降。此外，由图E4 可知，由于设备的发展型故障率降低，系统可靠性得到改善。当缺陷诊断周期由60 d 缩短至5 d 时，ASAI 由99.979 77%提升至99.999 44%。

综上所述，可以通过以下措施降低设备发展型故障率、提高系统可靠性：1）加强运维检修人员的专业技能培训，提升消缺比；2）缩短设备缺陷诊断技术作用周期，及时查缺、消缺。

4.3 破坏型故障率计算

配电变压器、线路和开关设备的风险排除率和风险诊断周期如表5 所示。

表5 设备破坏型故障率计算参数Table 5 Parameters for equipment destructive fault rate calculation

结合该数据，运用2.2 节中设备破坏型故障状态转移模型计算得到设备破坏型故障率，将其与设备破坏型故障率统计数据对比，结果如附录E 表E5至表E8 所示，偏差比均小于3%，验证了该模型的有效性。

在风险预警周期不变（Tr，0，l=8 h）的前提下，改变消缺比得到3 类设备的发展型故障率与ASAI，如附录E 图E5 和图E6 所示。在风险排除率不变（Ql=85%）的前提下，改变风险预警周期得到3 类设备的发展型故障率与ASAI，如图E7 和E8 所示。由图E5 可知，随着风险排除率的不断提升，3 类设备的破坏型故障率均有所下降。由式（15）和式（16）可知，运维检修人员的风险排除率与风险抑制率呈指数正相关关系。因此，提升风险排除率能够同步提升设备风险抑制率，降低设备处于故障状态的概率，从而使设备破坏型故障率得以降低。此外，由图E6 可知，设备破坏型故障率得以降低，系统可靠性得到改善。当风险排除率由45%提升至95%时，ASAI 由99.991 14% 提升至99.993 27%。由于缩短风险预警周期有利于及时发现并排除设备所处环境中破坏型风险因素，防止设备由风险状态发展为故障状态。因此，如图E7 所示，缩短风险预警周期，3 类设备的破坏型故障率均有所下降。此外，由图E8 可知，由于设备的破坏型故障率降低，系统可靠性得到改善。当风险预警周期由24 h 缩短至2 h后，ASAI 由99.977 50%提升至99.999 53%。

综上所述，可以通过以下措施降低设备发展型故障率、提高系统可靠性：1）加强运维检修人员的设备安全风险防范意识，提升风险排除率；2）缩短设备风险预警技术作用周期，及时告警。

4.4 故障恢复时间计算

根据2.3 节中的故障恢复时间模型，在故障定位技术覆盖的前提下，各类设备在不同技术精度下的故障定位时间如附录E 表E9 所示。

将保障点到保障范围内设备的平均距离控制在5 km，运维检修车辆的平均行驶速度为60 km/h，不同路况因子对应的平均路程时间如附录E 表E10 所示，算例中各保障点到保障范围内各设备的路程时间计算结果详见附录D。

各类设备在不同应急物资充裕度水平下的平均维修时间如附录E 表E11 所示。

由附录E 表E9 至表E11 中的计算结果可知：1）故障定位时间与故障定位技术精度有关，提升技术精度能较为有效地缩短故障定位时间，当精度达到95%时，故障定位时间可以缩短到5 min 以内；2）路程时间受路况因子的影响，路况因子越大表示道路越拥堵，对应的路程时间也越长；3）维修时间与应急物资充裕度相关，提升各保障点的物资充裕度能够缩短故障维修时间。

综上所述，可以通过以下方式缩短设备故障恢复时间、提高系统可靠性：1）提升故障定位技术精度，缩短故障定位时间；2）选择路况较好的道路通行，缩短路程时间；3）改善保障点物资配备情况，缩短维修时间。

4.5 配电网可靠性评估

不同保电等级间在运维检修人员的业务水平、设备的信息化程度等方面存在差异，导致模型参数不同，参数包括消缺比、缺陷诊断周期、风险排除率、风险诊断周期、故障定位技术精度、物资充裕度。本节分别列举4 种保电等级对应的模型参数、设备故障率及各类设备平均故障恢复时间计算结果，将计算结果作为输入参数运用解析法计算系统可靠性，各负荷点可靠性指标解析计算结果详见附录C。

不同保电等级对应的设备故障率、恢复时间计算结果如表6 所示，不同保电等级下的系统可靠性指标计算结果如表7 所示。

表6 不同保电等级对应的设备故障率与恢复时间Table 6 Equipment fault failure rate and recovery time according to different ranks of power emergency scheme

表7 不同保电等级下的系统可靠性指标Table 7 System reliability indices according to different ranks of power emergency scheme

对比表6 和表7 的数据可知，普通保电方案对应的消缺比、风险排除率以及故障定位技术精度最低，缺陷与风险诊断周期最长。在此情况下，设备的故障率大、故障恢复时间长，对应的系统可靠性最低。系统可靠性随保电等级依次升高，当采用特级保电方案时，系统可靠性最高。

5 结语

本文在传统配电网可靠性评估方法的基础上考虑了信息、社会系统对降低设备故障率、缩短设备故障恢复时间所起到的作用，提出了融合信息物理社会因素的配电网可靠性评估模型。

首先，通过构建设备发展型、破坏型故障状态转移模型量化了信息系统中缺陷及风险诊断周期、故障定位技术精度以及社会系统中运维检修人员的消缺比、风险排除率与设备故障率之间的关系。其次，通过构建设备故障恢复时间模型量化了社会系统中交通路况、保障点应急物资充裕度与设备故障恢复时间的关系。最后，建立了测试系统验证了模型的有效性。计算结果表明，改善信息、社会系统中的各项因素能够优化设备可靠性参数，从而对配电物理系统可靠性的提升起到支持作用。此外，本文所述方法分析了保电等级与系统可靠性的对应关系，有助于在重大社会事件背景下设置科学合理的保电方案。

在后续研究中，应结合工程实际，探寻信息系统中各项技术覆盖度、社会系统中存在的不确定性对配电物理系统可靠性的影响，进一步完善配电网CPSS 的可靠性建模。此外，本文的研究对象为电压等级为10 kV 的城市核心区配电网，包含开关、变压器和电缆这3 类设备，在此类配电网中，新能源与储能的渗透率相对较低，且配电线路多采用电缆线路。因此，仅考虑了上述3 类设备。在未来新能源高比例接入下，还可以进一步考虑架空线、分布式电源等设备，运用本文所提出的可靠性评估方法计算对应的系统可靠性。

附录见本刊网络版（http：//www.aeps-info.com/aeps/ch/index.aspx），扫英文摘要后二维码可以阅读网络全文。