中学数列的数学思想及其教学启示

欧慧谋，黄红梅，曹广福

中学数列的数学思想及其教学启示

欧慧谋1，2，黄红梅1，曹广福1

（1．广州大学 数学与信息科学学院，广东 广州 510006；2．韩山师范学院 数学与统计学院，广东 潮州 521041）

数学思想对学生的数学学习与未来发展具有深远影响．数学教学应在强调知识的同时，充分挖掘蕴藏在知识背后的数学思想，并在教学中通过针对性问题促使学生领会．中学数列的数学思想包括函数思想、递归思想、由特殊到一般、数学归纳法、消项求和思想以及极限思想等方面．基于中学数列的数学思想，提出如下教学启示：问题驱动概念教学，促进数列概念本质理解；从函数的角度审视数列，揭示两者的内在关系；重视递推公式教学，培养递归思维与发现能力；强化数学归纳法，拓展数学论证能力；诱发数列求和“好念头”，渗透消项求和思想．

数列；数学思想；教学启示

1 研究背景

什么是教育？爱因斯坦认为：“把在学校里学到的所有东西全部忘光之后留下来的东西才叫教育．”他的意思是，教育的核心价值并非知识的传授，而在于思想与方法的领悟以及观念与能力的提升．爱因斯坦的观点在数学教育领域有极大的共鸣，R·柯朗在批评过分强调数学公理化风气时曾指出：“创造发明的要素以及起指导和推进作用的直观要素，虽然常常不能用简单的公式来表述，但是它们却是任何数学成就的核心．”[1]米山国藏则认为：“作为知识的数学出校门不到两年就忘了，唯有深深铭记在头脑中的数学精神、数学思想、研究方法和着眼点等，这些会随时随地发生作用，使人终身受益．”[2]中国学者郑毓信持类似观点，认为：“数学教学应当努力提升学生的思维品质，由理性思维逐步培养学生的理性精神．”[3]这些观点无不说明，数学教学不能一味地追求数学知识，而应在强调数学知识的同时，促使学生获得相应的、对未来数学学习与自我发展影响深远的数学思想．

作为数学的重要概念，数列在现代数学的发展过程中发挥了重要作用．它既是数的拓展，又与函数关联；既是极限的载体，又是级数的基础；既在微积分中具有举足轻重的作用，又对实分析与泛函分析产生了深远的影响．弗赖登塔尔曾言：“无论从历史的、发生的还是从系统的角度看，数的序列都是数学的基石，没有数的序列就没有数学．”[4]数列“基石”的意义不仅体现在知识层面，还应包括蕴含在知识背后的数学思想．中学数列主要涉及等差数列与等比数列两类重要数列，内容虽然不多，但它们及其蕴含的数学思想，却是研究一般数列、级数以及大学相关数学知识的基础，也是进一步提升学生数学核心素养的重要载体．因此，教师不仅要关注数列知识，更要深刻认识数列的数学思想，这样才能批判性地分析教材，合理设计教学．

2 中学数列内容的编排特点

《普通高中数学课程标准（2017年版2020年修订）》（简称《课标》）将数列内容安排在选择性必修课程“函数主题”部分．《课标》要求[5]，教学应帮助学生通过对日常生活中实际问题的分析，了解数列的概念；探索并掌握等差数列和等比数列的变化规律，建立通项公式和前项和公式；能运用等差数列、等比数列解决简单的实际问题和数学问题，感受数学模型的现实意义与应用；了解等差数列与一元一次函数、等比数列与指数函数的联系，感受数列与函数的共性与差异，体会数学的整体性．至于数学归纳法，《课标》则降低要求，仅把其列为选学不考内容．

各个版本教材根据《课标》要求编写，体现较大共性，这里仅以人教版为例分析[6]．在内容安排上，教材首先介绍数列的概念及其表示方法，接着把重点放在等差数列与等比数列，最后介绍数学归纳法，体现由特殊到一般、循序渐进、主次分明的编排特点．在情境创设上，教材在概念的学习中创设了丰富的生活实例，包括年龄身高、月亮可见数、天坛石板、衣服尺码、海拔气温、细胞分裂、银行贷款等，这为学生认识数列提供了良好的条件．在逻辑推导上，非特殊数列（即非等差数列或者等比数列）的通项公式与递推公式主要由特殊到一般地观察发现，而特殊数列（即等差数列与等比数列）的通项公式与求和公式则通过推导得到．特别地，教材尤其注重从函数角度认识数列，不仅从离散函数的角度介绍数列，甚至通过解析式（即通项公式）、列表以及图象等方式表征数列；在等差数列与等比数列章节，教材还分别详细介绍了各自通项公式与一次函数、指数函数的关系．数学归纳法则作为证明数列命题的工具被引入，安排在数列最后一节．

显然，《课标》作为教学指导性文件，侧重数列知识的目标要求与教学指导，没有明确提出数列知识蕴含哪些数学思想，更没有告诉教师教学中如何渗透这些思想．而教材出于知识系统性、严谨性以及简洁性的考量，同样没有告知数学思想．例如教材在推导数列通项公式时，尽管遵循“由特殊到一般”的发现路径，但教材对此没有明说；类似地，教材虽然介绍了递推公式，但仅是蜻蜓点水，学生难以体会蕴含其中的递推思想．《课标》与教材的分析无不说明，与显性的数列知识相比，数列蕴含的数学思想具有隐性特征．这意味着，教师在备课与教学过程中，不应局限于《课标》，更不应把教材奉为“圣书”，而要深入数列知识的本质与来龙去脉，精准挖掘相关的数学思想，并在教学中加以渗透，这是实现真正数学教育的条件．

3 中学数列蕴含的数学思想

在梳理数列发展历史的基础上，综合分析数列概念、递归特点、通项推导、求和思维、变化趋势以及这些因素的内在逻辑关系，归纳出如下6个数列数学思想：函数思想、递归思想、由特殊到一般、数学归纳法、消项求和思想以及极限思想．

3.1 函数思想

3.2 递归思想

递归思想指在某个推导过程中，后续的每一步都需要前一步或前几步的信息与结果，这是一个从初始值开始，按照某种规律推导任意项的基本方法．递归思想并不遥远，项武义曾指出：“自然数系的本质就是一个按顺序排列的体系，起始者为1，往后每个数比其前一个数多加1，如此逐个加1以至于无穷；自然数系的加、乘和乘方运算都是由最原始的‘+1’运算逐步复合得到的．”[8]

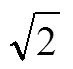
3.3 由特殊到一般

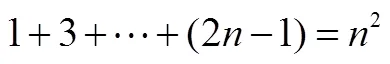
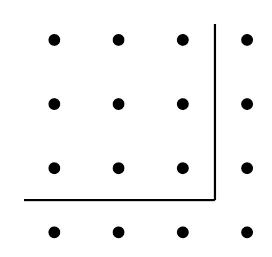
图1 正方形数

伽利略曾在长期观察行星运行的基础上，依靠天文数据近似得到椭圆运动定律．牛顿与莱布尼兹所创立的微积分则是前人关于切线、最值、速度以及面积等具体问题的一般化结果．凸多面体的欧拉定理、费马大定理、哥德巴赫猜想等同样源于对特殊情况的考察．正如拉普拉斯所言：“即使在数学里，发现真理的主要工具也是归纳和类比．”由特殊到一般甚至可以延伸到日常生活，所谓经验无非是在多次实践后的反思性认识．从这个角度看，由特殊到一般的思维方法是每个人必备的基本素养．

3.4 数学归纳法

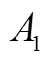
数学归纳法从其诞生起就与数列命题结下不解之缘．前述“正方形数”的研究可看成数学归纳法思想的源泉，但其本质上属于不完全归纳，缺乏严谨性．1575年，莫罗利科巧妙利用递推关系证明“正方形数”，即

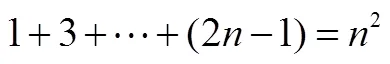
并总结出证明类似命题的步骤．因这种方法与通常的归纳程序相似，且主要用于证明数学命题，后来奥古斯塔斯·德摩根把其称为数学归纳法．

数学归纳法源于数列但超越数列，它在证明恒等式、不等式、数的整除、杨辉三角数、凸多边形内角和公式、凸多面体欧拉定理等与正整数有关的命题时，发挥着无可代替的作用，因而是一种重要的数学论证方法．正如R·柯朗所言：“与亚里士多德的基本逻辑规则（即演绎推理‘三段论’）那样，数学归纳法是数学的基本逻辑原则，每个学习数学的人，都应该掌握这种证明方法．”[1]这充分说明，新版教材增加数学归纳法是正确的．

3.5 消项求和

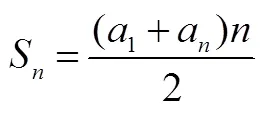
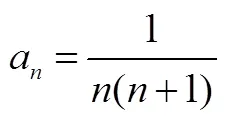
“消项求和”实际上是“降维思想”的一种具体形式，后者指把高维空间、高次方程、多元方程组、高维数据问题分别转化为低维空间、低次方程、一元方程、低维数据问题从而解决问题的一种基本思想．“降维思想”在高维、多元、多变量等复杂问题中具有重要意义．以数据分析领域为例，人们经常要在不改变高维数据结构的前提下对数据作降维处理，以建构更具扩展性、通用性的数据模型．在数列教学中，教师应通过“消项求和”的学习促使学生进一步认识“降维思想”．

当然，数列求和的途径并不是唯一的，还有其它途径可循，“数形结合”就是其中之一．前述毕达哥拉斯学派利用“形数”求解数列之和就是其中代表，中国数学家沈括、杨辉、朱世杰同样通过“垛积术”得到了诸如

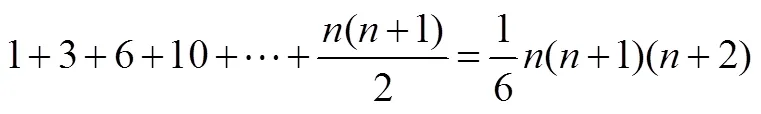
等数列求和公式[12]．因为“数形结合”不是中学数列求和的主流，这里暂且不做过多讨论．

3.6 极限思想

4 教学启示

数学思想具有潜在的、隐性的特征，把这种潜在的、隐性的数学思想转化为学生内在的个性素质还需要通过教与学活动来实现[14]．而问题是沟通数学知识与数学思想的桥梁，在数列教学中，教师应立足数列教学思想，设计针对性问题，激发学生数学思考，促使学生领会数学思想魅力．

4.1 问题驱动概念教学 促进数列概念本质理解

教材在引入数列、等差数列与等比数列概念时，虽然创设了丰富的生活实例，但缺乏具体的、指向性的问题．以数列的概念为例，教材提供了表1所示3个情境，但情境并没有嵌入任何具体问题，而是给出各自数据的关键信息——按照确定顺序排列，供学生分析学习，并通过问题“上述例子的共同特征是什么”引导学生抽象概括，得到数列的概念．从概念抽象的角度看，这种安排具有一定的合理性．但是，教材直接罗列与分析数据，替代了本可以由教师在课堂上引导学生进行的分析与思考，这将削弱培养学生数学思维能力的效率，不利于学生深度认识数列概念的函数本质．类似的情况同样存在于等差数列与等比数列概念，例如教材虽然通过4个具体情境引入等差数列概念，却没有设计合适的问题引导读者进一步思考其本质（等差递推关系），而且某些数列有人为编造痕迹，缺少一定的真实性．

表1 数列概念学习情境

问题是数学概念与原理的源泉，应是数学概念与原理的教学起点．张奠宙认为：“问题驱动的本质是暴露数学的本质，把数学‘冰冷的美丽’转化为‘火热的思考’．教师在介绍基本概念、基本理论、基本定理时，不能满足于形式地、演绎地给出，而要把数学本质用问题的形式揭露出来．”[15]在数列概念教学中，教师不妨结合数列历史、本质以及学生经验，寻找促使数列概念产生的本原性问题，以激发学生火热的思考，促进数列概念本质的理解[16–17]．例如，在引入数列概念与等差数列概念时，教师可分别创设如下问题．

问题1 刘徽的割圆术是说用圆的内接正多边形去逐步逼近圆，他从圆内接正六边形出发，将边数逐次加倍，边数越多，正多边形面积越接近圆面积．求半径为的圆内接正6边形的面积？当分别取1，2，3，…时，得到什么结论？

数学概念或原理的形成可以是源于现实生活、自然与工程或数学本身的问题，只要是具有启发性、本原性、触及数学本质、能够在教学中起统帅作用的问题都是好问题、真问题[18]．既然学生在“数列的概念”一节已初步学习递推公式，而它又是刻画等差数列的工具，教师不妨在此基础上创设数学情境，通过递推公式引入等差数列．

当然，为丰富学生对数列概念的认识，教师可以在以上问题的基础上，适当补充生活实例．

4.2 从函数的角度审视数列 揭示两者的内在关系

教材通过解析式、图象、表格等多元表征介绍了数列与函数、等差数列与一次函数以及等比数列与指数函数的内在关系，但缺乏深层次内在关系的探讨，例题或者习题也甚少涉及函数思想．由此导致的可能结果是，学生尽管知道数列是一类特殊的函数，却不清楚为什么要把数列看成函数，更不清楚寻找两者关系的真正价值．事实上，连续函数离散化是从抽象到机械化实现的必经之路，数值计算的前提便是离散化．将数列看成特殊的函数以及在函数的定义域中取特殊的点从而形成一个数列（大多数情况下是根据节点数确定步长），进而将连续函数离散化以便机械化处理，此重要思想方法是人机对话得以实现的基础．

从理论角度介绍数列与函数的内在关系是必要的，但理论有余、实践缺乏的教学不利于学生深入认识二者关系．教师需要适时引导学生从函数的角度审视数列问题，寻找数列与函数之间的关系，进而借助函数模型的性质解决问题，体会函数思想在数列问题解决中的魅力．

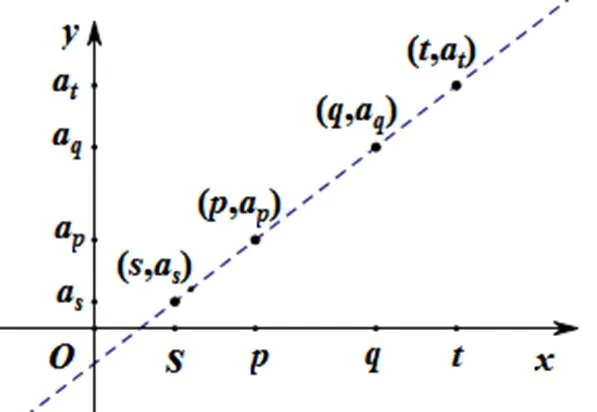
图2 问题1函数图象

结合二次函数性质（如图3所示），易可得的最大值为．

需要指出的是，教材从函数的角度介绍了数列的概念以及等差数列与等比数列的通项公式，但没有明确等差数列与等比数列前项公式的函数属性．数列求和是数列应用的焦点，数列和的最值、单调性等是人们经常需要解决的问题，这也是函数的重要问题，这些问题可以统一起来，利用函数的性质加以解决．因此，在介绍等差数列与等比数列前项公式时，教师不妨分别从二次函数与指数函数的角度加深认识．

4.3 重视递推公式教学 培养递归思维与发现能力

但是，递推公式是教学难点，教学很容易陷入复杂的细节与技巧的纠缠，导致学生产生恐惧心理．通项公式与递推公式是表示数列的两个重要工具，二者最大的不同在于，前者是数列的函数解析式，后者则是从递推角度表示数列的模型．递推公式本身具有很好的生活化情境认知基础，教师给出递推公式定义后，可以适当创设生活情境，丰富学生对递推公式的认识，体会递归思想．由递推公式推导通项公式时，宜引导学生学会由特殊到一般地发现规律，提升归纳与猜想的数学能力．

问题1 阶梯形剧场第一排有20个座椅，后面每排比前排多1个座椅，剧场共有20排座椅，剧场各排座椅数构成的数列能否用递推公式表示？

问题2 数学家斐波那契在观察兔子繁殖时，提出一个有趣的问题：如果1对兔子每月生1对小兔子（一雄一雌），而每对小兔子在它出生后的第3个月里，又生1对小兔子，假定在不发生死亡的情况下，由1对初生的小兔子开始，50个月后会有多少对兔子？

当然，依据递推公式推导通项公式，除由特殊到一般途径外，还有其它方法．例如，由斐波那契数列的递推公式推导其通项公式的方法有多种，而适合中学生的初等方法是利用递推关系构造一个新的等比数列[20]．

4.4 强化数学归纳法 拓展数学论证能力

数学归纳法属于选修不考内容，但鉴于它的重要性，高中生学习数学归纳法是必要的．一方面，高中生无论是辩证思维还是知识储备都有了长足的发展，完全有能力学好、用好数学归纳法．另一方面，介绍数学归纳法是国际数学课程的普遍要求[21]，新加坡H2数学考试（相当于中国理科高考数学）甚至经常考查学生利用数学归纳法证明数列命题的能力[22]．中国虽然对此没有考试要求，但如果学生了解数学归纳法，在遇到数列等与正整数有关的问题时，至少可以减少直觉错误，甚至多一种求解选择．

与其探讨要不要介绍数学归纳法，不如探讨怎么教授数学归纳法．教材在给出等差数列通项公式后，没有直接证明公式，而是通过分析多米诺骨牌游戏类比介绍数学归纳法，最后才回头利用数学归纳法进行证明．数学归纳法主要源于数学问题，而不是多米诺骨牌游戏，教材通过多米诺骨牌游戏直接介绍数学归纳法是否合理，有待商榷．弗赖登塔尔在批评数学归纳法教学时就曾指出：“学习数学归纳法的正确途径是向学生提出一些必须用数学归纳法才能解决的问题，迫使学生直观地使用这个方法，从而发现这个方法．”[4]依其观点，通过数列问题介绍数学归纳法或许更合适．当然，这并非否定多米诺骨牌游戏的意义，事实上，给出数学归纳法定义后，教师有必要把其基本步骤与多米诺骨牌游戏进行类比．

问题2 数学归纳法可靠吗？你能否类比多米诺骨牌游戏说一说其可靠性？

问题3 归纳推理与数学归纳法有何异同与关联？

以上问题层层递进，共同促进学生发现、认识、应用数学归纳法．其中，问题1可以促使学生在通项公式的证明中发现数学归纳法，同时揭示学习数学归纳法的缘由．问题2意在引导学生类比多米诺骨牌游戏，直观认识数学归纳法，消除可靠性疑虑．问题3有助于启发学生厘清归纳推理与数学归纳法的关系，凸显数学归纳法的演绎推理属性．另外，教材关于数学归纳法的应用仅限于数列命题，这容易使学生产生“数学归纳法只能证明与数列有关命题”的错觉，问题4恰好可以弥补教材遗憾．

4.5 诱发数列求和“好念头” 渗透消项求和思想

教材分别通过“倒序相加法”与“错位相减法”推导等差数列与等比数列前项和公式，从纯数学推导的角度看，学生对这些方法不存在认知上的困难，他们甚至对方法之巧妙赞叹不已[24]．但这样的方法是如何想到的？学生往往不明所以．在他们眼里，这些方法犹如从帽子里跳出来的兔子，突兀得让人不知所以然．如果教师对此没有足够的思考与措施，教学容易纠缠于技巧与细节．波利亚认为，数学解题的关键在于诱发“好念头”[25]．教师不妨从数列求和的矛盾与思想出发，诱发学生对数列求和产生“好念头”．

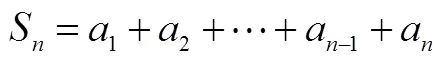
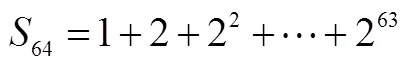
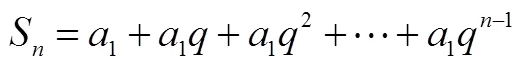
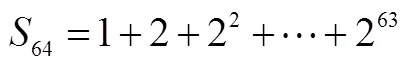
问题1 这是一个什么问题？怎么求解？

问题2 前面用什么方法推导等差数列的前项求和公式？它可以用来计算该问题吗？

问题3 虽然“倒序相加法”无法直接计算该问题，但从中能否得到什么启发？

5 结束语

教育的全部目的就是使人具有活跃的智慧[26]．数学知识并非不重要，事实上它是学生发展必不可少的基础．然而，停留在数学知识传授的教学不是真正的数学教育，那种只灌输数学知识、忽略数学思想的教学，既不利于学生理解数学的本质，也无法激发对数学火热的思考，更无助于学生的自我发展．数学教学应揭示发现、建构数学知识的一般策略与方法，增强学生主动建构、创造数学知识的意识与能力，这样才能使数学核心素养落到实处[27]．

但是，数学思想的隐性特征要求教师深入认识数学知识的本质与来龙去脉，精准挖掘数学知识背后的数学思想，这样才能设计科学合理的教学方案，引导学生在数学知识的形成与发展过程中领会相关的数学思想．另一方面，学生对数学思想的领会是一个循序渐进的过程，不可能一蹴而就，教师需要通过不同数学知识的教学有意识地加以渗透．显而易见，数学思想对学生数学学习与未来发展的影响是一个长期的、潜移默化的过程．

[1] R·柯朗，H·罗宾．什么是数学[M]．左平，张饴慈，译．上海：复旦大学出版社，1995：3．

[2] 米山国藏．数学的精神、思想和方法[M]．毛正中，吴素华，译．上海：华东师范大学出版社，2019：序1–2．

[3] 郑毓信．数学思维教学的“两阶段理论”[J]．数学教育学报，2022，31（1）：1–6，78．

[4] 弗赖登塔尔．作为教育任务的数学[M]．陈昌平，唐瑞芬，译．上海：上海教育出版社，1995：160．

[5] 中华人民共和国教育部．普通高中数学课程标准（2017年版2020年修订）[M]．北京：人民教育出版社，2020：38．

[6] 人民教育出版社课程教材研究所．普通高中教科书·数学选择性必修第二册[M]．北京：人民教育出版社，2020：1–57．

[7] 莫里斯·克莱因．古今数学思想（第一册）[M]．张理京，译．上海：上海科学技术出版社，2014：308–309．

[8] 项武义．基础代数学[M]．北京：人民教育出版社，2004：5–8．

[9] 李昌官．递推：数列的灵魂[J]．数学通报，2018，57（10）：22–25．

[10] 胡国定．简明数学词典[M]．北京：科学出版社，2000：557．

[11] 涂荣豹．数学教学设计原理的建构——教学生学会思考[M]．北京：科学出版社，2018：130．

[12] 李文林．数学史概论[M]．3版．北京：高等教育出版社，2012：100–102．

[13] 卡茨．数学史通论[M]．李文林，译．北京：高等教育出版社，2018：88–89．

[14] 王道俊．知识的教育价值及其实现方式问题初探——兼谈对杜威教育思想的某些认识[J]．课程·教材·教法，2011，31（1）：14–32，43．

[15] 张奠宙，张荫南．新概念：用问题驱动的数学教学[J]．高等数学研究，2004（3）：8–10．

[16] 曹广福，张蜀青．论数学课堂教学与评价的核心要素——以高中导数概念课为例[J]．数学教育学报，2016，25（4）：17–20．

[17] 吕松涛，曹广福．高中向量教学中数学思想的渗透[J]．数学教育学报，2021，30（4）：19–24．

[18] 王海青，曹广福．问题驱动数学教学的基本原则与思想及其实施步骤[J]．数学教育学报，2022，31（1）：24–27．

[19] 李子瞻，胡典顺．基于数学核心素养的新旧高考比较分析——以2021年新高考Ⅰ卷与2020年全国Ⅰ卷为例[J]．数学教育学报，2022，31（3）：26–31．

[20] 曹广福，张蜀青，欧慧谋．问题驱动的中学数学课题教学（函数与微积分卷）[M]．北京：清华大学出版社，2022：35．

[21] 王科，汪晓勤．“中美日新”四国高中教材中的数学归纳法比较研究[J]．数学教育学报，2015，24（2）：40–45．

[22] Singapore ASIA Education. Past examination papers arranged by year 2011—2020: A level h2 mathematics yearly edition [M]. Singapore: Singapore Asia Publishers Pte Ltd, 2021: 不详.

[23] 张雄，李得虎．数学方法论与解题研究[M]．2版．北京：高等教育出版社，2003：54．

[24] 张蜀青．数列教学中的数学思想之光[J]．数学通报，2021，60（2）：45–48．

[25] 涂荣豹．数学解题学习中的元认知[J]．数学教育学报，2002，11（4）：6–11．

[26] 怀海特．教育的目的[M]．徐汝舟，译．北京：生活·读书·新知三联书店，2022：66．

[27] 李昌官．数学发现与发明关系新说[J]．数学教育学报，2022，31（1）：97–102．

The Mathematical Thoughts of Number of Sequence in Middle School and Its Teaching Enlightenment

OU Hui-mou1, 2, HUANG Hong-mei1, CAO Guang-fu1

(1. School of Mathematics and Information Science, Guangzhou University, Guangdong Guangzhou 510006, China;2. School of Mathematics and Statistics, Hanshan Normal University, Guangdong Chaozhou 521041, China)

Mathematical thoughts have a profound impact on students’ mathematical learning and future development. Mathematics teaching should not only emphasize knowledge, but also fully excavate the mathematical thoughts behind knowledge, and promote students’ understanding through targeted questions during teaching. The mathematical thoughts of number of sequence in middle school include function thought, recursion thought, from special to general, mathematical induction, elimination and summation thought, limit thought, etc. Based on the mathematical thoughts, the following teaching implications of number of sequence are proposed:problem-driven concept teaching promotes understanding of the essence of sequence concept; examines the sequence of numbers from the perspective of function to reveal the internal relationship between them; pays attention to the teaching of recursive formulas to cultivate recursive thinking and discovery abilities; emphasize mathematical induction to expand mathematical argumentation capabilities; and induces the good idea of summation of the sequence to infiltrate the elimination and summation thought.

sequence of number; mathematical thoughts; teaching enlightenment

G632.0

A

1004–9894（2024）01–0001–07

欧慧谋，黄红梅，曹广福．中学数列的数学思想及其教学启示[J]．数学教育学报，2024，33（1）：1-7．

2023–10–02

国家“万人计划”人才项目——问题驱动的数学课堂教学理论与实践；“粤港澳大亚湾国家应用数学中心”项目——问题驱动的中小学数学教育研究（2020B1515310020）；韩山师范学院教育教学改革项目——问题驱动视角下的数学教学研究（0006/E22110）

欧慧谋（1982—），男，广西玉林人，讲师，博士生，主要从事数学课程与教学论研究．曹广福为本文通讯作者．

[责任编校：周学智、陈汉君]