中美大学微积分教材之微分方程内容的比较研究

潘建辉，胡学刚，朱 伟，邓志颖，陈继林

中美大学微积分教材之微分方程内容的比较研究

潘建辉1，胡学刚2，朱 伟1，邓志颖1，陈继林3

（1．重庆邮电大学 理学院，重庆 400065；2．重庆邮电大学 教务处，重庆 400065；3．重庆市天星桥中学，重庆 400038）

对中美大学微积分5套教材中微分方程内容的比较研究发现，中美教材在内容的编排位置、习题数量、数学表征方式、数学软件的使用、对数学建模的偏重程度、对次要或较高要求内容的处理方式，以及微分方程模型解决的实际问题数量和类型等都存在差异．美国教材在数学建模的思想方法指导和数学建模难点突破方面，有许多做法值得借鉴．中国教材存在一个重大缺陷，就是求解“无初等解析解的微分方程”所需的大部分知识均未编入教材．由此得到3点启示：一是教材编写者对知识点的认识偏差可能会导致编写指导思想上的偏差；二是数学能力的培养和训练并非都是有益的；三是习题除了具有提供练习的显性功能外，还有许多隐性功能有待开发利用．针对同济教材，建议：增加方向场、欧拉方法等重要内容；删去高阶微分方程等过于形式化的内容；调整微分方程的幂级数解法等的编排位置．

大学教材；微积分；微分方程；比较研究；数学建模

1 问题提出

教材是学生自学、教师备课和课堂教学的核心资源和主要依据．高质量的教材是高质量教学的基本保障．因此，近年来，关于数学教材的研究在国际数学教育界受到越来越多的关注[1]，教材的比较研究自然也就成了历届国际数学教材研究和发展会议的重要课题之一[1-4]．另一方面，微积分是大学理、工、农、医、商科等重要的公共基础课程，对大学生的数学素养和能力的培养起着至关重要的作用．于是，随着中国高校数学教育改革的深入推进和中外数学教育交流的日益增多，关于大学微积分教材的比较研究也已日渐增多．然而，这些研究的现状如何，取得了哪些成果，还有哪些不足呢？

2 大学微积分教材比较研究的现状

中国学界，在大学微积分（高等数学）教材的比较研究中，除有零星的纵向比较研究外[5-11]，绝大多数都是中美教材横向的比较研究[7-14]．其中，除少数是从一个知识点的微观视角的比较研究外[7]，其余都是从整个微积分体系的宏观视角的比较研究[8-14]．此外，有学者还从习题配置特色[15]、数学史与数学教育[16]和先修计划课程[17]等角度，单独对美国微积分教材进行了研究．

（1）中美两国使用面最广和最著名的大学微积分教材．中国是同济版的《高等数学》，美国是James Stewart编写的《微积分》和George B. Thomas和Joel Hass等编写的《托马斯微积分》等教材[7-16]．

（2）中国大学微积分教材的特点．中国目前普遍使用的教材是在1950年代初学习前苏联模式的基础上几经修改形成的[5，6，9，13]；各版本教材的知识体系大的框架、编写的指导思想与风格趋于同质，显得僵化、陈旧、单一[6，9]；教材缺乏时代气息和知识的实际应用[9]；教材的编排遵循学科的逻辑顺序，结构紧凑，逻辑清晰，注重表述的形式化[7，10-11]；不少高校将配套的电子教材、PPT、教案等教学资源放在网上共享，但其中有新意、有亮点、坚持更新的不多[9]．

（3）美国大学微积分教材的特点．始于20世纪80年代的美国微积分教学改革运动，对美国的微积分课程与教材建设都产生了深远的影响[7]；美国教材内容的编排更多地遵循学生的心理顺序[7]；并以图形、数字、文字和符号四元表征并重[17]；重视概念的直观理解和物理背景[16]，打破严格的结构体系——结合学生的认知水平和历史顺序来组织教学内容[16-17]；形式生动，注重解决现实问题以及与其它学科的联系和现代信息技术的应用[7]；注重知识的产生过程和学习指导[7，8，10-11]；重视计算与作图软件的使用[10-11，17]．

（4）中国教材课后习题的特点．中国教材习题数量少、形式单一，从数学上加工得比较正规，以知识立意为主，立足于对所学知识进行复习、巩固和推广[7，15]；习题侧重于用数学定理和公式去解决纯数学问题，讲究解题技巧，应用问题主要涉及几何与物理领域，而数值计算、借助计算机作图及探索的习题几乎没有，难以使学生体会到微积分的应用价值和学习乐趣[8，10-11]．

（5）美国教材课后习题的特点．美国教材习题数量多，形式丰富，包括概念题、计算题、证明题，以及大量的应用题、讨论题和探索题[8-11，15]；每章末还有复习题、实践题、附加题，以及借助图形计算器和CAS的数值计算题和探索题等[11]；应用题内容丰富，涉及面广，很多来自于生活和科技实际，情景鲜活，数据真实[7-8，11，15]；教材提供立体化网络支持，包括授课视频、课件、常用数学网站链接、2D/3D在线绘图软件和交互式在线辅导等，让学生自主学习和探索实践，使课堂教学得以延伸[9]．

总体而言，以上关于中美大学微积分教材的评价基本准确、恰当，对中国大学微积分教材的修改与课程教学具有一定的参考和指导意义．然而，由于以上比较研究的视角过于宏观或微观，致使部分结论过于宽泛、笼统，甚至片面、失当．“同济七版的总体难度高于美国宾夕法尼亚九版”[8]的结论就过于宽泛、笼统，对教学无多大指导意义．“微分方程属于微分板块”[8]“我国教材比美国教材更注重逻辑或理论的严谨性”[7-9]，以及“中国教材课后练习设计，突出记忆、理解和应用的刚性过程，缺少分析、评价和创造的柔性过程”[7]等观点，都是值得商榷的．

因此，为了减少过于宽泛、笼统、表面、片面等情况的发生，下面拟从中美微积分教材中选取几套典型教材，并以典型章节的中观视角为基调，兼顾宏观和微观视角，对中美教材进行比较研究，以期得到更为具体、准确、深入的研究结论，供教材编写者和课程教学者参考．

3 中美教材中微分方程内容的比较

3.1 教材和内容的选取

（1）教材的选取．中国选取的是全国使用面最广的同济最新版《高等数学》[18]（简称同济教材）、中国大学MOOC有较大影响的国防科技大学最新版《高等数学》[19]（简称国科教材）和中国人民大学最新版《高等数学》[20]（简称人大教材），共3套．美国选取的是由James Stewart编写的、在美国使用面最广（占65%）[9，21]的最新版教材《微积分》[22]（简称Stewart教材）和由George B. Thomas，Joel Hass等编写、使用历史最长（从1951年开始[9-11]，至今已有14版）的最新版教材《托马斯微积分》[23]（简称Thomas教材），共2套．

（2）内容的选取．一方面，现实世界的问题，经常要涉及到变化的量，人们总是希望根据当前值的变化来预测未来的行为，这通常需要建立微分方程模型，而微分方程又是微积分中最重要的应用之一[22-23]．另一方面，微分方程在中美教材中的差异十分显著．通过对其进行比较研究，就能更多地找出两国教材设计背后所蕴含的教育思想、理念、方法上的差异，以便更好地指导研究者开发和利用教材，提高教学质量．

3.2 微分方程知识点的比较

3.2.1 微分方程的章节在中美教材中所处位置的比较

中美教材中，微分方程章节所在的位置差异巨大．中国教材都是在介绍完一元函数的微分和积分之后，将微分方程的内容集中编排在上册的最后一章内，而美国教材则是将其分散编排在三、四章之内的．

首先，Stewart教材和Thomas教材在介绍了原函数和积分曲线的概念后，将微分方程、解和通解等概念，分别排在了第四章的4.9节“不定积分”和4.7节“反导数（原函数）”里．这样，求微分方程的解函数和解函数图象，就相当于求原函数和积分曲线．这就将微分方程有关概念和解微分方程的方法，与原函数、不定积分，以及求不定积分的知识和方法很自然地联系和融合在了一起．

接下来，Stewart教材和Thomas教材都是在介绍了指数函数后，分别在第九章“微分方程”和第七章的7.4节“指数变化和可分离变量的微分方程”里，依次介绍指数增长、指数增长模型、可分离变量的微分方程等内容．Thomas教材到第九章才介绍一阶线性微分方程，而且这两部教材都是在介绍了无穷级数之后，直到全书末的第十七章才介绍二阶微分方程的内容．Thomas教材只列出了各小节标题，内容需登录网页才能阅读（相当于选学）．

由此可见，中国教材是按学科的逻辑顺序进行编排，而美国教材则是按学生的认知水平和知识的历史发展顺序进行编排的．这两种编排方式各有优缺点．美国教材将微分方程的知识有机地融入到微积分的发展历史中，使微分方程、解函数、解函数曲线、指数增长模型等概念的出现十分自然．但另一方面，由于微分方程的知识被分割得过细，分块数过多，这就使知识显得零碎、不够连贯．中国教材的编排方式，其优点是使微分方程的知识显得紧凑，也使得整个教材显得分块明晰、更有条理性；但其不足则是基本概念的出现没有美国教材那样自然，略显突兀．

3.2.2 微分方程的知识点及其处理方式的比较

中美教材中微分方程所包含的知识点及其处理方式也有很大差异．这5套教材处理知识点的方式有常规和非常规两类，常规类包括必修、选修、不修（缺少）3种，非常规类包括将其编入习题让学生通过练习来学习、放在网络平台上供学生在线学习、转移到其它章节以后学习3种．若将这6种方式依次简记为必、选、缺、习、线、转，则中美教材所含知识点及其处理方式的详情如表1所列．

为了弄清楚哪些处理方式更好，就必须弄清楚这章知识的逻辑体系和各知识点之间的相互关系（见图1）．从图1可以看出，虚线上侧内容，中美教材差异不大，下侧内容差异巨大．其差异具体体现在以下3方面．

中国教材编入正文，而美国教材编入习题或缺少的内容．这些内容有齐次方程、一阶非线性方程中的伯努利方程、可降阶的3类二阶微分方程和特殊的高阶微分方程．将它们编入正文会使教材显得知识体系更为完备，不编入正文则可节约教学时间，突出主干．两者各有利弊．但相比之下后者更好．为了突出重点，节约教学课时，将相对次要的内容编入习题或删掉，能起到淡化形式[24-25]、增强实效的作用．这是教材编写的一个技巧，值得借鉴．另外，解一阶线性非齐次微分方程，中美教材分别用的是常数变易法和积分因子法．后者比前者更好理解，公式更简单易记．相比之下，后者更好．

中美教材最大的差异在于如何处理“无初等解析解的微分方程”的内容．美国教材用了大量的篇幅来系统介绍该内容，而中国教材只涉及到两个知识点．一是“方向场”，仅国科教材有；二是“微分方程的幂级数解法”，仅同济和国科教材有，并且被降格为“幂级数的应用”而纳入“级数”一章[26-27]．

表1 中美微积分教材之微分方程知识点及其处理方式的比较

然而，是否有必要将该内容完整地编入教材呢？很有必要．这是因为，在解决实际问题时，所列的微分方程即使有解，也几乎没有初等的解析解，哪怕对于一个看起来简单的方程也是如此．如-2+= 0．但是，能够求解像这样的方程是很重要的，因为它们产生于物理问题，特别是与量子力学中的薛定谔方程有关[22-23]．既然所列的微分方程几乎没有初等的解析解，那么在解决实际问题时，图1中虚线上侧的解微分方程的所有方法几乎都会失效．学生把这些方法学得再好，几乎都不能解决实际问题，只能形式化地求解一些微分方程的习题．因此，在解决实际问题时，通常要用幂级数法求级数形式的解函数，用欧拉方法求初值问题的近似解，用方向场来分析解函数的大致图象，用相直线、相平面来分析自治方程和自治方程组的轨线、平衡解和解的稳定性等问题．故，未将“如何处理无初等解析解的微分方程”的内容完整地编入教材，是中国大学微积分教材的一大缺陷．

中美教材在列微分方程方面的差异巨大．列微分方程就是建立微分方程模型，属于数学建模的范畴．数学建模是数学核心素养之一，备受国际数学教育界的广泛关注[28-29]．因此，该内容将被合并到下一节加以重点讨论．

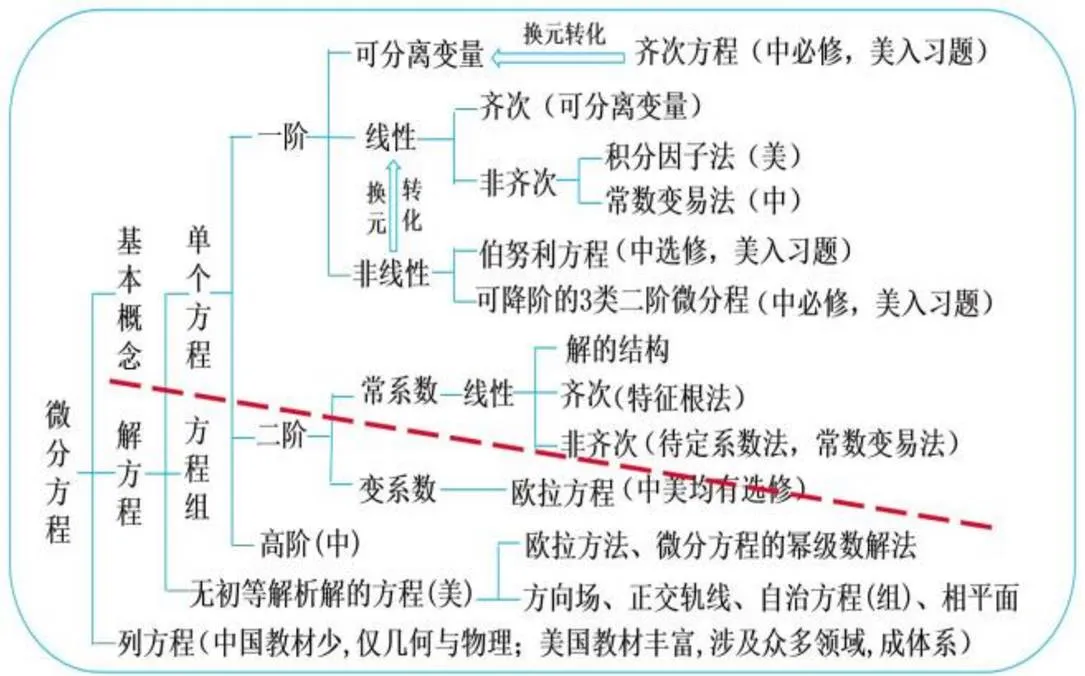
图1 微分方程的知识网络树状图

3.3 微分方程模型和数学建模方面的比较

3.3.1 数学模型所解决问题类型数的比较

经统计，中美教材中微分方程模型所解决的各类问题如表2所列．

由表2可知，微分方程模型解决的实际问题类型数，同济、国科、人大、Steward、Thomas教材依次为18、25、24、35和30（不含二阶方程）．同时，中国教材对每一类方程仅给出了1～2个需要列方程建模的实例；而美国教材一般都给出了若干个实例加以印证或练习．因此，美国教材用微分方程模型解决实际问题的数量大大超过中国教材．

3.3.2 微分方程所涉及的问题类型特点的比较

这5套教材中，Steward教材所包含的问题种类最多、最全面，不仅包含常见的运动问题、冷却问题、同位素衰减问题、溶液混合问题、RL电路问题、震动问题、病毒（消息、谣言）传播问题等，而且还包含追迹问题、捕食者—猎物问题、两个种群的竞争（合作）问题等．在微分方程模型方面，该教材最突出的特点就是其种群增长模型的种类较为齐全且成体系（见图2）．

Thomas教材，在不包括二阶微分方程的情况下，其中的问题类型总数仅次于Steward教材．关于种群增长的模型虽不及Steward教材的系统、全面，但指数增长模型所涉及的问题类型却相当丰富，共有16类之多．这些问题中，除含常见的运动问题、同位素衰减问题、冷却问题和种群增长问题外，还有疾病控制问题、细菌生长问题、粗糖融化问题、一阶化学反应问题、人类牙齿进化问题、电容器的放电问题、水下光线强度问题、濒危物种保护问题等．不仅如此，而且即使是同位素的衰减这一类问题，也包含了许多不同的案例．这些案例涉及到放射性同位素C-14、钚-239、钋-210、锎-252，以及它们的半衰期，平均寿命．仅根据C-14的衰减规律，就有多个考古鉴定问题．

国科教材与国内其它教材相比，虽然微分方程模型所涉及的问题类型较为全面，但与美国教材相比，其数量还是偏少．若增加疾病传播模型和捕食者—猎物模型，并适当丰富指数增长模型，则会更好．人大教材总体上与国科教材类似，只是缺少捕食者—猎物这个重要模型，且问题的总量明显偏少．同济教材在建模问题的选取和设计上，做得最不理想．一是问题类型总数严重偏少，比Stewart教材少了近50%．二是涉及的内容大多是几何与物理问题，而且不少还是较难的选学内容．如探照灯聚光面的设计、悬链线方程、链条下滑等问题，这些既是物理学中学生难以建模，又是被美国教材淡化处理的内容．三是该教材中还缺少许多常见问题．如冷却问题、谣言传播问题、种群增长问题、追迹问题、捕食者—猎物问题、两物种的竟猎问题等．因此，在教学实践中，使用同济教材的大多数教师，都很少讲解数学模型的建立，只讲如何求解各类微分方程．这是中国在微分方程这章教学上很大的一个偏差，需引起重视．

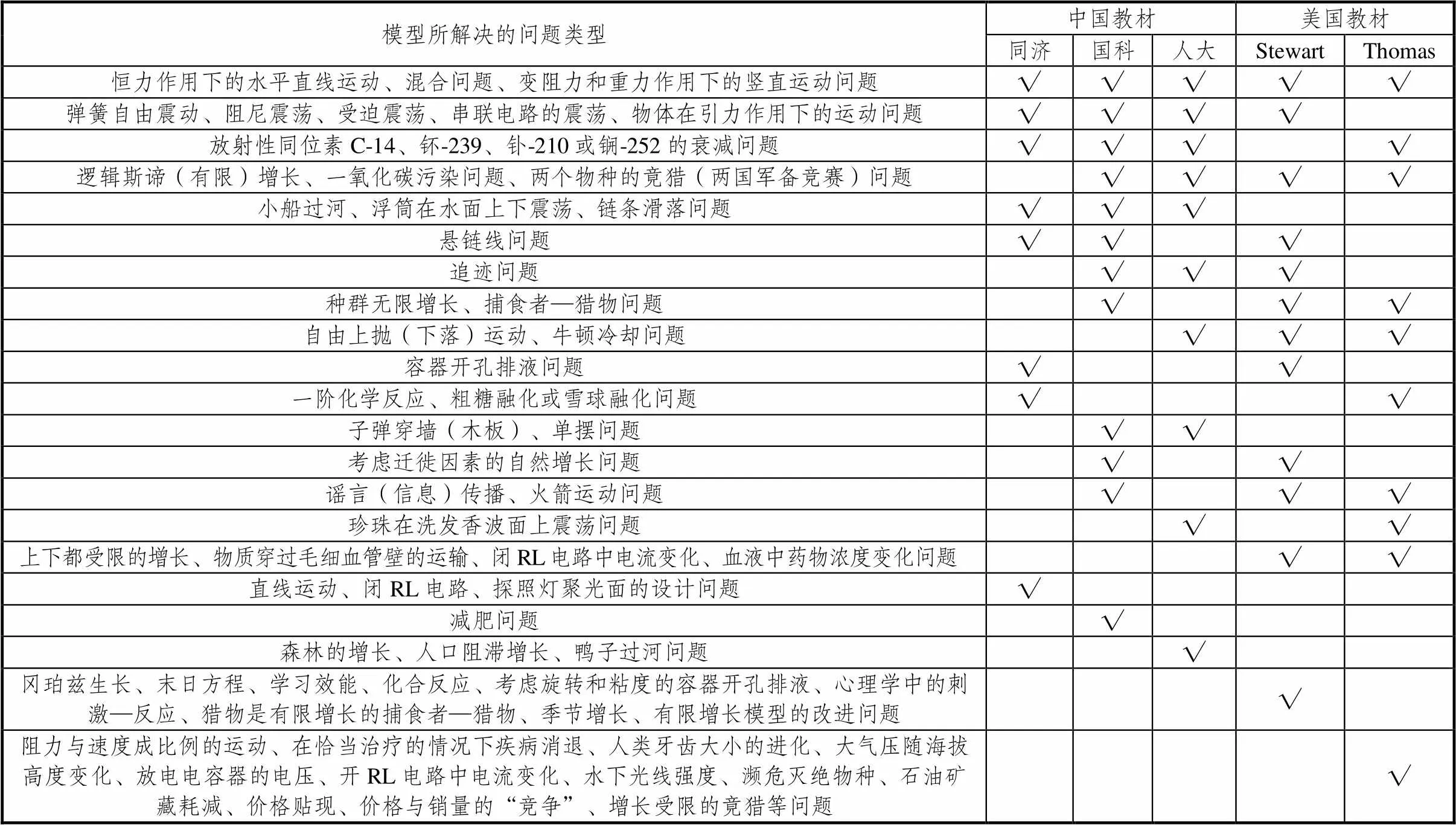
表2 中美教材中微分方程模型所解决的问题类型比较

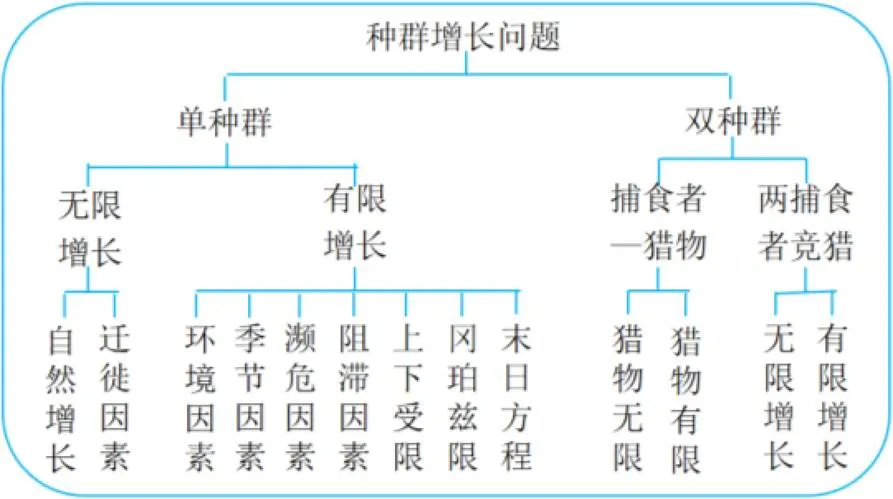
图2 Stewart教材中的种群增长模型体系

3.3.3 美国教材在数学建模思想方法上的指导和数学建模难点上的突破

美国教材在数学建模的思想方法指导和数学建模难点突破方面，有许多好的做法，值得借鉴．

（1）将大型主题的模型体系进行分解，然后分散到正文、例题、习题和应用项目等内容中．如Stewart教材中的种群增长的模型体系就十分庞大（图2）．其中不仅涉及到单种群和有互动关系的多种群问题，以及各种附加条件和变化的情形，而且还涉及到可分离变量方程、一阶线性非齐次方程、自治方程组等情形．即使是专门的数学建模课，也要花好几个学时才能完成．然而，该教材却巧妙地通过各个击破，层层推进，分散处理等技巧，很好地化解了这一难题．

（2）以应用项目的形式，使学生经历小型的数学建模过程，并获得数学建模思想方法的熏陶．如Stewart教材中的应用项目“讨论油箱排水的速度有多快”，其中就包含这几个问题：（a）根据托里切利定律，建立容器底部开孔排水问题的数学模型，然后根据给定数据，求多长时间可以排干；（b）给出考虑了液体的旋转与粘度因素的改进模型，然后进行下降高度与所用时间的对应关系实验，将实验结果与由模型算出的函数计算结果进行比较；（c）利用改进模型解决大型酒店和医院屋顶的喷水灭火系统的设计问题；（d）讨论非圆柱形的、截面积随高度变化而变化的一般容器的开孔排水模型．类似这样的项目，美国2套教材中都有不少．总之，以小型项目的方式，对学生进行数学建模思想方法的指导，这也是值得借鉴的．

（3）将数学建模中的思想方法渗透到习题中．这种方式在美国教材中十分普遍．如Stewart教材中，习题9.4的4题，根据酵母细胞数的实验室记录数据，描点作图、估计该实验环境的细胞数承载能力、初始增长率、建立指数模型和逻辑斯谛模型，并将由函数式得到的预测值与从表格中和图象上得到的值进行比较，评论所建模型与数据的匹配程度，用逻辑斯谛模型预测7小时后酵母细胞的数量；10题，讨论逻辑斯谛模型中两个参数分别变动时，解函数曲线如何变化；11题，用指数模型和逻辑斯谛模型的解函数曲线拟合表中给出的1960—2005年日本人口数量，并评价何者更精确；16题，讨论改进逻辑斯谛模型的参数在什么情况下才不至于使鱼灭绝；等等．这些习题中都大量渗透了数学建模的思想和方法．

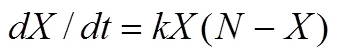
（5）对于部分较难建立的模型，教材是通过铺设“台阶”，逐步提问引导学生建立的．例如，Thomas教材中习题9.3的13题（盐水混合问题）条件是：一水箱最初装有100加仑含盐50磅的盐水，现将浓度为21磅/加仑的盐水以5加仑/分钟的速度注入其中．同时，将其搅匀后又以4加仑/分钟的速度排出水箱．如果直接问“混合过程开始后的第25分钟时，水箱内混合盐溶液的浓度是多少”，那么学生就会觉得很难求解．为此，该教材就给这一问题铺设了4级“台阶”：（a）在时刻，盐被注入水箱的速度（磅/分钟）是多少？（b）在时刻，水箱内溶液体积是多少？（c）在时刻，盐被排出水箱的速度（磅/分钟）是多少？（d）写出并求解描述本混合过程的初值问题的微分方程．这4级“台阶”实际上就是解决原问题的思维过程中的4个关键节点．这既是教师引导提问的技巧，又是铺设“台阶”，降低建模难度的技巧，值得借鉴．

3.4 教材的其它构成要素的比较

中美教材的主要差异，除了体现在内容的编排位置、知识体系和对数学建模的处理方式的不同之外，还体现在习题数量、软件使用和数学表征等方面．其详情如表3所列．

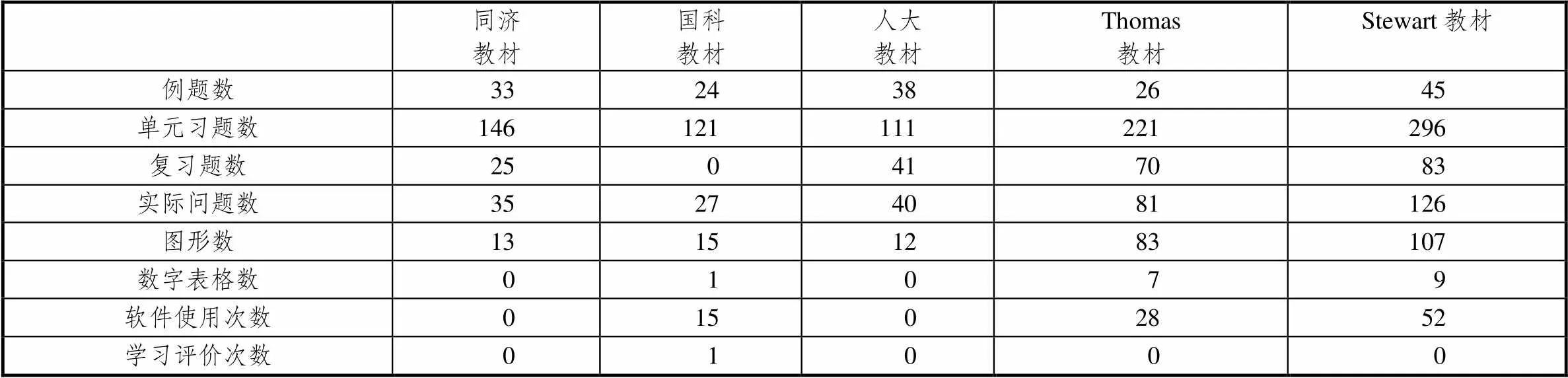
表3 中美教材中其它构成要素的比较

注：表中数据不包括选学内容；Thomas教材不包含二阶微分方程部分．

（1）例题和习题数量的比较．从表3可以看出，中美教材在例题数量上差异不大，但在习题数量上却存在巨大差异．在Thomas教材不含二阶微分方程的情况下，习题总量的平均数，美国教材就达335个，而中国教材仅为148个，只占美国教材的44%．另一方面，教材所含实际问题数，中国平均34个，美国平均103个，是中国的3倍多．由此看出，美国教材习题数量大，且解决实际问题的内容也十分丰富．

（2）数学表征方式的比较．数学表征是影响数学学习的重要因素[30]．然而，从数学表征方式上看，中美教材的差异却十分巨大．教材所含图形的平均数，中国约13个，美国为95个，超过了中国的7倍；数字表格数，中国3套教材仅有1个，美国教材平均8个，远超中国教材．由此看出，美国教材十分重视文字、符号、图形、数字四元表征并举，即使是中国教材只要求解方程的题，美国教材也要求学生用软件作出解函数的图象．中国教材多数情况下仅采用文字和符号两种表征方式．因此，中国教材中的图形和数表明显偏少，需适度增加．

（3）数学软件使用情况的比较．计算和作图软件的使用，中国仅国科教材有15处，美国教材则很普遍，其中的Stewart 教材就多达52处，超过国科教材的3倍．由此可见，中国将软件的操作使用编入教材的很少，将其作为教学和考试内容的就更少了．Stewart教材的作者James Stewart教授认为：“技术非常好，我们已经看到技术是怎样让学生感兴趣，让他们更积极主动地学习．但我们可能滥用技术或者误用技术，或者为了技术而技术．”[21]因此，中国教材需要补充、完善和丰富数学软件操作使用的内容，而美国教材则要防止技术的泛用、滥用和误用．

（4）学习评价测试题的设置情况．总体而言，在学习评价方面，中美的纸质教材都重视不够．这5套教材中，仅国科教材有1套全章的总结性评价检测题．众所周知，教材中的评价内容是供学生学习时自我检测和帮助学生学习的工具，而且检测评价的分数被学生视为是对学习的肯定和褒奖，这对学生的学习动机具有即时的激励作用．因此，要把对学习的评价作为教材设计的一个重要组成部分，即要把教材中评价内容的设计与知识内容的设计放在同等重要的位置上[31]．此外，按照布卢姆关于评价的一般理论，一个完整的评价应该包括课程实施前的诊断性评价，课程实施中的形成性评价和课程实施结束后的总结性评价[32]．因此，仅就这一章而言，至少需要设计2套检测题，一套是章前的诊断性检测题，另一套是章末的总结性检测题（对于整个学期而言，它也是过程性评价）．当然，最好在一阶微分方程内容后，还设计1套过程性评价的检测题．

4 启示与建议

4.1 启示

编写教材时，对课程的各个知识点，编著者需全面、准确、深入把握其内涵，不容有任何偏差；否则，可能会造成知识陈述，甚至编写指导思想上的偏差．如中国教材的编著者，或许是因为他们对“在解决实际问题中，所列的微分方程几乎都无初等解析解”这一细节的疏忽，从而致使其确信，只要教师们教会学生求解几类典型微分方程的方法，学生基本就能求解典型的微分方程，进而就能解决涉及微分方程的实际问题了．因此，在解决实际问题中真正有用的方法，如方向场、欧拉方法和相平面分析法等，均未被他们编入教材．

并非所有培养和训练学生数学能力的做法都值得肯定．对于微分方程，中国教材十分重视学生解方程能力的培养和训练，美国教材则十分重视列方程解决实际问题能力的培养和训练．然而，前者培养的是偏向于解题和考试的能力，而后者培养的则是偏向于解决实际问题的能力．因此，后者值得肯定，前者不可取．这就像培养士兵的作战能力一样．在信息化时代，如果还在强调骑马、射箭和拼刺刀的能力，而忽视了使用信息技术操控无人机和使用现代化装备的能力，那么这支部队必打败仗．因为被重点培养的能力在现代战场上几乎用不上，而用得上的能力却没有得到培养．所以，不能说培养和提高了学生的某项数学能力就是好的，而是要看这个能力是否值得培养，而且还要看是否因此而耽误了更重要能力的培养和提高．

练习题除了具有练习、巩固、提高等显性功能外，还有许多隐性功能．例如，美国教材就将被中国教材编入正文和例题的部分内容编入了习题，从而给练习题赋予了陈述新知识和为解决新问题而举例的功能；又如，美国教材将数学建模的思想方法系统地融入到练习题中，这就给练习题赋予了渗透和培养数学思想方法的功能；再如，在不增加教学课时的前提下，Stewart教材之所以能全面、完整地介绍种群增长模型的庞大体系，就在于它把种群增长的大多数问题纳入了练习题之中，这就赋予了练习题突破难点的功能等．

4.2 建议

（1）增加．增加求解“无初等解析解的微分方程”所需的知识，它们是方向场、欧拉方法、正交轨线、自治方程（组）的解和解曲线的分析方法；增加一些重要而典型的微分方程模型和实例，它们是追迹问题、谣言（信息、疾病等）传播问题、种群的有限增长问题、捕食者—猎物问题、两个种群的竟猎问题；增加使用技术手段进行作图、数值计算、模型分析、参数讨论、图形模拟等内容；习题中适度增加一些探索、讨论型问题，以渗透数学建模的思想方法；适当增加数表和直观图的数量．此外，为更好地帮助学生自学，还可设计2～3套学习评价的检测题．

（2）删减．删去过于形式化和符号化的内容，它们是高阶微分方程的有关概念和表达式、常系数线性高阶微分方程的求解等；减少一些物理和几何应用问题；考虑到知识难度、课时限制和不同专业的需求差异等因素，还可将整个二阶微分方程标注为选学内容．

（3）调整．考虑到与线性代数课程相呼应，可将整个微分方程一章回调至第六版以前的位置[33]（下册级数一章之后），待学生学完线性代数后，再讲函数的线性相关性和非齐次方程解的结构，以节省教学时间[6]，这样也不必将微分方程的幂级数解法编入级数一章，而且整个微积分教材的编排还符合“一元微积分—多元微积分—微积分的应用”这个大的板块结构．此外，也可将相对次要的几个知识点从正文转移到练习题中，它们是齐次方程、伯努利方程、可降阶的高阶微分方程；还可将解一阶线性非齐次方程的常数变易法替换为积分因子法．

5 结语

随着信息化、网络化、移动学习的智能技术的发展，教材电子化[3-4]和教材学材化[34]趋势正在加快．这给教材的编写提出了新的挑战．此外，各国都普遍存在学生提出问题的能力严重不足的问题．因此，有学者指出，数学教材应增加数学问题提出活动的比例与类型[35]．但如何在教材中设计数学问题提出活动，以有效培养和提高学生提出问题的意识和能力，则是一个待解的重大课题．再者，一直以来，中国在培养学生使用技术手段进行作图、计算、分析、探索的能力方面，与国外相比，差距巨大．如何通过教材编写、课堂教学和学习评价来扭转这一局面，这是中国数学教育界面临的一项迫切任务．

总之，教材的编写是一件十分复杂而艰巨的工作．编写一部优秀教材，不仅需要坚实的教育学和心理学的理论支撑，而且更需要编著者有丰富的教学实践经验和对课程内容的深入研究．正如文[36]所说，与写文章和写书相比，一套好的教材最难写，因为它是一个群体（包括数学家、教育学家、心理学家、优秀教师）的长期研究、实验、升华的结晶，它将影响到数以万计学生的终身发展．因此，一部优秀教材不是谁都能写成，更不是随便就能写成的．

[1] 范良火，吴立建．国际数学教材研究和发展趋势述评和分析——从首届国际数学教材研究和发展会议及其大会报告说起[J]．数学教育学报，2015，24（3）：1-5．

[2] 綦春霞，曹辰，付钰．第三届国际数学教材研究与发展会议综述[J]．数学教育学报，2020，29（2）：89-93．

[3] 朱雁，倪明，孔令志，等．数字时代中的数学教材研究与开发及使用——第三届国际数学教材研究和发展会议综述[J]．数学教育学报，2020，29（2）：94-99．

[4] 李娜，范良火．电子数学教材的国际发展趋势——基于第三届国际数学教材研究与发展会议的分析和展望[J]．比较教育学报，2020（6）：145-155．

[5] 张国杰，苏帆，何兴纲．关于数学分析教学改革的综述与思考[J]．数学教育学报，1995，4（2）：47-52．

[6] 张肇炽，叶正麟．“代数与几何”课程及教材的若干设想与初步实践[J]．数学教育学报，1999，8（3）：90-94．

[7] 王彩芬，曹荣荣，张丽，等．中美微积分教材内容建构比较与启示——以“微分”为例[J]．数学教育学报，2021，30（4）：63-67．

[8] 胡静波．中美经典微积分教材比较研究[J]．湖北科技学院学报，2015，35（6）：13-15．

[9] 薛有才，胡月，叶赛英．中美典型微积分教材比较分析与思考[J]．科技与出版，2006（2）：73-74．

[10] 叶赛英，胡月．国内外两本微积分教材的比较与启示[J]．大学数学，2007，23（1）：187-190．

[11] 郭镜明，朱晓平，应明．交流互补融合提高——中美微积分教材内容的比较[J]．高等数学研究，2006，19（1）：6-10．

[12] 吴志坚，肖滢，吴兴玲．中美微积分教材比较研究[J]．高等数学研究，2010，23（3）：43-47．

[13] 田仕芹，王玉文．中美高等数学教材内容的比较研究——以美国宾夕法尼亚九版和中国同济七版为例[J]．数学教育学报，2017，26（2）：75-79．

[14] 平艳茹．中美大学微积分教材之比较[J]．科技资讯，2012（8）：197-198．

[15] 郭镜明，应明，朱晓平．美国微积分教材中的习题配置特色[J]．大学数学，2005，21（2）：13-16．

[16] 高雪芬，汪晓勤．M·克莱因的HPM思想——以《微积分》为例[J]．数学教育学报，2012，21（4）：24-27．

[17] 王海青，汤志娜．大学先修课程背景下美国AP微积分教材的编写特色与启示[J]．数学教育学报，2018，27（2）：74-77．

[18] 同济大学数学科学学院．高等数学（上册）[M]．8版．北京：高等教育出版社，2023：289-354．

[19] 朱建民，李建平．高等数学（上册）[M]．2版．北京：高等教育出版社，2015：312-349．

[20] 吴赣昌．高等数学（理工类，上册）[M]．3版．北京：中国人民大学出版社，2008：281-339．

[21] Stewart J，白峰杉．畅销背后的奥秘——访《微积分》教材作者James Stewart [J]．中国大学教学，2003（10）：36-37．

[22] Stewart J. Calculus early transcendentals [M]. 6th ed. Belmont: Thomson Brooks / Cole, 2008: 340-350, 566-619, 1 110-1 138.

[23] GEORGE B, THOMAS, JOEL H, et al. Thomas’ calculus [M]. 14th ed. Boston: Pearson Education, 2018: 231-247, 397-406, 526-562.

[24] 陈重穆，宋乃庆．淡化形式，注重实质——兼论《九年义务教育全日制初级中学数学教学大纲》[J]．数学教育学报，1993，2（2）：4-9．

[25] 宋乃庆，陈重穆．再谈“淡化形式，注重实质”[J]．数学教育学报，1996，5（2）：15-18．

[26] 同济大学数学科学学院．高等数学（下册）[M]．8版．北京：高等教育出版社，2023：282-284．

[27] 朱建民，李建平．高等数学（下册）[M]．2版．北京：高等教育出版社，2015：254-255．

[28] 黄健，徐斌艳．国际视野下数学建模教与学研究的发展趋势——基于第14 届国际数学教育大会的分析[J]．数学教育学报，2023，32（1）：93-98．

[29] 李保臻，陈国益．高中数学教科书中数学建模问题情境的比较研究[J]．数学教育学报，2022，31（3）：6-14．

[30] 沈阳，张晋宇，鲍建生．表征在数学教育中的研究现状[J]．数学教育学报，2022，31（2）：82-89．

[31] 霍雨佳，黄翔．发掘数学教材的评价功能——对美国加州小学数学教材的分析与启示[J]．数学教育学报，2011，20（3）：76-79．

[32] 张华．课程与教学论[M]．上海：上海教育出版社，2000：265-270．

[33] 同济大学数学系．高等数学（下册）[M]．5版．北京：高等教育出版社，2002：259-328．

[34] 曹一鸣，吴立宝．初中数学教材难易程度的国际比较研究[J]．数学教育学报，2015，24（4）：3-7．

[35] 许天来，蔡金法．美国数学课程中的“问题提出”——期望与挑战[J]．数学教育学报，2019，28（2）：18-23．

[36] 李善良．论中小学数学教材编写的基本原则[J]．数学教育学报，2007，16（1）：70-73．

Comparative Study of Differential Equations in Calculus Textbooks of Chinese and American Universities

PAN Jian-hui1, HU Xue-gang2, ZHU Wei1, DENG Zhi-ying1, CHEN Ji-lin3

(1. School of Science, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;2. Dean’s Office, Chongqing University of Posts and Telecommunications, Chongqing 400065, China;3. Tianxingqiao High School of Chongqing, Chongqing 400038, China)

A comparative study of the contents of differential equations in 5 sets of calculus textbooks for Chinese and American universities found that there are many significantly different aspects in the two types of textbooks, such as the content layout, the number of exercises, mathematical representation methods, the use of mathematical software, the degree of emphasis on mathematical modeling, the processing of secondary or higher required content, and the number and types of real world problems solved by the differential equation models. In addition, American textbooks have many practices worth learning from in terms of ideological and method guidance on mathematical modeling and breakthroughs in difficult mathematical modeling problems. However, a major defect in Chinese textbooks is that most of the knowledge required to solve the “differential equations without primary analytical solutions” is not included in the textbooks. Then, three inspirations are obtained: first, the textbook writers’ misunderstanding of knowledge points may lead to deviations in the guiding ideology; second, the cultivation and the training of mathematical abilities are not always beneficial; third, the exercises have many invisible functions that need to be developed and utilized. Finally, three revision suggestions are put forward for Tongji Textbook: add direction field, Euler method and other important content; delete overly formal content such as higher-order differential equations; and adjust the arrangement position of power series solutions to differential equations and other contents.

university textbooks; calculus; differential equation; comparative study; mathematical modeling

G642

A

1004–9894（2024）01–0064–07

潘建辉，胡学刚，朱伟，等．中美大学微积分教材之微分方程内容的比较研究[J]．数学教育学报，2024，33（1）：64-70．

2023–08–10

重庆市高等教育教学改革研究重大项目——政产学研用深度融合的协同育人模式研究与实践（221018）；重庆市研究生教育教学改革重点项目——新工科背景下“五维一体”研究生数学课程思政体系的综合研究与实践（YJG212022）；重庆市高等教育教学改革研究项目——大学数学“前移式问题解决”教学模式的实验研究（213161）；重庆市研究生课程思政示范课程项目——决策理论与决策支持（YKCSZ23121）；重庆邮电大学金课建设基金项目——《实变函数》线下金课（XJKXX20201-15）

潘建辉（1965—），男，四川武胜人，副教授，硕士，主要从事数学课程与教学论研究．

[责任编校：陈隽、陈汉君]