陶瓷透水路面砖渗透系数与孔隙特征的定量关系模型

王仪良， 谭建平， 李薇， 任文渊，*， 袁克阔

（1.西北农林科技大学 水利与建筑工程学院，陕西 杨凌 712100；2.西京学院 土木工程学院，陕西 西安 710123）

随着海绵城市战略的提出，透水路面砖受到越来越多的关注，已被广泛应用于人行道、公园及停车场等区域.其优良的抗滑和降噪特性为人们出行提供了安全与舒适保障条件.为此国内外学者对透水路面材料的性能展开了大量研究.

崔新壮等［1］和刘冠志等［2］分别研究了暴雨作用下淤塞以及骨料粒径的改变对于透水路面材料孔隙结构的影响.透水混凝土渗透系数的影响因素也受到了众多学者关注［3‑6］.国外众多学者对孔隙特征参数与渗透系数的关系进行了大量研究［7‑8］，提出了基于孔隙体积和孔隙半径预测渗透系数的经验公式，获得了较好效果.然而，这些研究主要基于孔隙半径和孔隙率等基本参数，而未涉及孔隙形状及分布等参数与渗透特性之间的关系.

本文拟利用X射线计算机断层成像（X-ray computed tomography，XCT）与图像三维重构技术，获得孔隙三维模型，提取孔隙特征参数.基于沿程水头损失及局部水头损失影响机制，对孔隙特征参数进行相关性分析.然后，结合量纲分析法建立渗透系数与孔隙特征参数之间的定量关系模型，并基于孔隙模型的渗流数值模拟结果进行验证，希望为透水路面材料的应用及优化选用提供理论参考.

1 试验

1.1 陶瓷透水路面砖

以陶瓷透水路面砖为研究对象，规格为200 mm（长）×100 mm（宽）×55 mm（高）的长方体，抗压强度为40 MPa，抗折强度大于6 MPa，透水系数大于0.2 mm/s，耐磨性能满足磨坑长度小于35 mm，抗滑性能满足防滑指标（BPN值）大于60，其他性能指标符合GB/T 25993—2010《透水路面砖和透水路面板》要求.透水砖烧制流程为：在透水砖高度方向进行两次布料和一次烧结成型，上层为细集料，下层为粗集料，从而形成上层小而下层大的孔隙结构，其中，粗细集料均为废旧陶瓷经过高温煅烧之后的陶瓷颗粒.当淤堵物随雨水从表面进入透水砖内部时，结构的反滤特性可满足透水砖透水功能的长期有效性.

试样制样方法：为获得较高精度孔隙结构信息，对整砖试件进行钻芯取样，得到保留原整砖试样高度方向结构分布的圆柱芯样，其直径为50 mm，高度为55 mm，如图1所示.

图1 透水砖圆柱芯样（截取自实际试样）Fig.1 Cylindrical core sample of pervious brick（actual specimens intercepted）

1.2 XCT扫描

XCT技术具有分辨率高、无损测试和三维可视化等优点，可用来无损捕捉混凝土试件中的真实空间分布和形态特征［9‑10］，还可为骨料与孔隙三维形态表征以及更接近真实形态随机骨料模型的生成提供参考和依据［11］，在材料孔隙结构研究中已经得到了广泛应用［12‑16］.

设备使用Multiscale-Voxel 450 kV工业XCT扫描仪（CD-300BX），扫描圆柱芯样获得图像模型大小为1 200 像素×1 200 像素，共采集到1 300幅图像，XCT扫描空间分辨率为43.63 μm.

2 孔隙特征参数

透水路面材料中的孔隙主要分为封闭孔隙、半封闭孔隙和连通孔隙3类.其中连通孔隙又称为有效孔隙，对透水路面材料渗透系数的影响最大.另外两类孔隙对于透水路面材料的渗透系数影响较小.故本文主要讨论陶瓷透水路面砖中有效孔隙及其特征参数，如无特别说明，下文中孔隙特征参数均指有效孔隙特征参数.

2.1 孔隙三维模型建立

将扫描得到的图像进行三维重构，并对其进行滤波处理，得到圆柱芯样的灰度切片图像.将灰度图像导入Avizo软件进行阈值分割，将孔隙相与集料相分离.最终得到透水砖圆柱芯样的三维孔隙模型，如图2所示.

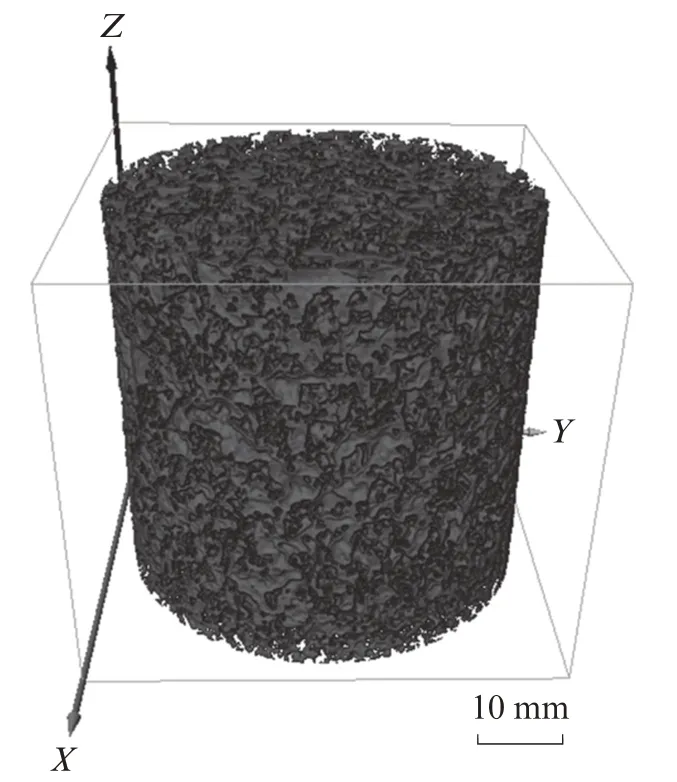
图2 透水砖圆柱芯样的三维孔隙模型Fig.2 3D pore model of pervious brick cylindrical core sample

基于三维孔隙模型，选取能够代表孔隙模型结构特征的表征单元体（representative volume element，RVE）代替原模型.表征单元体是多孔介质渗流中重要的概念，是宏观尺度上保持介质性质基本稳定的最小单元［17］.以结构有效孔隙率维持稳定为选取原则确定RVE尺寸.考虑到圆柱芯样原模型是分层建立的，且下层高度较高，故确定下层孔隙模型RVE尺寸的具体步骤如下：随机在三维孔隙模型中选取4个不同形心的RVE；逐步增加这4个RVE的尺寸，并计算其有效孔隙率的变化；当RVE的有效孔隙率不随尺寸大小变化时，即为目标RVE尺寸.分析结果见图3，其中软件计算得到的圆柱芯样整体结构有效孔隙率为15.23%.

图3 RVE尺寸与孔隙率变化曲线Fig.3 RVE size and porosity variation curve

从图3可以看出，当选取的RVE尺寸逐步增加到13.1 mm时，其有效孔隙率基本维持稳定.考虑设备算力，应尽可能缩小模型以减少计算量，故最终取下层孔隙结构模型的RVE尺寸为13.1 mm×13.1 mm×13.1 mm.同时，鉴于上层孔隙层高度较小，因此直接选取上层孔隙结构模型厚度6.5 mm作为上层RVE高度尺寸，故上下层贯通后RVE尺寸为13.1 mm×13.1 mm×19.6 mm.在圆柱芯样孔隙结构模型中随机选取24个RVE，考虑到其与圆柱芯样边界的位置关系，RVE形心位置如图4所示.

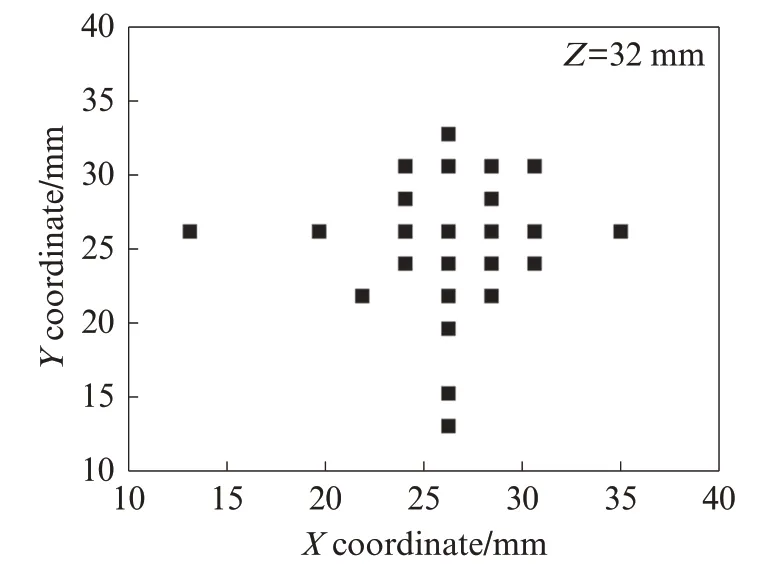
图4 RVE形心位置Fig.4 RVE shape center locations

2.2 孔隙特征参数

2.2.1 孔隙特征参数的选取

达西定律中渗透系数的计算式见式（1）.

式中：K为渗透系数，mm/s；v为渗流流速，mm/s；i为渗流水力坡降.

分析式（1）中流速v与水力坡降i的影响因素，以选取合适的孔隙特征参数.在给定进出口压力和渗流试样长度的前提下，其水力坡降i是一定的，而流速v的大小受到沿程水头损失与局部水头损失的影响.其中沿程水头损失为渗流过程中流体与孔隙内壁间的摩擦力于渗流路径长度内所做的负功，受到孔隙迂曲度（直接控制渗流路径长度）及孔隙半径（影响渗流速度梯度大小，从而间接影响黏滞力大小）［18］的影响；局部水头损失主要发生在孔隙截面突变处，受到孔隙喉道及截面突变程度（由孔隙形状表征）的影响.

将圆柱芯样孔隙模型作分割并剔除非有效孔隙后，对所得24个RVE孔隙模型进行特征参数的全面获取与筛选.综合分析比较有效孔隙率、有效孔隙比表面积、有效孔隙迂曲度、有效孔隙半径均值、有效孔隙三维分形维数、有效孔隙平均孔喉比、有效孔隙平均配位数、有效孔隙团簇离心率、有效孔隙等效喉道半径、有效孔隙等效喉道长度、有效孔隙费雷特直径和欧拉示性数等孔隙特征参数，根据“能够独立控制”、“对渗透性能影响大”和“相近代替取更优”原则，将以下3类参数筛去：（1）描述孔隙综合信息的孔隙三维分形维数（难以独立控制）；（2）经数据分析对渗透系数影响较小的有效孔隙率、有效孔隙平均配位数、孔隙费雷特直径和欧拉示性数；（3）能够由更优参数替代的有效孔隙平均孔喉比（由喉道长度、喉道半径代替）和团簇离心率（由比表面积代替）.利用SPSS软件得到剩余各孔隙特征参数间的线性相关程度，结果见表1，表中数字为皮尔逊相关性（R）.

表1 各孔隙特征参数间的线性相关程度Table 1 Degree of linear correlation between pore characteristic parameters

由表1可见，孔隙半径均值与孔隙等效喉道长度、喉道半径存在较为显著的线性相关关系，这是因为喉道作为孔隙的一部分，必然会对孔隙半径均值产生影响.孔隙喉道作为孔隙渗流过程的关键制约段（类比于“木桶效应”中的“短板”），其重要性不言而喻.想要将孔隙结构特征进行完整表征，必然需要孔隙喉道的参与，且孔隙喉道作为孔隙中形状较为规则的部分，由沿程方向的喉道长度及横截面方向的喉道半径来表征.孔隙半径均值作为孔隙横截面方向信息的综合，还受到除喉道之外的其他因素影响，其在极大程度上影响渗流流速梯度，进而影响黏滞力大小，最终影响沿程水头损失，故必须选取其作为孔隙特征参数.

基于上述分析，确定了影响沿程水头损失的有效孔隙迂曲度、有效孔隙半径均值，以及影响局部水头损失的有效孔隙比表面积（表征孔隙形状）、有效孔隙等效喉道半径与有效孔隙等效喉道长度作为本文透水路面砖孔隙特征参数.

2.2.2 孔隙特征参数的获取

有效孔隙迂曲度τ表征整个渗流路径沿程方向的信息，其计算式见式（2）.

式中：L为渗流试样长度，mm；Le为实际渗流路径长度，mm.

Le的计算方法为：将孔隙结构模型沿Z轴（高度方向）切割为多个微元平面，获取每个微元平面上的有效孔隙形心点，连接各形心点，计算各连接微元段长度的总和，即Le.

有效孔隙比表面积S表征有效孔隙形状信息，其计算式为：

式中：Sp为有效孔隙表面积，μm2；Vp为有效孔隙体积，μm3.

有效孔隙等效喉道半径req表征渗流路径中有效孔隙喉道的横截面信息，其计算使用最大内切球算法，即有效孔隙内最窄处等效体积最大球的半径.

有效孔隙等效喉道长度leq表征有效孔隙喉道的沿程方向信息.leq为喉道两端所连接2个有效孔隙等效体积球体心之间距离减去2个等效体积球半径之后的长度.

有效孔隙半径均值r指有效孔隙以渗径为圆柱母线，以体积不变为原则等效为圆柱型孔隙的半径.

通过计算共获得24组数据，计算孔隙特征参数与其均值的比值，得到如图5所示的孔隙特征参数波动曲线.由图5可知，陶瓷透水砖内有效孔隙迂曲度、有效孔隙半径均值、有效孔隙等效喉道半径和有效孔隙等效喉道长度围绕各自均值在±10%范围内波动，有效孔隙比表面积则基本稳定，无明显变化.

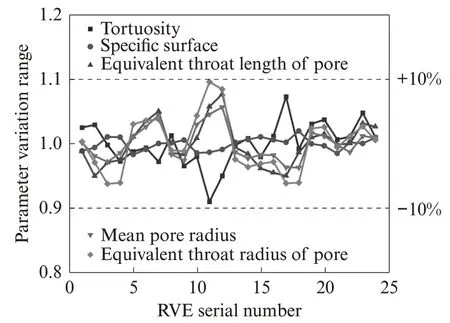
图5 孔隙特征参数波动曲线Fig.5 Variation range curves of pore characteristic parameters

2.3 宏观有效孔隙率试验

利用质量法对经XCT扫描的透水砖圆柱芯样进行有效孔隙率测定，并与计算值对比，以验证软件仿真的可信度.试验步骤如下：

（1）测算无水干燥条件下透水砖圆柱芯样的直径d、高度h和质量md，精度分别为0.02 mm和0.01 g；

（2）将透水砖圆柱芯样置入饱和缸内，对饱和缸进行抽真空处理之后静置24 h，使透水砖圆柱芯样充分饱水；

（3）利用保鲜膜在饱和缸水面下将圆柱芯样紧密贴合包裹完全，之后小心取出，测量其质量m0；

（4）将含水保鲜膜快速小心取下，测定其质量mp；

（5）按下式计算实测透水砖圆柱芯样有效孔隙率φ.

式中：ρw为水的密度.

试验共测量7次，剔除最大值与最小值后，取其均值作为最终的实测透水砖圆柱芯样有效孔隙率，为21.93%，其与仿真计算得到的有效孔隙率15.23%相差较大，主要原因有以下几点：

（1）有部分微孔隙的尺寸小于XCT扫描分辨率，在图像处理时被包含在圆柱芯样集料相中，无法被划分为孔隙相，导致软件计算值较真实值偏低.

（2）存在回孔效应［19］.因为XCT扫描无法精准识别深度，故一部分孔隙在XCT扫描时会被该扫描面下层集料“穿透”，造成一部分孔隙被误判成集料，导致软件计算的有效孔隙率较真实值偏低.

（3）宏观有效孔隙率试验中，抽真空会导致半封闭孔隙被水充满，导致实测有效孔隙率较真实值偏大.

综上，有效孔隙率误差主要由XCT扫描及有效孔隙率实测试验的系统误差导致，因此单纯由软件本身引起的有效孔隙率计算误差可以忽略不计，即认为软件的计算结果是可靠的.

3 理论公式

3.1 理论公式设计

根据选定的对孔隙渗透性能影响较大的几个参数（τ、r、S、req、leq）的物理意义，建立绝对渗透率k与孔隙特征参数之间的关系，见式（5）.

绝对渗透率k与渗透系数K存在式（6）所示关系.

式中：γ为渗流流体的容重，N/m3；μ为渗流流体的动力黏滞系数，Pa·s.

结合式（5）、（6），得到拟定的渗透系数与孔隙特征参数之间的关系，如式（7）所示.其中，式（7）中各孔隙特征参数应该严格以μm或μm-1为单位.由式（7）中各孔隙特征参数的幂次大小可知：孔隙迂曲度τ及孔隙半径均值r对于透水材料渗透系数影响最大，其余参数影响次之.

3.2 试验验证

在Avizo软件中，对选取的24个RVE孔隙模型使用Axis Connectivity命令获得其连通孔隙模型，该命令可以将孔隙模型中不与Z轴上下表面连通的孔隙进行剔除，获得的连通孔隙模型见图6.而后对其进行渗流模拟，在给定的入口压力、出口压力、渗流液体动力黏滞系数和主要渗流方向等参数条件下，对连通孔隙模型进行渗流模拟，渗流流速云图见图7.同时，计算得到各RVE孔隙模型的渗透系数仿真值，见表2.

表2 RVE孔隙模型渗透系数仿真值Table 2 Simulated permeability coefficient of RVE connectivity pore model

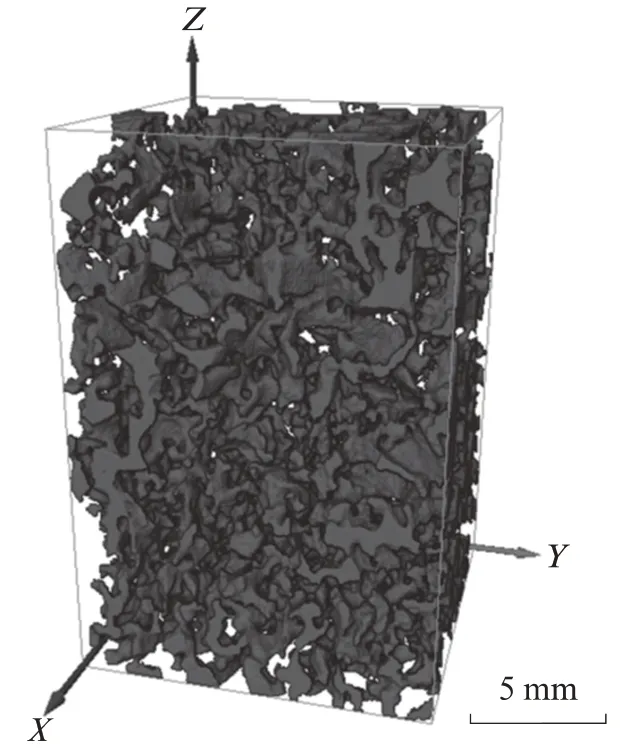
图6 RVE连通孔隙模型Fig.6 RVE connectivity pore model

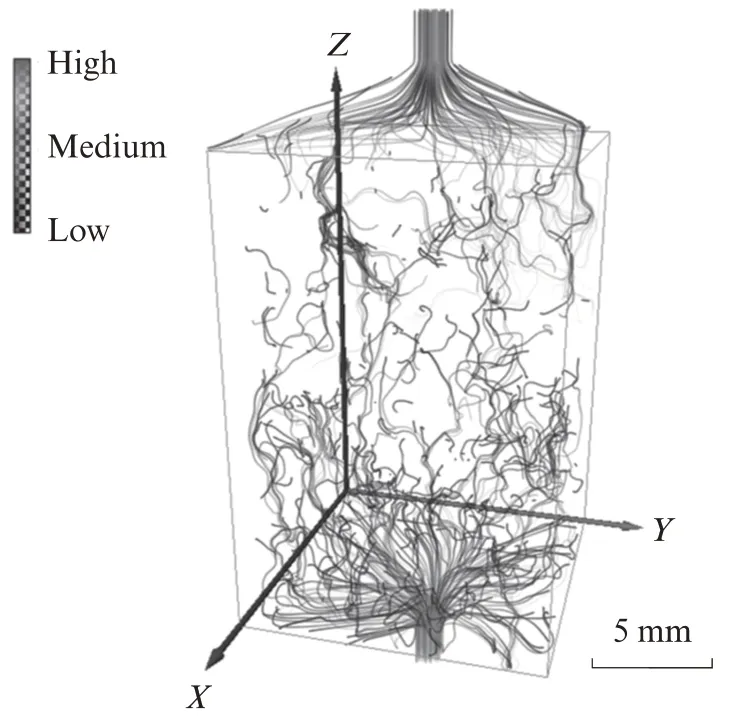
图7 渗流模拟流速云图Fig.7 Simulated flow velocity clouds for seepage

将由式（7）得到的渗透系数公式计算值Kcv与数值软件得到的渗透系数仿真值Ksv进行对比，如图8所示，发现两者的线性相关关系较好.

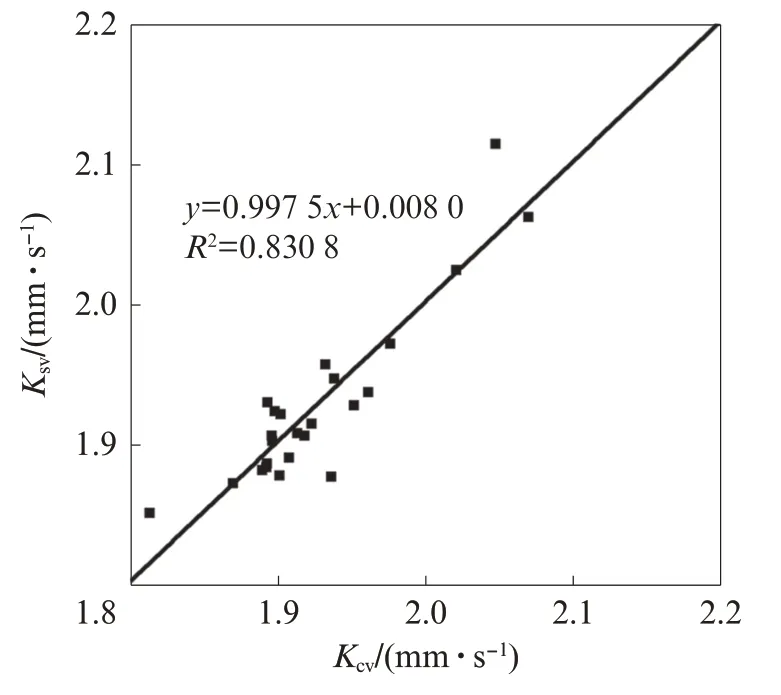
图8 计算值与仿真值对比Fig.8 Comparison of calculated values with simulation values

利用SPSS软件对渗透系数计算值与仿真值进行回归分析，得到方差分析结果和回归系数，分别见表3和表4.其中：F为F检验值；B为标准化前每个自变量在回归方程中的系数；Beta为标准化后自变量在回归方程中的系数；t为t检验值.

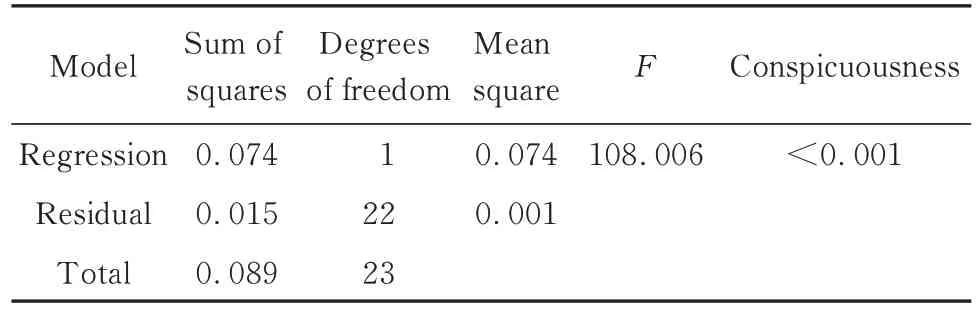
表3 渗透系数方差分析结果Table 3 Analysis of variance for permeability coefficient

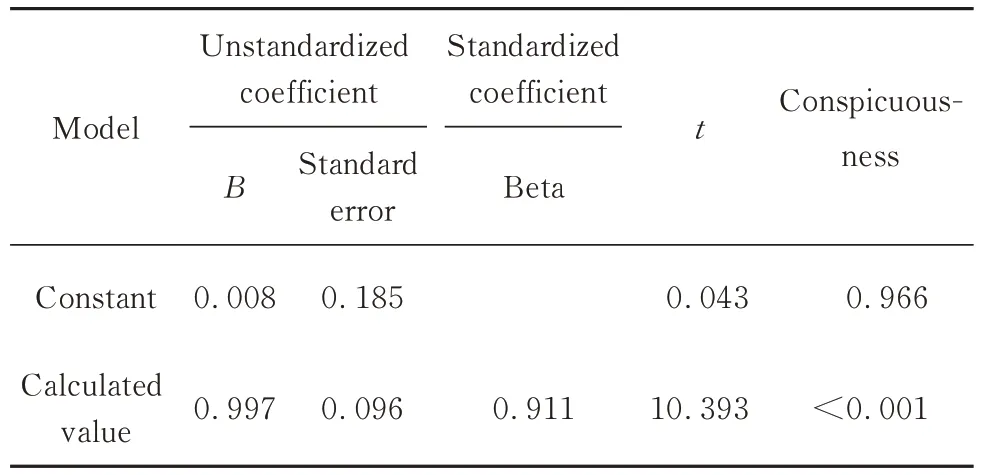
表4 回归系数Table 4 Regression coefficients

从表3和表4可以看出，其F检验及t检验的显著性均小于0.001，远小于0.05，说明所建线性回归模型具有较为显著的可靠性.因此，可以认为式（7）模型是合理可靠的.

经计算，渗透系数计算值均值与渗透系数仿真值均值的相对误差为0.16%，远小于5%，说明式（7）能够在较大程度上反映孔隙结构特征对于透水路面材料渗透性能的影响规律.

4 结论

（1）建立了陶瓷透水路面砖渗透系数与孔隙特征参数的定量关系模型，经过检验确定了该模型的可靠性与合理性.

（2）陶瓷透水路面砖渗透系数受有效孔隙迂曲度和有效孔隙半径均值的影响最大，受有效孔隙比表面积、有效孔隙等效喉道半径及有效孔隙等效喉道长度的影响次之.