多喷嘴对置式气化炉耐火衬里温度及应力场的有限元分析
2021-03-09苏暐光史雨晨宋旭东王文鑫王焦飞白永辉姚敏于广锁
苏暐光史雨晨宋旭东王文鑫王焦飞白永辉姚 敏于广锁
(1.宁夏大学 省部共建煤炭高效利用与绿色化工国家重点实验室,宁夏 银川 750021; 2.宁夏大学 化学化工学院,宁夏 银川 750021; 3.国家能源集团宁夏煤业有限责任公司,宁夏 银川 750001;4.华东理工大学 洁净煤技术研究所,上海 200237)
在我国,煤炭在相当长时间内依然是最重要的能源资源[1-3]。由华东理工大学和兖矿集团共同开发的OMB 水煤浆气化技术是我国拥有自主知识产权的大型煤气化技术[4],该技术是世界气化市场上的领先技术之一[5]。目前已在国内外建立57 个项目、158台气化炉,累积总原料处理能力大于20 万t 煤/d,单炉最大规模4 000 t/d,OMB 气化炉在大型气化应用中具有极大优势[6]。耐火衬里是该气化炉最重要的组成之一,主要起到隔绝高温、蓄热、流场约束以及抗熔渣的作用,而且直接影响气化炉的运行周期和稳定性[7]。气化炉内高温环境[8-9]会导致耐火衬里产生热应力,从而出现裂纹,炉内的渣和强还原性气氛会通过裂纹加速耐火衬里的损坏,影响气化炉的正常使用[10-11]。气化炉运行时,只能通过热电偶检测炉内壁的温度,耐火衬里内部的温度分布很难得知,用实验方法研究热应力更是困难重重。有限元法已经广泛应用于温度场的数值模拟研究。张官正等[12]采用ANSYS 软件研究了矿热炉炉衬中的温度场分布,结果表明升高炉内温度和增大对流换热系数都会使炉壁温度升高。吴新华等[13]运用有限元方法研究了烘烤和盛钢工况下的钢包温度场分布情况,模拟结果与红外测温法测得的温度分布基本一致。李公法等[14]研究了材料导热系数对新型钢包温度场的影响,结果表明钢壳温度随导热系数减小而降低。
此外,利用有限元法进行耐火衬里热应力研究大多应用于冶金行业。张德臣等[15]利用有限元法对高炉耐火砖的热应力和变形进行平面应力分析,得到了距热面1/3 处出现应力峰值且热面砖热面膨胀较大。郭志强等[16]通过有限元法计算了转炉炉壳受到热载荷时的热膨胀应力和温度差应力的分布情况,认为在总热应力中热膨胀应力所占比例大于温度差应力。LI Gongfa 等[17]运用有限元法研究了二维钢包模型的热膨胀系数、弹性模量及其厚度对钢包温度和应力场的影响,结果表明钢包内部等效应力随衬里导热系数、热膨胀系数、弹性模量的增大而增大,随衬里厚度增大而减小。随后他们[18]研究了含有纳米绝热材料的新型钢包的温度场和应力场。结果表明纳米绝热材料的绝热效果更好,新型钢包的壳体最大温度和应力均小于传统钢包。XUE Wendong 等[19]对COREX-3000 气化炉拱顶进行了数值模拟分析,研究了导热系数与热应力之间的关系。结果表明,当内层衬里和外层衬里的导热系数分别为0.95 和0.50 W/(m·℃)时,沿径向方向拱顶应力的变化率最小。
周俊虎等[20]利用有限元法计算分析了锅炉水冷壁渣层变负荷引起的热应力,得出外渣层(未熔化)的热应力较内部热应力大。陈光等[21]运用有限元法建立了喷嘴模型,研究结果表明随着燃烧器负荷增加,耐火砖热变形增加,外侧空气流速增加,耐火砖热变形减缓。林伟宁等[22-24]运用有限元法对气流床气化炉水冷壁的热应力进行了研究,结果表明液态渣层不存在热应力,固态渣层的热应力随温度升高而增大。
综上所述,目前多喷嘴对置式水煤浆气化炉内耐火衬里的温度场尤其是应力场的相关研究并不多见。当气化炉开车之后,绝大部分时间气化炉都是处于稳定运行状态,因此研究气化炉稳定运行状况下耐火衬里的应力分布规律同样十分重要。笔者针对OMB 气化炉的实际工况,运用有限元软件ANSYS 对正常稳定运行过程中的工业OMB 气化炉耐火衬里蚀损较快的K 砖部位进行分析,通过改变热面砖热端面温度和热面砖厚度,得到温度场、应力、应变及总变形的分布规律。
1 结构模型
OMB 气化炉炉壁主要由耐火衬里和钢壳组成,耐火衬里由热面砖、背衬砖、隔热砖、陶瓷纤维构成。由于热面砖与炉中还原性气氛、煤渣以及高温环境直接接触,因此蚀损较快,且不同位置的热面砖蚀损率不同。K 砖是位于筒体最上部位置的热面砖,具体位置如图1(a)蓝色椭圆区域。筒体部位平均蚀损率为0.076 mm/h,其中K 砖部位蚀损最快[10]。因此,选择K 砖部位的耐火衬里作为研究对象。
工业上OMB 气化炉炉内K 砖部位实物如图1所示,其中图1(a)可以看到K 砖端面是向前突出的斜面,图1(b)为K 砖上方的膨胀缝见蓝色椭圆区域。

图1 OMB 气化炉炉内Fig.1 Physical diagram of OMB gasifier
图2为K 砖部位的结构模型,其中热面砖(即K砖)厚度230 mm,背衬砖厚度200 mm,隔热砖厚度105mm,钢壳厚度86 mm。以炉膛中心为坐标原点,垂直高度为y轴,耐火衬里侧面下底边为x轴建立坐标系。研究对象为气化炉运行时稳态条件下的炉内耐火衬里。由于气化炉炉内的实际工况复杂,因此在数值模拟计算中对实际工况条件进行了部分简化。耐火砖受热膨胀会使预留的膨胀缝被填充,因此假设砖与砖之间接触无间隙,仅考虑各砖之间的热传导。材料物性参数均为各向同性,耐火衬里的导热系数、热膨胀系数恒定,不随温度而变化。忽略重力和炉内压力,仅考虑热应力。
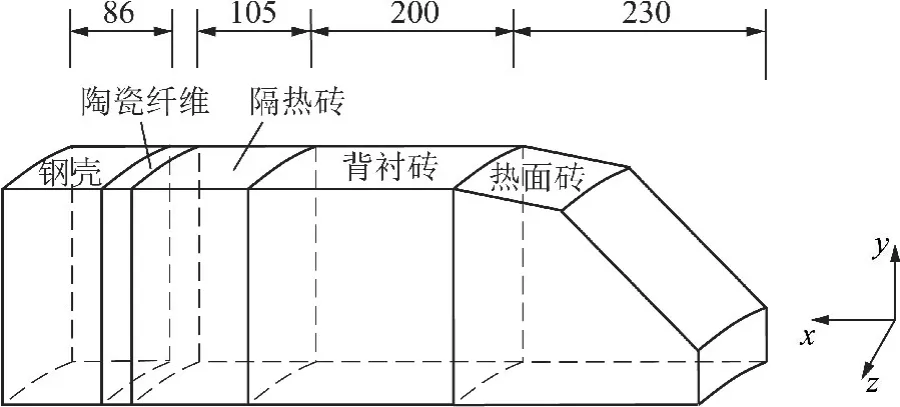
图2 OMB 气化炉K 砖部位的结构模型Fig.2 Structure model of K-brick in OMB gasifier
2 边界条件及材料物性参数
耐火衬里及钢壳的温度场可根据下式无热源、稳态条件下热传导三维微分方程进行计算:
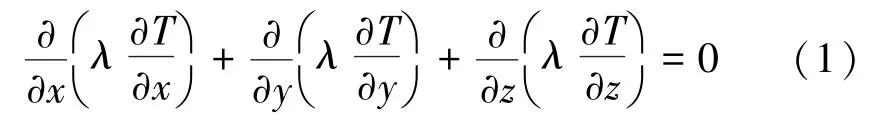
式中,λ为材料导热系数,W/(m·℃);T为温度,℃;x,y和z为空间坐标值,mm。
钢壳与周围环境联合传热的边界方程为

式中,hk为对流-辐射联合换热系数,W/(m2·℃);hc为钢壳与周围环境的自然对流换热系数,W/(m2·℃);hr为辐射换热系数,W/(m2·℃);Tk为钢壳周围环境温度,℃。
对于三维应力场,耐火衬里及钢壳x,y和z三个方向都应满足
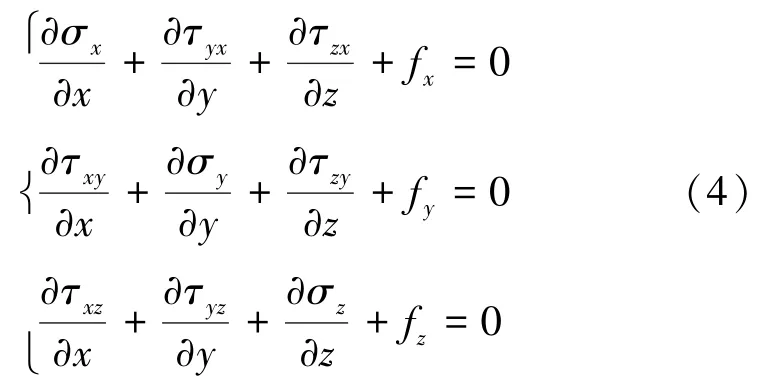
其中,fx,fy和fz分别为耐火衬里及钢壳在x,y和z三个方向的单位体积力。在该模型上施加初始温度以及约束条件,得到方程的惟一解。
将工业气化炉K 砖部位热电偶测得的热面砖端面温度作为传热边界条件,耐火砖之间的传热均视为热传导。钢壳外表面与周围环境的传热方式主要为自然对流和辐射的联合传热,对流-辐射联合传热系数通过经验公式[25]计算为18.38 W/(m2·℃),环境温度为20 ℃。采用热-结构耦合的方法,将温度计算结果作为结构计算的初始条件。对模型下底面施加Y轴方向的位移约束,两侧面施加对称约束,钢壳外表面和热面砖热端面均施加x轴方向的位移约束。本研究重点考察了热面砖热端面温度和热面砖厚度对耐火衬里及钢壳温度分布、等效应力、等效应变和总变形的影响。
耐火衬里和钢壳的材料物性参数见表1,图3为热面砖、背衬砖和隔热砖的弹性模量及泊松比随温度升高的变化情况,测试方法为脉冲激振法。

表1 材料物性参数Table 1 Physical properties of materials

图3 热面砖、背衬砖、隔热砖的弹性模量和泊松比随温度变化曲线Fig.3 Variation of elastil modulus and Poisson’s ratio of hot-face brick,backup brick,heat isolation brick with the increase of temperature
3 结果与讨论
3.1 耐火衬里温度和应力场分析
工业上,OMB 气化炉内温度一般为1 250~1 350 ℃[26],而热面砖温度较炉膛中心温度低,K 砖部位热电偶测得热端面平均温度约为1 300 ℃[27-28],因此热面砖热端面温度设定为1 300 ℃。以图2结构模型尺寸为基础,计算得到耐火衬里和钢壳的温度、等效应力、等效应变以及总变形分布云图。热面砖(K 砖)端面拐角处(距下底面40 mm)到钢壳表面的水平线为Path1,热面砖上部拐角处到下底边垂直距离为Path2,分别从不同角度分析耐火衬里的温度场、应力场、应变和总变形的变化趋势。
图4为耐火衬里及钢壳的温度分布云图,图4(a)为整体耐火衬里及钢壳的温度分布云图,可得热面砖热端面温度为1 300 ℃时,计算得热面砖与背衬砖之间温度为1 131.2 ℃,背衬砖与隔热砖之间温度为929.7 ℃,隔热砖与陶瓷纤维之间温度为441.8 ℃,陶瓷纤维与钢壳之间温度为214.2 ℃,钢壳外表面温度为206.4 ℃。工业数据测得K 砖位置处钢壳外表面温度为200~230 ℃[29],模拟计算结果能够与工业数据较好吻合。图4(b)为Path1 的温度分布线,可清晰看到隔热砖和陶瓷纤维降温幅度较大,这是因为隔热砖和陶瓷纤维导热系数较低,能够阻隔大量热量,可以有效保护气化炉壳体不超温。由于钢壳的导热系数较大,钢壳整体温差仅为8 ℃。图4(c)为Path2 的温度分布线,可得由点1 到点2 方向温度逐渐降低,其中热面砖上部拐角处温度最高。
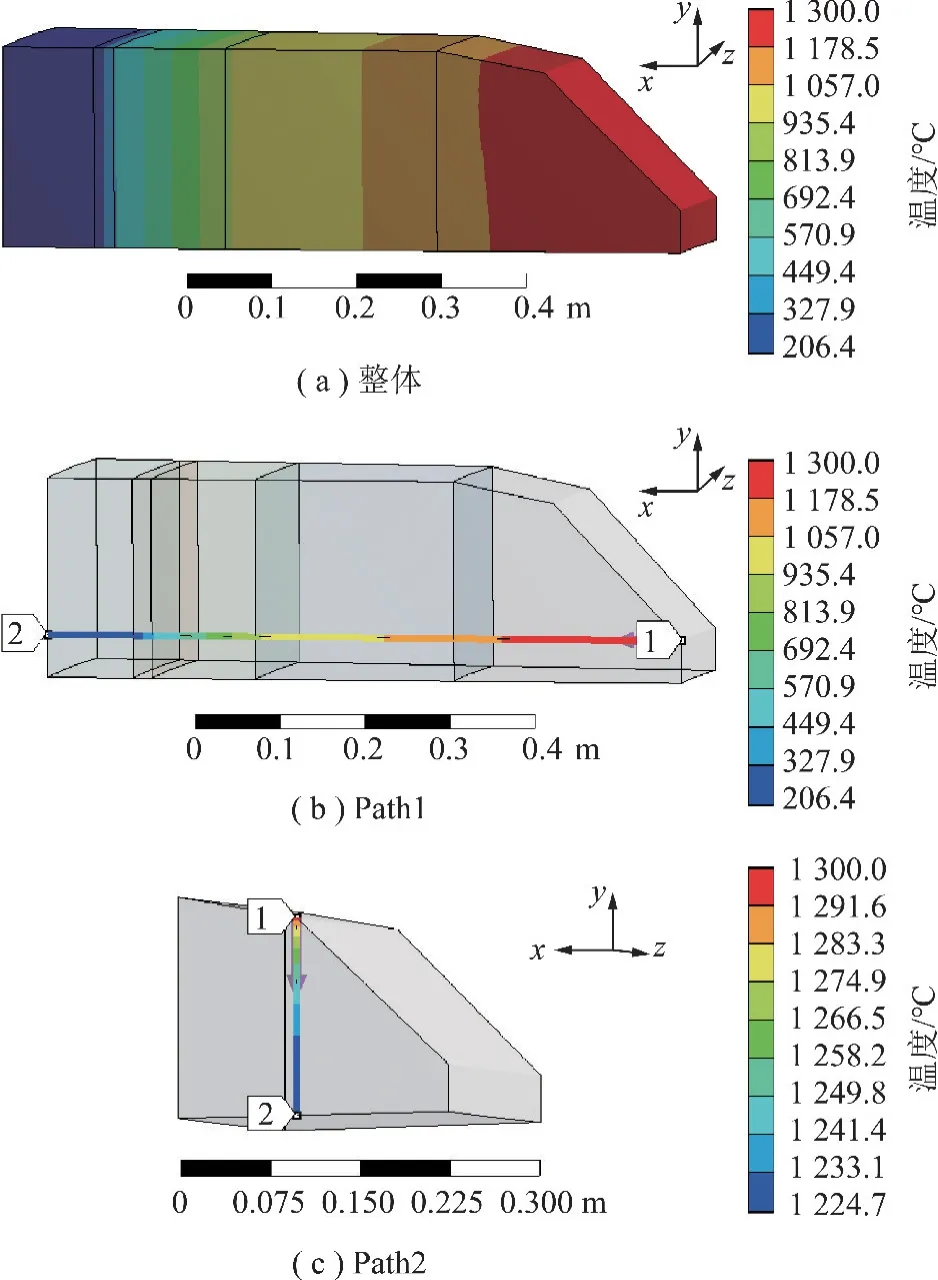
图4 耐火衬里的温度分布云图Fig.4 Temperature distribution of refractory lining
图5为耐火衬里及钢壳的等效应力分布云图,图5(a)为整体耐火衬里及钢壳的等效应力分布云图,可得在K 砖上部拐角处出现应力最大值,K 砖上部整体应力较大为0.850~9.100 GPa。图5(b)为Path1 的等效应力分布线,可明显看出热面砖应力>背衬砖应力>钢壳应力>隔热砖应力,其中热面砖、背衬砖、隔热砖和钢壳的应力分别约为0.850,0.620,0.074,0.410 GPa,陶瓷纤维的应力几乎为0。图5(c)为Path2 的等效应力分布线,可看出由上到下应力逐渐由3.400 减小到0.800 GPa。

图5 耐火衬里的等效应力分布云图Fig.5 Equivalent stress distribution of refractory lining
图6(a)为整体耐火衬里及钢壳的等效应变分布云图,应变用以描述物体的变形程度。由图6(a)可知陶瓷纤维处等效应变最大约为0.210,热面砖、背衬砖和隔热砖的应变非常小不到0.009,且热面砖应变>背衬砖应变>隔热砖应变>钢壳应变,钢壳应变仅为0.002。图6(b)为Path1 的等效应变分布线,可得陶瓷纤维中间处应变最大。图6(c)为Path2 的等效应变分布线,可知热面砖拐角处应变最大,由点1 到点2 方向应变从0.031 逐渐减小到0.008。

图6 耐火衬里的等效应变分布云图Fig.6 Equivalent elastic strain distribution of refractory lining
图7(a)为整体耐火衬里及钢壳的总变形分布云图。工业上OMB 气化炉的热面砖与背衬砖之间一般留有约3 mm 的膨胀缝,背衬砖与隔热砖之间留有约2 mm 的膨胀缝[30-32]。由图7(a)可得热面砖绝对变形量为1.94 mm < 3.00 mm, 背衬砖总变形量3.75 mm,绝对变形量3.75 - 1.94 = 1.81 mm <2.00 mm,表明总变形的模拟计算结果与工业气化炉的数据相符。隔热砖总变形量4.35 mm,绝对变形量仅为4.35-3.75=0.60 mm,远小于热面砖和背衬砖,钢壳的绝对变形量最小只有0.12 mm。图7(b)为Path1 的总变形分布线,可得最大总变形量位于隔热砖与陶瓷纤维之间。图7(c)为Path2 的总变形分布线,可得热面砖由点1 到点2 总变形量逐渐减小,即热面砖受热膨胀后会向上变形,而且拐角处总变形量最大。在炉内高温环境中,筒体砖受热膨胀总体向上变形,变形量不断累加,最终全部集中在K 砖部位,这与工业上在K 砖上部留有15 mm 的膨胀缝相一致。
3.2 不同热端面温度影响
气化炉K 砖部位热端面温度一般在1 250~1 350 ℃[22],以图2结构模型尺寸为基础,热面砖热端面温度分别为1 100,1 200,1 300 以及极限1 400 ℃,比较不同热面砖热端面温度对耐火衬里和钢壳温度、应力、应变及变形量分布的影响。

图7 耐火衬里的总变形分布云图Fig.7 Total deformation distribution of refractory lining
不同热面砖热端面温度对耐火衬里温度分布的影响如图8所示。随着热端面温度的升高,耐火衬里及钢壳整体温度升高,尤其是热面砖、背衬砖温度增加比较明显。当热端面温度从1 100 升高到1 400 ℃时,钢壳外表面温度从177.2 逐渐增加到220.9 ℃,温度变化不超过50 ℃,主要是因为隔热砖和陶瓷纤维能够阻隔大量热量,使得气化炉钢壳温度波动较小。
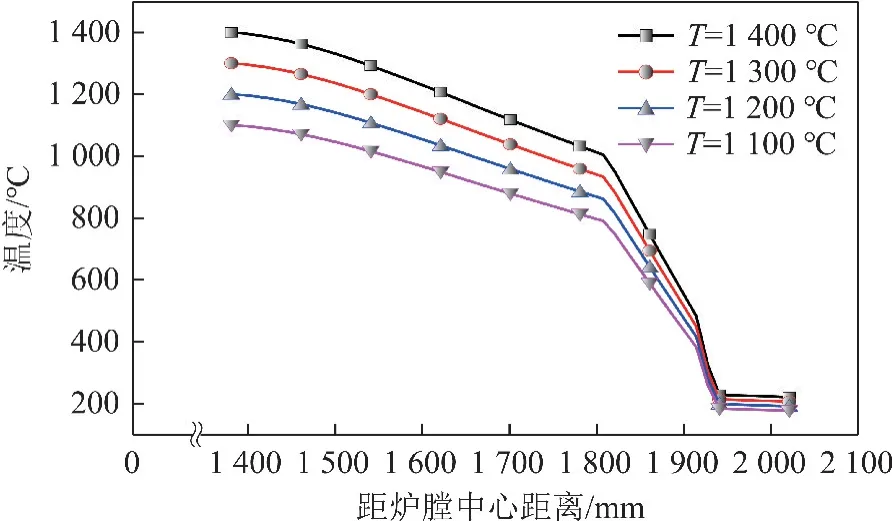
图8 不同热面砖热端面温度下耐火衬里和钢壳的温度分布Fig.8 Temperature distribution of refractory lining and steel shell under different end face temperatures of the hot-face brick
图9为不同热端面温度下耐火衬里的等效应力分布规律。等效应力在热面砖热端面位置出现最大值,即此处最易产生裂纹,如图10所示。从图9可以明显看到距炉膛中心越远,耐火衬里的等效应力呈下降趋势,而且热面砖应力>背衬砖应力>钢壳应力>隔热砖应力,陶瓷纤维应力几乎为0。不同热端面温度下耐火衬里应力变化规律基本一致,热端面温度越高,耐火衬里及钢壳整体应力越大,尤其是热面砖应力增加最为明显。当热面砖热端面温度从1 100 ℃升高到1 400 ℃时,热端面应力从0.68 升高到1.10 GPa。

图9 不同热面砖热端面温度下耐火衬里和钢壳的等效应力分布Fig.9 Equivalent stress distribution of refractory lining and steel shell under different end face temperatures of the hot-face brick

图10 工业OMB 气化炉内热面砖(K 砖)端面处的裂纹Fig.10 Crack on the end face of the hot-face brick(K-brick)in the industrial OMB gasifier
图11为不同热面砖热端面温度下耐火衬里的等效应变分布。图11中尖峰的横坐标位置对应陶瓷纤维,尖峰纵坐标表示陶瓷纤维处的等效应变,可以看到陶瓷纤维处的等效应变迅速变化且数值最大,而且陶瓷纤维的等效应变远远大于耐火砖和钢壳的等效应变。即使热端面温度高达1 400 ℃,热面砖的最大应变也不超过0.01,而陶瓷纤维的最大应变可达到0.23。由放大图可知,热面砖应变>背衬砖应变>隔热砖应变>钢壳应变。在同一温度下,热面砖端面处应变最大,随距炉膛中心距离增加应变先迅速减小,然后几乎保持不变。背衬砖和隔热砖处的应变逐渐减小,钢壳处应变最小。随着热端面温度的升高,耐火衬里及钢壳的等效应变逐渐增加,而且热面砖和背衬砖应变增加幅度更大。

图11 不同热面砖热端面温度下耐火衬里和钢壳的等效应变分布Fig.11 Equivalent elastic strain distribution of refractory lining and steel shell under different end face temperatures of the hot-face brick
不同热面砖热端面温度下热面砖、背衬砖和隔热砖的绝对变形量如图12所示。从图12可以看到热面砖热端面温度从1 400 降低到1 100 ℃时,热面砖绝对变形量逐渐从2.12 减小到1.62 mm。热面砖热端面温度越低,背衬砖绝对变形量越小。热面砖热端面温度从1 400 降低到1 100 ℃,背衬砖绝对变形量逐渐从1.95 减小到1.56 mm。背衬砖与隔热砖绝对变形量的变化趋势与热面砖基本一致,但是隔热砖的绝对变形量相对热面砖和背衬砖而言非常小,当热面砖热端面温度为1 400 ℃时,隔热砖绝对变形量最大且为0.13 mm,当热面砖热端面温度为1 100 ℃时,隔热砖绝对变形量最小仅为0.07 mm。

图12 不同热面砖热端面温度下热面砖、背衬砖和隔热砖的绝对变形量Fig.12 Absolute deformation of hot-face brick,backup brick and heat isolation brick under different end face temperatures of the hot-face brick
3.3 不同热面砖厚度影响
为探究不同热面砖厚度影响,设置热面砖热端面温度为1 300 ℃,分别计算不同厚度下耐火衬里及钢壳的温度、等效应力、等效应变和变形量分布规律。
图13为热面砖厚度对耐火衬里及钢壳温度分布的影响。从图13可以看出,随着热面砖厚度的增加,耐火衬里及钢壳的温度逐渐降低。相比隔热砖,热面砖和背衬砖温度下降更快。当热面砖厚度从60 增加到230 mm 时,钢壳外表面温度从225.9 缓慢降低到206.4 ℃,温度差别仅为19.5 ℃,表明热面砖厚度对钢壳外表面温度影响较小。

图13 不同热面砖厚度下耐火衬里及钢壳的温度分布Fig.13 Temperature distribution of refractory lining and steel shell under different thickness of the hot-face brick
图14为热面砖厚度对耐火衬里及钢壳等效应力分布的影响。由图14可知热面砖越厚,耐火衬里及钢壳等效应力越小,该结果与文献[17]相一致。热面砖和背衬砖应力随热面砖厚度增加迅速减小,而隔热砖和钢壳应力变化较小。当热面砖厚度大于180 mm 时,热面砖热端面处应力最大,距炉膛中心越远,热面砖应力先迅速减小然后基本持平;当热面砖厚度小于180 mm 时,热面砖热端面处应力较小,距炉膛中心越远,热面砖应力先迅速增加然后几乎保持不变。当热面砖厚度为180 mm 时,热面砖整体应力大小适中,而且分布均匀没有明显突变,表明当热面砖厚度为180 mm 时,热面砖结构最优,最有利于提高耐火衬里尤其是热面砖的使用寿命。
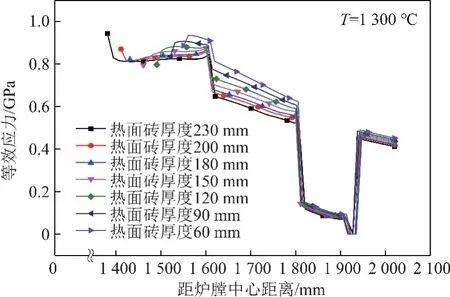
图14 不同热面砖厚度下耐火衬里及钢壳的等效应力分布Fig.14 Equivalent stress distribution of refractory lining and steel shell under different thickness of the hot-face brick
不同热面砖厚度下耐火衬里及钢壳的应变分布如图15所示,图15表明陶瓷纤维处应变最大,热面砖、背衬砖和隔热砖应变较小不超过0.009,且钢壳应变最小仅为0.003。由放大图可看到,随着热面砖厚度的增加,耐火衬里的应变逐渐减小,尤其是背衬砖区域应变减小趋势最快。当热面砖厚度大于180 mm 时,距炉膛中心越远,热面砖应变先减小后增加,当热面砖厚度小于180 mm 时,距炉膛中心越远,热面砖应变先迅速增加然后基本保持不变。应变结果与图14中的应力结果的变化规律基本一致,进一步说明热面砖厚度180 mm 是一个比较优化的结构尺寸。
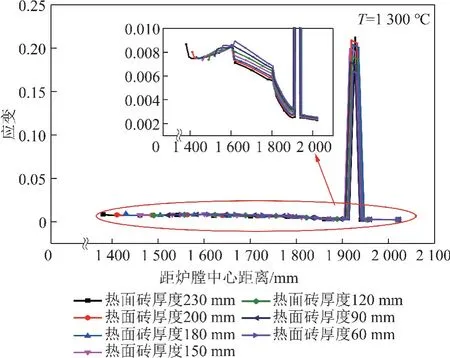
图15 不同热面砖厚度下耐火衬里及钢壳的应变分布Fig.15 Equivalent elastic strain distribution of refractory lining and steel shell under different thickness of the hot-face brick
图16为不同热面砖厚度下热面砖、背衬砖和隔热砖的绝对变形量。从图16可以看到热面砖厚度从60 mm 增加到230 mm,热面砖绝对变形量逐渐从0.75 mm 增加到1.95 mm。背衬砖绝对变形量的变化趋势与热面砖正好相反,可以看到热面砖越厚,背衬砖绝对变形量越小。热面砖厚度为60 mm 时,背衬砖绝对变形量最大且为2.03 mm,热面砖厚度为230 mm 时,背衬砖绝对变形量最小仅为1.81 mm。隔热砖绝对变形量的变化趋势比较复杂,由于隔热砖区域温度较低,隔热砖绝对变形量较小且不超过1 mm。当热面砖厚度为180 mm 时,隔热砖绝对变形量最小仅为0.02 mm,当热面砖厚度为150 mm 时,隔热砖绝对变形量最大也只有0.61 mm。总体来说,随着热面砖厚度从60 mm 增加到230 mm,热面砖绝对变形量逐渐增大,背衬砖绝对变形量逐渐减小,且热面砖变形率大于背衬砖变形率。当热面砖厚度增加,背衬砖绝对变形量最大,热面砖绝对变形量次之,隔热砖绝对变形量最小。
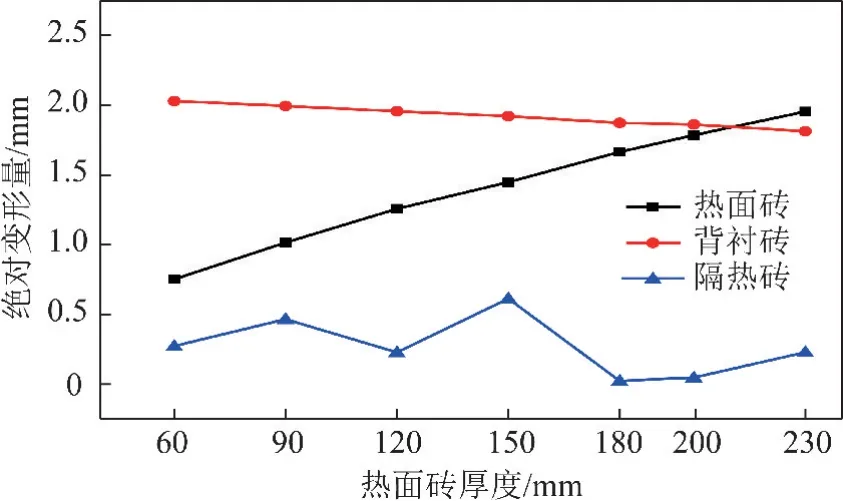
图16 不同热面砖厚度下热面砖、背衬砖和隔热砖的绝对变形量Fig.16 Absolute deformation of hot-face brick,backup brick and heat isolation brick under different thickness of the hot-face brick
4 结 论
(1)当热面砖(K 砖)热端面温度为1 300 ℃时,热面砖与背衬砖之间温度为1 131.2 ℃,背衬砖与隔热砖之间温度为929.7 ℃,隔热砖与陶瓷纤维之间温度为441.8 ℃, 陶瓷纤维与钢壳之间温度为214.2 ℃,钢壳外表面温度为206.4 ℃,模拟计算结果能够与工业数据较好吻合。热面砖上部拐角处应力最大,陶瓷纤维应力几乎为0,热面砖应力>背衬砖应力>钢壳应力>隔热砖应力。热面砖应变>背衬砖应变>隔热砖应变>钢壳应变。热面砖和背衬砖的绝对变形量分别为1.94 和1.81 mm,而隔热砖的绝对变形量仅为0.6 mm,远小于热面砖和背衬砖。钢壳总变形量最小只有0.12 mm。
(2)热面砖热端面温度升高,耐火衬里及钢壳整体温度升高,等效应力、等效应变也都相应增大。当热端面温度从1 100 升高到1 400 ℃时,对于3 种耐火砖而言,热面砖的温度、应力、应变和绝对变形量增幅均最大。在同一温度下,等效应力和等效应变在热面砖热端面位置均出现最大值,即此处最易产生裂纹。
(3)随着热面砖厚度的增加,耐火衬里及钢壳的温度、等效应力和等效应变逐渐降低,但是热面砖绝对变形量逐渐增大。相比隔热砖和钢壳,热面砖和背衬砖的温度和应力随热面砖厚度的增加下降更快。当热面砖厚度为180 mm 时,热面砖整体应力大小适中且分布均匀,而且应力结果与应变结果的变化规律基本一致,表明热面砖最优的厚度尺寸为180 mm,该结构有利于提高热面砖的使用寿命。
