玄武岩纤维棒聚合物混凝土的弯曲韧性

崔圣爱， 徐李麟， 饶家锐， 曹卓颖

（西南交通大学 土木工程学院，四川 成都， 610031）

作为水泥混凝土的替代品，聚合物混凝土（PC）广泛应用于排水系统、桥面铺装层等领域［1‑3］.适量的聚合物能促进水泥水化，使PC具有优良的力学性能.这一方面归因于聚合物成膜后使PC内部微裂纹与应力集中减少，另一方面可能与聚合物增强界面的化学键强度有关［4‑5］.但过量的聚合物反而导致PC的力学性能降低［6‑7］，比如锦江桥和成龙大道桥裂损后桥面修补比例高达61.2%和63.3%.因此，亟需改善PC的韧性，提高其抗裂性.

掺入纤维能提高复合材料的力学性能［8‑10］，且与纤维增强指数IR（纤维掺量与长径比的乘积）有关［11］.在微观层面上，纤维承载并传递了基体中形成的部分应力，纤维的桥接作用阻止了基体中微裂纹的发展；在宏观层面上，纤维通过抑制基体中微裂纹的发展来提高其吸收能量的能力.玄武岩纤维棒（BFB）是一种绿色环保纤维，且弹性模量和抗拉强度较高.掺入聚酰胺树脂包裹的玄武岩纤维束，试件达到峰值荷载后仍有较高的残余强度和延性［12］.

鉴于此，本文研究了不同聚灰比mP/mC（质量比，文中涉及的含量、比值等除特殊说明外均为质量分数或质量比）和IR条件下玄武岩纤维棒聚合物混凝土（BFB‑PC）的弯曲韧性，分析了IR对其韧性指标T2（n-1）（n）（n为未掺纤维试件峰值荷载对应挠度的倍数）的影响，探究了T2（n-1）（n）与裂缝形貌的关系，并建立了BFB‑PC的弯曲韧性计算模型，以期为高韧性聚合物混凝土的设计提供理论依据.

1 试验

1.1 原材料与配合比设计

水泥（C）为P·O 42.5普通硅酸盐水泥；骨料为细度模数2.7的中砂（S），级配区为Ⅱ区；聚合物（P）为丁苯乳液，固含量为50%，黏度为2 300 mPa·s；消泡剂（DA）为聚醚改性硅消泡剂，用于减少因丁苯乳液掺入而引入的气泡；减水剂为减水率25%以上的聚羧酸减水剂；拌和水（W）为自来水.硅灰（SF）的SiO2含量为96.04%；微珠（CP）的SiO2、Al2O3和Fe2O3的总含量为82.45%.BFB由400根玄武岩纤维单丝和树脂包裹组成，长度lf为12、15 mm，直径df为0.4 mm，密度为2 000 kg/m3，抗拉强度为2 300 MPa.设置BFB‑PC的mP/mC为0、0.06，胶砂比为0.33，水胶比为0.35，BFB的体积分数φf为0%、1%、2%、3%，经试拌确定减水剂的掺量为1.8%，硅灰及微珠掺量均为胶凝材料的5.0%.BFB‑PC的配合比见表1.

表1 BFB-PC的配合比Table 1 Mix proportions of BFB-PC

1.2 试验方法

1.2.1 试件成型及养护

将BFB、胶凝材料及砂放入搅拌锅内搅拌，待材料混合均匀且纤维分散后，缓慢加入含减水剂、丁苯乳液和消泡剂的水.成型尺寸为40 mm×40 mm×160 mm的胶砂试件，装模后覆盖1层不透水薄膜，防止水分散失.24 h后拆模放入标准养护室养护至7 d取出，再转入室内自然养护至规定龄期.

1.2.2 四点弯曲试验

四点弯曲试验能模拟许多工程中构件的受力情况，为了更直观地展现纤维增强水泥基复合材料的弯曲韧性，设置试件的净跨高比为3，龄期28 d.根据CECS 13—2009《纤维混凝土试验方法标准》进行四点弯曲试验，使用RTM305D型微机控制电子万能试验机加载，加载速率为0.1 mm/min，利用荷载传感器和LVDT测量弯曲荷载与跨中挠度.

2 结果与讨论

2.1 荷载-挠度曲线

试件的荷载-挠度（P‑δ）曲线见图2.由图2可见，掺入BFB后，BFB‑PC由脆性断裂转变为延性破坏，部分工况表现出明显的挠曲软化行为，具有更高的剩余承载力.由于BFB‑PC峰后软化曲线较长，荷载难以降至0 N，故当挠度达到5.5 mm时停止加载，弯曲韧性为荷载-挠度曲线在挠度为0～5.5 mm下的面积.与试件P0B0相比，试件P0B2‑15、P0B3‑12的弯曲韧性分别提升了5.35、8.39倍，韧性提升显著.

图1 试件的荷载-挠度曲线Fig.1 P‑δ curves of specimens

图2 BFB‑PC的T2（n-1）（n）Fig.2 T2（n-1）（n） of BFB‑PC

2.2 弯曲荷载下的韧性指标

采用鞠杨法［13］评估BFB‑PC的韧性，该方法属于能量比值法.韧性指标T2（n-1）（n）是评价纤维混凝土梁、板弯曲韧性的相对指标，该值反应梁或板在四点弯曲荷载作用下的延性与吸收能量的大小.将未掺纤维试件峰值荷载下的挠度δmax作为荷载-挠度曲线的初始参考变形来计算T2（n-1）（n），其计算式为：

式中：n取值3、5、7、10；Eunrein为不掺纤维试件荷载-挠度曲线下的面积；Enδmax为给定挠度下荷载-挠度曲线下的面积.

试件尺寸与加载方式不变时，δmax和Eunrein为材料常数，与纤维掺量无关［14］.P6B0和P0B0的δmax分别为0.365、0.358 mm.BFB‑PC的T2（n-1）（n）见图2.由图2可见：T2（n-1）（n）与IR呈二次函数关系，这与文献［14］的研究结果一致；当mP/mC=0.06时，相关系数R2＞0.800；当mP/mC=0时，除了T4（3）外，R2＞0.900；T18（10）和T12（7）的相关系数较高，T8（5）和T4（3）的相关系数较低，T2（n-1）（n）与IR在大挠度阶段的相关性更好；当mP/mC=0.06时，BFB‑PC的T2（n-1）（n）高于其在mP/mC=0时，这与聚合物的掺入提高了纤维与基体界面黏结性能有关［15‑16］.

由图2还可见：当IR＜90.0时，T2（n-1）（n）随着IR的增大而增大，更多、更长的纤维有利于桥接基体裂缝并消耗能量，从而增强BFB‑PC的弯曲韧性；T2（n-1）（n）的增长率随着n的增大而增大，其中T4（3）的增长率最低，T18（10）的增长率最高，这是因为在初裂阶段，裂缝扩展较小，BFB尚未充分发挥作用.随着加载的继续进行，挠度增大，纤维抑制裂缝进一步扩展，并起桥接裂缝的作用；IR=90.0是BFB的增韧阈值，当IR＞90.0时，不论聚灰比和n取值如何，T2（n-1）（n）开始减小，因为BFB的长度或体积分数过高时，纤维难以分散均匀，从而导致基体内部薄弱面和缺陷增多，使得抗弯性能下降；IR=37.5是另一个阈值，当IR＜37.5时，少量BFB对聚合物混凝土的韧性提升有限，试件的弯曲韧性受基体控制.

2.3 韧性指标与裂缝形貌的关系

T2（n-1）（n）随IR增大而增大，同时BFB‑PC的裂缝扩展路径与裂缝形貌变得更加曲折、复杂.通过分形理论可以建立分形维数与材料特性之间的关系，有效描述混凝土裂缝形态的复杂程度，因此大量应用于断口、裂纹等领域［17‑18］.BFB‑PC的裂缝形貌与弯曲韧性存在一定的关系，为进一步分析IR与试件在大挠度下裂缝形貌的关系，采用盒计数法定量描述裂缝的分形特征.将若干个边长为r的盒子覆盖所有裂缝，计算非空盒子的数量，通过改变r形成若干盒子，计算包含裂缝的最小非空盒子数Nr，经多次变换r，求出不同的Nr和1/r，将二者取对数进行线性回归，所得直线斜率的绝对值为裂缝分形维数Dbox：

通过Matlab计算BFB‑PC的裂缝分形维数，提取裂缝图像，将原始图转换成灰度图，并对灰度图进行二值化处理.当mP/mC=0.06时，BFB‑PC的裂缝灰度图见图3.由图3可见：当IR=0（不掺BFB）时，试件呈脆性破坏，断口面平整，裂缝垂直于拉伸方向；当IR=37.5时，裂缝面积增大，扩展路径更加曲折，这表明试件破坏时的变形能力与耗能能力提升，这也是BFB‑PC弯曲韧性提高的重要原因；当IR增大到75.0、90.0时，裂缝复杂程度进一步提升，这与BFB‑PC的挠曲软化行为对应；由于纤维的存在，试件破坏后并没有完全断开.

图3 BFB‑PC的裂缝灰度图Fig.3 Grey images of cracks in BFB‑PC（mP/mC=0.06）

BFB‑PC裂缝分形维数与T2（n-1）（n）的关系见图4.由图4可见：T2（n-1）（n）与裂缝分形维数呈二次函数关系，且T2（n-1）（n）随着分形维数的增大而增大，这表明裂缝形貌越复杂，BFB‑PC开裂时消耗的能量越多，韧性指标越大；相关系数随着n的增大而增大，当mP/mC=0.06时，T18（10）的相关系数最大，T4（3）的相关系数最小.值得注意的是，本文计算的是BFB‑PC破坏后的裂缝分形维数，因此其与试件在大变形下的韧性指标相关性更好.与mP/mC=0的BFB‑PC（未掺聚合物）相比，mP/mC=0.06的BFB‑PC相关系数更高，且其裂缝形貌复杂程度相对较低，裂缝分形维数更小.

图4 BFB‑PC裂缝分形维数与T2（n-1）（n）的关系Fig.4 Relationships of Dbox and T2（n-1）（n） of BFB‑PC

2.4 弯曲韧性计算模型

根据文献［19］计算纤维体积分数为1%、2%BFB‑PC的弯曲韧性.当复合材料中纤维取向与混凝土主拉应力方向一致时，才能发挥BFB的最佳补强效果，但实际并非如此，故计算时考虑纤维的取向系数η0.另外，由于纤维的不连续性，纤维会随着基体产生裂缝而滑移，故计算时还需要考虑纤维的长度有效系数ηl［20］.

无序分布的纤维取向系数η0可通过计算得到.由于边界效应的影响，复合材料中单根纤维的η0与其到试件边缘的距离有关.假定纤维几何中心到试件边缘的距离为αlf（0＜α＜1），α与取向系数η0的关系见图5［21］.

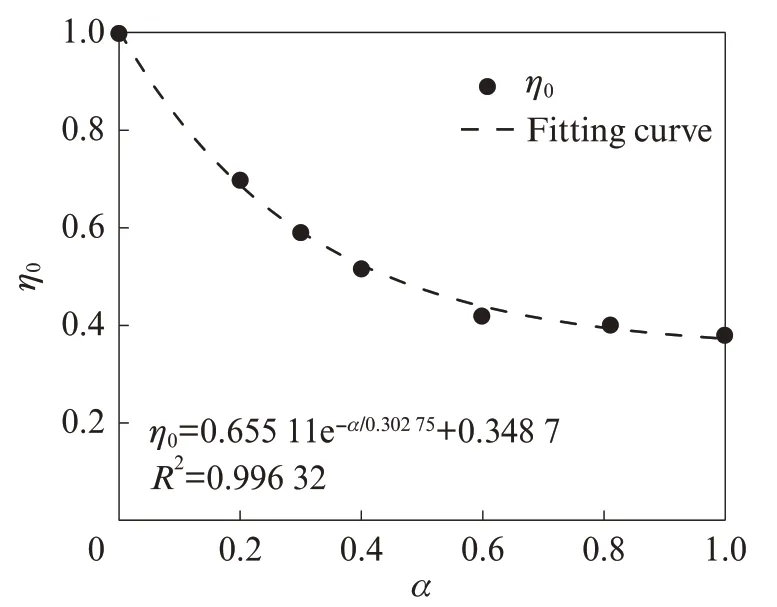
图5 边界效应对纤维取向系数的影响Fig.5 Influence of boundary effect on fiber orientation coefficient［21］

当试件宽度t＞2lf时，BFB‑PC中BFB的纤维取向系数平均值与t、lf的关系为［21］：

由计算可得，当lf为12、15 mm时，BFB的η0分别为0.474 0、0.498 8.

当BFB‑PC失效时，BFB的拔出或拔断与其长度密切相关，文献［22］明确了纤维承受的拉应力与其长度的关系.当纤维长度lf小于其临界长度时，试件破坏时纤维被拔出；当时，BFB‑PC中间处出现裂缝时，纤维被拔断，否则纤维从短的嵌入侧拔出；当试件破坏时纤维被拔断.

当BFB‑PC产生裂缝后，荷载开始向BFB上转移，直至纤维从基体中拔出或拔断.由BFB‑PC的抗拉强度［19］可得基体与BFB的平均界面黏结强度τ为：

纤维增强混凝土的抗弯强度与抗拉强度呈线性关系.为简便计算，文献［23］中纤维增强混凝土抗弯强度的关系为：

BFB的长度有效系数ηl为［24］：

结合式（4）～（7），BFB的临界长度为：

将单根BFB的平均功［20］与单位体积BFB‑PC中BFB的数量N相乘，得到弯曲韧性增量Wa.Wa和N的计算式为：

由于试件破坏后没有直接断开，这表明并非所有BFB都参与抑制裂缝扩展，因此引入高缝比β（试件高度与裂缝长度的比值）来计算BFB的数量效率.通过Image J测量试件裂缝的长度，结果取平均值.综上，得到修正后的BFB‑PC弯曲韧性增量Wa为：

文中挠度指LVDT测得梁的跨中变形，试验中定义荷载-挠度曲线总积分面积得到的弯曲韧性为极限弯曲韧性.根据荷载-挠度曲线的积分面积计算试件破坏时吸收的能量.

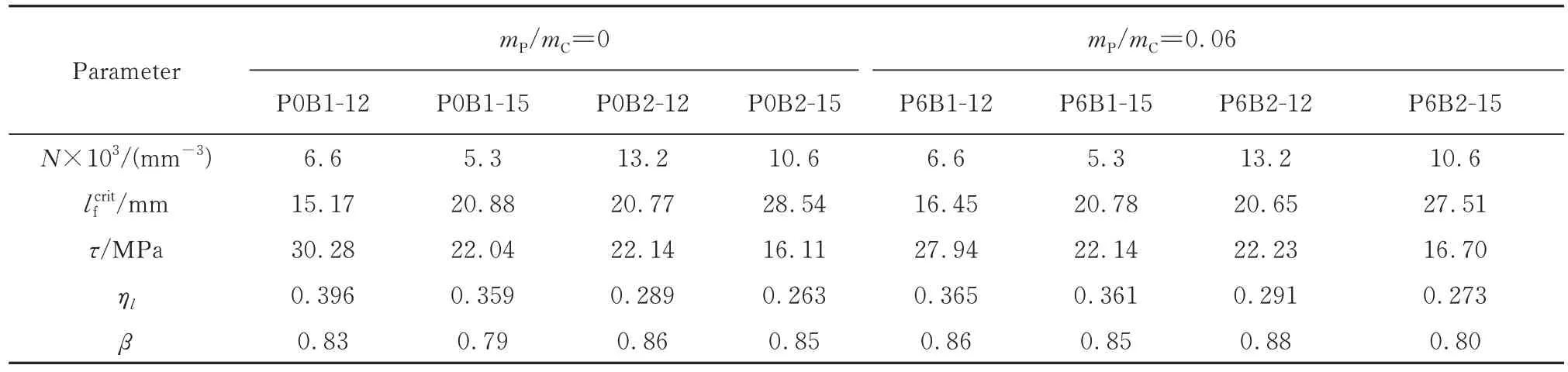
表2 BFB-PC梁的弯曲韧性理论参数Table 2 Theoretical parameters of flexural toughness for BFB-PC beams

BFB‑PC梁的弯曲韧性增量见图6.由图6可见，BFB‑PC梁的弯曲韧性增量理论值与通过荷载-挠度曲线得到的试验值间的相对误差均小于15.00%，其中试件P0B2‑12的相对误差最大，为12.75%.综上，本文所建立的弯曲韧性计算模型可以准确描述BFB对PC梁的增韧作用.

图6 BFB‑PC梁的弯曲韧性增量Fig.6 Increment value of flexural toughness of BFB‑PC beams

3 结论

（1）BFB的增韧阈值为IR=37.5和IR=90.0.当37.5≤IR≤90.0时，纤维增强指数IR和聚灰比对BFB‑PC的韧性指标T2（n-1）（n）产生正面影响；当IR＜37.5时，少量BFB对BFB‑PC的韧性提升有限；当IR＞90.0时，BFB‑PC的T2（n-1）（n）随着IR的增大而减小.与不掺BFB相比，当IR=90.0时，BFB对BFB‑PC的增韧效果最优，其弯曲韧性提升了8.39倍.随着IR的增大，BFB‑PC从脆性断裂转变为延性破坏，部分工况表现出明显的挠曲软化行为，具有更高的剩余承载力.

（2）T2（n-1）（n）与IR之间存在二次函数关系，且T2（n-1）（n）与IR在大挠度阶段具有更好的相关性.随着n的增大，T2（n-1）（n）的增长率增大.当IR相同，BFB‑PC聚灰比为0.06且T2（n-1）（n）高于其未掺聚合物时，掺入丁苯乳液可改善BFB与基体的界面黏结性能.

（3）随着IR的增大，BFB‑PC的裂缝形貌发生变化，裂缝扩展路径从直线变得非常曲折，且裂缝形貌越复杂，BFB‑PC开裂时消耗的能量越多.T2（n-1）（n）与裂缝分形维数呈二次函数关系，当IR＜90.0时，T2（n-1）（n）随着分形维数的增大而增大，相关性随n的增大而增大.

（4）建立了考虑纤维取向系数、长度有效系数的BFB‑PC弯曲韧性计算模型，理论值与试验值的相对误差均小于15.00%.故本文计算模型可靠，能够很好地描述BFB对PC梁的增韧作用.