基于伪解析法的TTI介质纯qP波地震波场正演模拟
2024-03-06张奎涛廖家荣顾汉明孙瑛莹陈怿旸王凯
张奎涛,廖家荣,顾汉明,孙瑛莹,陈怿旸,王凯
(1.江西省交通设计研究院有限责任公司,江西 南昌 330052; 2.中国地质大学(武汉) 地球物理与空间信息学院,湖北 武汉 430074)
0 引言
实际地下介质充满流体、裂缝及裂隙,因而表现出各向异性特征,这种现象也在实验室和波场测量中被观测到[1],使得各向异性成为地震波场数值模拟中越来越不容忽略的因素。
进行弹性波数值模拟时,得到的混合波场通常同时含有纵波和横波,而在进行地震偏移成像,尤其是弹性波逆时偏移成像时,须将纵、横波解耦,以得到物理意义明确的成像剖面[2]。为此,Alkhalifah[3-4]提出了声学近似假设下的拟声波方程,人为设定沿对称轴方向的横波速度为零,推导出标量形式的四阶微分方程。为了简化方程,提高计算效率,Du等[5]和Zhou等[6]通过不同的降阶方法,推导出不同形式的二阶耦合qP波微分方程。Duveneck等[7]从胡克定律和运动方程出发,推导得到另一种形式的拟声波方程,且其波场具有明确的物理意义。程玖兵等[8-9]推导得到各向异性介质的伪纯模式波动方程,使其在运动学上同弹性波动方程等价。
上述各方法均存在拟声波方程的突出缺点,即当模型参数中有变化较大的倾角和方位角时,会出现不稳定的现象[10]、残留着横波假象[11],或只有在Thomsen参数满足ε≥δ时正演模拟才是稳定的[12]。为了解决此类问题,有学者另辟蹊径,从qP波与qSV波的频散关系出发,直接解耦以构建纯qP波控制方程。要实现qP与qSV波的完全分离,关键在于导出简单、灵活的纯qP波控制方程和设计有效的拟微分求解算法。例如,Du等[5]和Zhang等[13]基于弱各向异性近似和平方根近似,推导出一种纯qP波解耦方程,其表现为时间—波数域形式,能较准确地描述TTI介质中的运动学特征;Zhan等[14]推导了一种新的解耦方程,将P波与SV波完全分离开来,并成功将其应用于逆时偏移中;Xu等[15]提出了一种纯qP波椭圆微分方程,通过将微分方程分解成一个标量算子和一个微分算子,并用椭圆分解方法修正标量算子,达到校正振幅误差的目的;胡书华等[16]则将Xu等[15]二阶微分方程做降阶处理,通过Lebedev交错网格,得到TTI介质下纯qP波的稳定传播;张庆朝等[17]利用近似相速度公式,导出TTI介质三维qP波频散方程及波动方程,并使用伪谱法做正演模拟;顾汉明等[18]将各向异性介质推广到黏声各向异性介质,通过Low-rank方法,实现了黏声各向异性介质纯qP波正演模拟。
纯qP波波动方程中往往存在着拟微分算子,谱方法能够较好地进行求解。伪谱法(pseudo spectral method,PSM)是一种早期发展出来的谱方法[19],其基本思想是通过傅里叶变换方法计算波场对空间的导数,在时间域通过有限差分法计算波场对时间的导数。正因如此,使得伪谱法具有非常高的空间精度,没有误差累积效应和空间频散,是一种较为理想的数值模拟方法。由于伪谱法计算时间导数时采用的是有限差分,使得其具有时间频散,为了解决这一问题,Etgen等[20]提出了伪解析算法,其基本思想是波数域推导时间误差补偿因子并作用于拉普拉斯算子,从而补偿在伪谱法中因时间导数的二阶差分造成的误差,达到进一步提高数值模拟精度的目的;Chu等[21]在Etgen提出的伪解析法的基础上,提出了归一化伪拉普拉斯算子的伪解析法,随后,张衡等[22]将这一方法运用于解耦的TTI介质波动方程中,得到了高精度的地震波场,在时间和空间上能够同时达到Nyquist频率。
本文在前人的研究基础上,将qP波拟微分方程变换到空间—波数域,并通过坐标变换,推导了时间域TTI介质二阶纯qP波波动方程,引入伪解析算法,实现了基于伪解析法的TTI介质纯qP波地震波场正演模拟。通过简单和复杂模型测试,验证了本文方法的正确性及对复杂介质的适用性。
1 时间域TTI介质二阶纯qP波波动方程
为了推导本文的TTI介质纯qP波方程,首先从如下VTI介质qP波标量方程

(1)
出发[23]。式中,Q为拟微分算子,其具体表达式为
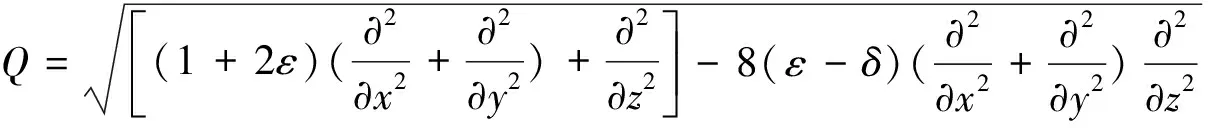
(2)
式中:t为时间坐标;x、y、z为空间坐标;p为地震波场;v0为qP波垂直速度;ε、δ为Thomsen参数。
式(1)控制着VTI介质中qP波的传播,其中所有参数都是随空间变化的,且与混合波场中纵波有着一样的频散关系,即相位相同,能够准确地表征其运动学特征。
将式(1)变换到频率—波数域中有

(3)
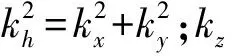
将式(3)改写为
(4)
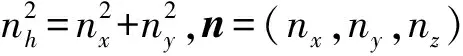

(5)
将式(4)重新改写为
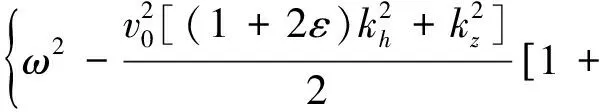
(6)
记椭圆微分算子Se为
(7)
则将式(6)变换到时间域有
(8)
二维情况下有
(9)
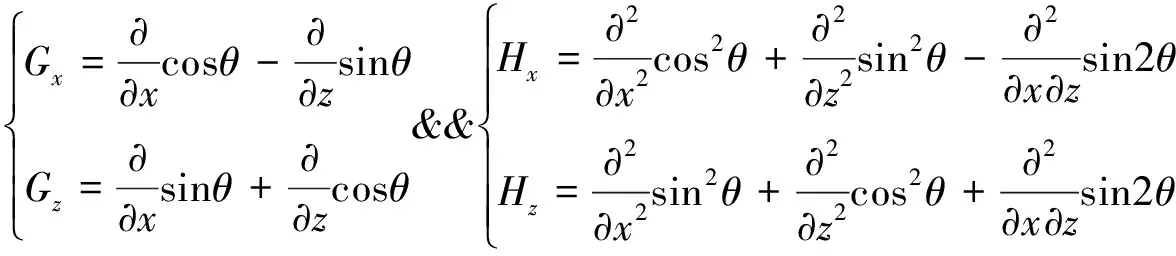
(10)
式中:θ为TTI介质中的极化角;Gx、Gz分别为x、z方向经过坐标旋转后新的一阶微分算子;Hx、Hz分别为x、z方向经过坐标旋转后新的二阶微分算子。
将式(10)代入式(9)中即可得到二维TTI介质纯qP波方程:

(11)
式(11)克服了拟声波方程的局限性,消除了伪横波干扰,不受模型参数限制且地震波场能稳定传播,能够准确地表征地震波场的运动学特征。
伪谱法可以很好求解式(11),即有
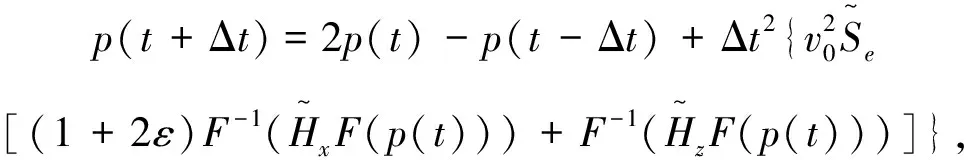
(12)
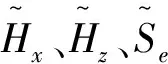
(13)
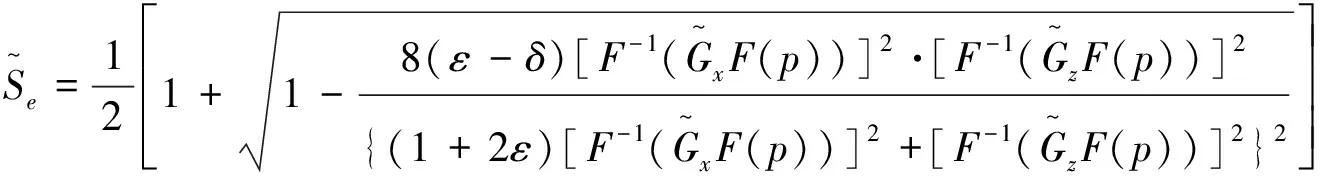
(14)
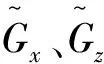
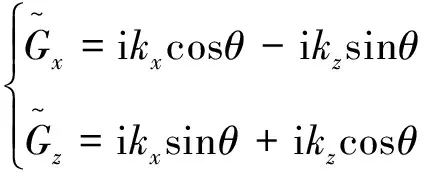
(15)
2 伪解析法
在用伪谱法进行数值模拟时,虽然在空间方向能达到一个波长两个采样点的Nyquist谱精度,但波场对时间的导数仍用有限差分方法计算。因此,在时间方向上仍存在时间频散。而另一种谱方法,即伪解析方法(pseudo analytical method,PAM)能够较好地解决上述问题,并且相比于伪谱法,精度能够进一步提高,使得空间和时间方向上均无频散。其主要思想是在波数域通过修正拉普拉斯算子来达到对时间方向上的有限差分离散误差进行补偿的目的。
对于二阶声波方程,有
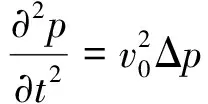
(16)
其二阶时间离散形式有
本文提出一种抗盲检测直扩隐蔽信号设计方法,提出基于数据分级的大信号掩盖技术,给出了波形参数设计方案,并对大信号掩盖下的机密信号解调BER的理论值进行推导.最后仿真验证了所提方案可实现机密信号的抗盲检测.同时在保证机密信号抗盲检测能力的情况下,解调损失可控制在接受范围内.未来工作将分析初始相位、扩频码等参数对信号抗截获的影响.

(17)
对上式进行傅里叶变换并利用时移定理有
(18)
化简上式并代入ω=v0|k|有
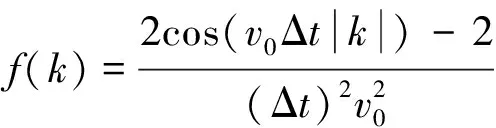
(19)
因此,式(17)的伪解析法为
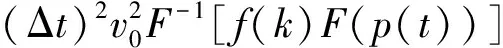
(20)
定义归一化伪拉普拉斯(NPL)算子[21]有

(21)
则式(17)的NPL伪解析法为

(22)
故,式(11)的伪解析法格式为
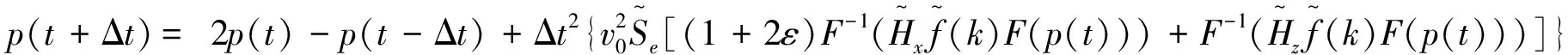
(23)
伪解析法能够准确地补偿时间方向二阶差分所造成的误差,得益于其一个重要特性,即归一化伪拉普拉斯算子的空间导数项随速度的变化缓慢,使得其能够较为准确地补偿时间方向上的误差。为了说明其空间导数项随速度变化缓慢的特点,采用速度1 500 m/s和3 000 m/s作为对比,时间步长为0.001 s,选择波数范围为[0,0.21]。图1为不同速度时的归一化伪拉普拉斯(NPL)算子;图2为基于归一化伪拉普拉斯算子的各类空间二阶导数,包括x方向二阶导数、z方向二阶导数、xz方向混合二阶导数及拟微分算子;图3为基于Hess复杂介质模型的归一化伪拉普拉斯算子。从图1~3中可以发现,归一化伪拉普拉斯算子及各类空间二阶导数均随速度变化缓慢,能够适应较复杂介质。
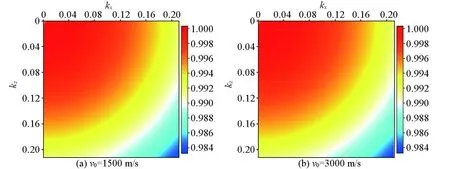
图1 归一化伪拉普拉斯(NPL)算子Fig.1 Normalized pseudo-Laplace(NPL) operator
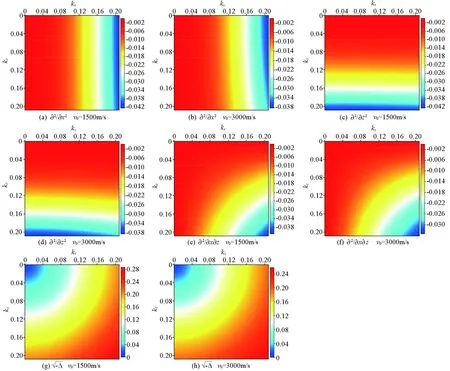
图2 基于归一化伪拉普拉斯(NPL)算子的空间二阶导数Fig.2 A second derivative of space based on normalized pseudo-Laplace(NPL) operators
3 模型试算
3.1 均匀模型
为了验证本文构建的二维TTI介质纯qP波方程不受模型参数的限制,且无伪横波干扰,设计了尺寸为2 000 m×2 000 m的均匀介质模型。其空间网格大小为5 m×5 m,时间步长为1 ms,总时间采样点数为1 000,记录长度为1 s;纵波震源位于模型中心,采用主频为25 Hz的Ricker子波震源;边界条件为海绵边界条件;接收排列范围是0~2 000 m,排列深度为750 m,道间距为10 m,共201道接收。其均匀介质弹性参数见表1。
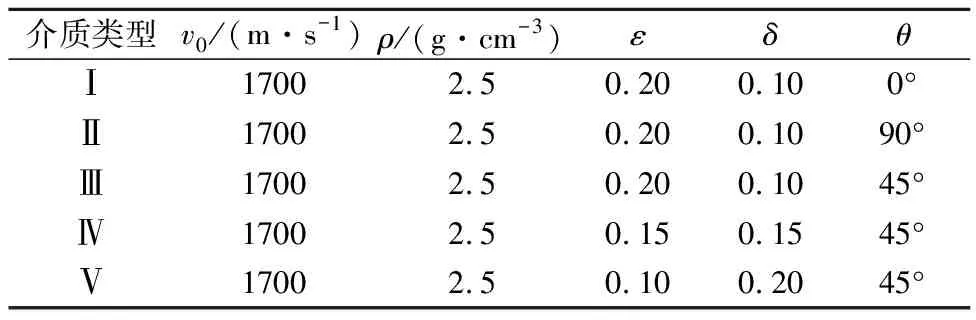
表1 均匀介质模型参数Table 1 Homogeneous media model parameters
图4上部为声学TTI介质常规拟声波方程分别在介质类型Ⅲ(图4a)、Ⅳ(图4b)、Ⅴ(图4c)时400 ms时刻波场快照,图4下部为声学TTI介质纯qP波方程分别在介质类型Ⅲ(图4d)、Ⅳ(图4e)、Ⅴ(图4f)时400 ms时刻波场快照。从图中可见常规拟声波方程(即直接将横波速度设为0)在ε>δ时虽能稳定传播,但会出现菱形假象,严重干扰了有效波;在ε<δ时会出现不稳定现象;只有在ε=δ时才能稳定传播且无假象,这样就极大地限制了其应用。而本文构建纯qP波方程(图4下部),无论是ε<δ、ε>δ还是ε=δ时,都能稳定地传播且不受横波干扰,表明本文方法突破了该限制,具有更强适用性。

a、d—对应介质类型Ⅲ; b、e—对应介质类型Ⅳ; c、f—对应介质类型Ⅴ
图5为纯qP波方程分别在介质类型Ⅰ、Ⅱ、Ⅲ时400 ms时刻波场快照。对比VTI(图5a)、HTI(图5b)和TTI(图5c)3种介质结果发现,通过引入坐标旋转,使得TTI介质具有更强适用性,更能反映实际地下真实介质的情况。

a—介质类型Ⅰ; b—介质类型Ⅱ; c—介质类型Ⅲ
为了说明伪解析法的计算精度,设计了大小为2 000 m×2 000 m的均匀介质TTI模型,空间网格间距为5 m×5 m,时间步长1 ms,采用60 Hz主频的Ricker子波,采用海绵边界条件,纵波震源位于模型中心,模型参数为纵波波速为1 700 m/s,ε=0.25,δ=0.1,θ=45°,由于60 Hz主频的Ricker子波最大频率约为150 Hz,最大纵波速度为1 700 m/s,空间网格间距为5 m,因此一个波长内的采样点数约为1700/150/5=2.2个,基本达到了Nyquist采样定理极限精度的要求。
图6为使用不同方法得到的350 ms时刻纯qP波波场快照,其中6a为有限差分方法、6b为伪谱法和6c为伪解析法。对比这3种方法可以看到,有限差分方法出现明显的频散现象,这是有限差分在时间和空间方向的误差造成的;而伪谱法虽然在空间方向上能够得到Nyquist谱精度,但由于时间方向上的二阶近似误差,使得其仍出现了较为明显的频散;而图6c采用伪解析方法在计算空间导数的同时,对时间二阶近似误差进行了补偿,使得其能够在时间和空间上同时达到Nyquist谱精度,说明了相比于有限差分方法和伪谱法,伪解析方法具有更高的计算精度。

a—有限差分法(FDM); b—伪谱法(PSM); c—伪解析法(PAM)
3.2 复杂BP模型
为检验所提方法对倾角剧变复杂介质的稳定性,截取一段倾角变化范围是-55°~55°的二维BP2007声学TTI介质模型进行测试。该模型规模为17 km×11.25 km,空间网格单元为6.25 m×6.25 m,时间步长为5 ms,总时间采样点为1 600,记录长度为8 s,纵波震源位于(68.5 km,0),采用主频为20 Hz的Ricker子波震源,采用海绵边界条件,接收排列范围是0~17 km,排列深度为0,接收点间距为25 m,共681道接收,模型参数见图7。
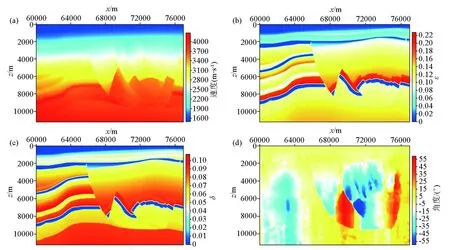
a—纵波速度v0;b—纵波各向异性参数ε;c—变异系数δ;d—极化角θ
图8为采用二维BP2007模型得到的TTI介质纯qP波4 s时刻波场快照及其地震记录。从波场快照(图8a)可见,地震波场能稳定地传播,说明所提方法能适应倾角剧烈变化的情形,具有较高稳定性;同时,在地震记录(图8b)中,地震记录和波场快照信噪比高,无频散,波场反射信息清楚且丰富,绕射波明显,反映出伪解析法能够通过补偿时间步长上的误差有效地提高计算精度,压制频散。
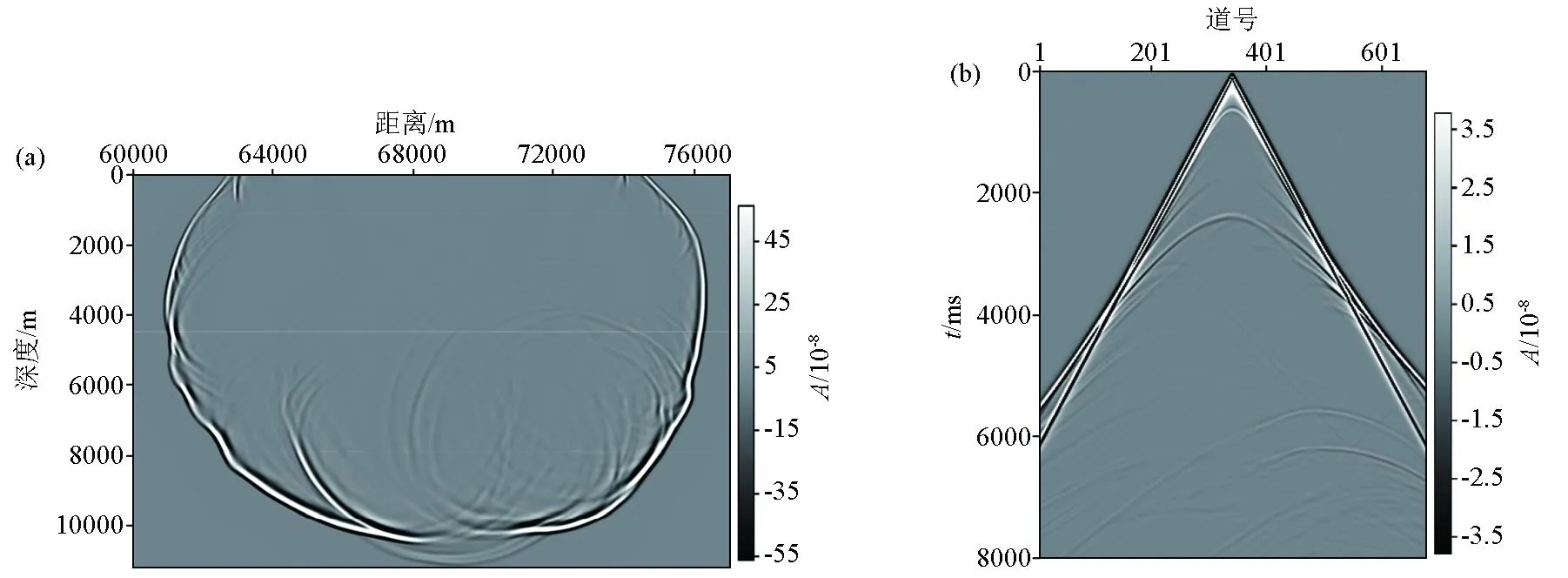
图8 二维BP2007声学TTI介质4 s时刻波场快照(a)及地震记录(b)Fig.8 Two-dimensional BP2007 acoustic TTI medium 4 s time wave field snapshot(a) and seismic record(b)
4 结论
本文在前人的研究基础上,将qP波拟微分方程变换到空间—波数域,并通过坐标变换,推导了时间域TTI介质二阶纯qP波波动方程,引入伪解析算法,实现了基于伪解析法的TTI介质纯qP波地震波场正演模拟。通过多种模型的测试,得出以下认识和结论:
1)克服了拟声波方程的局限性,消除了伪横波干扰,不受模型参数限制且地震波场能稳定传播,具有较为广泛的应用前景;
2)与其他方法相比(有限差分法及伪谱法),伪解析法能有效提高数值模拟精度;
3)简单及复杂模型测试验证了本文方法的正确性与适用性,能够适应复杂介质,且具有更高的计算精度。
