边缘特征和深度加权约束的重力三维相关成像反演

安国强,鲁宝亮,2,3,高新宇,朱武,3,4,李柏森

(1.长安大学 地质工程与测绘学院,陕西 西安 710054; 2海洋油气勘探国家工程研究中心,北京100028; 3长安大学 西部矿产资源与地质工程教育部重点实验室,陕西 西安 710054;4自然资源部 生态地质与灾害防控重点实验室,陕西 西安 710054)

0 引言

相关成像是一种利用相关系数定性解释地质体空间位置和形态的快速成像方法, 相比于常规重力异常反演方法, 其不需要求解大型方程组, 便能够快速提供异常体的平面位置、深度信息等。相关成像法最初是由Patella[1]提出, 用于自然电位测量数据进行地质目标体的三维成像与解释; Mauriello等[2-3]分别将该方法推广到了大地电磁领域和重磁领域; 此后相关成像方法被广泛应用于地球物理数据处理中[4-6]。从相关成像的原理出发, 郭良辉等[7-9]提出了重力、重力梯度数据三维相关成像方法以及磁异常的三维相关成像方法; 侯振隆等[10]提出基于泰勒级数的相关成像方法, 提高了成像速度。为了得到真实的物性参数, 孟小红等[11]和闫浩飞等[12]提出了迭代计算, 反演出了地质体的重磁物性参数。针对直接相关成像结果中出现深部发散的问题, 众多学者提出了不同的改进方法, 主要包括基于异常分离的相关成像[13], 重磁异常垂直梯度三维相关成像[14-15], 重力数据与重力梯度数据的联合相关成像[13,16-17], 基于窗口数据的相关成像[18], 基于深度加权的相关成像[16,19]。然而, 目前重力异常相关成像仍然存在横向分辨率低、深度加权函数超参数过多的问题。

在前人的研究基础上, 本文提出了基于边缘特征和深度加权约束的重力三维相关成像反演方法, 该方法较好地克服了相关成像横向分辨率不高以及深部发散的问题。根据重力相关成像的基本原理, 利用垂向导数(VDR, vertical derivative)和解析信号振幅(ASM, analytical signal amplitude)的边界均衡方法, 得到了异常体深部的水平边缘特征信息, 并提出了利用重力异常水平边缘特征: 均衡垂向导数和均衡解析信号振幅来改善重力异常相关成像横向分辨率的方法; 针对深度加权函数超参数过多的问题,提出了利用一种更为简洁的深度加权函数来改善重力异常相关成像纵向分辨率的方法。最后通过模型试验以及对澳大利亚Olympic Dam多金属矿区实际资料的计算, 证明了约束后的相关成像在横向分辨率和纵向分辨率方面得到了显著的提高, 验证了该方法的正确性和有效性。

1 方法原理

1.1 重力数据相关成像

重力相关成像是通过计算地下某质量点在地面产生的重力异常与实测重力异常之间的归一化互相关系数, 用以表示该质量点是异常源的概率大小。将地下待成像的空间剖分成均匀网格, 然后从地下浅层到深层计算所有网格节点的相关系数从而可以得到整个测区深度范围内各个位置的概率分布。其结果能显示出地下异常地质体的位置和视密度的相对大小[7,13]。

首先将地下成像空间剖分为均匀网格, 并将单个网格视为点质量, 则根据式(1)可以计算地下某一网格q(xq,yq,zq)在地面上任意点(x,y,z)处产生的重力异常:

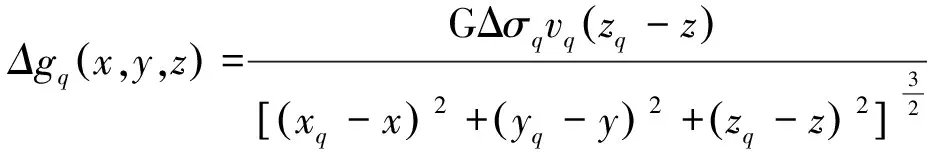
(1)

其中:G为万有引力常数;Δσ为剩余密度;v是网格的体积。

定义测区重力异常与第q点质量重力异常的归一化互相关系数为式(2):

(2)

将式(1)代入式(2), 假设剩余密度为正, 可以约掉G、Δσ、v得到实测异常值Δg与质量基函数B的互相关系数计算式(3):

(3)

式(3)中:

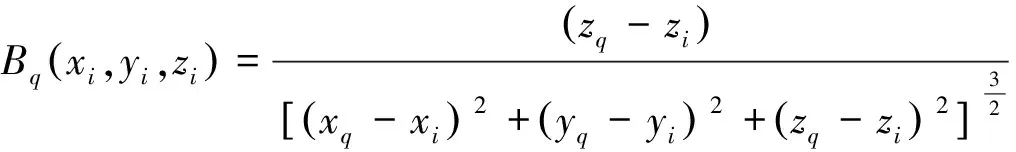
(4)

相关系数Cq的取值范围在-1和1之间, 其绝对值越大, 表明地表的异常是由该质量点产生的概率越大。Cq值越接近于1, 表明该点质量剩余的可能性越大; 反之Cq值越接近于-1, 表明该点质量亏损的可能性越大[7,11]。

1.2 深度加权约束

重力数据相关成像的结果在深部非常发散, 成像的位置与异常体实际的位置之间的误差较大, 即深度方向上的分辨率较低, 故需要引入深度加权函数来提高重力数据相关成像的纵向分辨率[16,19]。在重力三维密度正则化反演中常用深度加权函数提升纵向反演分辨率, Li等[20]、Commer等[21]提出了不同形式的深度加权函数, Li等[20]提出的表达式为:

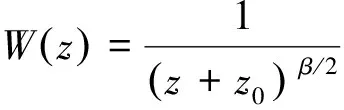
(5)

式中:z0是与异常体深度有关的常数;β是一个正数, 对于重力数据β=2;对于重力梯度数据β=3。 取z0=5,β=2时, 其函数图像如图1所示, 从图中可以看出, 其权重的大小随着深度的增加迅速减小, 在目标异常体的深度位置并没有较高的权重; 而本文对于深度加权函数的需求是在目标深度范围内具有较大权重, 其他深度范围具有较小权重, 故它不适用于解决相关成像在纵向上存在的分辨率低以及深度发散的问题。

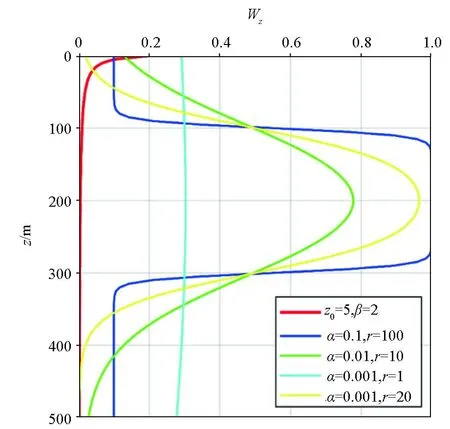
(z1=100m,z2=300m,zmax=500m)

Commer等[21]提出的空间梯度加权函数通过引入先验信息来提高相关成像的分辨率, 其中z方向分量可以作为相关成像的深度加权函数使用[16,19],其表达式为:

(6)

式中:zmax为研究区域地下空间范围内的最大深度;α为经验值, 决定近地表处的权值, 为克服趋肤效应,一般取α=0.001;z1为模型顶部深度,z2为模型底部深度, 二者的取值应由研究区域的地质资料等先验信息决定;r为缩放因子。该式与α、z1、z2、zmax、r这5个参数有关性且形式较为复杂。当先验深度z1=100 m,z2=300 m,zmax=500 m,α分别取0.1、0.01、0.001,r分别取100、10、1、20时, 深度加权函数对于目标深度的加权效果差异很大(图1)。

为了减少超参数对深度加权的影响, 本文提出了一种更简洁的深度加权函数, 其表达式为:

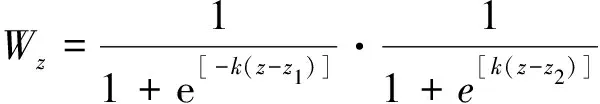
(7)

该函数仅与z1,z2,k这3个参数有关。当先验信息z1=100 m,z2=300 m,k分别取值为0.05、0.10、0.20、0.50时, 其函数图像如图2所示, 可见k的值越小, 函数值随深度变化速率越慢,z1和z2之间的权重逐渐降低;k的值越大, 函数值随深度变化速率越快,z1和z2之间的权重逐渐增大, 图像越接近方波, 函数的光滑度降低。为了使深度加权函数更加光滑, 则k的值应越小; 为了保证z1和z2之间的权重更大, 则k的值应越大; 因此,k的取值应兼顾深度加权函数的光滑性和高权重性, 可通过分析其函数图像, 选取适当的值。例如通过分析图2中不同k值的函数图像, 建议k的取值范围为(0.1±0.05)时, 可以看出在先验深度z1和z2之间具有更大权重, 而且此时函数图像也较为光滑。

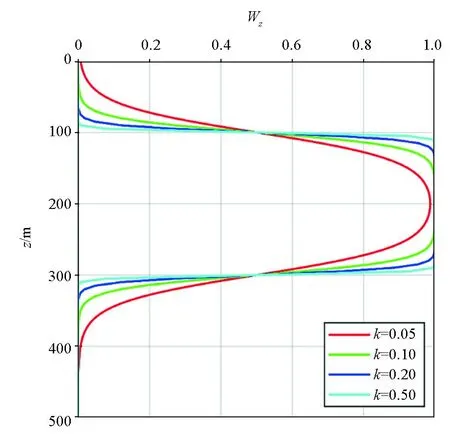
(z1=100m,z2=300m)

将上述深度加权函数应用于相关成像, 则深度加权后的相关系数可表示为:

CD=C·Wz,

(8)

式中:CD为深度加权后的相关系数;C为未加权的相关系数;Wz为深度加权函数。

1.3 边缘特征约束

重力数据相关成像的结果在深度方向上通过引入深度加权函数可以提高成像的纵向分辨率, 然而在水平方向上存在多个异常体时, 重力数据相关成像无法准确地划分出异常体边界。本文通过引入边缘特征信息来改善重力数据相关成像的横向分辨率。边缘特征信息一般通过垂向导数(VDR)或解析信号振幅(ASM)获得。然而, 这类方法对于深部异常体的边界识别结果较为模糊。因此, 通过反正切函数将边缘特征的强、弱异常信号进行均衡放大, 实现深部边界识别。本文选择均衡垂向导数(VDR)和解析信号振幅(ASM)作为水平加权函数, 对比研究它们对重力数据相关成像横向分辨率的改善效果。

反正切函数的边界均衡识别方法, 其计算公式为:

Bf(x,y,z0)=arctan[R·f(x,y,z0)],

(9)

式中:R是均衡系数, 用来调节强、弱信号均衡放大的程度。如图3所示,从R分别取1、5、50、100时的函数图像可以看出,随着R的增大函数变化的斜率增大, 对于0值附近的值的放大程度也越大, 即可实现对于强、弱信号的均衡放大。将垂向导数和解析信号振幅边缘识别方法对相关成像进行水平加权, 则要求在识别的异常体位置区域具有较高的权重, 在非边缘位置区域的权重迅速减小为0, 从而达到增强边界信息的作用。

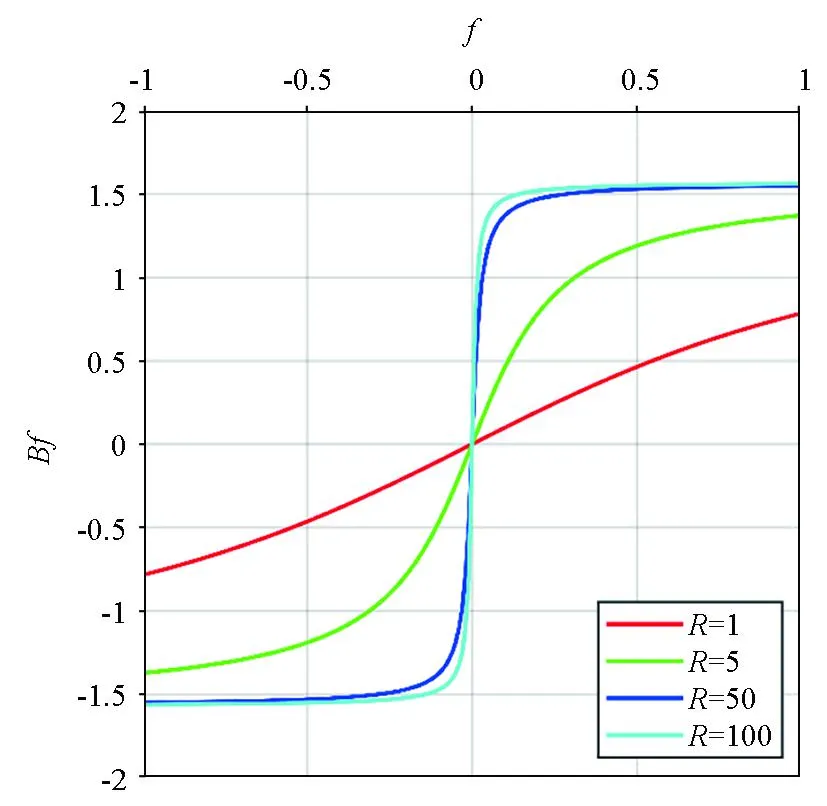
图3 不同均衡系数的反正切均衡函数Fig.3 Arctangent balance functions with different balance coefficients

垂向导数(VDR)方法最初由Hood等[22]和Bhattacharyya[23]提出, 该方法利用零值位置来识别地质体的边缘位置。将均衡垂向导数(取绝对值)归一化后应用于重力数据相关成像水平加权, 其计算公式为式(10)。

解析信号振幅(ASM)又称总梯度模量, 由Nabighian[24-25]提出, 该方法利用极大值位置来识别地质体的边缘位置。将均衡解析信号振幅归一化后应用于重力数据相关成像水平加权, 其计算公式为式(11)。

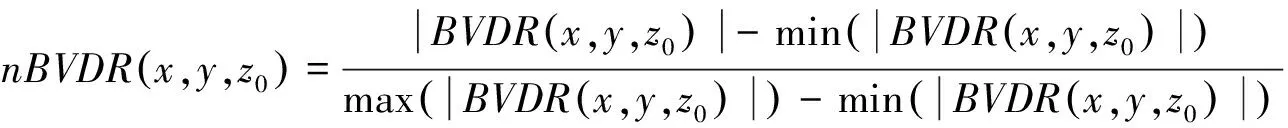
(10)

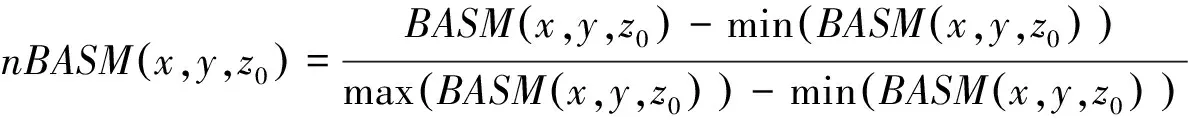
(11)

式中:x,y分别是观测点坐标;z0是观测面的高度。

本文对重力数据相关成像的加权处理可统一写为:

CGT=C·Wz·Wh,

(12)

式中:CGT为总加权相关系数;C为未加权相关系数;Wz为深度加权函数;Wh为水平加权函数,Wh可以为nBVDR或nBASM。

2 理论模型试验

2.1 含5%噪声试验

设置两个剩余密度、大小相同的直立长方体模型, 模型参数如表1所示; 平面测网在x、y方向为0～1 000 m, 点距为10 m, 高度位于0 m; 成像范围为0～500 m。 如图4所示, 该模型的重力异常(图4a)含5%高斯白噪声, 计算出该模型的归一化均衡垂向导数(图4b)和归一化均衡解析信号振幅(图4c) , 其中均衡系数R=10.0。

表1 模型参数(含5%噪声)Table 1 Model parameters (including 5% noise)

a—重力异常;b—归一化均衡垂向导数(nBVDR);c—归一化均衡解析信号振幅(nBASM)

使用Commer等[21]提出的空间梯度加权函数对相关成像进行深度加权。空间梯度加权函数的先验深度信息z1=100 m,z2=300 m, 取zmax=500 m,α=0.001,r=50; 其相关成像深度加权的三维结果如图5a所示,y=500 m处的垂向切片如图5b所示,z=200 m处的水平切片如图5c所示。 从图中可以看出, Commer等[21]提出的空间梯度加权函数使成像位置集中在模型的先验深度范围内, 提高了相关成像的纵向分辨率; 但在水平方向上, 两个异常体之间的边界位置无法区分, 横向分辨率很低。

a—深度加权约束的成像结果;b—y=500 m的垂向切片(深度加权约束);c—z=200 m的水平切片(深度加权约束);d—本文方法成像结果(Wz+VDR加权);e—y=500 m的垂向切片(Wz+VDR加权);f—z=200 m的水平切片(Wz+VDR加权);g—本文方法成像结果(Wz+ASM加权);h—y=500 m的垂向切片(Wz+ASM加权);i—z=200 m的水平切片(Wz+ASM加权)

使用本文提出的基于边缘特征与深度加权约束的重力相关成像反演方法的三维结果如图5d、g所示,y=500 m处的垂向切片如图5e、h所示,z=200 m处的水平切片如图5f、i所示。 其中纵向约束使用本文提出的深度加权函数, 先验信息上底z1取100 m, 下底z2取300 m, 调节因子k=0.1。 横向约束分别使用归一化均衡垂向导数和归一化均衡解析信号振幅。 从图中可以看出, 在本文提出的深度加权函数的基础上, 使用归一化均衡垂向导数和归一化均衡解析信号振幅的边缘特征信息均使相关成像的横向分辨率显著提高; 其中, 使用归一化均衡垂向导数的横向分辨率更高。 基于文章篇幅的原因, 本文就不再展示该模型不含噪声的试验。通过对比可知含5%噪声的结果与不含噪声的结果基本相同, 表明相关成像的方法具有良好的抗噪性, 故后文不再展示其他含噪试验结果。

2.2 复杂直立模型试验

为了研究不同剩余密度成像的效果, 设置了不同剩余密度直立长方体的组合模型; 平面测网在x、y方向为0～1 000 m, 点距为10 m, 高度位于0 m, 成像范围为0～500 m。模型参数如表2所示。该模型的重力异常为图6a, 计算出该模型的归一化均衡垂向导数(图6b)和归一化均衡解析信号振幅(图6c), 其中均衡系数R=2.0。

表2 复杂直立模型参数Table 2 Complex upright model parameters

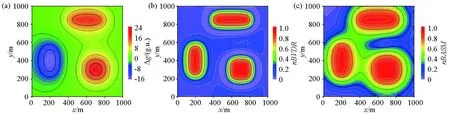
a—重力异常;b—归一化均衡垂向导数(nBVDR);c—归一化均衡解析信号振幅(nBASM)

使用Commer等[21]提出的空间梯度加权函数对相关成像进行深度加权。先验深度信息z1=50 m,z2=300 m, 取zmax=500 m,α=0.001,r=50; 其相关成像深度加权的三维结果如图7a所示, 在水平方向上, 剩余密度为一正一负的异常体之间的边界位置可以区分, 但剩余密度都为正的异常体之间的边界位置无法区分, 横向分辨率很低。

a—深度加权约束的成像结果;b—y=300 m的垂向切片(深度加权约束);c—z=200 m的水平切片(深度加权约束);d—本文方法成像结果(Wz+VDR加权);e—y=300 m的垂向切片(Wz+VDR加权);f—z=200 m的水平切片(Wz+VDR加权);g—本文方法成像结果(Wz+ASM加权);h—y=300 m的垂向切片(Wz+ASM加权);i—z=200 m的水平切片(Wz+ASM加权)

使用本文方法的三维结果如图7所示, 纵向约束所需先验信息上底z1取50 m, 下底z2取300 m, 调节因子k=0.1。横向约束分别使用归一化均衡垂向导数和归一化均衡解析信号振幅。经过加权后成像的纵向分辨率和横向分辨率显著提高; 其中, 使用归一化均衡垂向导数比归一化均衡解析信号振幅的纵向分辨率更高。

2.3 复杂倾斜模型试验

为了验证更为复杂的情况, 设置了不同剩余密度倾斜长方体和台阶的组合模型; 平面测网在x、y方向为0～1 000 m, 点距为10 m, 高度位于0 m, 成像范围为0～500 m。模型参数如表3所示。该模型的重力异常为图8a, 计算出该模型的归一化均衡垂向导数(图8b)和归一化均衡解析信号振幅(图8c), 其中均衡系数R=10.0。

表3 复杂倾斜模型参数Table 3 Complex tilt model parameters

a—重力异常;b—归一化均衡垂向导数(nBVDR);c—归一化均衡解析信号振幅(nBASM)

使用Commer等[21]提出的空间梯度加权函数对相关成像进行深度加权三维结果如图9a所示。先验深度信息z1=99 m,z2=430 m, 取zmax=500 m,α=0.001,r=50; 同样在水平方向上, 剩余密度为一正一负的异常体之间的边界位置可以区分, 但剩余密度都为正的异常体之间的边界位置无法区分, 横向分辨率也很低。使用本文方法的三维结果如图9所示, 纵向约束所需先验信息上底z1取99 m,下底z2取430 m, 调节因子k=0.1。横向约束分别使用归一化均衡垂向导数和归一化均衡解析信号振幅。经过加权后成像的纵向分辨率和横向分辨率显著提高。

a—深度加权约束的成像结果;b—y=250 m的垂向切片(深度加权约束);c—z=250 m的水平切片(深度加权约束);d—本文方法成像结果(Wz+VDR加权);e—y=250 m的垂向切片(Wz+VDR加权);f—z=250 m的水平切片(Wz+VDR加权);g—本文方法成像结果(Wz+ASM加权);h—y=250 m的垂向切片(Wz+ASM加权);i—z=250 m的水平切片(Wz+ASM加权)

通过上述模型试验可以发现, 使用本文提出的深度加权函数对相关成像在深度方向加权, 使成像的结果在深部更加收敛, 且使成像的位置集中在所给的先验深度范围内, 使相关成像的纵向分辨率显著提高; 但深度加权函数受先验深度信息z1、z2的影响较大, 故先验深度信息的选取对成像结果至关重要。

由于均衡垂向导数和均衡解析信号振幅的边缘特征方法可以增强对于异常体深部位置的识别, 故本文在水平方向上分别使用均衡垂向导数和均衡解析信号振幅对相关成像进行水平加权, 均使相关成像的横向分辨率显著提高; 其中, 使用均衡垂向导数加权的效果更好。

3 实际资料处理

澳大利亚的Olympic Dam (Cu-U-Au-Ag)金属矿床是南澳大利亚太古宙元古代高勒克拉通边缘的几种氧化铁—铜—金—铀(IOCG-U)矿床中最大的矿床[26-27], 矿床位于高勒前寒武纪克拉通东部, 基底构造层为广阔的隆起区, 区域岩石由区域变质岩、条带状磁铁石英岩和花岗岩组成。矿床被深而狭窄的地堑沉积不整合覆盖, 地堑由快速沉积的角砾岩、火山碎屑岩和长英质火山岩充填, 其上又被新元古代砂砾岩和寒武纪石灰岩层所覆盖。角砾岩的主要成分是花岗岩碎块和各种类型的赤铁矿。矿床中主要的硫化矿物有黄铜矿、斑铜矿和辉铜矿。品位较高的矿带由浸染状辉铜矿和斑铜矿组成, 产于矿床较高部位。铀品位较高的地区, 通常含有细脉和细粒浸染状沥青铀矿。金和银品位虽低,但与铜和铀共生,因而具有经济价值。在个别金矿化的地区, 稀土元素含量甚高[28-30]。

IOCG型矿床,即铁氧化物—铜—金矿床, 指铁氧化物含量大于20%的铜—金矿床, 其一般具有规模大、品位高、元素多、埋藏浅、易采选等特点[31-32]。由于IOCG型矿床富含铁氧化物且蚀变范围广阔, 地球物理特征明显, 尤其是重磁力特征[33], 因此,高精度的重磁勘探是寻找IOCG矿床重要的有效手段之一。由于Olympic Dam多金属矿床受到含铁氧化物的影响,产生大量的磁铁矿、赤铁矿或半生矿物,这些组合物中铁氧化物具有不同的磁性,导致Olympic Dam多金属矿床的磁性特征变化较大,该变化也伴随较为显著的密度变化和重力变化,伴随铁氧化物蚀变产生明显的重力异常高[34]。

图10显示了高勒—克拉顿省的地质结构[35]。在高勒—克拉顿省的东段, 以黑色矩形标记的Olympic Dam多金属矿区作为研究区域。图11显示了Olympic Dam多金属矿床的地质示意图[36]。图12显示了该区域的4口钻井的岩心实测密度曲线。钻井岩心实测密度曲线及地质剖面图显示高密度岩体主要分布集中在400～1 400 m范围内。

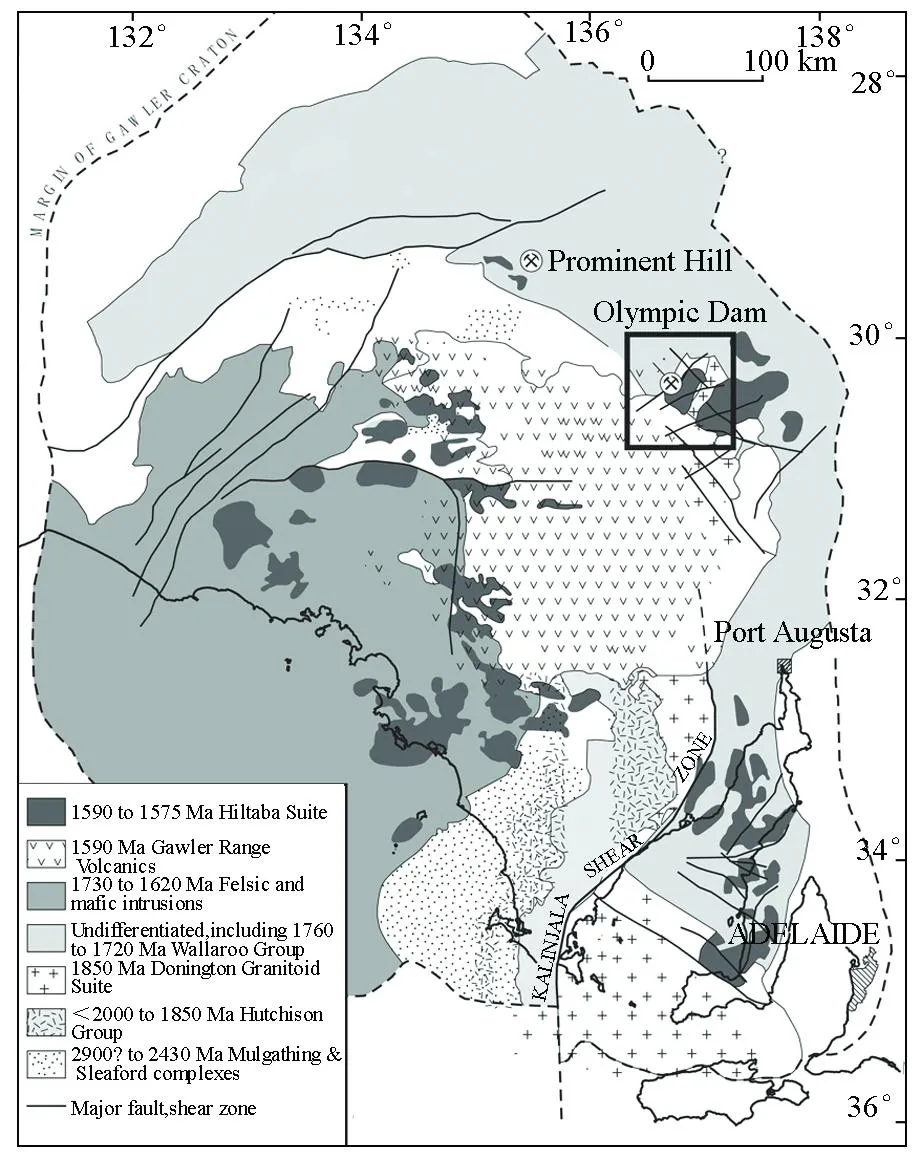
图10 高勒克拉顿省的基底地质图[35]Fig.10 Basement geological map of the Gawler Craton Province [35]

图11 超巨型Olympic Dam角砾岩群的简化地质图及剖面[36]Fig.11 Simplified geological map and cross-sectional subsurface structure of the supergiant Olympic Dam breccia complex [36]

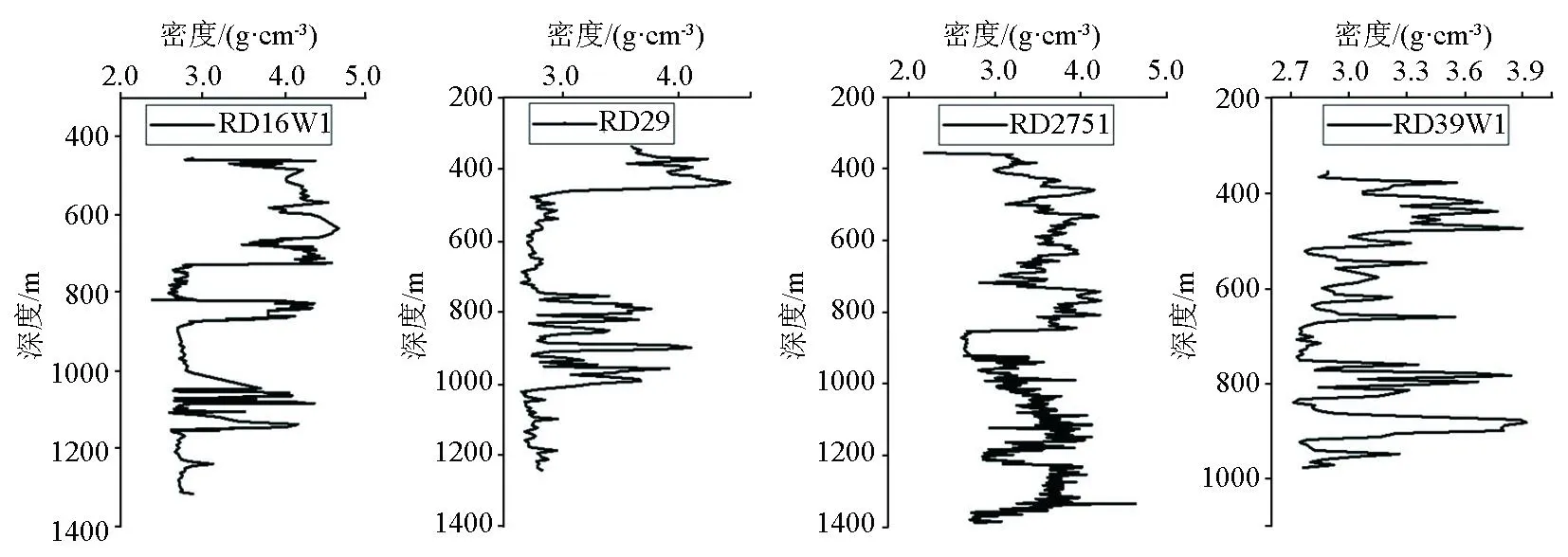
图12 钻井岩心实测密度曲线Fig.12 Drill core measured density curve

为了获得矿体引起的剩余重力异常, 使用二维小波多尺度分解方法[37]对该区域的布格重力异常数据进行异常的分离, 如图13a所示为重力异常的观测值, 图13b为区域重力异常, 图13c为剩余重力异常。对其剩余重力异常计算其归一化均衡垂向导数和归一化均衡解析信号振幅, 其中均衡系数R=2.0。

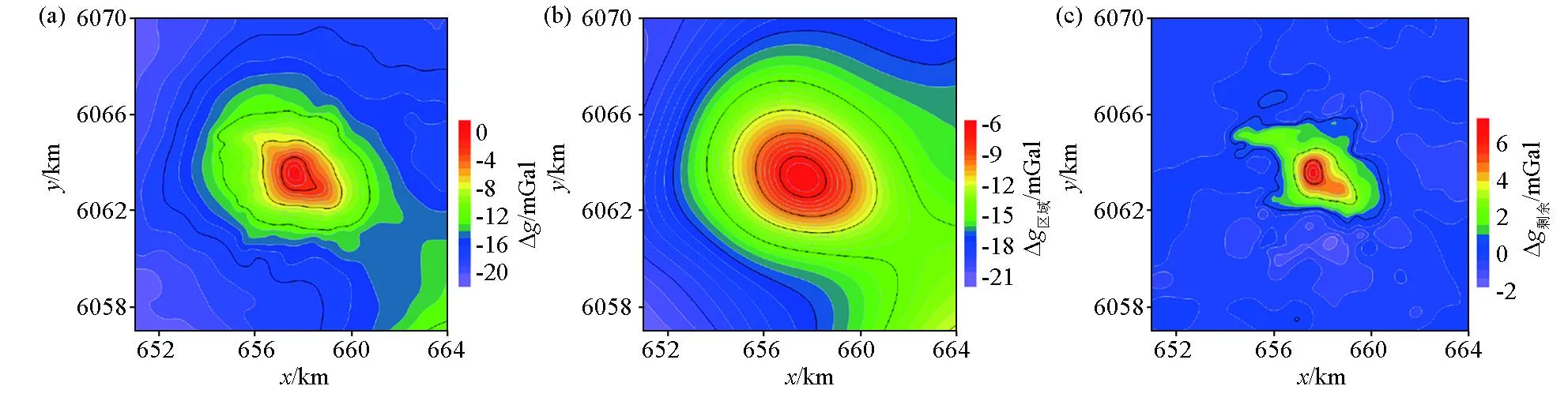
a—重力异常观测值;b—区域重力异常;c—剩余重力异常

使用剩余重力异常数据进行相关成像, 由钻井资料可知该高密度体的先验深度信息大约在400～1 400 m。故在使用深度加权函数进行纵向约束时, 先验信息z1=400 m,z2=1 400 m, 调节因子k=0.01。再分别使用归一化均衡垂向导数和归一化均衡解析信号振幅进行水平加权, 相关成像加权结果的三维图、y=6 063.5 km处的垂向切片、z=750 m处的水平切片如图14所示。成像结果的水平位置与5%Fe含量等值线基本一致, 深度位置集中在400～1 400 m范围内; 其中均衡垂向导数比均衡解析信号振幅加权的分辨率更高; 本文方法成像的结果与前人反演的结果类似[38-39], 较好地反映了目标岩体的位置。

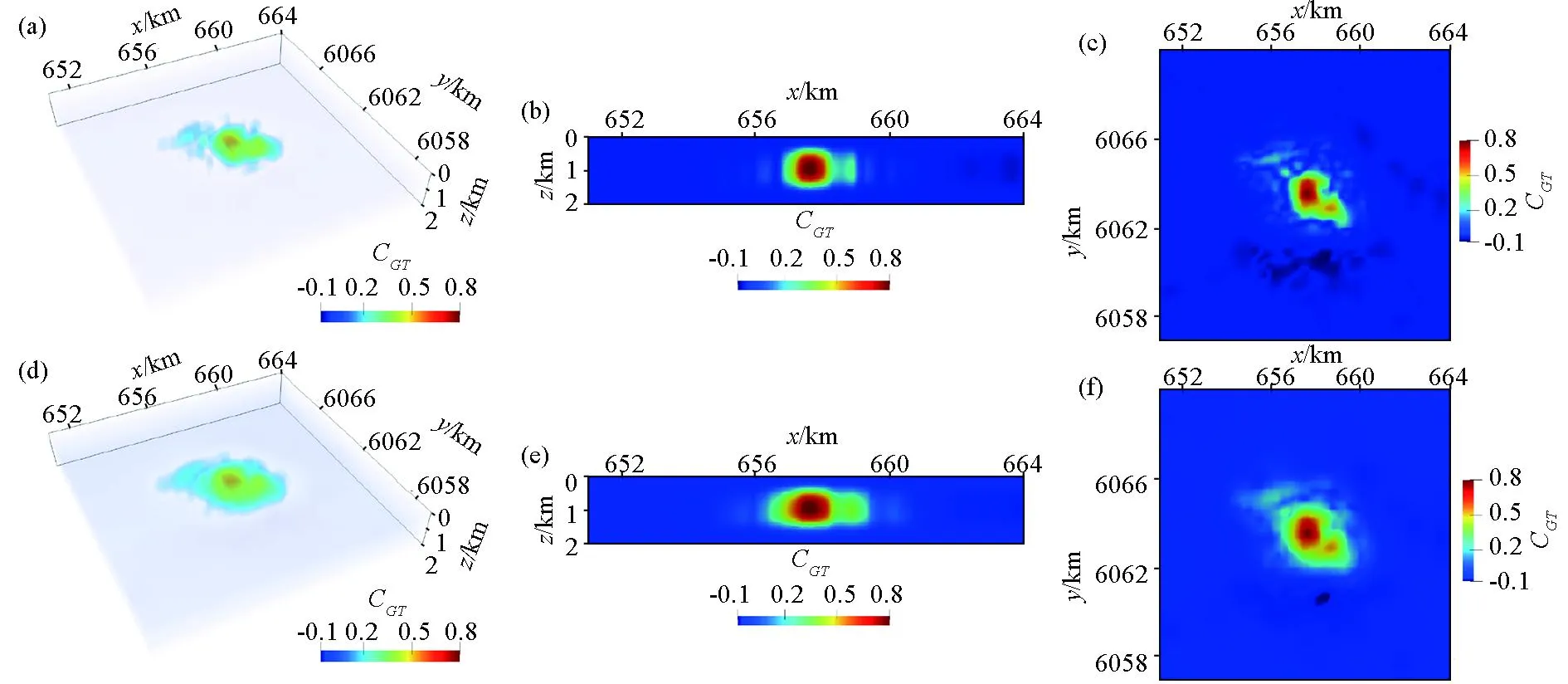
a—本文方法成像结果(Wz+VDR加权);b—y=6 063.5 km的垂向切片(Wz+VDR加权);c—z=750 m的水平切片(Wz+VDR加权);d—本文方法成像结果(Wz+ASM加权);e—y=6 063.5 km的垂向切片(Wz+ASM加权);f—z=750 m的水平切片(Wz+ASM加权)

4 结论

针对重力异常相关成像的结果存在深部发散、深度加权函数参数过多以及由于多个异常体的重力异常叠加导致相关成像横向分辨率和纵向分辨率低的问题。本文提出了基于边缘特征和深度加权约束的重力三维相关成像反演方法, 该方法引入了重力异常均衡垂向导数以及均衡解析信号振幅, 并且提出了一种更为简洁的深度加权函数, 较好地改善了重力异常相关成像的横向和纵向分辨率。通过模型试验以及对澳大利亚Olympic Dam多金属矿区实测重力资料的处理, 得到了如下结论:

1) 使用反正切函数对重力异常垂向导数和解析信号振幅识别的边界进行均衡, 可以得到异常体深部的边缘特征。将均衡垂向导数和均衡解析信号振幅作为重力相关成像的水平加权, 可以在横向上明显地区分出异常体的边界位置, 提高了重力异常相关成像的横向分辨率。

2) 本文提出的深度加权函数除了先验深度信息z1和z2, 只与因子k有关, 需要给定的参数数量很少, 减少了超参数的选取对于深度加权的影响。通过给定先验深度信息z1和z2有效地改善了相关成像深部发散的问题, 提高了重力异常相关成像的纵向分辨率。然而深度加权函数非常依赖先验深度信息z1和z2, 可通过钻井等其他地球物理资料得到较为准确的先验深度信息, 从而获得较好的深度加权相关成像结果。

3) 本文方法更适用于直立块状异常体的三维成像, 对于倾斜板状异常体的成像效果有限。

4) 作为一种半定量的解释方法, 后续可为三维密度反演提供初始模型。

致谢：感谢南澳大利亚资源信息网站提供的Olympic Dam多金属矿区布格重力数据。