基于全局自适应MCMC算法的裂缝型储层缝隙流体因子叠前地震反演

张婧,汪勇 ,赵慧言,衡德 ,黄君,张晓丹,王文文 ,贺燕冰

(1. 四川长宁天然气开发有限责任公司,四川 成都 610000; 2. 成都捷科思石油天然气技术发展有限公司,四川 成都 610000)

0 引言

裂缝型储层是非常规油气勘探开发的重要对象,含裂缝储层以及缝隙流体反演也已成为研究的重点。准确高效识别含裂缝储层的缝隙流体并评估其反演不确定性具有重要应用价值,对非常规油气勘探开发提供一定指示作用。

对于含裂缝储层流体识别,其关键是构建一个合理且敏感的流体指示因子。对于各向同性岩石,基于Gassmann[1]的孔隙弹性理论,从地震数据直接估算各种流体敏感参数已实现含油气储层流体识别。其中Russell等[2-3]提出了基于纵波阻抗与横波阻抗差值的流体因子,业界将其定义为Russell流体因子并广泛应用。Yin等[4]根据一个严格的经验关系式将Russell流体因子解耦并定义了新的流体指示因子。对于各向异性含裂缝岩石,由于地震波对含裂缝岩石中传播方向的依赖性会导致各向异性现象,含裂缝储层表现出的较强各向异性引起其地震响应对地震波入射角以及方位角的变化更为敏感,提高了各向异性流体因子反演的可行性。Schoenberg和Douma[5]确定了两个裂缝弱度参数的比值为流体指示因子,该各向异性流体指示因子已被广泛应用。Shaw和Sen[6]基于垂直裂缝介质假设,实现流体指示因子地震AVOA预测。van der Neut等[7]将储层AVO梯度项与各向异性缝隙流体联系起来,引入了各向异性流体指示因子的反演理论。陈怀震等[8]综合分析了各向同性介质下的流体识别方法,从岩石物理模型出发预测获得各向异性介质流体因子。陈怀震等[9]建立了各向异性的岩石物理模型,并通过岩石物理分析了缝隙流体与储层微观物性参数之间的关系,最终结合AVAZ反演得到了缝隙流体因子。谢春辉等[10]认为利用Ruger提出的各向异性方程反演得到的各向异性梯度参数,与各向同性梯度参数的比值对储层流体敏感并将其定义为流体指示因子。孙炜等[11]在直角坐标系考虑各向异性参数与Russell流体因子的理论,并定义了一种新的流体指示因子。Pan等[12]提出了拟法向弱度以及拟切向弱度的概念,并基于EIVOA反演得到流体模量。印兴耀等[13]弹性参数以及各向异性参数的组合定义了一个各向异性流体因子,并应用五维地震数据实现流体因子的反演。

目前,各向异性参数反演方法主要有确定性反演以及概率化反演两种。确定性反演虽然可以通过各种全局优化算法预测最优反演参数,但难以满足复杂地下介质的综合识别[14]。尤其是随着裂缝介质复杂程度的提高,待反演参数不断增加,增加了地震反演的不稳定性与不确定性,亟需结合概率化反演算法在准确预测模型参数的同时,分析反问题的解的不确定性[15]。统计学反演主要是基于贝叶斯理论获得反演参数的最优解和置信区间,用于参数不确定性分析[16-17]。最大后验概率(MAP)解是统计学反演中最常用的算法,其引入待估计参数的先验分布信息,对最大似然估计解进行了改进,有效地缓解了地震反演的不适定性[18]。然而,MAP解只适用于后验概率密度分布为显式,即后验概率密度分布可以用具体的方程表征的情况,因此很难解决非线性反演问题[19]。与MAP解不同,MCMC算法不仅可以解决非线性反演问题,还适用于隐式解的反演,其应用较为广泛。理论上,MCMC算法可以获得模型参数的全局最优解,但存在的问题是算法启动缓慢,优化过程缓慢,即使得到最优解也会继续搜索,计算效率较低[20]。

本文以线性滑动模型为基础,基于准裂缝法向弱度以及准裂缝切向弱度定义了一个新的缝隙流体指示因子,结合散射理论和Born近似方程推导了包含准裂缝法向弱度以及准裂缝切向弱度的各向异性反射系数方程,应用改进的全局自适应MCMC反演算法实现缝隙流体指示因子叠前地震反演。

1 缝隙流体指示因子预测方法原理

在均匀各向同性背景夹杂一组对称轴为水平方向的裂缝可看作等效HTI(horizontal transversely isotropy)介质。基于线性滑动理论模型[21],HTI刚度系数矩阵可表示为:

(1)

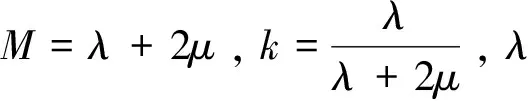
(2)

Schoenberg 和 Sayers认为KN/KT能够被当作缝隙流体指示因子,KN和KT表示裂缝柔度参数,二者与裂缝法向弱度以及切向弱度之间的关系式可以表示为

(3)

根据方程(2)和方程(3),并参照Schoenberg 和 Sayers的理论,定义新的缝隙流体指示因子为:

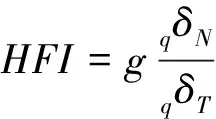
(4)

式中:g表示剪切模量与纵波模量的比值。基于散射理论以及波恩近似方程[22],任意对称的各向异性介质的入射P波反射系数方程Rpp可以写成一个散射函数S方程的形式:

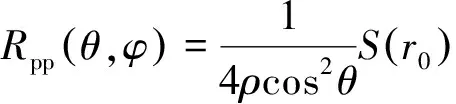
(5)

式中:θ是P波的入射角,φ是方位角。散射函数S可以表达为:

S(r0)=Δρcos2θ+ΔCη,

(6)

式中:Δρ代表在弹性界面上的密度的扰动量,ΔC表示刚度矩阵的扰动量,可由方程(1)中的CHTI计算得到,η矩阵的各分量可表示为:

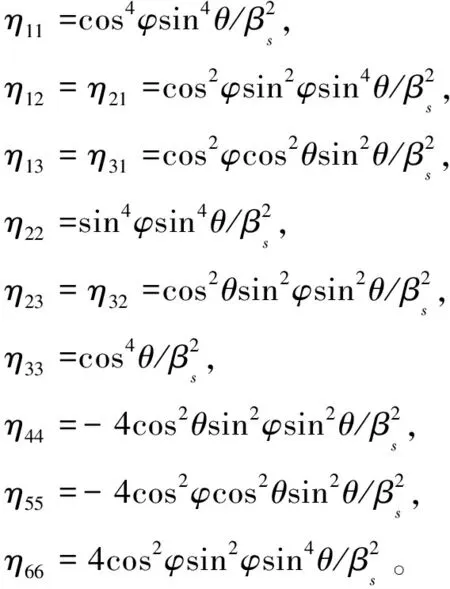
(7)

将方程(1),方程(2),方程(4),方程(6),方程(7)代入方程(5)即可得到缝隙流体指示因子各向异性反射系数方程具体表达形式:

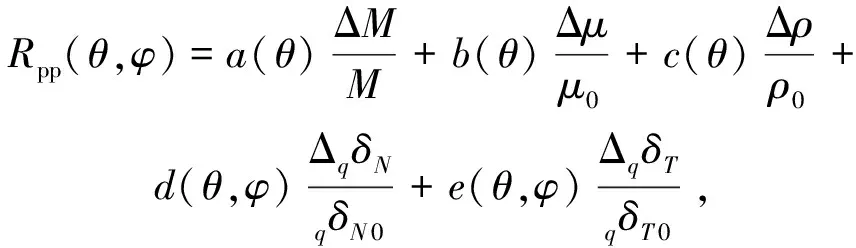
(8)

式中:

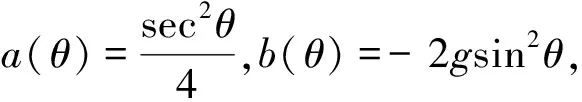
为验证推导的反射系数方程,我们设计了一个理论双层模型,模型参数如表1所示,并将本文推导的近似方程与P-K[23]方程进行对比,如图1所示。从图1中可以看出,入射角在0°～30°范围内,近似方程与P-K方程吻合程度高,满足反演的精度要求。

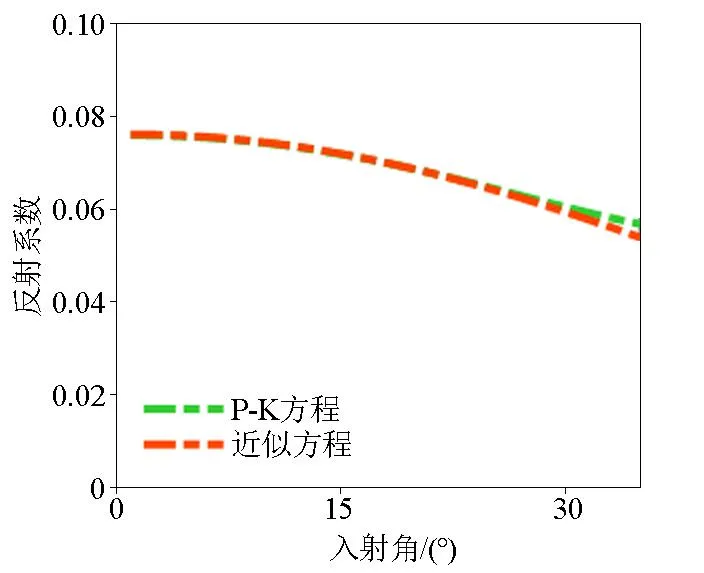
图1 反射系数方程对比Fig.1 Reflection coefficient equation comparison

表1 双层模型参数Table 1 Parameters of double-layer model

2 缝隙流体指示因子贝叶斯反演方法

本文的反问题可以写成:

s=f(m)+e

(9)

式中:s代表方位地震数据;f代表连接模型参数与方位地震数据的方程;m表示待反演参数(M,μ,ρ,qδN,qδT);e是随机噪声。

反问题的解由模型参数的后验分布给出,该后验分布与贝叶斯框架下的先验分布和似然函数的乘积成正比。后验分布可表示为

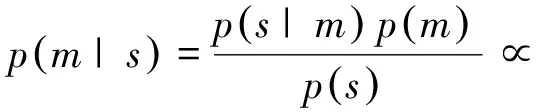
(10)

在本研究中,我们假设噪声满足高斯分布,似然函数可表示为

(11)

待反演参数的先验信息,可从测井资料、岩心资料和其他地质资料中获得[24]。本文假设待反演的五个参数满足高斯分布,参数之间相互独立,因此先验函数可表示为

(12)

为了降低随机模拟过程的计算复杂度,对后验分布的两侧进行对数运算。待反演参数的后验分布可表示为[25-26]

(13)

基于统计学经典的贝叶斯理论,本文在一般的MCMC反演算法的基础上引入全局自适应Metropolis算法,全局自适应策略的目的是用所有已经接受的建议修改提议分布,实现全局最优解的寻找与判别。改进的全局自适应MCMC反演算法总结如下:

我们假设总迭代次数I, 非自适应阶段n0和模型参数l。不适应阶段是指迭代开始时参数尚未收敛的时期。当i≤n0时,建议分布的严格正定的协方差矩阵等于由先验信息定义的初始协方差矩阵。当i>n0时,根据全局自适应策略可从采样的样本点计算协方差矩阵,如式(15)所示:

(14)

假设马尔可夫链在第i次迭代时的更新状态为li,li+1从高斯建议分布中采样:

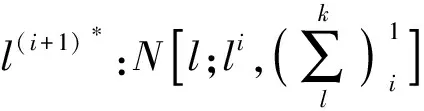
(15)

接受概率由Metropolis-Hasting算法给出:

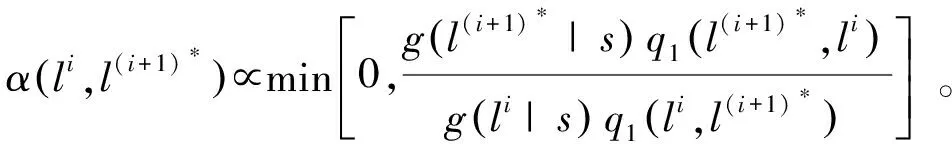
(16)

一般来说,马尔可夫链的收敛效率取决于建议分布与目标分布的匹配程度。相较于一般的MCMC反演算法采用固定的提议分布,全局自适应策略能够根据已生成的样本点有效调整建议分布,使其能够有效拟合到目标分布,以得到全局最优解。

图2,图3,图4分别展示了不同信噪比情况下的纵波模量、剪切模量、密度、准裂缝法向弱度、准裂缝切向弱度以及流体指示因子HFI的反演结果。图2是无噪情况下5个待反演参数的反演结果,其中黑色曲线代表待反演参数的实际测井曲线,红色曲线代表模型参数反演结果。为了验证反演结果的鲁棒性,不断加入高斯噪声,图3,图4分别表示信噪比为5∶1和2∶1时的反演结果。从3个图中我们可以看出,在无噪时纵波模量、剪切模量、准裂缝法向弱度、准裂缝切向弱度以及HFI的反演结果曲线与实际井数据吻合程度较高,均达到了90%以上,密度的反演结果与其他参数相比较差,但也实现了85%的吻合度,我们认为密度参数的反演结果稍差是因为其在上下界面处变化较小,在反射系数方程中贡献度较低,导致了反演结果存在一定偏差。即使信噪比为2∶1时,纵波模量、剪切模量、准裂缝法向弱度、准裂缝切向弱度以及HFI的反演结果与井曲线的误差也能控制在20%以内,这也验证了本文所提出的反演方法的适用性与抗噪性。以缝隙流体因子HFI为例,将HFI参数的收敛过程展示如图5所示,纵坐标是反演结果与井曲线的相关系数,横坐标为迭代次数,可以看出迭代次数为1 300次时,反演结果就已实现收敛。

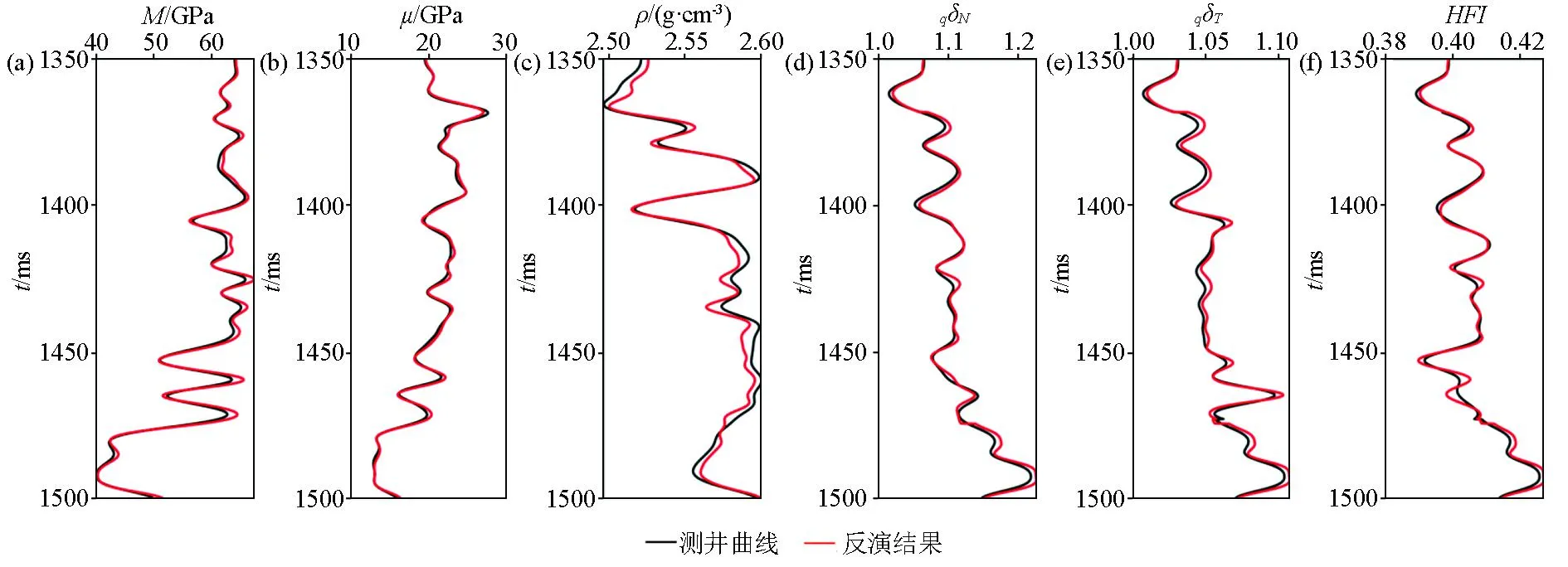
图2 无噪情况下纵波模量(a)、剪切模量(b)、密度(c)、准裂缝法向弱度(d)、准裂缝切向弱度(e)以及流体指示因子HFI(f)的反演结果Fig.2 Inversion results of P-wave modulus(a),shear modulus(b),density(c),normal weakness of quasi-fracture(d),tangential weakness of quasi-fracture(e),and fluid indicator factor HFI(f) without noise

图3 信噪比为5∶1情况下纵波模量(a)、剪切模量(b)、密度(c)、准裂缝法向弱度(d)、准裂缝切向弱度(e)以及流体指示因子HFI(f)的反演结果Fig.3 Inversion results of P-wave modulus(a),shear modulus(b),density(c),normal weakness of quasi-fracture(d),tangential weakness of quasi-fracture(e) and fluid indicator factor HFI(f) when the signal-to-noise ratio is 5∶1

图4 信噪比为2∶1情况下纵波模量(a)、剪切模量(b)、密度(c)、准裂缝法向弱度(d)、准裂缝切向弱度(e)以及流体指示因子HFI(f)的反演结果Fig.4 Inversion results of P-wave modulus(a),shear modulus(b),density(c),normal weakness of quasi-fracture(d),tangential weakness of quasi-fracture(e) and fluid indicator factor HFI(f) when the signal-to-noise ratio is 2∶1

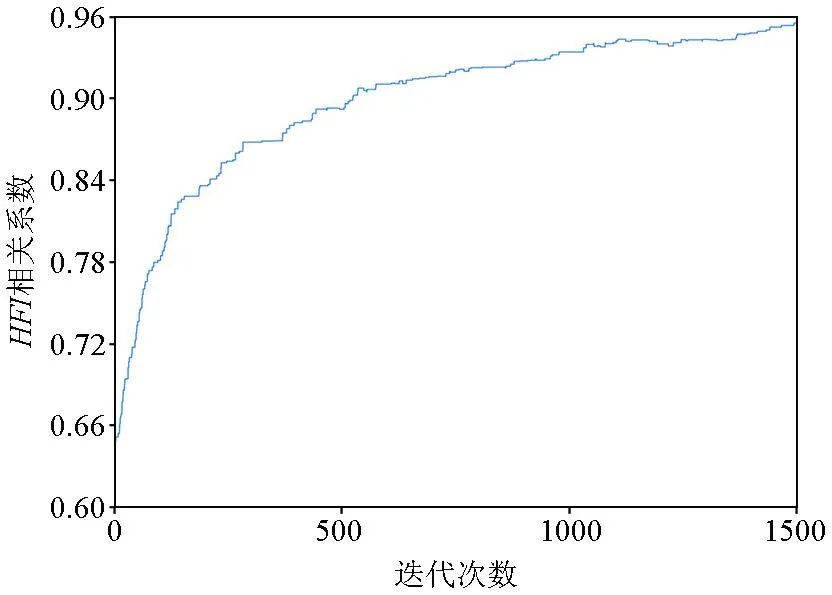
图5 流体指示因子HFI收敛曲线Fig.5 Convergence curve of fluid indicator factor HFI

3 实际资料及应用

选取中国四川盆地某地区的方位地震资料来验证本文所提出的反演方法的实用性。该地区优质页岩分布面积广、成藏条件较好、储层质量好,极具勘探开发前景,且本研究应用的井钻遇油气层。选择不同方位角的叠前地震实测数据进行应用,叠前地震数据在反演前已经过处理,我们假设处理后的地震数据可以忽略层间多次波以及波形转换效应。此外,我们根据井数据计算得到的纵波模量、剪切模量、密度、准裂缝法向弱度、准裂缝切向弱度以及缝隙流体指示因子HFI建立低频模型,作为反演的约束并计算模型参数先验分布的均值以及方差。本文应用的方位地震数据45°以及135°,入射角为6°、18°以及30°,叠加地震剖面如图6所示,其中黑色实线表示井位置,蓝色虚线为目标层段。图7显示了纵波模量、剪切模量、密度、准裂缝法向弱度、准裂缝切向弱度以及缝隙流体指示因子HFI的实际资料反演结果。我们发现,目标层的纵波、剪切体积模量显示出较低的值,准裂缝法向弱度、准裂缝切向弱度以及HFI显示出较高的值,法向和切向裂缝弱度的反演结果表明该层的裂缝发育,HFI的反演结果表明该层裂缝中充填有流体,综合分析后我们可以得到在目的层发育有裂缝,且裂缝内充填有缝隙流体,成像测井解释结果为该目的层发育有大量裂缝,钻井结果表明在目的层钻遇油气层,反演结果与测井解释结果较为符合,验证了反演方法的准确性与适用性。

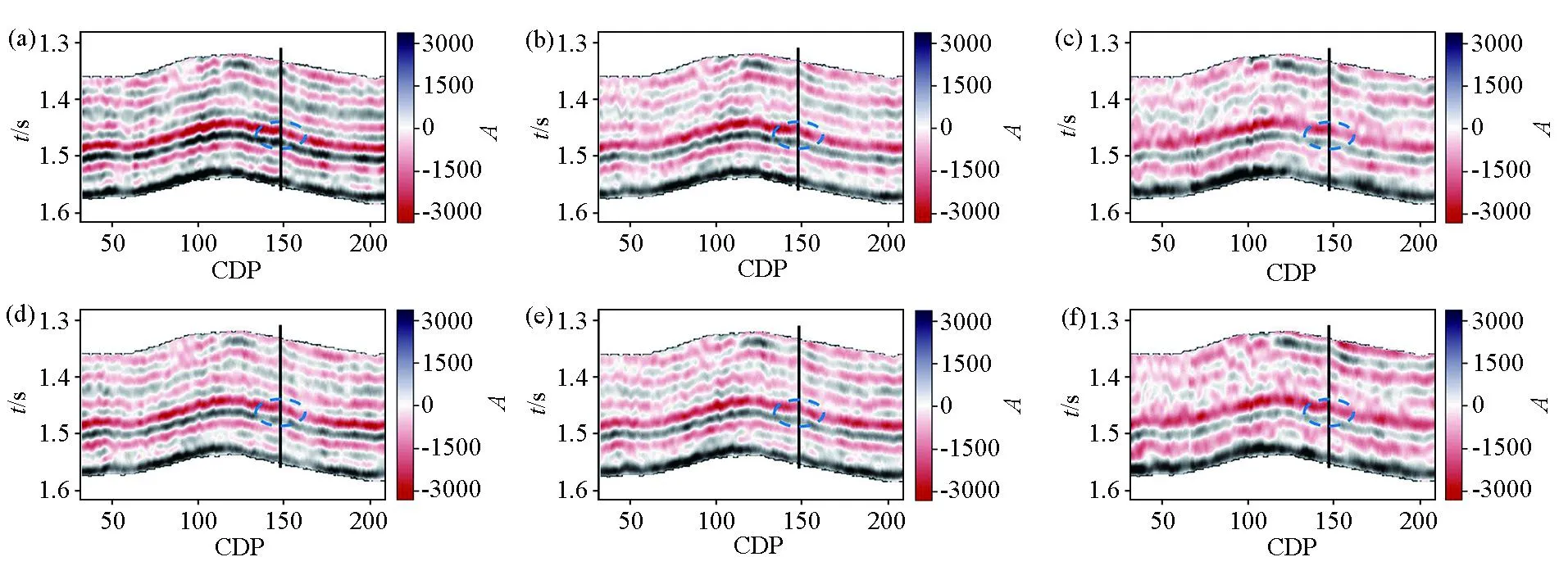
a—入射角6°、方位角45°;b—入射角18°、方位角45°;c—入射角30°、方位角45°;d—入射角6°、方位角135°;e—入射角18°、方位角135°;f—入射角30°、方位角135°

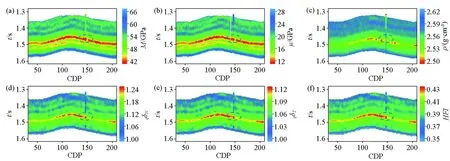
图7 纵波模量(a)、剪切模量(b)、密度(c)、准裂缝法向弱度(d)、准裂缝切向弱度(e)以及流体指示因子HFI(f)的反演结果Fig.7 Inversion results of P-wave modulus(a),shear modulus(b),density(c),normal weakness of quasi-fracture(d), tangential weakness of quasi-fracture(e),and fluid indicator factor HFI(f)

4 结论

随着油气勘探开发技术的进步,非常规资源勘探前景优越,裂缝型储层作为重点开发对象受到广泛关注。如何构建一个合理的流体因子,以精确识别裂缝性储层缝隙流体至关重要,本文对此做出一定的研究与深入,结论总结如下:

1)定义了新的缝隙流体指示因子,推导了包含缝隙流体因子的各向异性反射系数近似方程,在入射角为0°～30°范围内与P-K方程吻合较好。

2)应用改进的全局自适应MCMC反演算法反演,虽然效率上有一定提升,但仍有很大的优化空间。

3)成像测井解释结果表明目的层发育有大量裂缝,且钻井结果表明目的层钻遇油气,与反演结果认识相同,验证了本文提出的缝隙流体指示因子能够有效指示储层流体分布情况以及本文所提出的反演方法的准确性以及适用性。